基于最小熵反褶积的行星齿轮箱故障诊断

王 轩，徐九南，姜 毅，王细洋

（1.南昌航空大学 飞行器工程学院，南昌 330063；2.南昌工学院 机械与车辆工程学院，南昌 330108）

基于最小熵反褶积的行星齿轮箱故障诊断

王 轩1，徐九南2，姜 毅2，王细洋1

（1.南昌航空大学 飞行器工程学院，南昌 330063；2.南昌工学院 机械与车辆工程学院，南昌 330108）

行星齿轮箱具有传动比大、传动效率高等优点，但比定轴齿轮有更复杂的结构，因常工作在恶劣的条件下，容易出现磨损或疲劳裂纹等故障。扭振信号因信噪比高、频谱结构简单等优点有利于对行星齿轮箱的故障诊断。所以针对重载、强噪声环境下行星齿轮箱故障特征的提取，提出了基于最小熵反褶积（Minimum entropy deconvolution, MED）的扭振信号时域分析方法，该方法通过反转滤波加强冲击特性从而提取行星轮的故障特征。通过对仿真信号和行星齿轮箱的扭振信号分析，在时域上提取了明显的故障冲击特征，并且较频谱分析能更直观清晰地看出故障特性。通过对不同负载情况下的比较，发现该方法对处于大负载情况下的故障诊断效果更佳。

行星齿轮箱；扭振信号；最小熵反褶积；故障特征

0 引言

行星齿轮箱具有体积小、重量轻、传动比大、传动效率高与承载能力强等等诸多优点，在诸如航空、船舶、矿山和风力发电等工程机械中有广泛的应用。行星齿轮箱通常在恶劣环境下工作，例如重载、高速、高降速比、非封闭性，容易发生齿根裂纹、轮齿疲劳点蚀乃至轮齿或轴断裂等失效情况。相比横向振动信号，扭振信号从故障激励到传感器间的传递途径要简单很多，不容易受其他振源的影响，所以扭振信号的信噪比高，频谱成分比横向振动信号更加简单。行星齿轮啮合位置会随时间变化[1]，但不会对扭振信号产生额外的调制作用，扭振信号对故障更加敏感[2]。利用扭振信号更容易发现齿轮的点灼、胶合、齿根疲劳裂纹、局部断齿等早期故障。

针对旋转机械故障特征的提取，最小熵反褶积是一种很有效的方法，国内外学者也有一定的研究。Endo和Randall[3]在2007年首次将MED应用到齿轮故障诊断中，并提出基于MED的增强自回归模型对齿轮轮齿进行故障诊断；Geoff L.McDonald等[4]改进了MED算法，利用最大相关峰态反褶积对齿轮轮齿进行故障诊断；王志坚，韩振南等[5]基于最小熵反褶积和总体平均经验模态分解方法对强噪声下滚动轴承微弱故障特征进行了有效的提取；N.Sawalhi等[6]将MED与谱峭度结合加强了对滚动轴承故障特征提取；Dan He等[7]基于MED与谱峭度对多重故障的旋转机械进行准确诊断。但是以上都是对横向振动信号进行分析，没有针对行星齿轮箱扭振信号进行研究。冯志鹏、褚福磊等[8]对行星齿轮箱扭振信号进行解调并且分析诊断故障，但从频谱上看故障特征不明显；徐洪志[9]总结了傅立叶频谱分析和基于AR模型的功率谱估计的扭振分析方法，但是没有给出实际的分析例子。

本文研究基于最小熵反褶积的扭振时域分析方法，在时域上对以角速度形式表示的扭振信号进行分析，以提取行星齿轮箱的故障特性。

1 最小熵反褶积原理

Wiggins[10]在1978年提出最小熵反褶积并应用于地震检测。信息熵作为一个量度，是度量不确定性的一个指标。当信息熵越大，设备的可维修性就越差，不确定性越大。当处理后的信号由大的脉冲组合时，它的熵为最小，MED就是通过对有限脉冲响应（Finite impulse response，FIR）滤波器系数迭代地选择，对信号反转滤波突出少数大的脉冲，再根据最大峭度值来作为迭代终止条件[3]。所以MED对齿轮等旋转机械的故障特征提取非常适用。

假设某一齿轮有故障时的信号为：

y(n)为输出信号，x(n)为故障冲击序列，s(n)信号中的未知输入序列，e(n)为噪声。

解反褶积的问题就是通过FIR滤波器f对输出信号y(n)反转滤波提取出故障冲击x(n)：

当齿轮发生故障时，x(n)的冲击成分加强、峭度值增大，相对的s(n)和e(n)的冲击成分较弱、峭度值偏小。所以希望通过反转滤波后的效果为：f*x(n)≈x(n)，f*s(n)→0，f*e(n)→0。

Endo等[3]归纳了MED具体过程：

1）利用最小熵算法找到长度为L的FIR滤波器f最优系数，优化输出信号h(n)峭度：

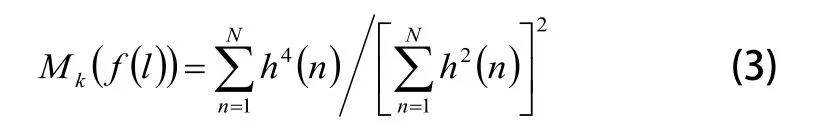
2）反转滤波器卷积计算公式：

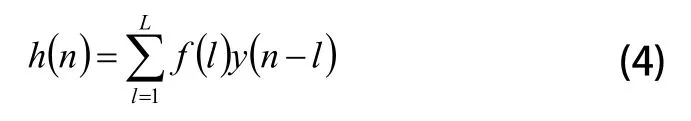
3）当目标函数式(3)出现最优解时（峭度值最大），即：

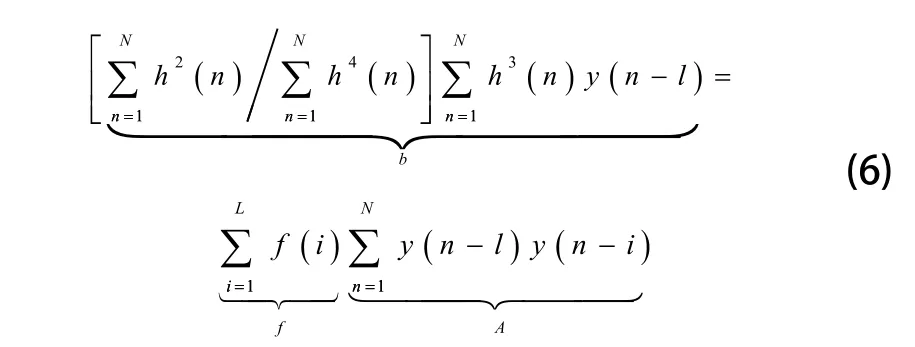
可将上式写成：

式中b是滤波器的输入信号和输入信号的互相关，A是输出信号h(n)的自相关矩阵，f是反转滤波器系数，所以f=A−1b。

由以上可知MED算法步骤如下所示：

1）初始化f(0)中元素全为1；

2）根据式(4)，通过y(0)和f(0)计算h(0)；

3）根据式(7)，通过y(0)和h(0)计算b(1)；

4）计算f(1)=A(-1)b(1)；

5）设定误差阀值。若误差小于阀值，停止递归。否则，返回步骤3）。

2 仿真分析

为了验证MED方法对行星齿轮箱故障诊断的有效性，对行星齿轮箱故障扭转振动的仿真信号进行分析，仿真信号[11]如下所示：

A为调幅函数，B为调频函数，N(t)为强度为25dBW的高斯白噪声，为相位值。

其中fs-c、fp-c、fr-c、fm、fg分别为太阳轮相对于行星架的旋转频率、行星轮相对于行星架的旋转频率、齿圈相对于行星架的旋转频率、啮合频率和故障齿轮的故障频率。由公式可得：

其中zs、zp、zr为太阳轮、行星轮和齿圈的齿数。

表1为模拟构造的行星齿轮箱的参数。采样频率fs为10000Hz，采样时间为1s，以太阳轮为输入轴，转速为1430r/min。

扭振信号较横向振动信号在行星齿轮故障诊断方面有一定优势，但行星齿轮箱比其他旋转设备结构更加复杂，如式(8)、式(9)所示，即使不考虑噪声的影响，除了故障频率fg外，还有fs-c、fp-c、fr-c、fm等成分。图1、图2分别为仿真信号的时域波形和经MED方法处理后的时域波形。从图2可看出，经过MED方法处理后的时域信号有几个明显的大的脉冲，并且周期为T，取某一个周期的两个端点t1=0.2651s和t2=0.4517s，T=0.1866s，所以f=1/T=5.36Hz。经计算行星轮[12]的故障频率fg=5.36Hz，从而判断行星轮出现了故障。通过对仿真信号的分析，说明了MED方法能在众多冲击成分中准确有效的提取故障冲击脉冲。

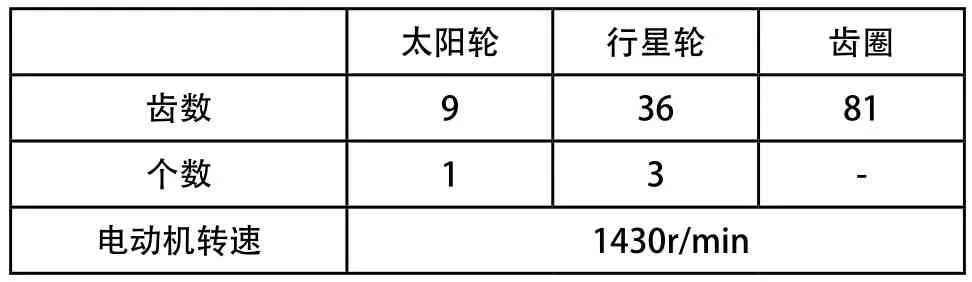
表1 模拟构造行星齿轮箱参数

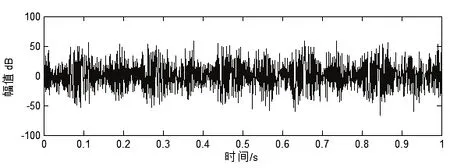
图1 仿真信号时域波形

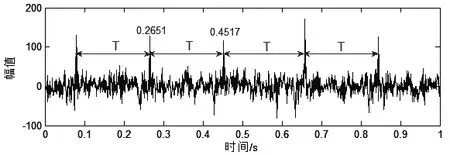
图2 经MED处理后的仿真信号时域波形

3 齿轮故障扭振信号分析

3.1 齿轮扭振实验系统

实验所用的行星齿轮箱为PXDS115-4型单级传动行星齿轮箱，行星齿轮箱相关的设备参数和运行参数如表2、表3所示。

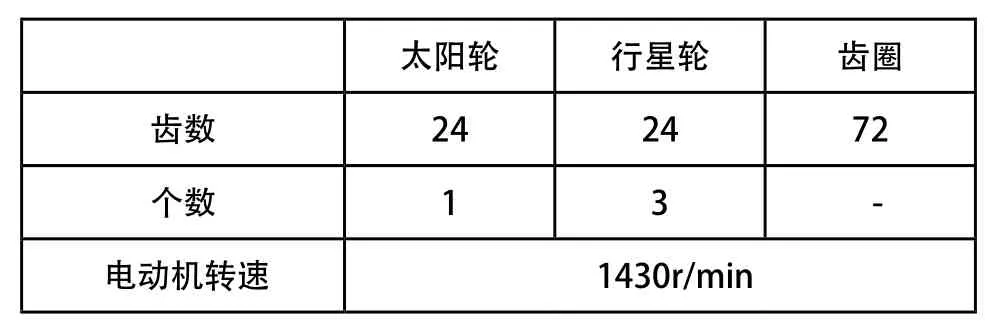
表2 行星齿轮箱设备参数

表3 行星齿轮箱相关运行参数

根据相关公式计算[12]，太阳轮局部故障频率fs=53.63Hz，行星轮局部故障频率fp=17.875Hz。为了采集齿轮箱故障下的扭振信号，以人为破坏的方式对其中一个行星轮进行破坏，然后采用如图3所示的实验平台采集行星齿轮箱扭振信号。

实验台系统运行后将数据采集卡与增量式编码器相联，利用线性插值重采样的方法对角域信号重构，这样就得到了以角速度形式的扭振信号。

图3 实验平台

3.2 小负载情况下的扭振信号分析

先对小负载工作状况下采集信号，如图4所示，虽然系统没有增加额外负载，但也并不能看出故障特性。然后利用最小熵反褶积方法对信号处理，结果如图5所示。

图4 小负载扭振信号

图5 MED处理后的小负载信号

从图5可看出，经过MED方法处理后的信号中有以T为周期出现的大的脉冲，说明从信号提取了比较大的冲击信号。其中T=0.2507-0.1946=0.0561s，fs=1/T=17.83Hz，与行星轮的故障频率fp相同，说明了行星轮出现了故障，与实际情况相同。但也可从图中看出经MED方法提取的故障冲击成分幅值较其他成分并没有大多少，有的甚至都没有凸显出来，这种情况与实验台采集行星齿轮箱扭振信号的特殊性有关。因为编码器安装在行星齿轮箱的输入轴（太阳轮），采集的信号是以输入轴角速度形式的扭振信号，所以输入轴信号对以啮合频率为载波信号的调制作用较强。当只有自身负载（小负载）时，故障信号和输入轴信号都有较强调制作用，所以经MED处理后出现以上结果。

3.3 大负载情况下的扭振信号分析

行星齿轮箱通常在恶劣环境下工作，例如重载、高速、高降速比，为了更加接近行星齿轮箱实际工作状态，可通过磁粉制动器调节扭矩大小，增大负载。图6为扭矩为20N·m时MED处理前后对比情况。

从图6可看出，经MED方法处理的信号中有特别明显的以T为周期的大的脉冲，说明从信号中提取了大的冲击信号。其中T=0.2194-0.1624=0.057s，f=1/T=17.54Hz（因加了负载，测得的转速比理论值小，所以频率也不同，下同），与行星轮的故障频率fp相同，说明行星轮出现了故障，与实际情况符合。磁粉制动器增大的负载通过行星齿轮箱的输出轴传递到行星齿轮箱内，因为负载的作用，当故障齿轮与太阳轮或者齿圈啮合时，振动冲击会更加强烈。虽然负载增大其他成分的冲击程度也会增大，但对故障齿轮的冲击特性影响最大，从处理后提取突出的故障信号的脉冲也可看出这点。与只有自身负载（小负载）相比，增大了负载后虽然系统振动幅度更大、噪声更多，但利用MED方法对故障特性的提取更加有效，从而能很好的诊断设备故障。

图6 负载20N·m时MED处理前后对比

为了验证MED方法对系统增加大负载后故障诊断的可效性，通过磁粉制动器分别增大负载到30N·m 、40N·m 、50N·m，图7、图8、图9为30N·m 、40N·m 、50N·m时MED前后对比情况。与负载为20N·m时相似，经过MED方法处理后的信号中都出现了以T为周期的大的脉冲，表4为各种扭矩下计算的周期T和频率f，皆与故障频率fp相同。

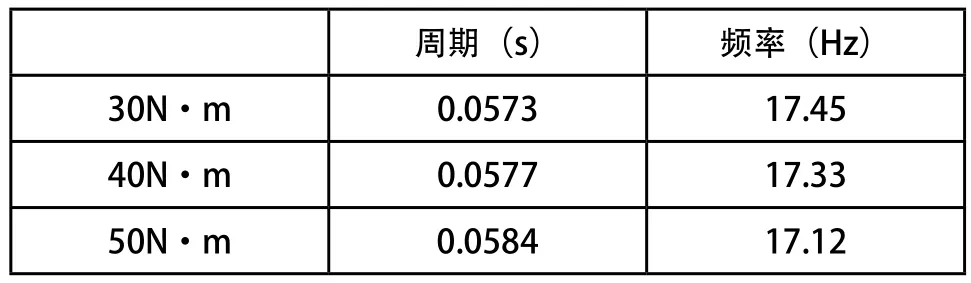
表4 各扭矩下的T和f

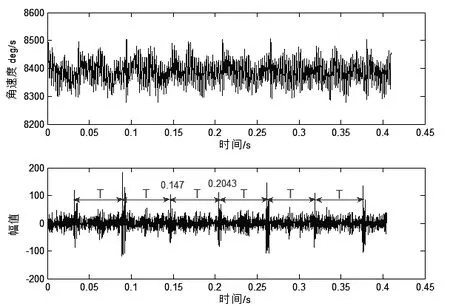
图7 负载30N·m时MED处理前后对

图8 负载40N·m时MED处理前后比

图9 负载50N·m时MED处理前后比

峭度指标是无量纲参数，对冲击信号很敏感，特别适用于诊断齿轮表面损伤类故障。峭度值越大表明信号中所含冲击成分越重。表5为几种情况下峭度值对比。可看出当增加的负载越大时，峭度值越大、比例关系越大，说明MED方法对处于大负载情况下的行星齿轮箱的故障诊断效果更佳。

表5 峭度值对比

扭振信号较横向振动信号有信噪比高，频谱结构简单等优点，而且行星齿轮啮合位置的时变不会对扭振信号产生额外的调制作用，扭振信号对故障更加敏感，但在重载、强噪声的情况下故障特性仍会被“埋没”。图10为负载20N·m时的频谱图。因为负载的增大，只有太阳轮转频fs幅值明显，故障频率fp在频率图中被淹没。在啮合频率（fm、2fm）周围虽然有边频带，但幅值都不大，故障频率fp并没有凸显出来。所以较扭振信号的频谱分析，经MED方法处理后的时域信号更能直观清晰地看出故障特性。

综上，扭振信号结构简单，在为数不多的冲击成分中，齿轮发生故障时所产生的冲击脉冲较其他成分的冲击脉冲更大、更加明显，因此基于MED的扭振时域分析可更好地提取故障冲击特征，从而检测设备故障。

4 结论

1）针对行星齿轮箱故障冲击特征的提取，提出了基于最小熵反褶积的扭振时域分析方法。

2）由于实验系统和扭振信号的特殊性，在小负载情况下MED方法对故障冲击特征提取的效果不是很好。

3）通过对仿真信号和大负载情况下行星齿轮箱扭振信号的分析，发现MED方法能很有效的提取故障冲击特征。

4）通过对不同负载情况下峭度值的对比，发现MED方法对处于大负载情况下的行星齿轮箱的故障诊断效果更佳。

5）与频谱分析相比，经MED处理后能直观清晰地观察到在时域信号上的故障冲击脉冲，更有效的对行星齿轮箱进行故障诊断。

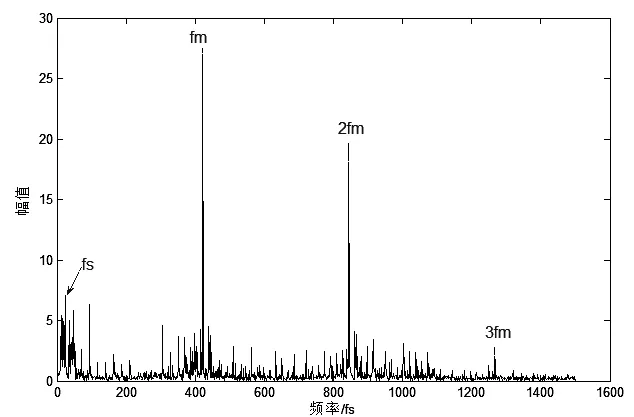
图10 负载20N·m时频谱图

[1] 雷亚国,汤伟,孔德同,等.基于传动机理分析的行星齿轮箱振动信号仿真及其故障诊断[J].机械工程学报,2014,50(17):61-68.

[2] 丁康,李巍华,朱小勇.齿轮及齿轮箱故障诊断实用技术[M].北京:机械工业出版社,2005.

[3] Endo H, Randall R B. Enhancement of autoregressive model based gear tooth fault detection technique by the use of minimum entropy deconvolution filter[J].Mechanical Systems & Signal Processing,2007,21(2):906-919.

[4] Geoff L.McDonald, Qing Zhao, Ming J.Zuo,Maximum correlated Kurtosis deconvolution and application on gear tooth chip fault detection[J].Mechanical Systems and Signal Processing,2012,33(6):273-255.

[5] 王志坚,韩振南,等.基于MED-EEMD的滚动轴承微弱故障特征提取[J].农机工程学报,2014,30(23):70-78.

[6] N. Sawalhi, R. Randall, H. Endo,The enhancement of fault detection and diagnosis in rolling element bearings using minimum entropy deconvolution combined with spectral kurtosis[J].Mech.Syst. Signal Process.2007,21(6):2616-2633.

[7] Dan He,Xiufeng Wang. Identification of multiple faults in rotating machinery based on minimum entropy deconvolution combined with spectral kurtosis[J].Mechanical Systems and Signal Processing,2016,81(3):235-249.

[8] 冯志鹏,褚福磊.行星齿轮箱故障诊断的扭转振动信号分析方法[J].中国电机工程学报,2013,33(14):101-106.

[9] 徐洪志.旋转机械轴系扭振测量研究[D].北京:清华大学,2005.

[10] R.A.Wiggins, Minimum entropy deconvolution[J].Geoexploration,1978,16(1):21-35.

[11] Zhipeng Feng,Ming J.Zuo. Fault diagnosis of planetary gearboxes via torsional vibration signalanalysis[J].Mechanical Systems and Signal Processing,2013(2),36:401-421.

[12] 冯志鹏,赵镭镭,褚福磊.行星齿轮箱局部故障振动频谱结构[J].中国电机工程学报,2013,33(5):119-127.

Fault diagnosis of planetary gearboxes based on minimum entropy deconvolution

WANG Xuan1, XU Jiu-nan2, JIANG Yi2, WANG Xi-yang1

TP206

：A

1009-0134(2017)07-0001-05

2017-03-18

国家自然科学基金资助项目（51465040）

王轩（1992 -），男，湖北人，硕士研究生，研究方向为机械设备监控与故障诊断。