几种实正规矩阵的性质
张建刚,申 冉
1.上海师范大学数学系,上海,200234;2.东华大学理学院,上海,201620
几种实正规矩阵的性质
张建刚1,申 冉2
1.上海师范大学数学系,上海,200234;2.东华大学理学院,上海,201620
有针对性地研究了几种实正规矩阵的部分性质,特别是针对特征值和对角化等方面,得到它们的联系和区别之处。给出了实正规矩阵(正交矩阵)是实对称阵(正定矩阵)的充要条件,同时研究了可逆矩阵关于实正规矩阵的分解性质。
正规矩阵;正交矩阵;对称矩阵;正定矩阵
1 问题提出
正规矩阵是矩阵理论的主要研究对象之一。 正交矩阵、实对称(反对称)矩阵以及正定矩阵都是实的正规矩阵。本文通过有针对性地研究这几类实的正规矩阵的部分性质,特别是针对特征值和对角化等方面,得到它们的联系和区别之处。
如无特别说明,本文所讨论的矩阵都是实数域上的矩阵。实数域上所有n阶方阵的集合记作Mn(R),对任意的A∈Mn(R),AT表示转置矩阵,A*表示伴随矩阵,A-1表示逆矩阵(如果存在),En表示n阶单位阵。
文中所涉及到的其他术语,参见文献[1]。
2 几种正规矩阵的性质比较
定义2.1如果A∈Mn(R),满足AAT=ATA=En,即AT=A-1,则称A为正交矩阵[1]298-343。
正交矩阵具有以下性质:
(1)正交矩阵的乘积和正交矩阵的逆矩阵都是正交矩阵。两个正交矩阵的和未必正交,如令A=E2,B=-E2,则有A+B不是正交矩阵。
(2)正交矩阵的特征值的模等于1,其实的特征值只能为1或-1。
(3)上(下)三角正交矩阵必为对角矩阵,且对角线上的元素只能为1或-1。
定义2.2设A∈Mn(R)且A可逆,则A可以分解为A=QR,其中,Q为正交矩阵,R是一个对角线上全为正数的上三角矩阵,并且这种分解形式是唯一的(上述分解称为正交三角分解)。
上述分解形式,在研究可逆矩阵的性质时是非常有帮助的。
定义2.3如果A∈Mn(R),且满足A=AT,即对任意的i=1,2,…,n;j=1,2,…n,都有aij=aji,则称A为对称矩阵[1]298-343。
对称矩阵的性质:
(1)两个对称矩阵的和还是对称矩阵。两个对称矩阵A,B的乘积AB仍是对称矩阵的充要条件是AB=BA。
(2)实对称矩阵的特征值都是实数,且属于不同特征值的特征向量正交。
(3)若A∈Mn(R)为对称阵,则存在正交阵Q,使得QTAQ为对角矩阵,且对角线上元素为A的全部特征值(称为实对称阵的正交对角化)。
由正交阵的定义可知,n阶实矩阵A是正交阵当且仅当AAT=En。对于对称阵,有下面的结论。
命题2.4设A∈Mn(R),则A是对称阵当且仅当AAT=A2。
证明必要性是显然的。下证充分性,首先注意到下面的事实,若B∈Mn(R),则:
B=0⟺BBT=0⟺tr(BBT)=0
另一方面,由条件AAT=A2,有:
tr((A-AT)(A-AT)T)
=tr((A-AT)(AT-A))
=tr(ATA-(AT)2)
=tr(AT(A-AT))
=tr((A-AT)AT)
=tr(AAT-(A2)T)
=tr(AAT)-tr(A2)=0
因此,A-AT=0,即A=AT,A是对称阵。
由上述命题,容易得到下面正交矩阵和对称矩阵之间的关系。
命题2.5设A∈Mn(R),则下列三个条件中任意两个成立,则另一个也成立。
(1)A是一个对称矩阵。
(2)A是一个正交矩阵。
(3)A2=En(以下称满足此条件的矩阵为对合阵)。
例子2.6设A∈Mn(R),且A是对称矩阵, 若A也是对合阵。证明存在正交矩阵Q,使得:
证明由对称矩阵的性质(3),存在正交阵Q,使得QTAQ为对角矩阵,且对角线上元素为A的全部特征值。另一方面,设A的特征值为λ,对应的特征向量为α,则有Aα=λα。结合条件A2=En,容易看到λ2=1,从而A的特征值为1或者-1,所以结论成立。
矩阵A∈Mn(R)可以对角化,当且仅当A的特征值都是实数,且A的所有特征值对应的特征子空间的维数之和等于n。而正交阵的特征值不一定是实数,所以不是所有的正交矩阵都能对角化。但有下面的结论:
命题2.7设A∈Mn(R),且A为正交矩阵,则A的特征值都是实数,当且仅当A是对称阵。
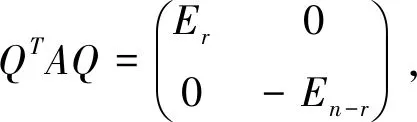
由上述结论可知,一般的正交阵未必可以对角化,但如果特征值都是实数,则可以实现对角化。
推论2.8设A∈Mn(R),且A为正交矩阵,若A的特征值都是实数,则:
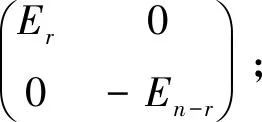
(2)rank(A+En)+rank(A-En)=n。
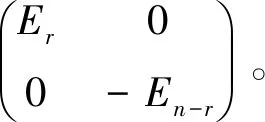
(2)若A的特征值为1,则由(1)可知,A=En。同理,若A的特征值为-1,A=-En。若1,-1都是A的特征值,由于A可以对角化,故dimV1+dimV-1=n,其中V1,V-1分别是1,-1对应的特征子空间。又因为
dimV1=n-rank(En-A)
=n-rank(A-En)
dimV-1=n-rank(-En-A)
=n-rank(A+En)
故得证。
由命题2.5和2.7容易得到下面的结论。
推论2.9设A∈Mn(R),且A为正交矩阵,则下列命题等价:
(1)A的特征值都是实数。
(2)A是对称阵。
(3)A为对合阵。
定义2.10设A∈Mn(R),且A=AT,如果二次型XTAX是正定的,其中X为n维列向量,则称A为正定矩阵。
正定矩阵的基本性质:
(1)设A,B∈Mn(R),m∈Z,k是正实数,若A,B都正定,则A-1,A*,Am,A+B,kA都正定。
(2)实对称阵A是正定矩阵,当且仅当A的特征值都大于零。
(3)实矩阵A是正定矩阵,当且仅当A合同于单位矩阵(即存在实可逆阵C,满足A=CTC);当且仅当A正交相似于一个对角阵,且对角线上为其全部(正的)特征值。
命题2.11实(对称)矩阵A是正定矩阵当且仅当存在可逆上三角矩阵R,满足A=RTR。
证明充分性由正定矩阵的基本性质(3)易得,下证必要性。由正定矩阵的基本性质(3),存在可逆阵C, 使得A=CTC;另一方面,由引理2.2,C可以分解为C=QR,其中Q为正交矩阵,R是一个对角线上全为正数的上三角矩阵,则A=(QR)TQR=RTQTQR=RTR。
命题2.12正交矩阵A是正定矩阵,当且仅当A是单位阵。
证明充分性是显然的,下证必要性。若正交矩阵A是正定矩阵,则A必为实对称阵,由命题2.5和例子2.6的证明可知,A的特征值只能为1或者-1。又因为正定矩阵的特征值都大于0,故A的特征值只能为1,由正定矩阵的基本性质(3)易得,A正交相似于单位阵,所以A是单位阵。
关于正定矩阵乘积的正定性,有着类似于实对称矩阵乘积的对称性的结论。
命题2.13两个正定矩阵A,B的乘积是正定矩阵的充要条件AB=BA。特别的,正定矩阵的方幂是正定的。
证明必要性为显然。这是因为正定阵一定是对称阵,所以如果A,B的乘积是正定矩阵,则AB必为对称阵,由对称阵的基本性质(1),AB=BA。
下证充分性。首先由对称阵的基本性质,若AB=BA,则AB是对称阵。因为A,B都是正定矩阵,由正定矩阵的基本性质(3),分别存在实的可逆阵P,Q,使得A=PTP,B=QTQ,则AB=PTPQTQ。进一步,容易看到:
QABQ-1=QPTPQTQQ-1
=QPTPQT=(PQT)TPQT
由正定阵的基本性质,(PQT)TPQT是一个正定阵,所以上式说明AB与一个正定矩阵相似,故AB的特征值都是正数,所以AB也是正定阵。
命题2.14设A是实对称矩阵,则A正定,当且仅当存在唯一的正定矩阵B,满足A=B2。
证明充分性由命题2.13为显然,下面证明必要性。由正定矩阵的正交相似性,存在正交阵U,使得:
UTAU=diag(λ1,λ2,…,λn)
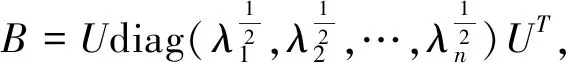


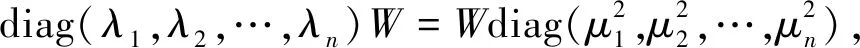
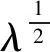
即B=C。
推论2.15设A∈Mn(R)且A可逆,则A可以分解为一个正交阵和一个正定阵之积,也可以分解为一个正定阵与一个正交阵之积。特别地,若A正交,则分解形式唯一。
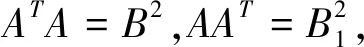
A=(AT)-1B2=(AT)-1BB
分别记(AT)-1B=P,B1(AT)-1=Q,则A=PB,A=B1Q,下证P,Q分别为正交矩阵。事实上:
PPT=(AT)-1B(AT)-1(B)T
=(AT)-1BBTA-1=(AT)-1B2A-1
=(AT)-1ATAA-1=En
QTQ=(B1(AT)-1)TB1(AT)-1
=A-1AAT(AT)-1=En
故结论成立。特别地,若A正交,设A=PB,其中P是正交阵,B是正定阵,则有P-1A=B。由于P-1A正交而B正定,由命题2.12,B=En。类似的可以证明另一种分解形式也是唯一的。
定义2.16如果A∈Mn(R),满足AAT=ATA,则称A为(实)正规矩阵。
不难看到,上述所讨论的正交矩阵,对称(反对称)矩阵和正定矩阵都是正规矩阵。
正规矩阵的基本性质:
(1)设A∈Mn(R)是正规矩阵,m∈N,k是任意实数,则AT,Am,kA均是正规矩阵,且A可逆时,A-1,A*也都是正规矩阵。
(2)设A∈Mn(R)是正规矩阵,若A是上三角阵,则A必为对角矩阵。
命题2.17设A∈Mn(R),且A是正规矩阵,则A的特征值都是实数,当且仅当A是对称阵。特别地,若特征值都是正实数,当且仅当A是正定矩阵。
证明充分性是显然的,只需证明必要性。下面利用数学归纳法加以证明。首先,当n=1时,结论显然成立。假设结论对n-1阶矩阵成立,即对任意n-1阶的实正规阵,如果特征值都是实数,则它是对称阵。下面考虑阶数为n的情形。
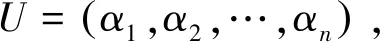
其中,α是n-1维实的行向量,B是一个n-1阶实矩阵。记UTAU=C,则CCT=CTC。事实上,因为AAT=ATA,CCT=(UTAU)(UTATU)=UTAATU=UTATAU=(UTATU)(UTAU)=CTC,即有:
特别地,由正定矩阵的基本性质,若A的特征值都是正实数,当且仅当它是正定矩阵。
推论2.18设A∈Mn(R),且A为正规矩阵,若A的特征值都是实数,则A可以相似对角化。
[1]张禾瑞,郝炳新.高等代数[M].北京:高等教育出版社,2007
[2]杨子胥.高等代数习题集:上[M].济南:山东科学技术出版社,2000:542-562
[3]杨子胥.高等代数习题集:下[M].济南:山东科学技术出版社,2001:390-451
[4]陈祥恩,程辉,乔虎生,等.高等代数专题选讲[M].北京:中国科学技术出版社,2013:182-201
[5]张建刚,申冉.线性流形的性质[J].大学数学,2015,31(4):90-94
(责任编辑:汪材印)
10.3969/j.issn.1673-2006.2017.05.027
2016-12-20
国家自然科学基金“某些完全正则半群的性质和结构”(11201305)。
张建刚(1977-),山东禹城人,博士,副教授,研究方向:代数半群理论。
O151.2
:A
:1673-2006(2017)05-0094-04

