基于Maxwell与Simplorer仿真分析磁通门磁场传感器瞬态响应*

叶魏涛,朱万华,张 乐,方广有

(1.中国科学院电子学研究所电磁辐射与探测技术重点实验室,北京 100190;2.中国科学院大学,北京 100190)



基于Maxwell与Simplorer仿真分析磁通门磁场传感器瞬态响应*

叶魏涛1,2,朱万华1*,张 乐1,方广有1

(1.中国科学院电子学研究所电磁辐射与探测技术重点实验室,北京 100190;2.中国科学院大学,北京 100190)

为分析磁通门磁场传感器的工作原理,基于Maxwell和Simplorer软件建立了磁通门磁场传感器的电磁联合仿真模型,仿真了磁通门非线性激励电路中电流波形和磁通门传感器的瞬态响应过程,分析计算了磁通门二次谐波灵敏度以及磁通门传感器的转换系数。为验证仿真模型的准确性,利用钴基非晶薄片制作了磁通门传感器探头并利用开关电源驱动电路激励磁通门工作。实际测量的激励电流波形与仿真结果基本一致,磁通门二次谐波灵敏度的测量值与仿真值误差小于1.1%。测量磁通门的频率响应曲线得到磁通门的转换系数为100 mV/μT,与仿真值几乎完全一致,两者误差小于1.5%。该仿真模型对理解磁通门传感器的工作原理、瞬态响应过程以及指导微型磁通门传感器设计具有重要意义。

磁通门传感器,瞬态响应,联合仿真,灵敏度

磁通门磁场传感器是一种测量直流磁场和低频交流磁场的矢量传感器。尽管磁通门磁场传感器最早出现在20世纪30年代[1-3],但它仍然广泛应用于地磁监测[4]、磁异常探测[5]、深空磁探测[6-7]等诸多领域,这主要归功于磁通门传感器具有出色的时间、温度稳定性,低噪声特性,较大的动态范围以及稳固的机械性能。近年来仍有许多学者致力于磁通门磁场传感器的微型化[8-9]和低功耗方面的研究[10-11]。出于制造磁通门传感器的工艺较复杂、成本较高等因素考虑,在制作磁通门之前能够建立模型进行仿真分析设计参数对磁通门性能参数影响显得尤为重要。

很多科研工作者对磁通门磁场传感器的工作原理作了研究,如Felch等人1947年首次利用多项式模型模拟磁化曲线解释了磁通门传感器的基本理论模型[12]。1965年Gordon等人使用折线模型拟合磁化曲线推导出磁通门灵敏度的近似公式,得出磁通门灵敏度与激励信号频率、次级线圈匝数、磁芯横截面积等成正比例的结论[13]。1972年Burger提出了分段线性模型拟合磁化曲线得出磁通门输出信号与磁芯材料动态磁导率的一阶微分成正比的结论[14]。2006年Geiler等人利用反正切函数模型拟合实际磁化曲线,分析了磁通门二次谐波灵敏度,误差仍然大于50%[15]。因为磁通门传感器是基于磁化曲线的非线性原理工作的,而且还依赖于激励电流波形,所以很难用一个简单的数学模型进行分析。

得益于计算机技术的发展,各种计算仿真软件技术革新,人们开始利用计算机仿真技术分析磁通门传感器。1997年Moldovanu等人首次使用SPICE模型仿真了磁通门传感器的动态响应,他们利用Jiles-Atherton模型拟合VACOPERM-100铁基非晶的磁化曲线,分析了不同外磁场情况下的次级线圈中的感应电动势变化[16]。之后Trujillo等人利用SPICE模型分析了磁芯材料不同磁化曲线特性对磁通门输出信号各次谐波成分的影响[17]。西北工业大学刘诗斌教授的小组也利用反正切函数拟合磁化曲线建立非线性电感模型,利用HSPICE模型分析了磁通门的二次谐波灵敏度[18-20]。因为磁化曲线都是通过利用函数拟合磁化曲线,且磁芯几何形状引起的退磁场的影响没有考虑到或者考虑不全面,所以利用SPICE模型仿真结果误差都相对较大。

在本文中,作者基于有限元仿真软件Maxwell建立了磁通门传感器探头的3D模型,基于电路仿真软件Simplorer建立了磁通门传感器的激励电路、信号处理电路。将磁材料的磁化曲线直接导入材料属性中,利用Maxwell软件和Simplorer软件进行了磁路、电路多物理域联合仿真,分析了磁通门传感器的二次谐波灵敏度(sensitivity)、磁通门传感器的转换系数(scaling factor)等,并制作了磁通门原理样机进行实验验证。仿真结果中的激励电流波形与实测电流波形完全重合,而且二次谐波灵敏度仿真结果与实际结果误差小于1.1%、转换系数仿真结果与实测结果误差小于1.5%。实验证明该仿真模型是准确有效的,是理解和分析磁通门磁场传感器具有重要手段,对于指导微型化磁通门传感器设计具有重要意义。

1 磁通门磁场传感器基本原理

磁通门传感器基本结构如图1所示,它包含两个几何尺寸一致的铁磁材料(长l,宽w,高h),铁磁材料上分别绕有n1匝漆包线作为激励线圈,在激励线圈外缠绕n2匝漆包线作为感应线圈(在某些结构中也可同时作为补偿线圈)。通常感应线圈长度等于或略大于激励线圈长度。

图1 磁通门传感器探头原理图

在激励线圈中通入频率为fexc的交变电流Iexc(t),从而在激励线圈中产生频率为fexc的激励磁场Hexc(t),该激励磁场将铁磁材料周期性的磁化至饱和。磁通门探头放置在磁场强度为Hex的均匀磁场中,铁磁材料的磁化曲线如图2所示。

图2 铁磁材料典型磁化曲线

定义铁磁材料的有效磁导率为μapp(t),则

B(t)=μ0μapp(t)H(t)

(1)

在某时刻t磁芯a和磁芯b磁化状态分别如图2所示(b和d关于原点中心对称),从而在次级线圈中的磁通密度为

Br(t)=μ0μappa(t)[Hexc(t)+Hex]+
μ0μappb(t)[-Hexc(t)+Hex]

(2)

因为磁化曲线是中心对称的,所以μapp(t)的变化频率为2fexc,并且μappb(t)=μappd(t)=μapp(t)。而且,激励磁场幅度远远大于被测磁场幅度,根据柯西中值定理可得

Br(t)=2μ0μappc(t)Hex

(3)

根据法拉第电磁感应定律,感应线圈两端的感应电动势为

esen(t)=-2n2whμ0Hexdμapp(t)/dt

(4)

对μapp(t)进行傅里叶级数展开,则有

(5)

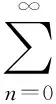
(6)

由式可知磁通门输出信号中只包含有激励信号的偶次谐波而且输出信号各次谐波与被测磁场成正比,比例系数与磁性横截面积、次级线圈匝数、铁磁材料的有效磁导率以及激励信号频率成正比。

磁通门次级线圈中输出信号经过模拟开关,输出信号中的偶次谐波被解调并经过低通滤波器和积分器,积分器输出信号Vo与外部被测磁场成正比,之后输出信号被反馈回路接到反馈线圈(在此结构中次级线圈被用作反馈线圈)产生反馈磁场抵消外部磁场,以增加磁通门传感器的线性度。

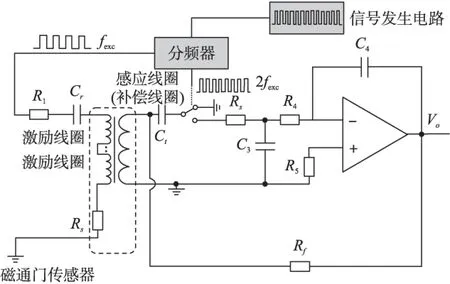
图3 磁通门传感器等效电路原理图

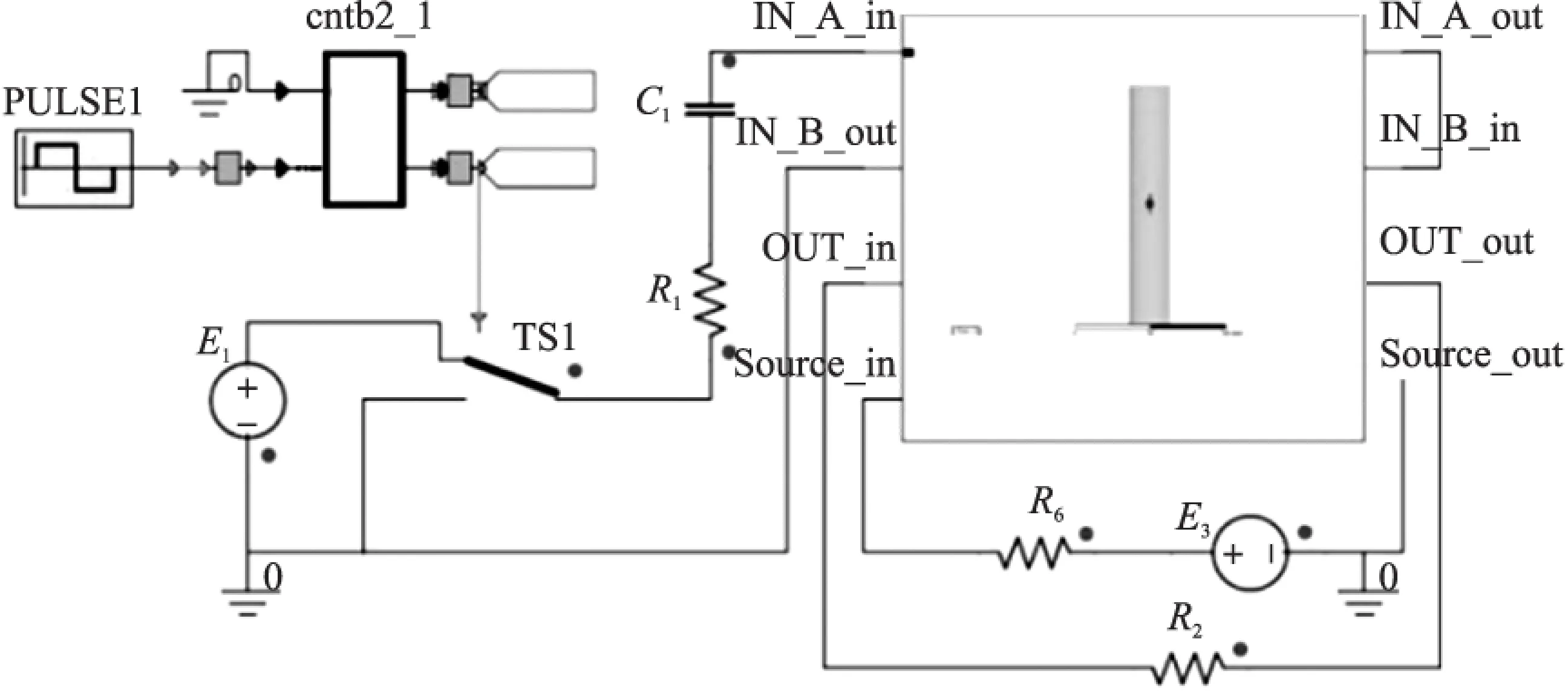
图5 磁通门传感器灵敏度仿真分析原理图

2 磁通门传感器电磁联合仿真

2.1 磁通门探头仿真模型

在Maxwell中设计磁通门探头如图4所示,两片几何尺寸相同(长30 mm,宽3 mm,厚25 μm)的钴基非晶薄带外绕有长30 mm的激励线圈,两非晶薄带间距1.25 mm,两初级线圈间隔0.135 mm。在激励线圈外绕有长度为30 mm,内径5 mm、外径5.4 mm的圆筒形次级线圈。为了提供稳定的均匀磁场信号,以磁通门所处位置为中心,构建长400 mm,内径40 mm,外径40.5 mm的长直螺线管,为测量提供均匀被测磁场。

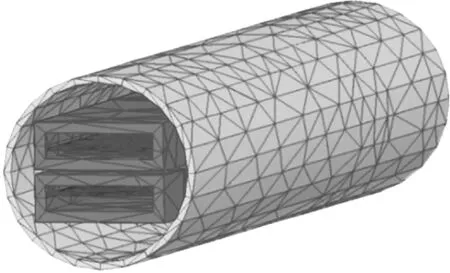
图4 磁通门传感器探头的磁场仿真模型

Maxwell求解类型选择瞬态分析,非晶材料的磁化曲线通过自建材料库导入实际材料的磁化曲线,激励线圈和次级线圈材料为铜线。激励线圈、次级线圈和螺线管均设置为外部信号激励,并且初级线圈绕线900匝,次级线圈绕线1 200匝,螺线管线圈绕线400匝。

2.2 磁通门传感器灵敏度仿真模型

通过将2.1节中建立的磁通门探头仿真模型以“子电路”形式导入Simplorer软件中,从而磁通门探头仿真模型在Simplorer中可等效为一个“集成电路”模块。磁仿真模型与通过“集成电路”管脚与磁通门探头激励电路、均匀磁场发生信号电路等互连,如图5所示。

直流电压源E1通过开关TS1周期性的断开、闭合,从而将磁通门探头中的非晶材料周期性的磁化至饱和状态。脉冲发生信号频率为31.25 kHz,经过D触发器频率实现二分频为15.625 kHz,所以实际磁通门激励信号频率为7.812 5 kHz。直流电源E1幅值为5 V,电阻R1阻值为66 Ω,电容C1容值为100 nF,电阻R6阻值为250 Ω,直流电源E3幅值根据不同外磁场设定不同幅值。

2.3 磁通门传感器瞬态响应仿真模型

通过将2.2节所建立的电磁仿真模型中的次级线圈输出信号通过电容耦合到模拟开关,控制模拟开关的信号频率是激励信号频率的2倍,即15.625 kHz。经过模拟开关解调后的信号经过低通滤波器和积分器滤波,然后将积分器输出信号经过一个阻值为5 kΩ的限流电阻反馈到次级线圈(作为反馈线圈)上,从而实现完整的磁通门传感器功能。此时磁场发生电路限流电阻R6阻值为500 Ω,电源E3根据不同被测磁场设定不同幅值。

图6 磁通门传感器瞬态响应仿真分析原理图

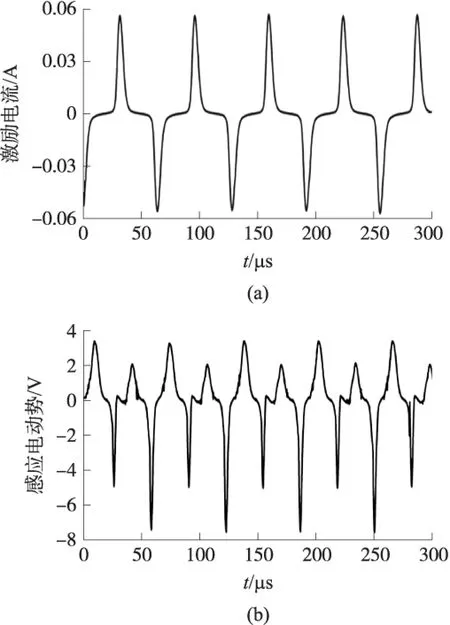
图7 磁通门传感器激励电流和感应电动势

3 磁通门传感器仿真结果分析

3.1 磁通门传感器二次谐波灵敏度

由2.1节可知螺线管的线圈常数为Ns=1 000 m-1,直流电源E3幅度为10 V时,经过螺线管内电流幅值为0.04 A,所以螺线管中心处磁感应强度为50.27 μT。磁通门传感器激励线圈内电流波形及次级线圈两端的感应电动势波形如图7所示,感应电动势最大值发生在激励电流曲率最大值处。因为电流曲率变化最大值处的磁芯磁导率变化也最大,根据式可知,磁导率变化越大,感应电动势也越大。

对感应线圈两端电动势信号作傅利叶变换得到其频谱如图8所示。

图8 磁通门感应电动势信号频谱

由图8可知,磁通门次级线圈两端的感应电动势中包含有激励信号的偶次谐波,而且二次谐波的幅值为0.914 2 V。磁通门灵敏度定义为感应电动势二次谐波幅度与被测磁场比值。故磁通门灵敏度为18 188 V/T。然后分别仿真电源E3幅度为5 V、2 V时磁通门传感器感应电动势输出,分析结果如表1所示。磁通门灵敏度都在18 000 V/T左右,具有高度的一致性。

表1 磁通门灵敏度仿真结果

3.2 磁通门传感器瞬态响应结果

当直流电源E3幅度为10 V时,限流电阻R6阻值为500 Ω,流经螺线管线圈的电流幅值为0.02 A,故而在螺线管中心位置产生的磁感应强度为25.13 μT。上电之,由于螺线管具有较大电感,所以上电后需要经过一小段时间后电流才能达到平稳状态(100 μs内)。磁通门传感器的输出电压如图9(a)所示,上电后输出电压接近饱和是因为正向通路放大倍数较大;随着反馈电流增加,磁通门传感器输出电压逐渐趋于稳定,最后达到平稳状态,电压值约为2.51 V。磁通门转换系数定义为磁通门输出电压与被测磁场的比值,所以磁通门传感器灵转换系数为99.88 mV/μT。当直流电源幅度为-20 V时,流经螺线管的电流为-0.04 A,螺线管中磁感应强度为-50.27 μT,磁通门稳定输出电压为-5.1 V如图9(b)所示,所以磁通门传感器灵转换系数为101.5 mV/μT。

图9 磁通门传感器输出电压

4 磁通门传感器制备及测试

4.1 磁通门传感器制备及测试平台搭建

从钴基非晶带材上裁剪两段长度为30 mm,宽度为3 mm,厚度为25 μm的薄片,通过胶带分别粘在两块长度为32 mm,宽度为3.2 mm弧度0.8 mm的玻璃纤维薄板上。在玻璃纤维板上均匀缠绕900匝线径为0.1 mm的漆包线作为激励线圈(3层,完全覆盖磁芯)。在长度为32 mm,内径为0.5 mm外径0.7 mm的塑料管外均匀缠绕1 188匝线径为0.1 mm的漆包线作为感应线圈。将缠绕漆包线的玻璃纤维板平行固定后放入缠绕漆包线的塑料管内,如图。将初级线圈同方向两铜线线头焊接在一起,从而激励电流从一个激励线圈内流入,另一个线圈流出,即两个钴基非晶薄片沿相反方向激励。激励线圈内两磁芯实际距离约为1.2 mm。激励线圈电阻为65 Ω。

将激励线圈接入图6所示的激励电路中,并置于长1.24 m,直径20 cm的长直螺线管中间位置。激励信号是通过1 MHz晶振产生的方波信号经过7分频得到的,理论上应该是7.812 5 kHz,但实际激励信号为7.7 kHz。长直螺线管的线圈常数为41.247 m-1。为了在地磁环境中测量磁通门灵敏度,利用函数信号发生器产生一系列不同幅度、频率均为20 Hz的正弦信号接入长直螺线管,在螺线管中产生一系列不同幅度的均匀被测磁场。磁通门感应线圈输出信号通过动态信号分析仪进行频谱分析。磁通门传感器探头实物如图10所示。

图10 磁通门探头实物图

为了方便对比仿真效果,对比仿真激励电流与实际测量的磁通门传感器激励电流如图11所示。从图11可以看出仿真电流波形与实测电流波形完全一致(仿真激励信号的频率为7.812 5 kHz,实际激励信号源频率为7.7 kHz,所以在100 μs到200 μs时间段内激励电流波形完全重合,但是因为实际激励信号频率略小于仿真激励源信号频率,所以在该周期前后实测电流波形与仿真结果电流波形均略有偏移)。

图11 磁通门传感器激励电流波形

磁通门传感器的二次谐波灵敏度如图12所示,曲线斜率为17 988 V/T,对比2.2节中仿真结果,偏差均小于1.1%。误差原因是次级线圈实际匝数为1 188、实际激励信号频率为7.7 kHz,比仿真激励信号参数略小。而且仿真计算过程总也会有一定误差。

图12 磁通门传感器幅度响应曲线

磁通门传感器的频率响应曲线如图13所示,磁通门传感器的转换系数约为100 mV/μT,与3.2节中仿真结果99.98 mV/μT、101.5 mV/μT完全一致,误差均在1.5%以内,所以仿真结果是准确可靠的。

图13 磁通门传感器频率响应曲线

5 结论

磁通门磁场传感器是一种测量精度高,噪声低,稳定性好的矢量磁场传感器,它广泛应用于地磁监测、磁异常测量以及空间磁场探测等磁测领域。本文分析了平行双轴磁通门传感器的基本原理,基于Maxwell和Simplorer软件建立了磁通门传感器的探头模型和电路模型,利用两个软件的电磁联合仿真功能分析了磁通门传感器的激励电流波形、磁通门二次谐波灵敏度以及磁通门传感器的转换系数。

为验证仿真结果的正确性,利用钴基非晶薄片制作了磁通门传感器探头,利用开关电路产生的方波驱动串联电路激励磁芯材料周期性的磁化到饱和状态。利用示波器观测了激励电路波形,用动态信号分析仪观测了磁通门感应线圈输出电压频谱,测量了磁通门传感器二次谐波的灵敏度。实验测量得到的激励电流波形与仿真得到的电流波形单个周期内完全重合,灵敏度误差小于1.1%,且转换系数误差小于1.5%。仿真结果与实验测量结果完全一致。

该仿真模型简单而且准确度高,可以帮助我们更直观方便的理解磁通门传感器的工作过程,对于指导微型化磁通门传感器具有重要意义。

[1] Primdahl F. Fluxgate Magnetometer[J]. Journal of Physics E-Scientific Instruments,1979,12(4):241-253.

[2] Ripka P. Advances in Fluxgate Sensors[J]. Sens Actuator A—Phys,2003,106(1-3):8-14.

[3] Nielsen O V,Petersen J R,Primdahl F,et al. Development,Construction and Analysis of the Orsted Fluxgate Magnetometer[J]. Meas Sci Technol,1995,6(8):1099-1115.

[4] 王晓美,滕云田,王晨,等. 地磁相对记录用低噪声磁通门磁力仪[J]. 传感技术学报,2011,24(8):1158-1162.

[5] Munschy M,Boulanger D,Ulrich P,et al. Magnetic Mapping for the Detection and Characterization of UXO:Use of Multi-Sensor Fluxgate 3-Axis Magnetometers and Methods of Interpretation[J]. J Appl Geophys,2007,61(3-4):168-183.

[6] Auster H U,Glassmeier K H,Magnes W,et al. The THEMIS Fluxgate Magnetometer[J]. Space Sci Rev,2008,141(1-4):235-264.

[7] Glassmeier K H,Richter I,Diedrich A,et al. RPC-MAG—The Fluxgate Magnetometer in the ROSETTA Plasma Consortium[J]. Space Sci Rev,2007,128(1-4):649-670.

[8] Kirchhoff M R,Buttgenbach S. MEMS Fluxgate Magnetometer for Parallel Robot Application[J]. Microsyst Technol,2010,16(5):787-790.

[9] Frydrych P,Szewczyk R,Salach J,et al. Two-Axis,Miniature Fluxgate Sensors[J]. IEEE Trans Magn,2012,48(4):1485-1488.

[10] Lei C,Lei J,Yang Z,et al. A Low Power Micro Fluxgate Sensor with Improved Magnetic Core[J]. Microsyst Technol,2013,19(4):591-598.

[11] 吕辉,李随源. 低功耗微型磁通门的制备与分析[J]. 传感技术学报,2016,29(1):21-255.

[12] Felch E P,Means W J,Slonczewski T,et al. Air-Borne Magnetometers for Search and Survey[J]. Transactions of the American Institute of Electrical Engineers,1947,66(1):641-651.

[13] Gordon D I,Lundsten R H,Chiarodo R A. Factors Affecting Sensitivity of Gamma-Level Ring-Core Magnetometers[J]. IEEE Trans Magn,1965,MAG1(4):330-337.

[14] Burger J R. Theoretical Output of a Ring Core Fluxgate Sensor[J]. IEEE Trans Magn,1972,Mag8(4):791-796.

[15] Geiler A L,Harris V G,Vittoria C,et al. A Quantitative Model for the Nonlinear Response of Fluxgate Magnetometers[J]. J Appl Phys,2006,99(8):08B316-1-08B316-3.

[16] Moldovanu B O,Moldovanu C,Cretu M,et al. Nonlinear Dynamics of the Fluxgate Circuitry[J]. Sens Actuator A—Phys,1997,59(1-3):300-303.

[17] Trujillo H,Cruz J,Rivero M,et al. Analysis of the Fluxgate Response through a Simple Spice Model[J]. Sens Actuator A—Phys,1999,75(1):1-7.

[18] 侯晓伟,刘诗斌,李菊萍,等. 基于HSPICE温度对长条形磁通门输出的影响[J]. 传感技术学报,2012,25(7):941-944.

[19] 侯晓伟,刘诗斌,李菊萍,等. 磁通门的数值分析与HSPICE仿真[J]. 传感技术学报,2013,26(6):810-814.

[20] Yang S L,Liu S B,Feng W G,et al. SPICE Circuit Model of Voltage Excitation Fluxgate Sensor[J]. Iet Sci Meas Technol,2013,7(3):145-150.

叶魏涛(1989-),江西上饶人,博士研究生。研究方向为电磁场与微波技术,主要研究磁通门传感器原理及低噪声磁通门传感器研究设计等,yeweitaobarry@163.com;

朱万华(1982-),江苏扬州人,副研究员。研究方向为电磁场与微波技术,主要从事低噪声感应式线圈传感器,磁通门传感器,光泵磁力仪磁测仪器装备研制,电磁勘探方法与装备研究等,whzhu@mail.ie.ac.cn。

Transient Response Analysis of Fluxgate Magnetometer through Maxwell and Simplorer*

YE Weitao1,2,ZHU Wanhua1*,ZHANG Le1,FANG Guangyou1

(1.Key Laboratory of Electromagnetic Radiation and Sensing Technology,Chinese Academy of Sciences,Beijing 100089,China;2.University of Chinese Academy of Sciences,Beijing 100876,China)

In order to get a full knowledge of the operation principle of the fluxgate magnetometer,a magnetic circuit and electric circuit co-simulation model is established through Maxwell and Simplorer.Waveform of the excitation current andtransient response of the fluxgate magnetometer are simulated with this model. Sensitivity of the second harmonic signal and scaling factor of the fluxgate magnetic are calculated with the simulation results. A fluxgate sensor,constructed with Co-Based amorphous ribbons and driven by a switching circuit,is used to validate this model. Waveform of the measured excitation current is the same with the waveform of the simulated current,and error between the sensitivity of the simulated fluxgates and the sensitivity of the real fluxgate is less than 1.1 percent. Scaling factor is got by measuring the frequency response of the fluxgate magnetometer,and it is 100 mV/μT. It is almost the same with the simulation value,error between the two is less than 1.5 percent. This simulation model is very helpful to understand the operation principle and transient response of the fluxgate magnetometer. It would be very important when designing a micro-fluxgate magnetometer.

fluxgate magnetometer;transient response;co-simulation;sensitivity

项目来源:国家重大科研装备研制项目(ZDYZ2012-1-05-02);国家自然科学基金项目(41374186)

2016-12-22 修改日期:2017-03-10

TP212.1;TM936.2

A

1004-1699(2017)07-1022-07

C:7230;7310L

10.3969/j.issn.1004-1699.2017.07.009