基于小波包与SOM神经网络的传感器故障诊断*

李娟娟,孟国营,谢广明,贾一凡

(1.中国矿业大学(北京)机电信息与工程学院,北京 100083;2.北京大学工学院,北京 100871)



基于小波包与SOM神经网络的传感器故障诊断*

李娟娟1*,孟国营1,谢广明2,贾一凡1

(1.中国矿业大学(北京)机电信息与工程学院,北京 100083;2.北京大学工学院,北京 100871)

研究传感器实时故障诊断问题。首先采用MATLAB2015仿真得到传感器各种典型工作状态下的运行数据样本;其次将这些故障样本作3层小波包分解,分别求出第3层小波包基对应的各频率段的能量,利用这些能量值与正常工作时各频段的能量值之比构造出传感器故障诊断的特征向量;最后构建基于3×3的SOM神经网络的传感器故障诊断算法。测试证明了所提算法的有效性和准确性。

传感器;小波包变换;SOM神经网络;故障样本;故障诊断

在自动控制领域,传感器是不可或缺的硬件之一,它是获取信息的主要装置。若传感器性能蜕化、产生故障或者失效,提供的信息偏离真实数据,将会对系统的其他环节如自动控制、故障诊断等带来严重影响[1]。自动化系统的安全性、可靠性和整个生产的效能很大程度上取决于传感器的精度和可靠性。然而,传感器比系统中的其他部分更容易出现故障[2]。据美国“智能维护系统中心”研究表明:一般自动化系统40%以上的故障皆是由于传感器系统自身的故障而产生[1]。及时准确识别系统的故障源然后实施相应的对策可以避免昂贵的系统停机成本,甚至更为严重的安全事故。因此,研究如何及时发现、快速诊断传感器故障具有十分重要的意义。

本文利用三层小波包分解,提取第3层各频率段的能量、归一化处理后作为故障模式的特征值输入SOM(自组织竞争)神经网络进行传感器故障诊断。这种直接利用各节点能量的方法更能直接反映故障信号的瞬态特征,而且应用方便。

1 小波包与特征提取

传统的傅里叶分析只在频域范围进行,丢失信号的时域信息,而小波变换是一种信号的时频分析方法。另外,短时傅里叶变换只能在单一的分辨率下进行分析,而小波分析能进行多分辨率分析,而且在时域和频域都具有表征信号局部信息的能力。小波包分析能为信号提供一种更精细的分析方法,它将频带进行多层次划分,对多分辨率分析中没有细分的高频部分进一步分解,并能够根据被分析信号的特征,自适应地选择相应的频段,使之与信号频谱相匹配,从而提高了时频分辨率[3-4]。

1.1 小波包理论

小波分析的思想是用小波函数系表示或逼近一个信号或函数。小波函数系是由满足一定条件的基本小波函数经过平移和伸缩构成。小波函数系表示的特点是它的时宽和频宽的乘积很小,且在时间和频率轴上都很集中。但是,正交小波基的一个缺点是其高频处时间分辨率高,频率分辨率却降低[4]。小波包通过增加分辨层数,对变宽的频谱窗口进一步分割变细,克服这一缺陷。对某个给定的信号,通过一组低、高通组合正交滤波器H、G,能够将信号划分到任意频段上。以三层小波包分解为例,信号x(t)的划分过程如图1所示。图1中,H表示低频,G表示高频[5-6]。

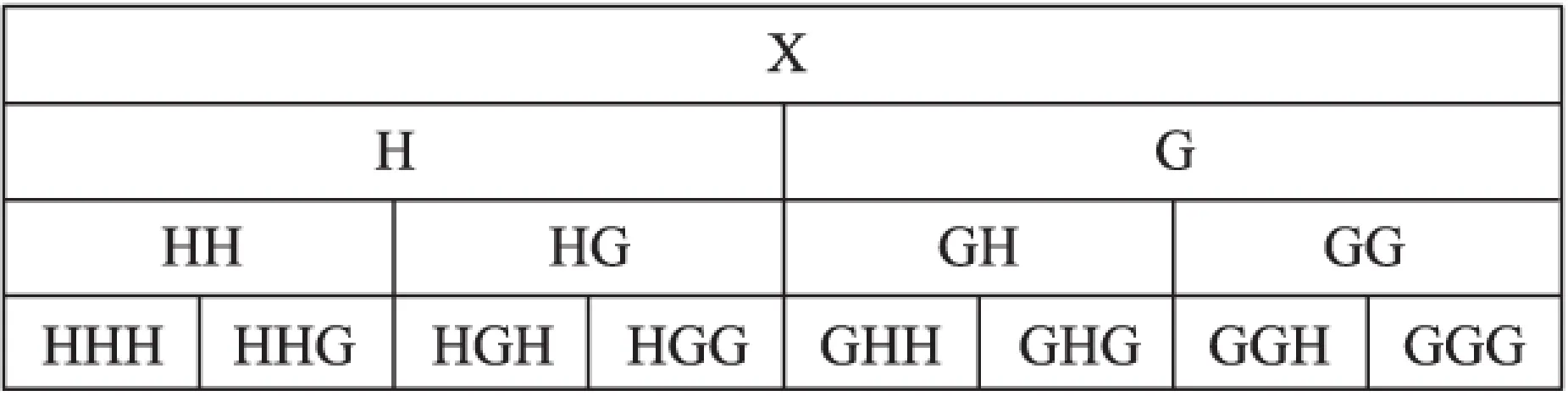
图1 小波包分解过程

1.2 特征提取

传感器故障分为突发型故障(abrupt)和缓变型故障(incipient)。本文以传感器的突发型故障中的漂移、偏置、周期性干扰为例进行研究。传感器发生突变型故障后,输出的数据会发生一些瞬变,即使发生的变化很小,其中也包含了传感器故障的重要信息[7-10]。对传感器各频率成分能量进行特征提取,由于各频率成分能量蕴含的故障信息,不同频率成分能量的改变代表不同的故障,通过分析各频率段的能量,可以对传感器的故障做出诊断。

传感器信号x(t)∈L2(R)的小波包系数由式(1)计算:

(1)

(2)

不同的传感器故障有不同的信号变化模式,为检测和量化这些模式,针对不同小波包结点上信号能量的不同,本文利用小波包变换对原始信号进行了3层分解(j=3、n=0,1,…,7、k=1,…,m),分别计算第3层各频率段的能量,利用这些能量值与正常工作时各频段的能量值之比则可以构造出传感器故障模式判别的特征向量:

(3)

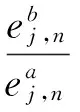
2 SOM神经网络

2.1SOM神经网络结构

自组织映射神经网络,即SOM(SelfOrganizingMaps),可以对数据进行无监督学习聚类。该网络是一个由全连接的神经元阵列组成的自组织、无教师学习网络。SOM神经网络在对外部输入信息形成拓扑映射结构的过程中,具有和人脑信息映射相类似的两个特点[11-12]:①拓扑映射结构不是通过神经元的移动重新组织实现的,而是由各个神经元在不同兴奋状态下构成一个整体所形成的拓扑结构。②这种拓扑映射结构的形成具有自织特点。因此,SOM神经网络算法和有监督学习的方法相比更接近人脑的认知过程。SOM神经网络由输入层和竞争层组成。其结构如图2所示。

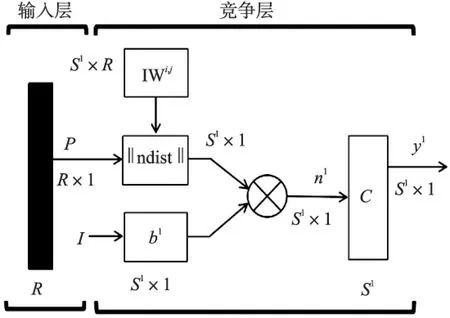
图2 SOM神经网络的结构

SOM神经网络的学习映射由最佳匹配神经元的选择和权向量的更新两部分构成。图2中,输入p为R维向量,表示待分类的特征空间是R维的(每个样本有R个分量),权值IW也是R维向量,与输入向量的维数相同;‖ndist‖计算输入向量p和输入权值向量IW之间的距离,其输出为s1×1的列向量,列向量的每个元素为输入向量p和输入权值向量IW距离的负数。n1为竞争层神经元函数的输入,其值为输入向量p和输入权值向量IW距离的负数与阈值b1的和。对于n1中最大的元素即竞争的“获胜者”,该神经元及其邻域内的神经元权向量朝着与模式向量更接近的方向更新,其他神经元的权值向量保持不变。不断重复这种竞争和权向量的更新,最终神经元就会学会模式向量,并以权向量的形式保存下来,从而实现对模式向量的聚类、识别与拓扑不变性映射等。这一过程就是自组织学习映射[13]。

2.2 SOM神经网络的学习算法

SOM神经网络的学习算法如图3所示。

图3 SOM神经网络的算法流程图

具体描述如下:

①开始,确定聚类类别数,即类别向量的维数C,模‖·‖,及误差阈值ε,ε是大于0的小常数。

②初始化权向量W(W1,W2,…,Wc),学习率αj(0),邻域大小Nj(0),设定最大迭代次数tmax,令迭代计数器t=0。

③计算输入模式向量Xk与全部输出神经元权向量Wj的距离d。

④选择具有最小距离的神经元,若j获胜:dj=min{d}。

⑤更新获胜神经元j及其邻域内神经元权向量:

Wj(t)=Wj(t-1)+αj(t-1)[Xk-Wj(t-1)];更新j的学习率αj(t)及邻域大小Nj(t);计算:

⑥若E(t)≤ε则停止,否则t=t+1转至(3)进行下一次迭代。

3 仿真实验与分析

3.1 仿真实验

仿真实验用MATLAB2015模拟传感器3种故障以及正常工作状态下的输出,并在传感器的输出信号中加入高斯白噪声来模拟系统噪声。仿真共得到4种状态下的128组故障样本[14-16]。根据这些故障样本的频带特点,把样本信号作 3 层小波包分解,得到 8 个频率范围无重叠的小波包基,再分别求出这 8 个小波包基对应的各频率段的能量,利用这些能量值与正常工作时各频段的能量值之比构造出传感器故障诊断的特征向量。取每个故障状态下的前30组故障特征向量作为训练样本,后两组作为测试样本。

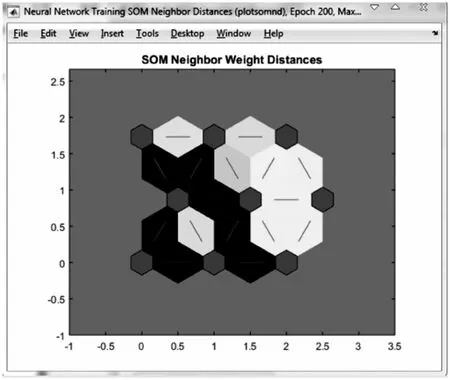
图5 相邻神经元间的权值距离

针对以上样本,SOM网络的竞争层采用3×3排列的神经元,其拓扑结构采用六边形结构(hextop),输入向量的训练次数设置为200,邻域大小初始值为3,神经元距离采用linkdist。为防止输入样本数据间的偏差过大,在创建网络时先对其进行归一化处理。图4为SOM神经网络的训练过程记录。该网络训练后得到的相邻神经元的权值距离如图5所示,各神经元上的样本点数如图6所示。

图4 SOM的训练过程记录

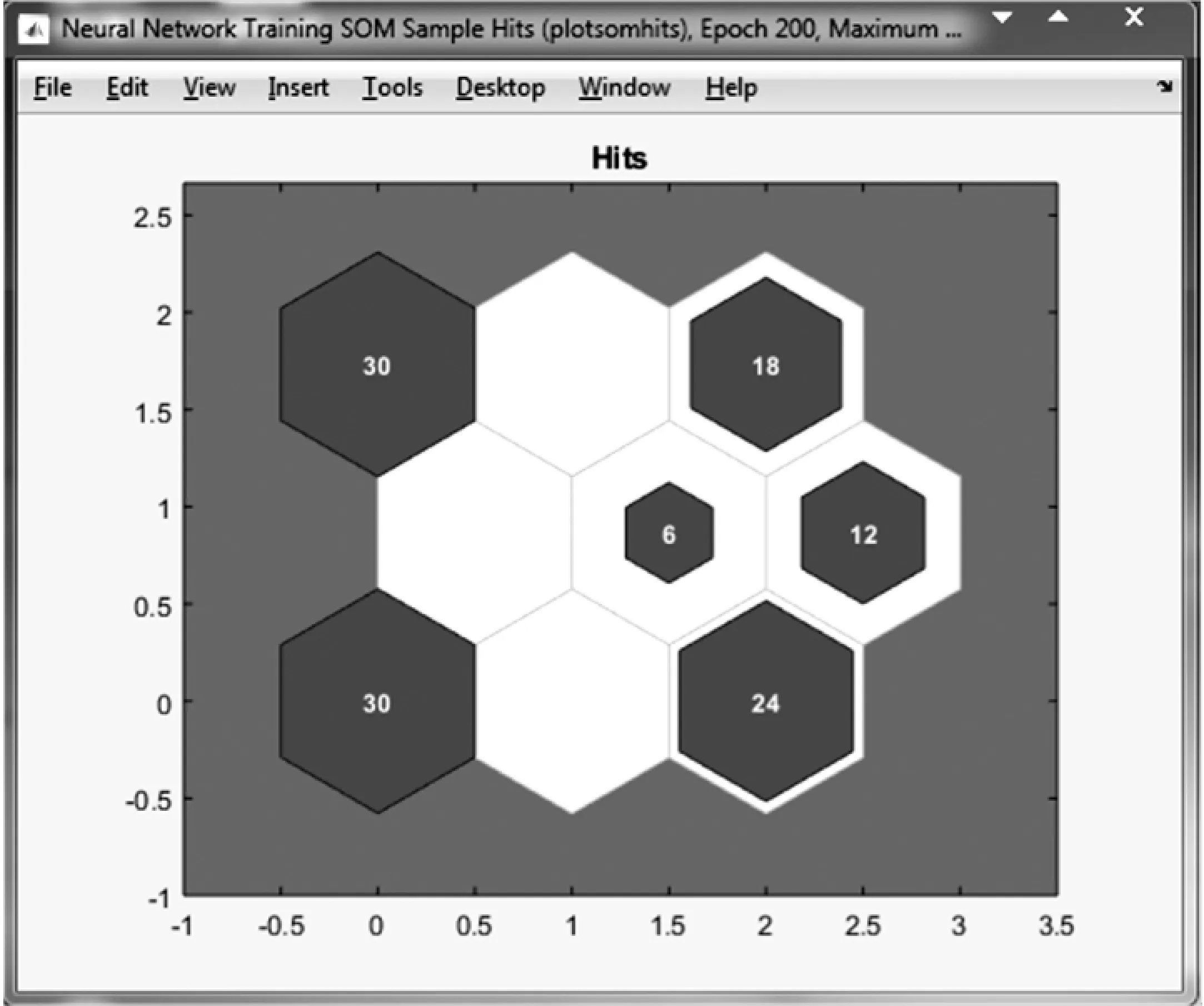
图6 网络样本点数

程序输出其分类后结果如表1所示,其中,7代表周期性故障,1代表漂移故障,9和6代表偏置故障,3和5代表无故障。

表1 分类结果

为验证该网络对故障诊断效果,分别采用表2所示的8组数据进行测试。将这些数据输入到训练好的SOM神经网络中,网络检验结果如图7所示。

从图7可以看出,第1、2组样本对应的网络输出为7,第3、第4组样本对应的网络输出为1,第5、第6组样本对应的网络输出为9,第7、第8组样本对应的网络输出为3。也就是说通过网络的分类判别,第1、第2组样本为周期性故障,第3、第4组样本为漂移故障,第5、第6组样本为偏置故障,第7、第8组样本为无故障。所有测试样本均得到正确的分类,说明设计算法的有效性。

图7 检验结果输出

3.2 实验分析

①小波包分解时,小波函数的选取对故障诊断结果的影响很大。同样的故障样本信号选取不同的小波函数时,诊断的准确率可能会在80%～100%之间变化。

②由于原始信号中随机噪声的加入、仿真时偏置故障的偏置设置较小等原因,导致在用SOM神经网络进行模式分类时,可能产生传感器的正常运行数据和偏置故障之间存在误诊,但总体来说诊断准确率在95%以上,可以达到辨识分类的要求。

表2 能量变化率特征向量

4 结论

本文针对传感器常见的周期型、漂移型和偏置型故障,首先,采用MATLAB2015仿真得到传感器各种运行状态下的运行数据,将这些数据中加入高斯白噪声后作为判断传感器运行状态的故障样本。然后,将这些故障样本信号作3层小波包分解,得到8个频率范围无重叠的小波包基,再分别求出这8个小波包基对应的各频率段的能量,利用这些能量值与正常工作时各频段的能量值之比构造出传感器故障诊断的特征向量。最后构建3×3的SOM神经网络进行模式分类与故障诊断,并通过测试证明了算法的有效性和准确性。

[1] 张娅玲,陈伟民,章鹏,等. 传感器故障诊断技术概述[J]. 传感器与微系统,2009,15(1):4-12.

[2] 付克昌. 基于结构优化PCA的传感器故障诊断方法及其应用研究[D]. 杭州:浙江大学,2007.

[3] 徐涛,王祁. 基于小波包神经网络的传感器故障诊断方法[J]. 传感技术学报,2006,19(4):1060-1064.

[4] 夏利民. 基于Kohonen神经网络的滚动轴承故障诊断[J]. 计算机工程,2003,29(3):39-41.

[5] 李文军,张洪坤,程秀生. 基于小波和神经网络的传感器故障诊断[J]. 吉林大学学报(工业版),2002,34(3):491-495.

[6] 王军号,孟祥瑞,吴宏伟. 基于小波包与EKF-RBF神经网络辨识的瓦斯传感器故障诊断[J]. 煤炭学报,2011,36(5):866-872.

[7] Samir Abdelmalek,Linda Barazane,Abdelkader Larabi,et al. A Novel Scheme for Current Sensor Faults Diagnosis in the Stator of a DFIG Described by a T-S Fuzzy Model[J]. Measurement. 2016,91:680-691.

[8] Hang Geng,Yan Liang,Feng Yang,et al. Model-Reduced Fault Detection for Multi-Rate Sensor Fusion with Unknown Inputs[J]. Information Fusion 2017,33:1-14.

[9] 赵成伟,叶志锋,王继强,等. 涡扇发动机传感器故障诊断的快速原型实时仿真[J]. 航空动力学报,2014,29(2):451-457.

[10] 李睿,郭迎清,吴文斐. 航空发动机传感器故障诊断设计与验证综合仿真平台[J]. 计算机测量与控制,2010,18(3):527-529.

[11] 温新,李新,张兴旺,等. 应用MATLAB实现神经网络[M]. 北京:国防工业出版社,2015:239-288.

[12] 张德丰.MATLAB神经网络仿真与应用[M]. 北京:电子工业出版社,2009:193-216.

[13] 张德丰,许华兴,王旭宝,等. MATLAB小波分析[M]. 第2版,北京:机械工业出版社,2012:32-314.

[14] 陈伟宏,李仁发. 无线传感器网络仿真技术综述[J]. 控制工程,2014,21(2):149-155.

[15] 何保成,于达仁,史新兴. 应用传感器仿真模型分析发动机控制系统故障[J]. 推进技术,2001,22(5):364-367.

[16] 龚亚信,杨宏文,郁文贤. 检测前跟踪应用中的传感器观测数据仿真研究[J]. 系统仿真学报.2009,21(22):7293-7306.

李娟娟(1976-),女,高级工程师,博士研究生,机械电子专业,研究方向为设备故障诊断,673958678@qq.com;

孟国营(1963-),男,博士,教授,博士生导师,现任中国矿业大学(北京)科学技术研究院院长,研究方向为系统动力学、测试计量技术及智能化仪器、设备故障诊断与状态检测,mgy@cumtb.edu.cn;

谢广明(1973-),男,北京大学工学院教授,博士生导师,研究方向为混杂切换系统理论,网络化控制系统,多机器人协调控制,智能控制系统,xiegming@pku.edu.cn。

Sensor Fault Diagnosis Based on Wavelet Packetand SOM Neural Network*

LI Juanjuan1*,MENG Guoying1,XIE Guangming2,JIA Yifan1

(1.School of Mechanical Electronic and Information Engineering,China University of Mining and Technology(Beijing),Beijing 100083,China;2.College of Engineering,Peking University,Beijing 100871,China)

Sensor fault diagnosis is investigated. First,sensor’s fault samples under various operation conditions are obtained by simulation with the MATLAB2015. Then fault samples are decomposed by a three-layerwavelet packet decomposition technology,and the energies of corresponding frequency in third layer are obtained,respectively. Eigenvector of sensor fault diagnosis is extracted by using the ratio between fault energies and faultlessenergies on various frequencies. Finally,a 3 by 3 SOM neural network based algorithm isproposed for pattern classification and fault diagnosis. The effectiveness and accuracy of the proposed method are illustrated by diagnostic results.

sensor;wavelet packet transformation;SOM neural network;fault samples;fault diagnosis

项目来源:国家“十三五”重点研发计划项目(2016YFC0600900);国家自然科学基金项目(U1361127)

2016-12-22 修改日期:2017-02-20

TP183

A

1004-1699(2017)07-1035-05

C:7230

10.3969/j.issn.1004-1699.2017.07.011