注重基本图形教学 提升学生解题能力——以“‘一线三等角’基本图形及其应用”教学为例

李广伟

注重基本图形教学 提升学生解题能力
——以“‘一线三等角’基本图形及其应用”教学为例

李广伟

在几何教学中，将同种类型的问题进行合理归纳、梳理，进而形成一个基本的图形，对提高课堂效率和学生的数学解题能力有很重要的作用。以“‘一线三等角’基本图形及其应用”教学为例，对基本几何图形的抽取过程进行提炼和总结，对学生认识基本图形、运用基本图形、探究基本图形给予帮助。

基本图形；一线三等角；教学效率；解题能力

《义务教育数学课程标准（2011年版）》指出：几何直观主要是指利用图形描述和分析问题。借助几何直观可以把复杂的数学问题变得简明、形象，有助于探索问题解决的思路，预测结果。几何直观可以帮助学生直观地理解数学，在整个数学学习过程中都发挥着重要作用。要想提高学生的几何直观能力，教师需要有意识地加强基本图形的教学。有论者认为，平面几何中的基本图形分为两类，现行教材中概念、公理、定理所对应的图形称为理论性基本图形，课本中具有一定典型性的例题、习题所对应的图形称为经验型基本图形。“一线三等角”就属于第二种基本图形。

一、活动探究，归纳基本图形

活动一：将三角板的直角（∠C）顶点放在直线l上 （直角边不与直线l重合），在两条直角边所在的射线上任取两点A、B，分别过点A、B作 AM⊥l于 M，BN⊥l于N。观察你画出的图形，你有什么发现？若CM=CN，连接AB，你有什么新发现？

设计意图：从学生熟悉的图形开始，努力让所有学生积极参与到课堂中来，鼓励学生打破固定的思维方式，尽可能想到不同的构图方式；虽然构图不同，但是证明思路一致，通过观察，描述这类相似模型的共同特征。在两种不同图形的基础上构造CM=CN，学生会很快发现，当直线l在直角内部时，此时的图形会是射影定理的基本图形，而新的发现就是三个直角三角形都相似。

活动二：将60°角（∠XCY）的顶点放在等边三角形PMN的一边MN上 （角的两边不与直线MN重合），直线XC、YC分别与直线PM、PN交于A、B两点。观察你画出的图形，你有什么发现？若CM=CN，连接AB，你有什么新发现？

活动三：将45°角（∠XCY）的顶点放在等腰三角形PMN的底边MN上（角的两边不与直线MN重合），∠XCY=∠M，直线XC、YC分别与直线PM、PN交于A、B两点。观察你画出的图形，你有什么发现？若CM=CN，连接AB，你有什么新发现？

设计意图：在活动一的基础上做出变化，让学生组内互助合作，构造出不同的图形，说明其解决问题的方法。引导学生找出3种情况下构造出的图形的共同点，体会直角、60°角、45°角所起的作用。鼓励学生自己独立解决问题，大胆假设，类比验证，在活动中体验从特殊到一般的数学思想。教师在学生充分讨论的基础上，小结出一类相似模型的共同特征：顶点在一条直线上的三等角可推出△ABP∽△PDC；三等角加上一组对应边相等可推出△ABP≌△PDC。如图1所示。

二、由浅入深，提升学生运用基本图形解题的能力

通过以上的对比归纳，学生对“一线三等角”这个基本图形有了初步的认识。下面通过有梯度的题组练习让学生感受基本图形在解题中的作用，实现学生对基本图形的内化，逐步达到能够将基本图形作为一个思维单元运用到解题过程中去。

1.如图2，在矩形ABCD中，点F为边CD上一点，沿AF折叠，点D恰好落在BC边上的E点处，若 AB=3，BC=5，CF=_______。

2.如图 3，在△ABC 中，∠BAC=60°，∠ABC=90°，直线 l1∥l2∥l3，l1与 l2之间距离是 l，l2与 l3之间距离是 2，且 l1，l2，l3分别经过点 A，B，C， 则边AC的长为________。

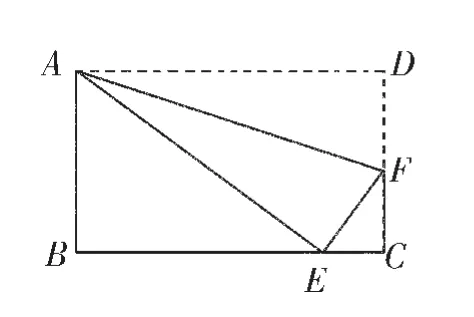
图2

图3

设计意图：练习1含有显性基本图形，这样既便于学生从复杂背景中迅速抓住基本图形，又能够有助于学生理解复杂的题目是由基本图形、基本问题构成的；同时还能够使学生体会到将基本图形作为一个思维单元给解题带来的便捷，获得成功体验。通过解决这个问题，学生获得了初步的解题经验，即抓住基本图形，能够促进有效解题。练习2不含显性基本图形，但问题中隐藏着基本图形，在解题时要引导学生发现这些基本图形的“影子”，并把这些基本图形挖掘出来，适当补充完整，再应用相应的结论来解决问题。通过这组练习，学生对利用基本图形解题有了更加深刻的认识。将复杂问题的图形转化为基本图形就变成了我们所熟悉的简单问题，由此激发学生更深层次的探究，即挖掘数学知识、图形间的内在联系，透过变化的现象看到不变的本质，更加提高了学生的解题能力。

三、化繁为简，构造基本图形解决问题

教学进行到第三个环节，需要进一步引导学生体会利用掌握的基本图形进行解题的优越性。可以呈现如下例题：

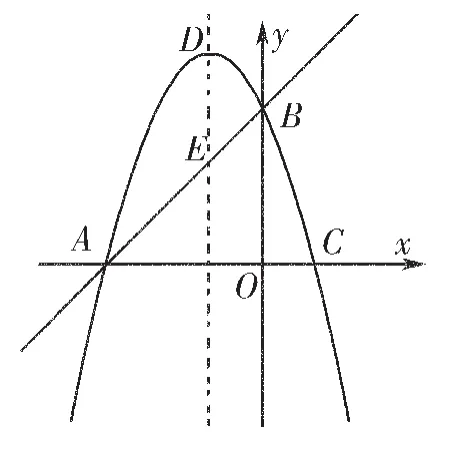
图4

如图4，已知直线y=x+3与x轴交于点A，与y轴交于点 B，抛物线y=-x2+bx+c经过 A、B两点，与x轴交于另一个点C，对称轴与直线AB交于点E，抛物线顶点为D。 （1）写出 A、B、C、D 的坐标；（2）点 P 从点 D 出发，沿对称轴向下以每秒1个单位长度的速度匀速运动，设运动的时间为t秒，当t为何值时，以P、B、C为顶点的三角形是直角三角形？直接写出所有符合条件的t值。

对于本题的第2问，一般的解题思路是利用勾股定理， 分∠PBC=90°、∠BCP=90°和∠BPC=90°三种情况讨论，运算较为烦琐。而通过构造“一线三等角”的基本图形，则可以利用相似三角形的性质，很容易得出答案。在教学中让学生对运用基本图形的解题方法与运用勾股定理列方程的方法进行比较，让学生体会运用基本图形解决问题所带来的优越性。

综上，在几何教学中，教师应当有意识地培养学生对几何图形的识别、构造、组合与分解的能力。教师应当注意基本图形教学的直观性、形象性，从最简单、基础的基本图形入手，让学生在脑海中形成各种基础的直观图形，在实际运用中利用或构造基本图形解决问题，这是提高学生解决与图形有关问题的能力的重要途径。

［1］张俊.基于案例分析的初中数学几何基本图形教学探索［J］.兵团教育学院学报，2015（02）.

［2］殷宪刚.浅议中学数学基本图形教学［J］.课程教育研究，2015（04）.

G633.6

A

1005-6009（2017）43-0036-02

李广伟，江苏省苏州市高新区第二中学（江苏苏州，215219）教师，高级教师，苏州市学科带头人。