从“一维”到“二维”的长方形面积教学
浙江省义乌市赤岸小学 朱惠霞
从“一维”到“二维”的长方形面积教学
浙江省义乌市赤岸小学 朱惠霞
关于“长方形、正方形的面积计算”教学会有这样的争论:有的人认为长方形的面积计算公式可以通过推导得出:长几表示长边可以放几个面积单位,宽几可以表示宽边可以放几个面积单位,最后通过乘法计算出面积。通过教学要让学生明白为什么长乘宽等于长方形的面积。也有另一拨人认为长方形的面积公式怎么可能在小学被推导出来?长度不够整数怎么办?假设长度是怎么办?它的推导需要应用极限的知识。长方形的面积计算在小学里只能视作一种公理,无法推导。因此,长方形的面积计算的设计思路应该是实验——猜想——验证——概括,像这样的不完全归纳。我在教学操作中,同样把长方形的面积计算公式作为公理对待,同样启发学生明白为什么长乘宽(整数数据)等于长方形的面积。在侧重培养“空间观念”、“空间能力”的思考下演绎出了不一样的课。
一、在操作中积累空间知觉,强化面积单位的表象
上课开始,我引导学生进行了两个重要的操作。
操作1:我们学具袋里有小方块,打开看看,你觉得这里有1平方厘米吗?怎样才能验证它是1平方厘米?
操作2:用这些小方块去求出1号长方形的面积是多少。方法越简单越方便越好。

【这两个操作可谓是整节课的基础。它让学生再次感知了长度单位和面积单位的关系,面积和面积单位的关系,同时也强化了之前建立起来的面积单位的表象。】
二、在反馈中形成表象,为发展想象做准备
1.交流铺满。
师:面积是多少?
生:15平方厘米。
师:也就是说这个长方形里可以摆满15个1平方厘米。这15个怎样数比较方便?
生:三五十五。

师:三五十五说明这里有3个5。你看到了没有?我们一起来数数看:1个5,2个5,3个5。【在这个反馈交流中,学生形成几个几排列的表象。】2.交流半铺。
师:刚才我发现有些同学是没有铺满的,也能求出15平方厘米,是怎么回事?
生:横着摆3个,竖着摆5个就能知道有多少了。
师:谁听明白他的意思了?(停顿)能用一个算式表示它的想法吗?生:3×5=15(平方厘米)。
师:乘法一般表示几个几,它表示几个几?第一个5在哪里?第二个5呢?还有一个呢?
师小结:没有铺满,我们可以推断出它铺满是多少,厉害!这样我们就可以不用摆那么多1平方厘米了。
3.交流用一个小方块去量。
师:他只用了8个,还有没有用得更少的?
生:1个。
生:1个都没有!
师:用1个?你是怎么想的?
生:就用1个小方块先横着摆过去,再竖着摆过去,就知道面积是多少了。

师:谁懂他的意思了?这样摆怕一下子忘了横着摆几个了,谁有好办法?
生:摆一个做一个记号。
4.交流不铺。
师:一个都没有是怎么回事?

生:用尺子量。
师:用尺子量能量出面积吗?你们也用尺子量量看,认为能量出来的举手?
师:谁来说说你是怎么想的?
【操作反馈的教学从“全铺——半铺——用一个面积单位量——不铺”四个层次展开。虽然小方块是一块一块地拿走,但其“3个5”全铺的动态过程被不断地重现。最后虽然不铺了,用尺子量,孩子也会自动呈现全铺的动态过程。这为接下来“几个几”的想象奠定了表象基础,同样为帮助长方形的面积计算实质是面积度量奠定了意义基础。】

三、在想象中促成两次飞跃
1.有了3个5这个表象基础,紧接着我出示了长5厘米,宽2厘米的长方形,让学生量出它的面积。思考:为什么宽少了1厘米,面积会少了5个?这样的练习促成了孩子初步的想象,促进直接度量到间接度量的过渡。
2.出示一个长方形,用尺子量出这个长方形的长是10厘米。你想到了什么?(根据学生回答依次出示后两张幻灯片)


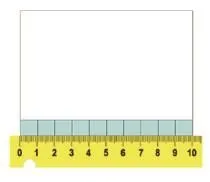
3.出示宽8厘米,你想到了什么?(根据学生回答,依次出示后两张幻灯片)


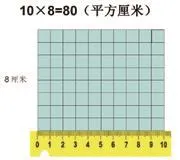
【今后我们碰到解决长方形的面积问题都是提供数据的“间接计算”得出结果,很少会再碰到用面积单位的直接度量。但尺子几乎每天都陪伴着学生们,是最便捷的直观工具,它是完成直接度量到间接计算飞跃很好的认知材料。尺子像小方块一样从有到无,目的就是为了把尺子这种印象刻画在脑海里,形成长度单位的表象,建立长度单位和面积单位的关系,从而很好地衔接了这次飞跃。】
四、在想象推理中建立二维空间观念,突破一个难点
1.二维空间的建立。
师:这里有一个长方形,它的长是9厘米,你能想到什么?(只出示数据不出示图形)
生:横着可以摆9个。
师:能想到它的面积吗?为什么?
生:不能。宽不知道。
师:宽不知道,就不知道要摆几行了?那么告诉你宽是4厘米,你能想到什么?
【我们要注重二维、三维空间观念的建立。在六年级“常见的量”总复习的教学实践中我们会发现,这种观念欠缺的孩子会出现下面这样的错例。】
认为面积单位的进率如图(1),体积单位间的进率如图(2)。
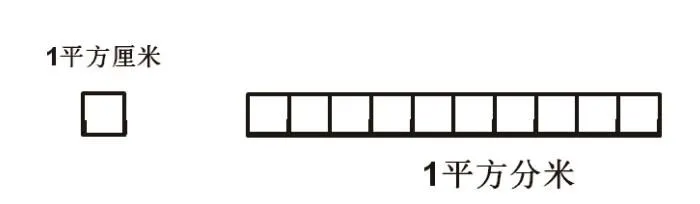
图(1)

图(2)
2.借助“间接度量”到“间接计算”的思维提升,突破“统一长度单位计算”的难点。
师出示:长9分米,宽4分米的长方形(只有数据没有图)。师:这个跟刚才的长方形有什么不同?你能想到什么?长9米,宽4米呢?
师:比较这三个长方形有哪些共同点。不同点在哪里?它们的单位和什么有关?有什么关系?
师:能用2×3=6来算吗?为什么?


师:你觉得这个长方形用哪个面积单位去量比较合适?
根据学生的回答出示这样的幻灯片。
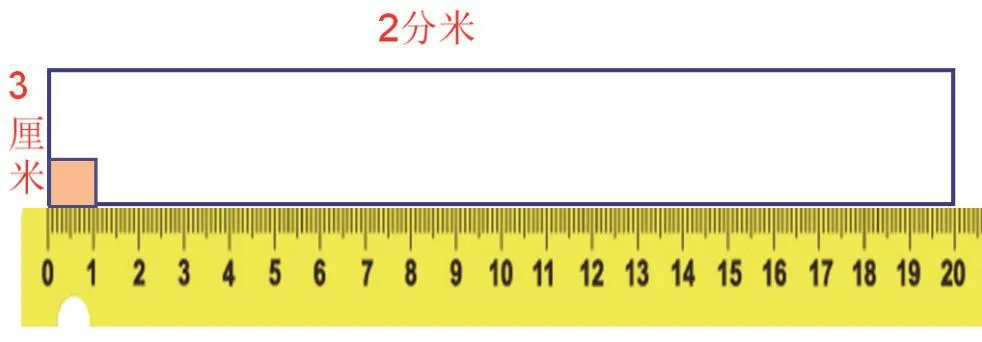
【以前我们只知道要求学生统一单位计算,而为什么要统一单位,学生对此还是很困惑的。“长2分米,宽3厘米的长方形面积为什么不是3×2?”这道题说明了“间接计算”比起用尺子“间接度量”它更加抽象,有尺子的长方形相对来说是直观的。“间接度量”到“间接计算”是需要以尺子的表象为支点(或者说单位的表象)跨过来的。这个跨越分成了三个层次:(1)有尺子的10厘米到没尺子的8厘米的出现。(2)由长和宽是什么长度单位去想象相应的面积单位。(3)思考单位不一样,选择怎样的面积单位比较合适。相信借助“尺子”表象的建立,通过想象推理,学生会发现边长用什么长度单位随之会对应一个什么样的面积单位。当长和宽的单位不一样时,需要统一单位才能想象推理出它的面积是多少。】
3.练习二维和一维的转化,强化一维和二维的联系。
到课最后出示了这样一个开放式练习:
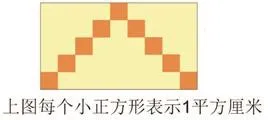
根据这幅图你想到了什么?想得越多,说明你这节课学得越好。孩子会想到面积,想到边长,又进而想到周长。
从一维的长度想到二维的面积是这节课的难点,整堂课通过操作、建立表象、想象推理,借助尺子等材料突破了“直接度量”到“间接计算”的飞跃,同时培养了孩子的空间能力,最后从二维想到一维又是认识的升华。当思维能自如地在一维和二维之间互相转化时,长方形面积公式的归纳也是水到渠成的事。在度量几何的教学中,这样的一节课的意义是非凡的。

