求函数解析式的常用方法

甘肃省陇南市武都八一中学 尹 鑫

求函数解析式的常用方法

甘肃省陇南市武都八一中学 尹 鑫

当前，我们已进入高三一轮复习，函数是高中数学的核心内容，也是学习高等数学的基础，是数学中最重要的概念之一，它贯穿中学数学的始终。求函数解析式是函数部分的基础，在高考试题中多以选择、填空形式出现，属中低档题目，同学们务必要拿分。下面就向同学们介绍几种求函数解析式的常用方法：

【题型一】配凑法

例1 已知f（x+1）=x+2，求f（x）。

分析：函数的解析式y=f（x）是自变量x确定y值的关系式，其实质是对应法则f：x→y，因此解决这类问题的关键是弄清对“x”而言，“y”是怎样的规律。

解：∵f（x+1）=x+2=（x+1）+1

令t=x+1，则f（t）=t+1，

∴f（x）=x+1。

小结：此种解法为配凑法，通过观察、分析，将右端“x+2”变为接受对象“x+1”的表达式，即变为含（x+1）的表达式，这种解法对变形能力、观察能力有一定的要求。

【题型二】换元法

例2 已知f（1-cosx）=sin2x，求f（x）。

分析：视1-cosx为一个整体，应用数学的整体化思想，换元即得。

解：令t=1-x，0≤t≤2，

则cosx=1-t，

f（t）=sin2x

=1-cos2x

=1-（1-t）2

=1-1+2t-t2

=-t2+2t。

故f（x）=-x2+2x，（0≤x≤2）。

小结：①已知f[g（x）]是关于x的函数，即f[g（x）]=F（x），求f（x）的解析式，通常令g（x）=t，由此能解出x=（t），将x=（t）代入f[g（x）]=F（x）中，求得f（t）的解析式，再用x替换t，便得f（x）的解析式。注意：换元后要确定新元t的取值范围。

②换元法就是通过引入一个或几个新的变量来替换原来的某些变量的解题方法，它的基本功能是：化难为易、化繁为简，以快速实现未知向已知的转换，从而达到顺利解题的目的。常见的换元法是多种多样的，如局部换元、整体换元、三角换元、分母换元等，它的应用极为广泛。

【题型三】待定系数法

例3 设二次函数f（x）满足f（x+2）=f（2-x），且f（x）＝0的两实根平方和为10，图象过点（0，3），求f（x）的解析式。

分析：由于f（x）是二次函数，其解析式的基本结构已定，可用待定系数法处理。

解：设f（x）＝ax2+bx+c（a≠0），

由f（x+2）=f（2-x）可知，该函数图象关于直线x=2对称，

∴-b/2a=2，即b=-4a……①，

又图象过点（0，3），∴c=3……②，

由①②③解得a=1，b=-4，c=3，

∴f（x）=x2-4x+3。

【题型四】消元法

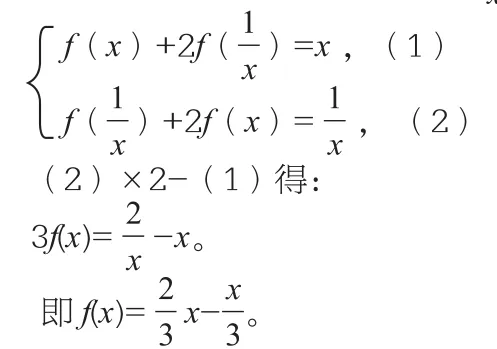
【题型五】赋值法

此类解法的依据是：如果一个函数关系式中的变量对某个范围内的一切值都成立，则对该范围内的某些特殊值必成立，结合题设条件的结构特点，由特殊到一般寻找普遍规律。

例5 已知f（0）=1，f（x+y）-2f（x-y）=x（x-y）+2xy-1（x，y∈R），求f（x）。

解：令y=0，则f（x）-2f（x）=x-1，

所以f（x）=1-x。

评析：将适当变量取特殊值，使问题具体化，简单化，依据结构特点，从而找出一般规律求出解析式。