圆方之间—椭圆与长方形

天津职业技术师范大学(300222) 闫晓玲

圆方之间—椭圆与长方形

天津职业技术师范大学(300222) 闫晓玲

给出了椭圆的一种描点作图方法,并证明了椭圆上任一点与轴的两端点的连线及连线的延长线截轴和外切长方形边所得的对应线段比等于对应的两轴比.特殊情况下截点是各自线段上相同等分的对应分点.

椭圆 长方形n等分 对应分点 定比分点

我们知道椭圆是有边界的,分别以椭圆的长轴、短轴为长、宽的长方形就是它的范围.即对椭圆而言,它上任一点(x,y)的坐标满足|x|≤a,|y|≤b.并且我们利用这个长方形可以大致画出椭圆的草图.事实上这个椭圆草图可以画得更规范点.

一、由已知长方形描绘其内接椭圆的草图

已知长方形ABCD,长、宽分别为 2a、2b,E、F、G、H分别是边AB、BC、CD、DA上的中点,连接EG、HF,两线交于点O,如图1所示.将OF四等分,分点记为R、S、T;将CF四等分,分点记为R′、S′、T′.连接ER并延长、连接GR′,两线交于点L;连接ES、GS′,得交点M;连结ET、GT′,得交点N.用弧线顺次连结G、L、M、N、F,得到的椭圆,如图1.

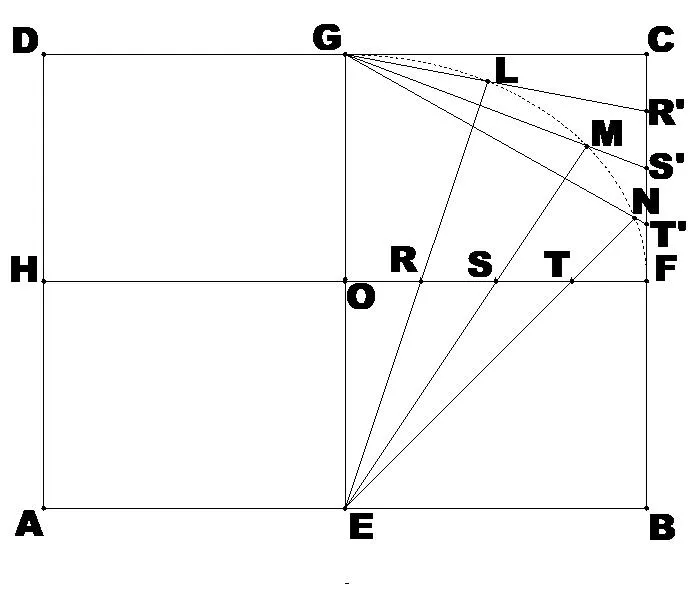
图1

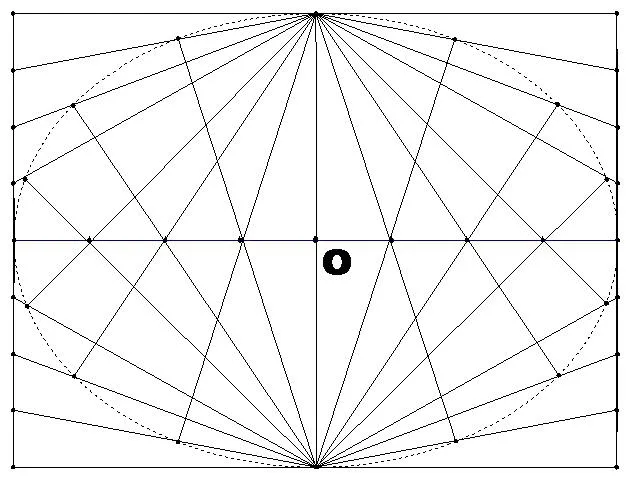
图2

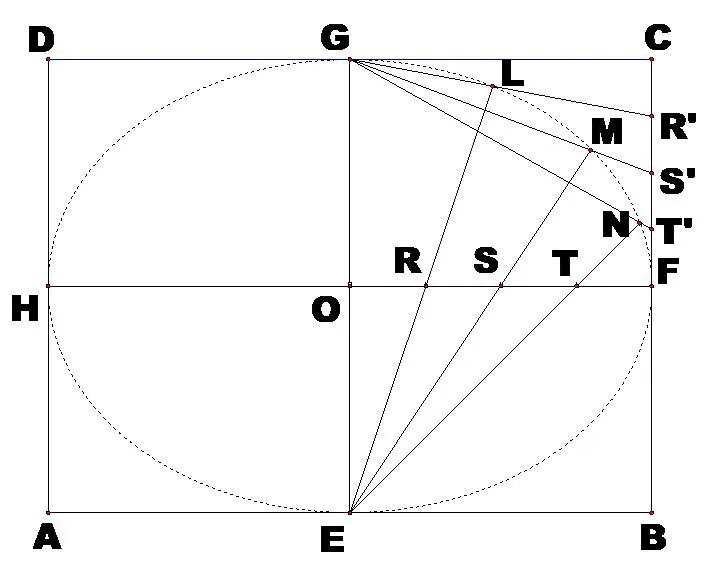
图3

可以预期,随着等分点的增多,构成椭圆的点也在增多,画出的椭圆越精确.论证如下.

二、做法的依据

命题1长方形一组对边的中点与另一组对边中点连线的一半及另一组对边的一半的对应n等分点的连线的交点,在以长方形长、宽为长、短轴的椭圆上.

证明已知长方形ABCD,长、宽分别为2a、2b,建立如图4所示的直角坐标系.将OF、CF分别n等分,记OF的第m个分点为S,CF的第m个分点为S′.连接ES并延长,连接GS′,两线交于点M.则由四点的坐标得直线ES和GS′的方程分别为

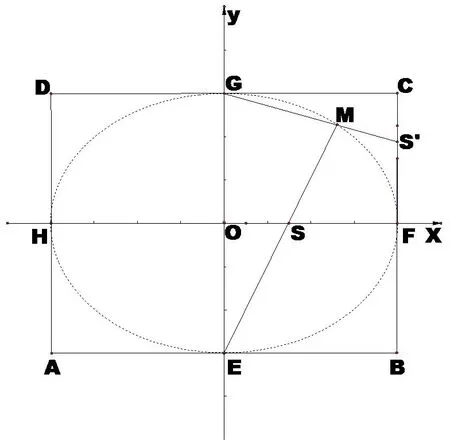
图4

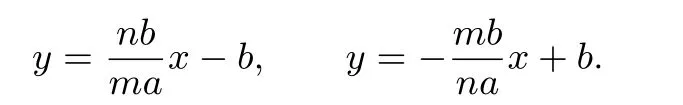
联立以上两个方程,解之得

因此,长方形一组对边的中点(如E、G)与另一组对边中点连线的一半(如OF)及另一组对边的一半(如CF)的对应n等分点 (如S、S′)的连线如 (ES、GS′)的交点 (如M),在以长方形长、宽为长、短轴的椭圆

以上从长方形出发,采用将相关线段等分的方法得到椭圆上的若干个点,这些点形成椭圆的轮廓;但是,这种方法是否可以得到椭圆上所有的点,或者说由椭圆上的任意一点出发,采用上述方法的逆过程是否可以在长方形相应线段上还原出相应的等分点?以下对这个问题做稍微深入的讨论.

三、位于椭圆上的点的一种刻画

命题2椭圆上任一点与某轴的两端点的连线及连线的延长线,截轴和外切长方形的边,所得对应线段之比等于对应两轴之比.(如图5所示,若L在椭圆上,则有.)

证明建立如图5所示的直角坐标系.

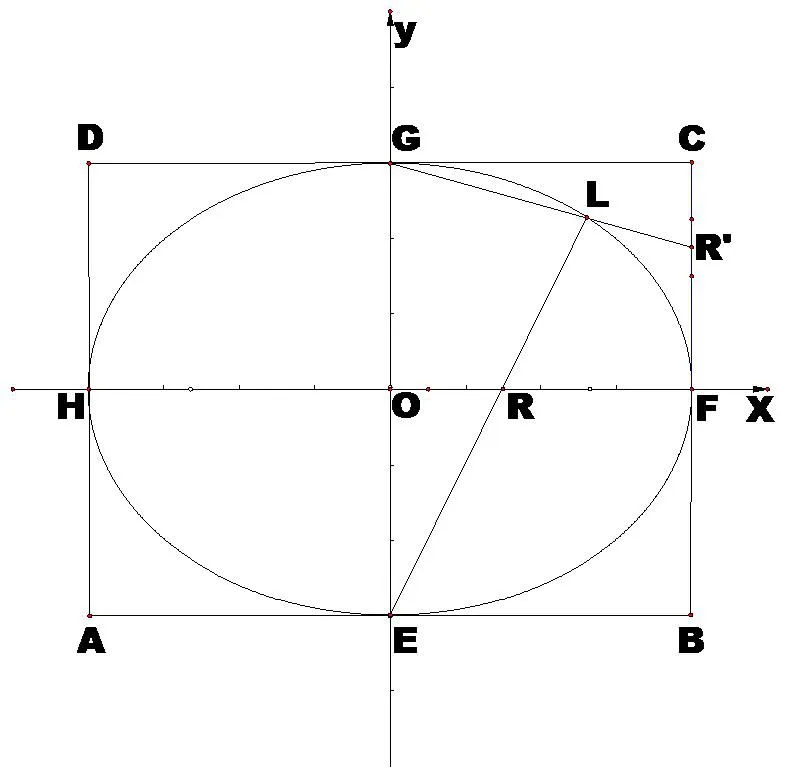
图5

椭圆的长轴HF=2a,短轴EG=2b,分别过E、F、G、H作坐标轴的平行线,四线交于B、C、D、A.则四边形ABCD是长、宽分别为2a,2b的椭圆外切长方形.在椭圆上任取一点L,连接EL交OF于R,连接GL并延长交CF于R′.设直线ER的斜率为k,则它的方程为y=kx−b.联立方程组

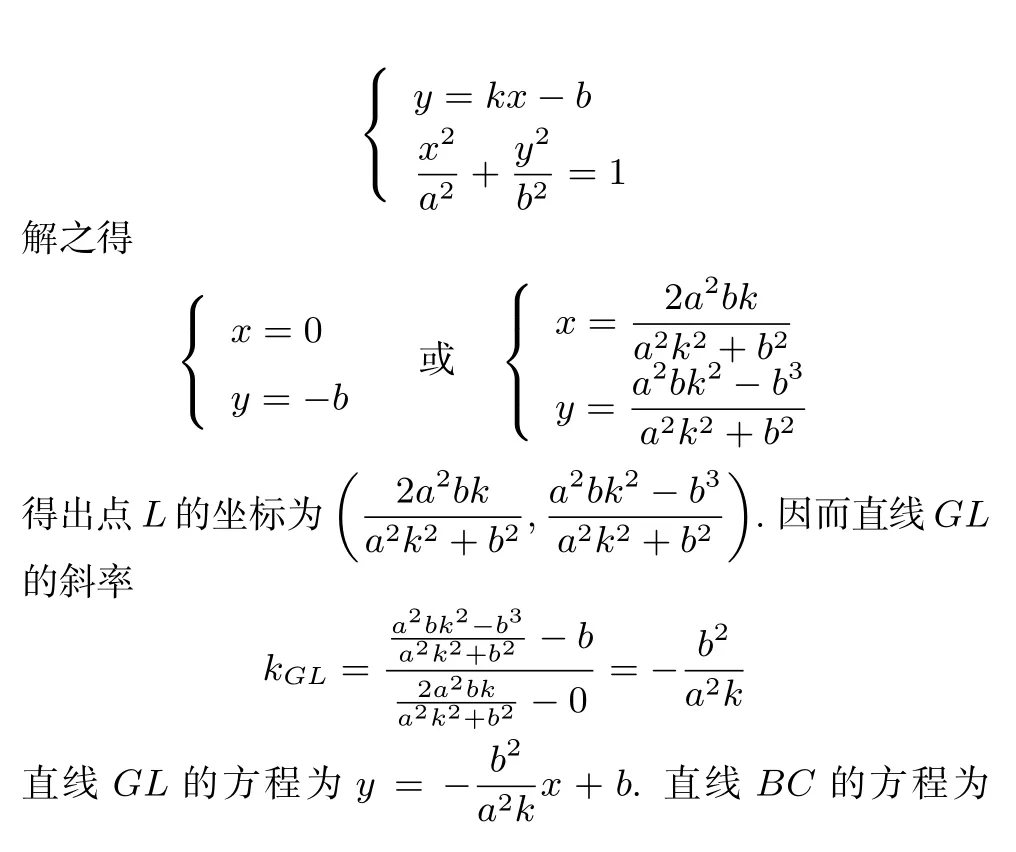
由此可见,利用将相关线段等分的方法得到的是椭圆上的部分点而非全部,因此,椭圆上任意点采用上述方法的逆过程在长方形相应线段上得到的点也不全是等分点.

按照从特殊到一般的认识规律,本文首先给出了在四等分的基础上描点画出椭圆的方法,然后把这种方法推广到任意等分的情况,最后证明了椭圆上任一点与轴的两端点连线及连线的延长线截轴和外切长方形的边所得的对应线段之比等于对应的两轴之比.

我们把上述论证叙述为:长方形ABCD内一点M(x,y),EM交OF于S,GM的延长线交CF于S′,若是定值,则点M的轨迹是一个椭圆(图4).长方形的长是椭圆的长轴长,长方形的宽是椭圆的短轴长,长方形的中心即为椭圆的中心.

[1]刘绍学主编,普通高中课程标准实验教科书,数学选修2-1[M],北京:人民教育出版社,2010.