纯电动汽车传动系统扭振特性灵敏度分析及优化

刘必华 宋田堂 林连华 徐海港 张建武

(1.上海交通大学机械与动力工程学院，上海 200240；2.山东时风(集团)有限责任公司，山东 聊城 252800)

纯电动汽车传动系统扭振特性灵敏度分析及优化

刘必华1宋田堂1林连华2徐海港2张建武1

(1.上海交通大学机械与动力工程学院，上海 200240；2.山东时风(集团)有限责任公司，山东 聊城 252800)

为研究纯电动汽车传动系统的扭振特性问题，首先以某款纯电动汽车为例建立集中质量模型，计算并分析出整车传动系的固有特性和模态振型。其次利用灵敏度分析法，得到了固有频率和振型对惯量和刚度的灵敏度。最后基于灵敏度分析结果，对传动系进行动力学修改，提出优化方案。

纯电动汽车 扭转振动 模态分析 灵敏度分析

0 引言

整车NVH(Noise, Vibration, Harshness)性能一直是汽车设计者关注的重点问题，而传动系统的扭转振动特性对汽车的NVH性能影响很大。与此同时，纯电动汽车作为解决能源枯竭和环境污染的重要手段之一，被广泛推崇。

针对整车的传动系扭转振动研究，国内外专家学者已做了大量工作。邵毅敏等针对轮式车辆传动系进行研究，分析了扭转振动固有特性的灵敏度[1]；向建华等应用系统矩阵法，基于固有特性灵敏度分析对内燃机曲轴扭振系统进行了动力学优化[2]。然而，对于纯电动汽车而言，电机替代了传统的内燃机，使得整个传动系扭振特性发生改变，因此针对纯电动汽车的传动系扭振特性分析显得十分必要。

本文以某款装配两挡自动变速驱动桥的纯电动汽车为研究对象，首先进行了纯电动汽车传动系统的扭转振动分析，利用灵敏度分析手段对传动系统扭振特性进行研究。基于灵敏度分析结果，提出动力学修改方案，使得整车扭转特性得到优化。

1 纯电动汽车传动系统建模

以某纯电动载货车为例，该车配置的电驱动动力总成如图1所示，传动系统主要包括驱动电机、带主减速器的双速变速器、传动半轴和车轮等。

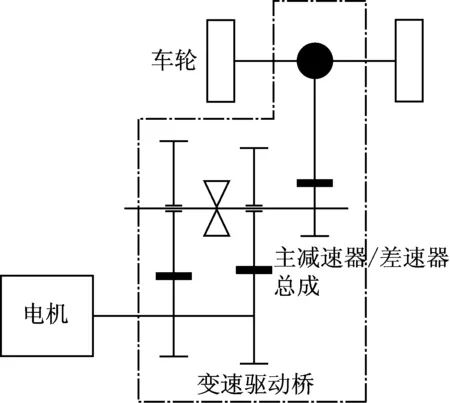
图1 传动系统示意Fig.1 Schematic diagram of the driveline

由于传动系统的质量和弹性分布很不均匀，通常采用多自由度集中质量-弹性-阻尼离散化近似模型，即将实际系统进行参数归一化。只考虑惯性元件的转动惯量和弹性元件的扭转刚度，其中，啮合齿轮副之间的弹性元件的扭转刚度考虑的是齿轮的啮合刚度，其余惯性元件之间的弹性元件的扭转刚度为轴的扭转刚度。该动力传动系统的传动系统扭转振动力学模型如图2所示。

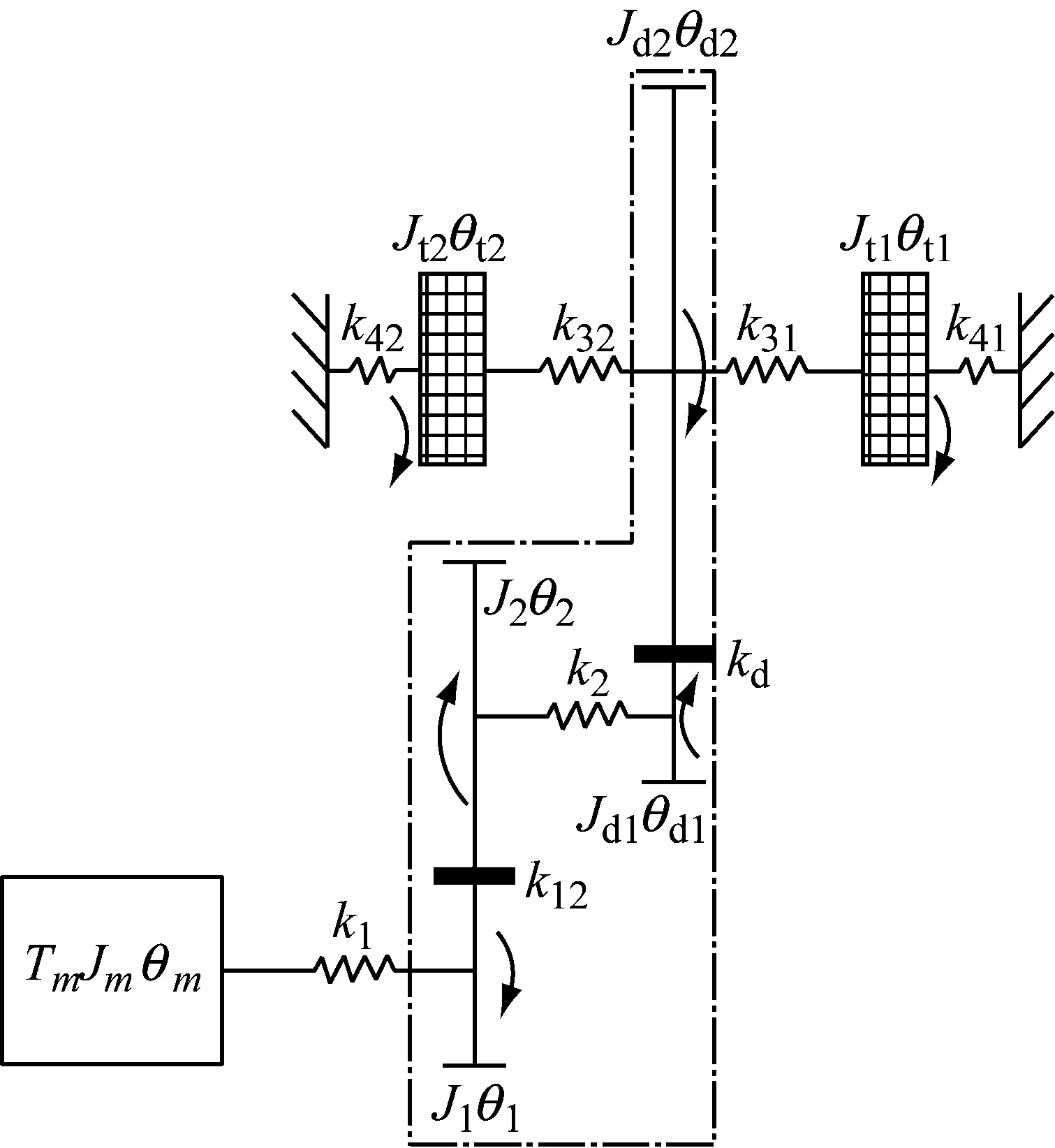
图2 传动系统扭转振动模型Fig.2 Torsional vibration model of driveline

动力从电机Jm开始，通过变速器输入轴k1传递给变速器Ⅰ挡(或Ⅱ挡)齿轮副Jg1、Jg2(Ⅱ挡齿轮副Jg3、Jg4)，并通过传动轴k2传递到主减速器齿轮副Jd1、Jd2，然后分别通过左右半轴传递给左右车轮，最后通过左右车轮传递到地面上，完成动力的传递。其他部件详细参数请见表1、表2和表3。

对图2中扭转振动模型进行等效简化，将左右半轴、左右车轮根据动能守恒的原则进行合并，将整车转动惯量转化到车轮上，从而得到传动系扭振等效模型，如图3所示。

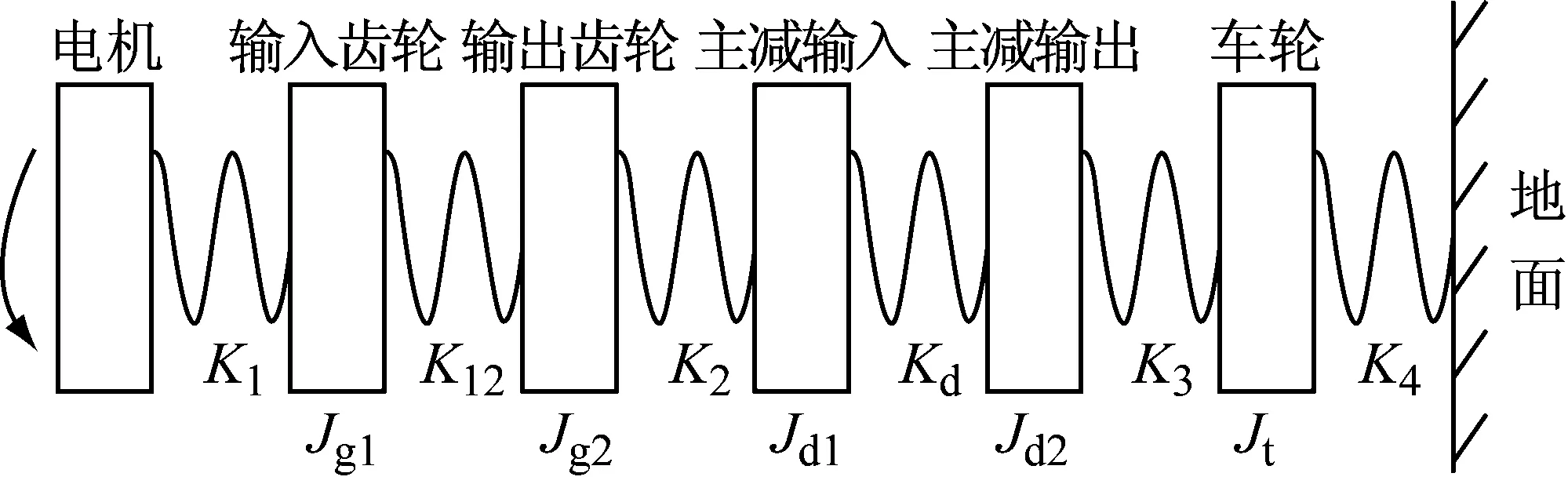
图3 传动系统扭转振动等效模型

序号名称参数值/(kg·m2)1电机Jm0．0472Ⅰ挡主动齿轮Jg10．00013Ⅰ挡被动齿轮Jg20．0025434Ⅱ挡主动齿轮Jg30．0005835Ⅱ挡被动齿轮Jg40．0006416主减速器主动齿轮Jd10．0001077主减速器被动齿轮Jd20．0568车轮Jt0．9159同步器总成J00．00309

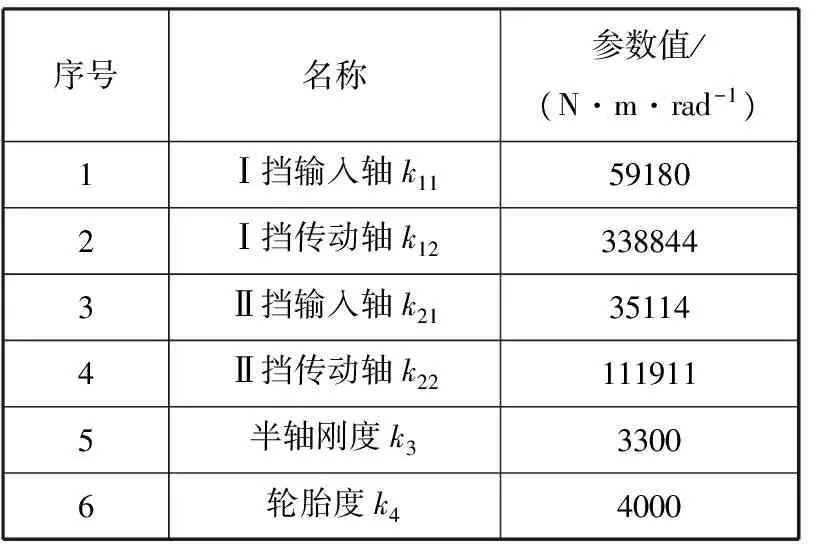
表2 传动系统各部件扭转刚度

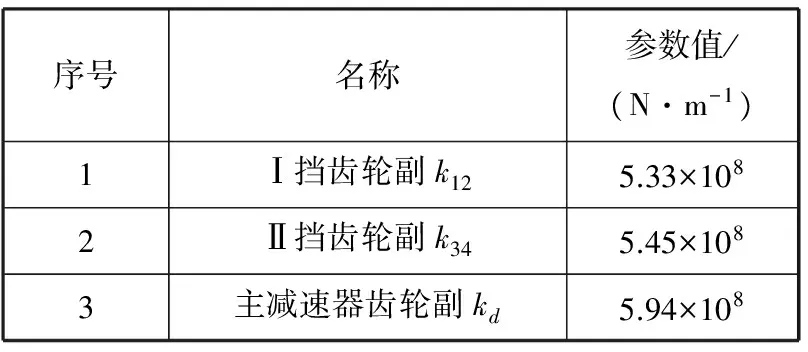
表3 传动系统各部件啮合刚度

2 系统固有特性分析

对于一个当量简化后具有n自由度的系统，扭转振动方程可表达为：

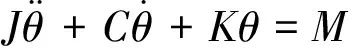
(1)

式中，J、C、K分别为系统的转动惯量矩阵、阻尼矩阵和刚度矩阵，它们均为n×n阶实对称矩阵，且J、K均为正定矩阵；θ为扭转角位移列向量；M为系统的激振力矩列向量。

传动系统的固有模态分析中常不计阻尼，即C=0和M=0，系统的运动方程变为：

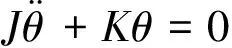
(2)

对式(2)进行实模态分析，可以得到n个特征值及其对应的n个模态向量。

式(2)的特征方程为：

(3)

采用Cholesky三角分解法，将J矩阵分解为2个三角矩阵之积，即：

(4)

将(4)式代入(3)可得：

(5)

令Uθ=φ，则有

(6)

矩阵A=(UT)-1KU-1是实对称矩阵，其特征值λ为原方程的特征值，所求的特征向量φ与系统特征向量θ有关，通过Uθ=φ便可以求得系统特征向量θ。

使用MATLAB求解系统固有模态方程(2)，得到系统的固有频率，各阶固有频率对应的特征向量即为该阶模态振型。在Ⅰ挡和Ⅱ挡时分别计算出的固有频率如表4所示。

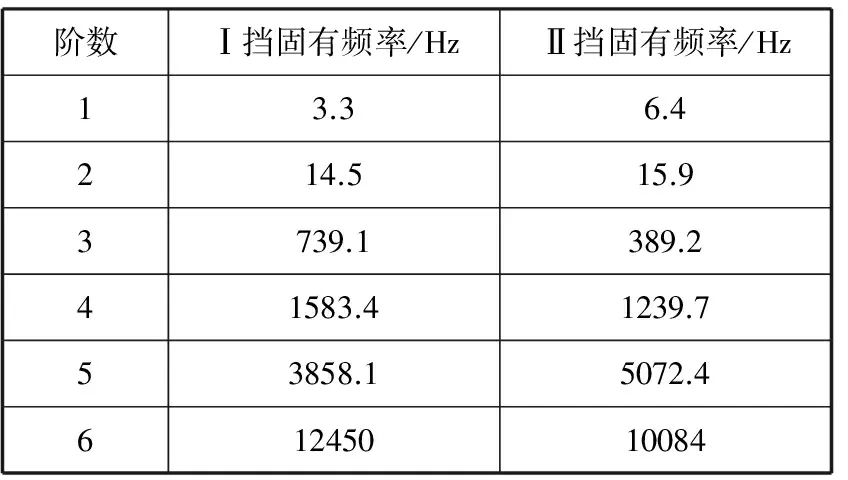
表4 传动系统扭转振动固有频率

将模态振型归一化，去除传动比的影响并整合到同一参考系，得到Ⅰ挡时传动系各阶模态振型如图4所示，Ⅱ挡时传动系各阶模态振型如图5所示。

齿轮传动过程，由于齿轮啮合过程的动态激励会激发传动系的固有模态，因此需要研究齿轮系统的啮合频率的影响。啮频等于轴的转动频率与齿数的乘积：

图4 Ⅰ挡时振型图Fig.4 Mode of vibration at gear Ⅰ

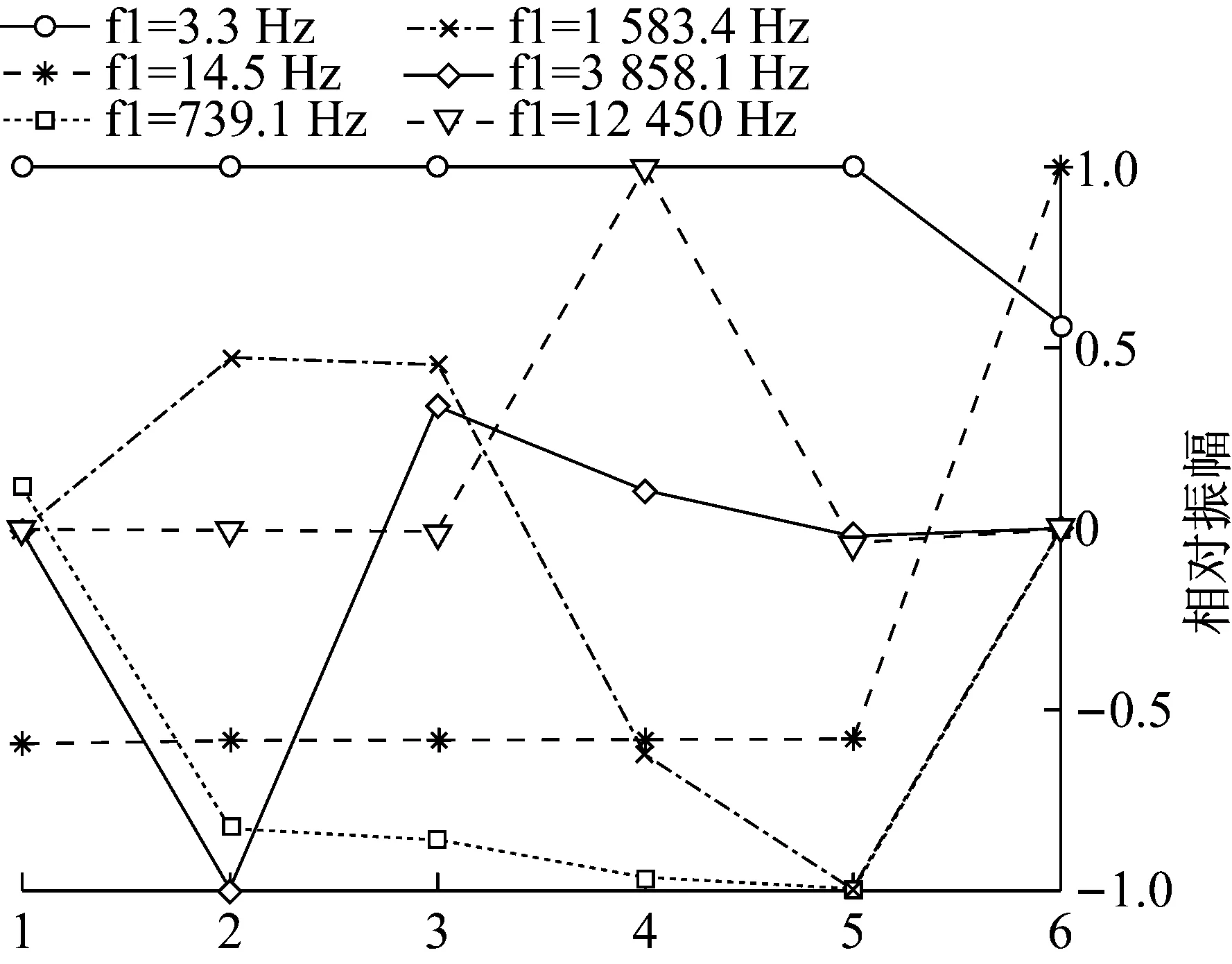
图5 Ⅱ挡时振型图Fig.5 Mode of vibration at gear Ⅱ

(7)

变速器为Ⅰ挡时，电机转速范围为(3000-5500)rpm，Ⅰ挡齿轮啮合频率范围是(1500-2750)Hz，主减速器齿轮啮合频率范围是(360-660)Hz。变速器为Ⅱ挡时，电机转速范围为(3000-6000)rpm，Ⅱ挡齿轮啮合频率范围是(2450-4900)Hz，主减速器齿轮啮合频率范围是(800-1600)Hz。对照以上结果可以看出，传动系第4阶模态可能被激发。

3 固有特性的灵敏度分析

灵敏度分析是研究与分析一个系统的状态对系统参数变化的敏感程度的方法，是运筹学分析中一种很重要的分析方法。灵敏度分析有直接求导法，矩阵摄动发和Nelson法等，其中直接求导法因为物理概念清楚、计算方便而被广泛使用。

令λ=ω2，系统的特征方程为：

(8)

式(7)对结构参数Pm求导，得到特征值对结构参数Pm的一阶灵敏度：

(9)

式中，ωi为第i阶固有频率；θi为第i阶正则化模态向量。本文建立的动力传动系是无阻尼扭振方程，因此结构参数Pm取个质量点的转动惯量和各轴段的扭转刚度。

振型对结构参数Pm的灵敏度有各阶振型的线性组合来表示：

(10)

式中，θk为系统第k阶振型；各阶振型的系数ak通过式(7)求取：

(11)

3.1 固有频率对转动惯量的灵敏度

固有频率对转动惯量求偏导时，扭转刚度视为常数，根据式(8)可得，第i阶固有频率ωi对第j(j=1,2,3…,n)个质量点的转动惯量Mj的灵敏度为

(12)

式中，(θi)j为第i阶振型中的第j个元素。

3.2 固有频率对轴段扭转刚度的灵敏度

固有频率对轴段扭转刚度求偏导时，转动惯量视为常数，根据式(8)可得，第阶固有频率ωi对第j(j=1,2,3…,n-1)个轴段扭转刚度Kj的灵敏度为

(13)

式中，(θi)j为第i阶振型中的第j个元素。

使用MATLAB编程，对传动系统第4阶模态进行灵敏度计算。图6为传动系统第4阶固有频率对系统中各惯量参数的灵敏度，图7为传动系统第4阶固有频率对系统中各轴段扭转刚度的灵敏度。

4 动力学模型优化

可以看到，系统的第4阶固有频率对第二和第四个质量点的转动惯量比较敏感，即Ⅰ挡输入齿轮和主减输入齿轮的转动惯量。同时，系统的第4阶固有频率对第一和第三个轴段扭转刚度比较敏感，即电机输入轴和传动轴刚度。

Ⅰ挡第4阶固有频率为1583.4 Hz，在Ⅰ挡齿轮啮合频率(1500-2750)Hz范围内，可以调小固有频率使其移出啮合频率范围；Ⅱ挡第4阶固有频率为1239.7 Hz，在Ⅱ挡主减速器齿轮啮合频率(800-1600)Hz范围内，可以调大固有频率使其移出啮合频率。经过大量调试发现，改变质量点的转动惯量对固有频率的影响很小，因此选择调整轴段刚度。

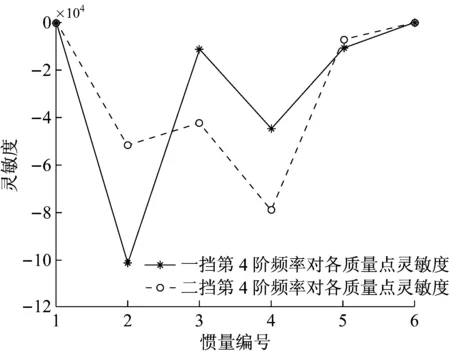
图6 第4阶频率对惯量参数的灵敏度

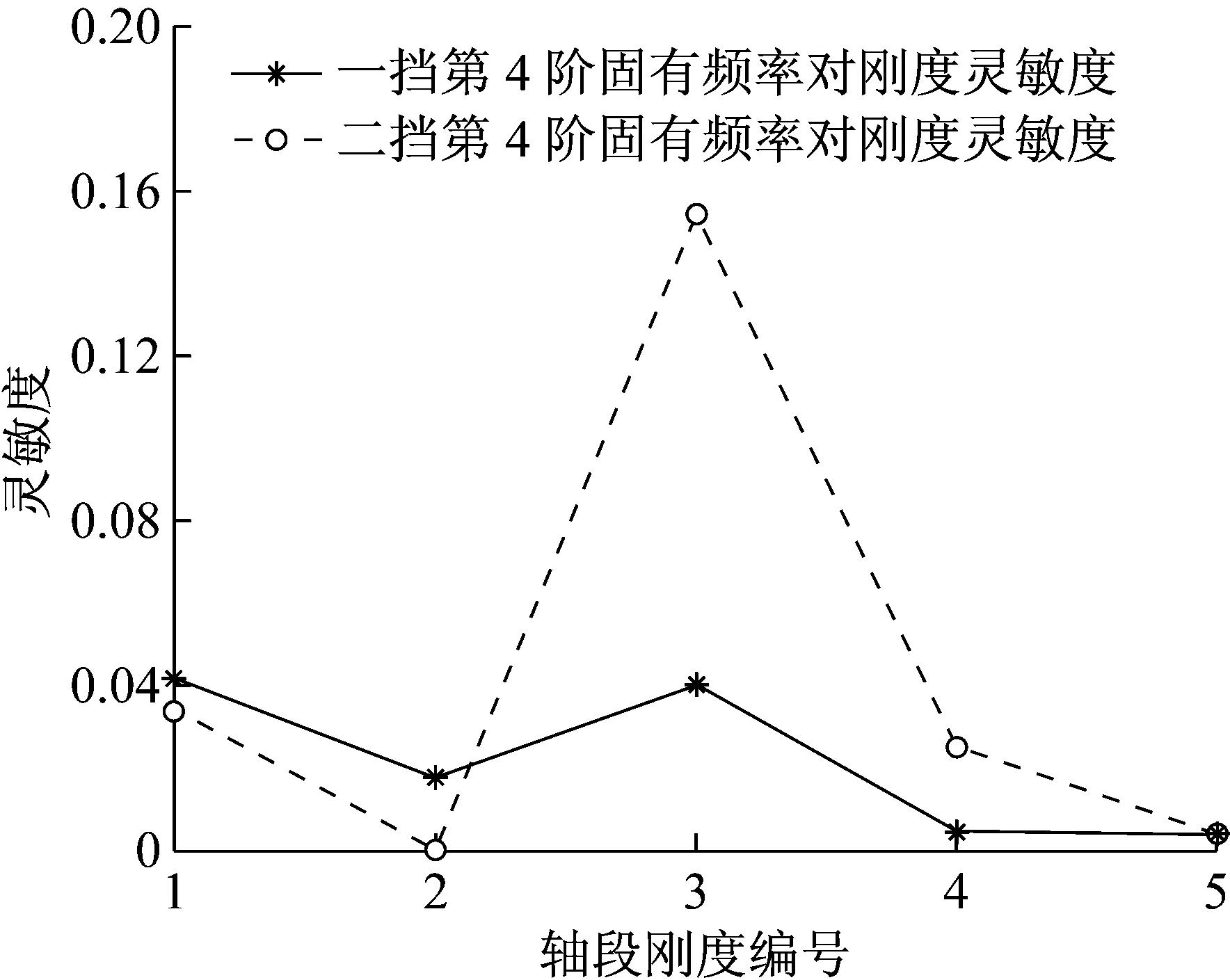
图7 第4阶频率对刚度参数的灵敏度

通过调整现有的变速器齿轮布置位置，如图8所示。将主减速器/差速器总成从Ⅰ挡齿轮侧调整到Ⅱ挡齿轮侧，减小了Ⅰ挡传动轴的扭转刚度的同时，增大了Ⅱ挡时传动轴的扭转刚度，可以有效调整系统的固有频率。

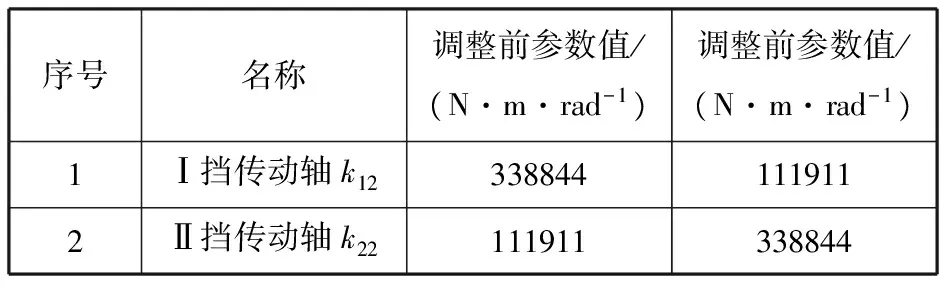
表5 调整后刚度参数

图8 结构调整示意图Fig.8 Diagram of structural adjustment

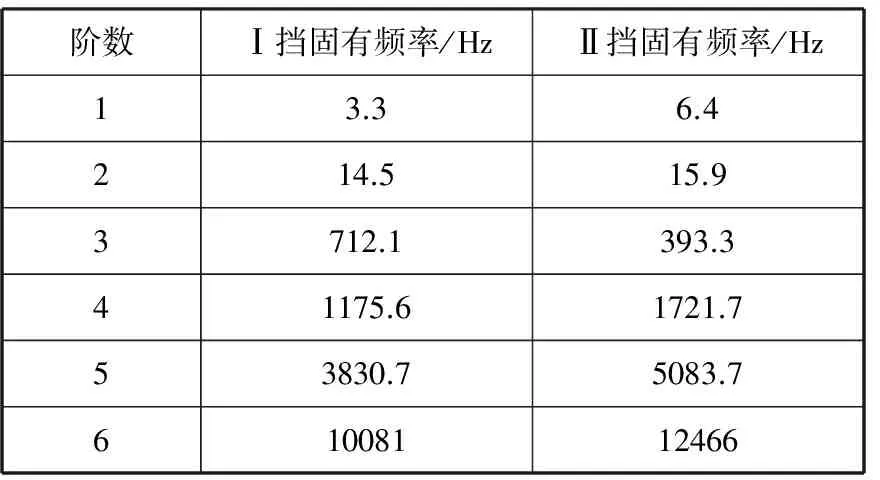
阶数Ⅰ挡固有频率/HzⅡ挡固有频率/Hz13．36．4214．515．93712．1393．341175．61721．753830．75083．761008112466

5 结论

(1)根据传动系灵敏度分析，可以通过调整质量点的转动惯量和扭转刚度来调整模态，但相比较而言，调整刚度相对于调整转动惯量而言效果更加明显。

(2)纯电动汽车传动系在设计初期，可以使用灵敏度分析方法，协助进行参数设计和结构优化，从而避免做实车测试，节省时间和成本。

[1] 邵毅敏，张 奎，李小侠,等.基于灵敏度分析的车辆传动系统扭振分析及仿真[J].长沙理工大学学报(自然科学版),2009,6(3):1-5.

[2] 向建华,廖日东，张卫正,等.基于灵敏度分析的内燃机曲轴扭振系统结构动力学修改[J].内燃机工程(自然科学版),2009,28(6):66-69.

[3] 于 蓬,章 桐.电机驱动车辆动力传动系统建模方法的研究[J]. 佳木斯大学学报(自然科学版),2012,30(4):498-501.

[4] 邹 良, 唐小林, 于海生,等. 混合动力轿车传动系的扭转振动与噪声分析[J]. 汽车工程,2014,36(6):709-714.

[5] 蔡仲昌，刘 辉，项昌乐，曹华夏.车辆行星传动系统扭转振动固有特性及灵敏度分析[J].中国机械工程,22(1):96-101.

[6] 毕金亮，李静波，李宏成，田 雄.动力传动系统扭转模态及灵敏度分析[J].振动工程学报,2010, 23(6):676-680.

[7] 张代胜,王 浩.基于灵敏度分析的汽车动力传动系扭振特性优化[J].中国机械工程,24(5):685-689.

Sensitivity Analysis and Optimization of Torsional Vibration Characteristics of Pure Electric Vehicle Transmission System

LiuBihua1SongTiantang1LinLianhua2XuHaigang2ZhangJianwu1

(1.SchoolofMechanicalEngineering，ShanghaiJiaoTongUniversity，Shanghai200240；2.ShandongShifeng(Group)CompanyLimited，Liaocheng，Shandong252800)

For studying torsional vibration characteristics of electric vehicle, a lumped mass model is established to calculate and analyze the natural frequencies and mode shapes of the driveline. Based on the sensitivity analysis, sensitivity values of natural frequency and vibration mode shapes are calculated. By modifying the most sensitive parameters, a new dynamic structure is given, which proves to be a better choice.

Electric vehicle Torsional vibration Modal analysis Sensitivity analysis

1006-8244(2017)02-003-05

U463.23+4

B

本项目由山东省科技重大专项资助，项目编号2015ZDXX0601C01