目标导向多参考点属性价值模型及评价方法
李春好,李 巍,李孟姣,马慧欣,何 娟,丁丽霞,田 波
(吉林大学管理学院,吉林 长春 130022)
目标导向多参考点属性价值模型及评价方法
李春好,李 巍,李孟姣,马慧欣,何 娟,丁丽霞,田 波
(吉林大学管理学院,吉林 长春 130022)
针对已有规范性决策研究与描述性决策研究尚不能对多参考点共存情形属性价值评价予以全面、直接决策工具支持的不足,通过引入竞争对局及其偏好得分概念提出了基于目标导向效用理论和对局效用比较的新规范性价值函数,在此基础上通过结合范围—频率(RF)理论模型,给出了能够兼顾规范性与描述性两个决策框架的规约性目标导向多参考点属性价值模型及评价方法。相对于规范性目标导向期望价值理论而言,新价值函数在全面科学反映形式多样的决策者偏好结构上具有更为宽广的适用性。相对于RF模型等行为决策理论而言,目标导向多参考点属性价值模型及评价方法克服了行为决策理论模型因其描述性框架性质而不能直接支持决策者属性价值评价的不足,能够对多决策参考点共存情形直接指导决策者的属性价值评价。另外,目标导向多参考点属性价值评价方法将决策目标看成是直接影响方案评价与选择的决策变量,因此也具有发展与深化多属性决策理论的科学价值。模拟验证分析与方法应用表明:目标导向多参考点属性价值评价方法不仅具有广泛的应用适用性,而且在价值评价上也展示出了较强的科学合理性。
属性价值;参考点;目标导向效用;对局效用;范围—频率理论
1 引言
在决策科学领域,学术界基于决策范式(又称为决策框架)将决策理论方法划分为描述性决策(Descriptive Decision Making—DDM)理论、规范性决策(Normative Decision Making—NDM)理论方法和规约性决策(Prescriptive Decision Making —PDM)方法[1-2]。其中,DDM理论旨在解释决策者实际如何选择的决策行为,虽然有时也会给出决策模型,但这类模型并不能直接作为决策的支持工具;NDM理论方法旨在给出的是指导决策者应如何进行理性最优选择的决策工具;PDM方法则是旨在努力克服决策者行为偏见的NDM理论方法应用或是在兼顾决策者应如何选择与实际能如何选择的基础上指导决策者如何选择的程式化方法[1-3]。需要指出,迄今无论相对于上述哪种决策框架而言,价值和效用均是用来反映决策者偏好的常用概念,并且从偏好与属性值之间联系的视角将它们分别称为属性的价值函数和效用函数。从早期文献上看价值和效用这两个概念分别与Bernoulli提出的期望效用模型和 von Neuman和Morgenstern提出的期望效用模型相对应。在Bernoulli模型中,决策者偏好由价值函数予以刻画并且价值函数可通过属性值偏好强度(Strength of Preference)或满意度(Intensity of Satisfaction)的等距判断来测度[1,4];而在von Neuman和Morgenstern模型中决策者偏好由效用函数加以表示并且效用函数的测度所依赖的不是确定性属性值的偏好强度或满意度,而是属性值概率分布不同的两个彩票(又称为前景)之间的优劣选择,由此测度出的效用函数在内涵上讲是一条概率无差异曲线[5]。学术界一般从测度方式上来区分价值(函数)和效用(函数)这两个概念(对应此区分方式应将Bernoulli期望效用模型改称为Bernoulli期望价值模型)。但是,也有不少学者对这两个概念并不予以严格区分,直接将它们称作效用/价值函数,其中一个主要原因在于他们认为属性的价值函数和效用函数之间存在着线性变换关系[2,6]。
迄今关于描述性行为决策,专家学者已提出了多种类型的价值函数或效用/价值函数。例如,对于正向属性(即属性值越大决策者对其偏好也越大的属性)而言,除经典的边际函数值递减的单增价值函数外,前景理论(Prospect Theory)提出者Kahneman和Tversky认为属性价值函数为相对决策参考点(其左侧称为损失区而其右侧称为获得区)的S形单增函数[7-10]。Friedman和Savage认为属性价值函数在低属性值区域为边际函数值递减的单增函数,而在中高属性值区域为S形单增函数[11-12]。Markowitz认为属性价值函数在低属性值区域为边际函数值递增的单增函数,在中等属性值区域为反S形单增函数,而在高属性值区域为边际函数值递减的单增函数[12-13]。虽然有很多学者验证支持Kahneman和Tversky的价值函数,也有不少学者通过实验研究或实证研究对该价值函数予以了反驳,转而验证支持上述其它某种类型的价值函数。例如,Levy和Levy[12]通过心理学实验研究发现至少62%~76%的被试并不具有前景理论的S形价值函数,他们基于实验结果支持的是Markowitz价值函数。如果类似于前景理论将价值函数凹凸性变换的属性值临界点视为决策参考点,那么Friedman和Savage价值函数与Markowitz价值函数便意味着存在着多个参考点影响决策者的属性价值评价。关于多参考点对属性价值的影响作用,有的学者认为每个参考点独立地发挥作用[14];有的学者认为决策者能通过思维将多个参考点整合为一个参考点(等价参考点),整个属性值区间上的价值函数体现为凹凸性仅相对于等价参考点发生一次变化的前景理论价值函数[7]。与至多考虑2~3个参考点同时存在的研究不同,Ordonez等针对很多个参考点同时存在的情景提出可以用Parducci的范围—频率(Range-Frequency—RF)理论(又称为RF模型)对价值形成的行为机理予以解释[14-15]。RF模型认为属性价值由两部分加权构成,其一是相对于属性值范围的范围价值,其二是相对于属性值范围上属性值分布的频率价值。尽管RF模型迄今已为Wedell等[16]、Niedrich等[17]所开展的行为决策研究所证实,但从决策框架上讲它与其它行为模型一样仍属于描述性决策模型,因此并不能直接作为实际决策的支持工具。事实上,即使忽略RF模型的描述性框架性质并用它来指导具体决策,也会遇到模型中的权重无法予以合理赋值的难题(具体原因请见下文)。
尽管行为决策研究在属性价值函数方面已取得了丰富成果,但绝大多数规范性决策研究并没对行为决策领域的相关学术观点予以足够的关注与借鉴,一般只要求决策主体直接判断给出属性值的价值(偏好强度),所给出的模型因此并没有能力解释属性价值的形成机理。作为例外,Bordley等[18-20]实质上基于属性值能否实现决策目标的两水平偏好强度描述框架,提出了一种能够在价值函数上与前景理论具有类似解释能力的规范性决策理论即目标导向效用理论(Target-oriented Utility Theory—ToUT)。ToUT将决策目标视为服从特定概率分布的随机变量,并认为属性价值源于决策目标的概率分布,即属性值的价值是随机决策目标值小于属性值的概率。针对前景理论S形价值函数及其损失厌恶特征(价值函数在参考点处的左导数大于右导数),Bordley等[18]基于目标导向效用理论认为可以采用单峰型决策目标概率分布密度函数及其不对称性予以解释——决策目标累计概率函数的拐点(更准确地说是拐点处的属性值)体现为前景理论价值函数的参考点,参考点处左导数大于右导数的不对称概率密度函数所对应的决策目标累计概率函数在参考点附近会表现出类似于前景理论价值函数的损失厌恶特征。若沿循这种观点,则可以类似地基于目标导向效用理论将已有行为决策研究给出的凹凸性存在多次变化的价值函数,从成因上解释为决策目标概率分布密度函数对应多个参考点所展示出的多峰性。需要指出,尽管目标导向效用理论能够给出上述与相关行为决策研究比较契合的分析结论,但它也有内在缺陷。例如,当决策目标概率分布密度函数无峰时,基于目标导向效用理论人们只能认为决策者的价值函数(即决策目标累计概率函数)无凹凸性变化,而这与事实上没有引入和区分决策目标概率分布的已有大量行为决策实验所给出的研究结论(即价值函数呈现一次或多次凹凸性变化)并不相符。由此看来,人们尚不能仅凭目标导向效用理论将凹凸性存在多次变化的价值函数,简单地归因为决策目标概率分布密度函数对应多个参考点所展示出的多峰性。
现实多属性决策通常以多属性价值技术(Multiple Attribute Value Technique—MAVT[1,4])作为辅助决策工具,其中合理给出决策方案在每个属性上的价值(即决策方案的属性价值),是应用MAVT科学得出方案优劣排序的一个关键所在。有鉴于此,下文在简要介绍和评析目标导向效用理论与RF模型相关要点的基础上,针对规范性决策研究关于价值函数特别是多参考点同时存在情形的价值函数所存在的不足,并考虑到RF模型等关于属性价值的行为决策模型因其描述性框架性质而不能直接用于属性价值评价的事实,首先通过引入竞争对局及其偏好得分概念对目标导向效用理论所采用的偏好强度描述框架予以发展,提出基于目标导向和对局效用比较的新规范性价值函数,然后在承认RF模型所解释出的行为规律基础上,给出一个能够兼顾规范性决策框架与描述性决策框架的规约性目标导向多参考点属性价值模型及评价方法,以为多个决策参考点共存情形下决策者应如何且实际能如何进行属性价值评价提供直接决策支持。其中,共存的多个决策参考点包括属性目标区间的取值端点和一组目标对象所分别拥有的属性值,因此决策者给出属性目标区间以及价值判断所要参照的一组目标对象,是所给模型与方法的决策应用条件。
2 基础理论介绍与评析
(1)目标导向效用(价值)理论
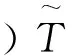
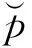
(1)

从本质上看,目标导向效用理论与Bernoulli期望效用模型具有同源性,两者依赖的均是数学中的期望值原理并且在核心概念上使用的均是偏好强度,由此对应价值和效用的一般性概念区分应将ToUT改称为目标导向价值理论(由此下文也将式(1)称为目标导向价值函数)。两者在偏好强度概念使用上的区别主要在于:Bernoulli期望效用模型所依赖的是决策主体对具体属性值所判断给出的、一般说来要随属性值的变化而变化的偏好强度,而目标导向价值理论所依赖的是决策主体对属性值是否实现决策目标值的两水平偏好强度(即偏好得分0和1)。需要指出,两水平偏好强度尽管在现实管理实践上也有类似应用,如足球比赛积分体系将一支球队与其对手比赛的结果即“胜”、“平”与“负”分别记为“3”分、“1”分和“0”分的评分规则,但在同一属性值可实现多个决策目标值时并没有能力区分出决策者对属性值实现较低目标值与实现较高目标值的偏好强度差异。由此,我们并不能简单地基于目标导向价值理论推广Bordley和LiCalzi的有关解释,将已有行为决策研究给出的凹凸性存在多次变化的价值函数,从成因上解释为决策目标概率分布密度函数对应多个参考点所展示出的多峰性。其中具体原因在于:除决策目标概率分布密度函数之外,目标导向价值理论没有区分出的偏好强度差异也可能是解释行为决策研究中价值函数出现凹凸性多次变化的另外一个关键要素。
尽管决策目标随机变量在目标导向价值理论中是一个至关重要的核心概念,但关于该变量所服从的概率分布究竟是客观概率分布还是主观概率分布,现有相关研究并没有予以区分。若将决策目标随机变量所服从的概率分布理解为客观概率分布,虽然可以根除属性效用评价上因决策者而产生的随机误差,并且从决策应用上讲也有利于决策者利用富有针对性的决策信息(如竞争对手的实际分布状况)进行决策,但由于偏好本身是一个主观概念、对于面对同一个决策目标客观概率分布的两个决策者而言他们的属性值价值函数一般说来并不会完全相同,因此从客观概率视角来理解决策目标随机变量的概率分布会使目标导向价值理论出现主客观不一致的逻辑冲突。若将目标导向价值理论中决策目标随机变量所服从的概率分布理解为体现为决策者信念的主观概率分布,则可以使目标导向价值在本质上体现出偏好概念的主观本质。对比上述两方面结论可知:目标导向价值理论仅适用于决策目标随机变量服从主观分布的决策情境。但是,由于主观概率分布毕竟有别于客观概率分布,在能够得知客观概率分布信息的情境下舍弃它转而依赖于即使对于经验丰富的决策者也只能近似反映客观概率分布的主观概率信息,并不是理性决策的最佳选择,因此发展目标导向价值理论、使之能适用于决策目标随机变量服从客观分布的决策情境显然更具有理论价值与实践意义。事实上,若能够通过科学地补充引入除主观概率分布以外的主观因子(如后文引入的用以区分偏好强度差异的对局偏好得分)来发展目标导向价值理论,则不仅能够保证新理论适用于决策目标随机变量服从客观概率分布和主观概率分布的两种决策情境,而且新主观因子的引入也有利于进一步揭示出目标导向价值形成的深层次机理。
(2)RF理论模型
设正向单属性评价问题的被评价对象共有M个,它们对应的属性值最大值和最小值分别记为xmax,xmin,泛指意义上一个被评价对象的属性值记为x,则在Parducci提出的描述性RF模型中,属性值x的价值为:

(2)
其中,vRF(x)称为属性值x相对于属性值范围(Range)[xmin,xmax]的范围价值,其表达式为:
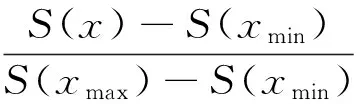
(3)
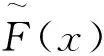

(4)
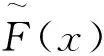
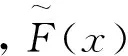
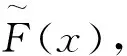
尽管RF模型中权重w的取值一般说来介于0与1之间,但迄今关于该模型的大量实验研究与实证研究表明[15-17,21-22]:w的取值实际介于0与0.5之间。由此,下文规定:0≤w≤0.5。
3 基于目标导向和对局效用比较的规范性价值函数
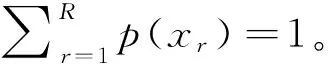
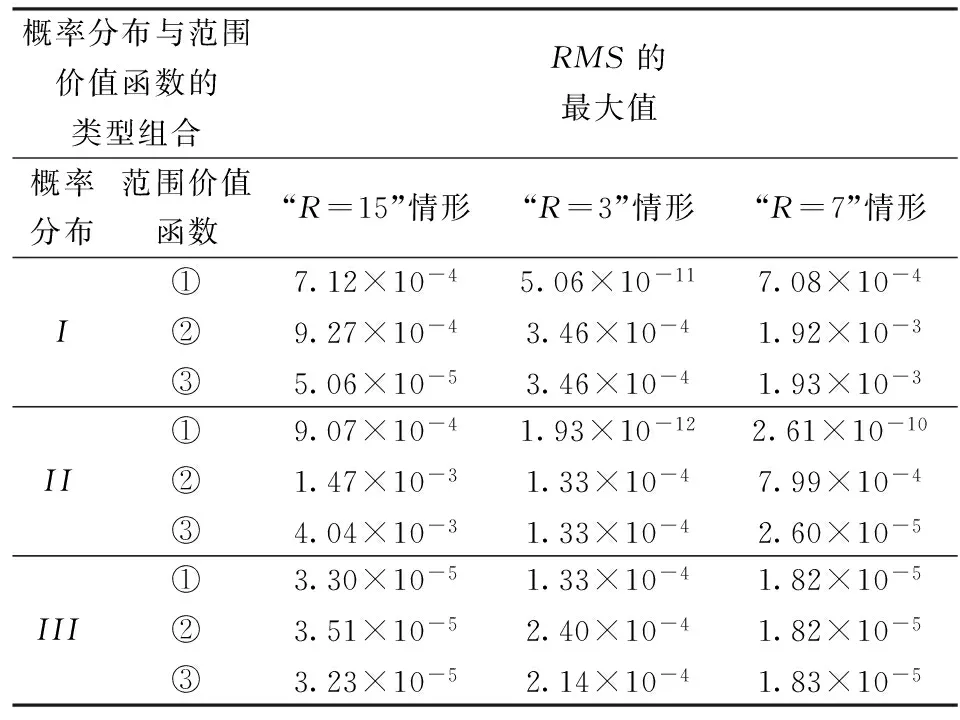
需要补充指出,从实际决策上看无论是对于属性值的客观概率分布还是主观概率分布,若将[xL,xH]等距(或不等距)划分为R个子区间,则这些子区间的中值也可以理解为上面所界定的R个目标对象属性值,相应地可将属性值位于子区间的目标对象占全部对象的频数百分比依次地定义为p(x1),…,p(xR),并且对应这种符号界定总有x1>xL,xR 将属性值为x的待评方案和一个属性值等于xr的目标对象视为竞争对局的双方,并且当x>xr时,我们称属性值为x的待评方案战胜属性值等于xr的目标对象(记作局势〈x>xr〉);类似地,当属性值x=xr时,我们称属性值为x的待评价方案战平属性值等于xr的目标对象(记作局势〈x=xr〉);当属性值x 决策主体是否愿意努力的性格差异也会影响偏好得分δ(xr)、η(xr)。从理性决策上看,若决策主体极其贪图安逸(即努力意愿极低),那么他对δ(xr)-η(xr)随xr的增大所呈现出的变化态势会认为δ(x1)-η(x1)≥…≥δ(xR)-η(xR);若决策主体极其追求卓越(即努力意愿极高),那么会认为δ(x1)-η(x1)≤…≤δ(xR)-η(xR);若决策主体努力意愿体现为中性(或者说体现决策主体是否愿意努力的性格介于极其贪图安逸与极其追求卓越两种性格之间),那么会认为δ(x1)-η(x1)≤…≤δ(xl)-η(xl)≥…≥δ(xR)-η(xR),l∈{2,3,…,R-1}。由此看来,对一位具体的决策者而言其对δ(xr)-η(xr)的变化态势所持有的观点应是下述情形之一: CONSTRAINTS(1): δ(x1)-η(x1)≥…≥δ(xR)-η(xR); CONSTRAINTS(2): δ(x1)-η(x1)≤δ(x2)-η(x2)≥…≥ δ(xR)-η(xR); CONSTRAINTS(R-1): δ(x1)-η(x1)≤…≤δ(xR-1)-η(xR-1)≥ δ(xR)-η(xR); CONSTRAINTS(R): δ(x1)-η(x1)≤…≤δ(xR)-η(xR)。 归纳如上关于δ(xr)、η(xr)的各种关系可知: (5) 利用前述符号规定与偏好得分描述框架,我们可以将属性值等于x(x=xr)的待评价对象表示为对局结果序列: (δ(x1),p(x1);…;δ(xr-1),p(xr-1);η(xr) 属性值等于x>xR的待评价对象的偏好得分为: 归纳上述各式有: v(x)= (6) v(x)从内涵上讲是决策者对“属性值为x的待评方案战胜、战平和不敌各类目标对象”所获满足的数学期望,反映的是决策者对属性值x的偏好强度。由此并沿袭现有决策理论将决策者对确定性属性值的偏好称为价值的习惯,同时考虑到式(6)对目标对象集合的依赖性,我们将v(x)称为以属性值x为自变量、基于目标导向和对局效用比较的价值函数。 对式(6)在[xL,xH]上予以规一化可得: (7) 由于属性值为x的待评价方案战平属性值等于xr的目标对象所反映的实质是x=xr,因此从内涵上讲局势〈x=xr〉的对局偏好得分η(xr)也可以理解为传统意义下决策者对属性值xr的偏好强度。由此并考虑到传统意义下属性值偏好强度的规一化赋值方法(即RF模型中关于vRF(x)的赋值方法),可知η(xr)与vRF(xr)之间存在正线性变换关系,即式(6)与RF模型在输入信息上存在如下对应联系: ∀k=3,…,R。 (8) (9) (10) 令Δ(xk)=δ(xk)/b,Λ(xk)=η(xk)/b,∀k∈{1,…,R}∪{L,H};记 CS(1):Δ(x1)-Λ(x1)≥…≥Δ(xR)-Λ(xR), CS(2):Δ(x1)-Λ(x1)≤Δ(x2)-Λ(x2)≥…≥Δ(xR)-Λ(xR), CS(R-1):Δ(x1)-Λ(x1)≤…≤Δ(xR-1)-Λ(xR-1)≥Δ(xR)-Λ(xR), CS(R):Δ(x1)-Λ(x1)≤…≤Δ(xR)-Λ(xR); 记ε′为正无穷小常数,则可以建立下述线性规划模型: (11) s.t. Λ(xk)≤Δ(xk),k=1,…,R Λ(xk)≤Λ(xk+1),k=1,…,R-1 Δ(xk)≤Δ(xk+1),k=1,…,R-1 Δ(x1)≥ε′>0 CS(l) 0≤w≤0.5 式(11)中,第一组、第二组和第三组约束源于式(10),第四组、第五组、第六组、第七组和第八组约束源于前文关于δ(xr)和η(xr)已给出的数理关系,第九组约束源于前文关于权重w的取值范围规定,第十组约束源于式(8)。此外,由第十组约束可知式(11)的使用条件为R≥3。 δ(xk)=δ*(xk)=bΔ*(xk), η(xk)=η*(xk)=bΛ*(xk), 可以得出: (12) 此外,由w*和RF模型可以得出: x=xk,∀k∈{1,…,R}∪{L,H}。 (13) RMS= (14) 考虑到式(12)以及式(11)对R个目标对象属性值(决策参考点)x1,…,xR的依赖性,我们将式(12)以及式(11)称为目标导向多参考点属性价值模型。 结合前述推导过程,可将目标导向多参考点属性价值评价方法归纳为如下10个步骤。 步骤1:由决策者给出属性值目标区间[xL,xH]。 步骤2:根据统计调查给出或基于决策者信念给出属性值在[xL,xH]上的目标对象集合。 步骤3:依据目标对象集合形成目标对象属性值由小到大的严格排序x1≤…≤xR,并在此基础上通过对目标对象的统计分析给出目标对象属性值的状态概率(客观概率)或由决策者依据其信念给出目标对象属性值的状态概率(主观概率)p(xr),r=1,…,R。 步骤4:若x1>xL且xR 步骤6:请决策者按照传统意义下属性值偏好强度的规一化赋值方法判断给出范围价值vRF(xk),∀k∈{1,…,R}∪{L,H},其中,vRF(xL)=0,vRF(xH)=1。 步骤8:基于式(11)得出Λ*(xk)、Δ*(xk)和w*,k=1,…,R。 需要强调指出,由于式(12)中的Λ*(xk)、Δ*(xk)依赖的是融合描述性决策框架和规范性决策框架的式(11),因此目标导向多参考点属性价值评价方法从决策范式上讲是在兼顾决策者应该如何选择和决策者实际能够如何选择基础上的规约性决策方法。此外,由于式(12)以及其依赖的式(11)并不要求决策者对式(7)中所引入的δ(xr)即局势〈x>xr〉可以获得的对局偏好得分或δ(x1),…,δ(xR)之间的数量关系或δ(xk),η(xk)之间的数量关系予以判断,因此目标导向多参考点属性价值评价方法依赖的决策信息仅是属性值偏好强度vRF(xk)和概率信息p(xk),∀k∈{1,…,R}∪{L,H}。由于概率信息p(xk)在内涵解释为客观概率时可通过统计调查加以获得,在内涵解释为主观概率时可由决策者信念加以给出,而偏好强度vRF(xk)在内涵上是RF理论中的范围价值函数,可按照常用的传统方法(如价值等距判断法)由决策者直接给出,因此从决策信息获取的可行性上讲目标导向多参考点属性价值评价方法与RF理论模型并没有明显差异。但是,与RF理论模型(或前景理论价值模型等)旨在解释决策者实际选择行为但不能作为决策方法工具的描述性决策模型不同,目标导向多参考点属性价值评价方法是一种基于规范性决策框架和决策者实际上能够判断给出或收集给出的决策信息、能直接作为决策工具以指导决策者合理进行属性值价值评价的程式化方法。 (1)模拟验证分析 对应于R=15,设100个目标对象所形成的目标对象属性值严格排序为x1<… vRF(xk)=(xk)Rand1,k=L,1,…,15,H; vRF(xk)= vRF(xk)=(xk)1/Rand1,k=L,1,…,15,H, 其中,Rand1,Rand2分别为取值位于(0,1)、(x1,x15)内的随机数。 针对概率分布类型与范围价值函数类型九种组合(如I与①、III与③等)中的每种组合,随机发生5000组Rand1(或Rand1与Rand2)和目标对象在x1,…,x15上的具体概率值,在此基础上将每组Rand1(或Rand1,Rand2)所对应的vRF(xL),vRF(x1),…,vRF(x15),vRF(xH)以及目标对象在x1,…,x15上的具体概率值带入到式(11)进行求解,得出Λ*(xk)、Δ*(xk)(k=1,…,15)以及w*,之后通过式(12)及RMS指标的计算式,经5000组计算得出了表1第三列所示的模拟统计结果(即RMS的最大值)。 表1 针对每个概率分布与范围价值函数组合各模拟5000次的结果统计 与上述模拟过程类似,对R=3情形(即目标对象属性值严格排序仅有三个数值x1,x2,x3(x3=xR)情形)和R=7情形(即目标对象属性值严格排序有七个数值x1,…,x7(x7=xR)情形)进行仿真模拟,得出的模拟统计结果(即RMS的最大值)如表1第四列和第五列所示。 由表1可知:针对概率分布与范围价值函数的各种类型组合所开展的大量情境模拟,均显示RMS明显小于判断标准0.1。这表明:相对于各种实际决策情境,目标导向多参考点属性价值模型及与之对应的目标导向多参考点属性价值评价方法具有非常广泛的应用适用性。 (2)方法应用 设某教师(视为决策者)要基于数学成绩、外语成绩和专业课成绩三个属性采用多属性价值技术对拟指导的同学甲等几名新入学硕士生(视为备选方案)进行优选。为此,决策者需要对备选方案的数学成绩进行价值(满意度)评价。已知硕士生入学考试数学科目的总分数为150分,考生数学成绩的当年最低入学控制线为85分(视为决策者对数学成绩予以满意度评价的决策参考点),同学甲的数学入学考试成绩为110分。 基于已有关于多属性价值技术的学术文献,决策者可以采用价值等距判断方法进行数学成绩的满意度评价,其中决策者既无需给出目标对象也无需知道目标对象在数学成绩上的状态概率[1,4]。由此并结合决策参考点,我们假定决策者采用价值等距判断方法对新入学硕士生数学考试成绩x给出的主观价值S(x)符合如下仅有一个参考点(即85分)的前景理论价值函数: S(x)=(x-85)0.88,x≥85 (15) 基于该函数可知:决策者对数学成绩85分的满意度为0,并且在规定数学满分成绩150分的满意度为1的条件下,决策者对同学甲数学成绩(110分)所给出的价值评价值(满意度值)为: 由于该值低于满意度区间即[0,1]的中间值0.5,因此结合价值等距判断方法的技术特点可知,无论其他新入学硕士生数学入学成绩怎样分布,决策者对同学甲数学成绩的看法均为“不太满意”。 但是,若在前述信息的基础上决策者得知:除同学甲之外新入学硕士生的数学入学考试成绩分布如表2所示,那么决策者对同学甲数学成绩还会持有“不太满意”看法吗?答案实际是否定的!决策者在这种情况下通常会对同学甲数学成绩感到比较满意甚至很满意(下文将之称为真实定性看法)。 表2 其他新入学硕士生数学成绩在[85,150]上的分布 对比上述目标导向多参考点属性价值评价方法和价值等距判断方法的应用可知:在同学甲数学成绩的价值评价上,前者较之于后者能够得出更接近于决策者真实定性看法的评价结果。 上文首先通过引入竞争对局及其偏好得分概念对目标导向价值理论所采用的偏好强度描述框架予以发展,提出了基于目标导向和对局效用比较的新规范性价值函数,然后在承认RF模型所解释出的行为规律基础上,给出了一个能够兼顾规范性决策框架与描述性决策框架的规约性目标导向多参考点属性价值模型及评价方法。相对于规范性目标导向期望价值理论而言,新规范性价值函数将属性价值的成因由目标导向期望价值理论的单要素说发展为包括决策目标概率分布和(对应多个参考点的)对局偏好得分的两要素说,能够更全面、科学地反映决策者的偏好结构,因此从决策者偏好结构多样性上看具有更为宽广的决策适用性。相对于RF理论模型等关于属性价值的行为决策理论而言,目标导向多参考点属性价值模型及评价方法在借鉴和吸纳RF理论模型有关行为规律的基础上,克服了行为决策理论及模型因其描述性框架性质而不能直接作为决策支持工具指导决策者进行属性价值评价的不足,能够在多决策参考点共存情形下为决策者属性价值评价提供直接的决策支持。综上所述可见,目标导向多参考点属性价值模型及评价方法针对多决策参考点共存情形发展了相关规范性研究成果和描述性研究成果。尽管学术界早已指出确定决策目标、制定备选方案、评价备选方案、选择并实施最优或最满意方案四个决策阶段彼此之间存在相互联系[1,6],但现有多属性决策方法并没有关注决策目标对方案评价与选择的直接影响,仅是把决策目标看成是直接影响备选方案制定并通过制定出的备选方案间接影响方案选择的决策变量。与此不同,目标导向多参考点属性价值评价方法在承认决策目标直接影响备选方案制定的同时,也将决策目标(决策目标集合)看成是直接影响方案评价与选择的决策变量(请参见目标导向多参考点属性价值评价方法的步骤1与步骤2),因此它在决策过程上也具有发展与深化多属性决策理论的科学价值。模拟验证分析与方法应用表明:相对于各种实际决策情境,目标导向多参考点属性价值评价方法不仅具有非常广泛的应用适用性,而且在价值评价上也相对于现有价值等距判断方法展示出了较强的科学合理性。 [1] von Winterfeldt D, Edwards W. Decision analysis and behavioral research[M]. New York: Cambridge University Press,1986. [2] Bell D E, Raiffa H, Tversky A. Decision making:Descriptive, normative, and prescriptive interactions[M]. New York: Cambridge University Press, 1988. [3] French S, Rios I D. Statistical decision theory[M]. New York: Oxford University Press, 2000. [4] Dyer J S, Sarin R K. Measurable multi-attribute value functions[J]. Operations Research, 1979, 27(4): 810-822. [5] Fishburn P C. Utility theory for decision making[M]. New York: Wiley, 1970. [6] Keeney R, Raiffa H. Decisions with multiple objectives: Preferences and value tradeoffs[M]. New York: Cambridge University Press, 1993. [7] Kahneman D, Tversky, A. Prospect theory: An analysis of decision under risk[J]. Econometrica, 1979, 47(2): 263-292. [8] 郝晶晶, 朱建军, 刘思峰. 基于前景理论的多阶段随机多准则决策方法[J]. 中国管理科学, 2015,23(1):73-81. [9] 田丽君,黄海军,许岩. 具有异质参考点的多用户网络均衡模型[J]. 管理科学学报, 2014,17(7):1-9. [10] 樊治平,刘洋,沈荣鉴. 基于前景理论的突发事件应急响应的风险决策方法[J]. 系统工程理论与实践, 2012, 32(5): 977-984. [11] Friedman M, Savage L J. The utility analysis of choices involving risk[J]. Journal of Political Economy, 1948, 56(4): 279-304. [12] Levy M, Levy H. Prospect theory: Much ado about nothing[J]. Management Science, 2002, 48(10): 1334- 1349. [13] Markowitz H M. The utility of wealth[J]. Journal of Political Economy, 1952, 60(2): 151-156. [14] Ordonez L D, Connolly T, Coughlan R. Multiple reference points in satisfaction and fairness assessment[J]. Journal of Behavioral Decision Making, 2000, 13(3): 329-344. [15] Parducci A. Category judgment: A range-frequency model [J]. Psychological Review, 1965, 72(6): 407-418. [16] Wedell D H, Parducci A, Roman D. Student perceptions of fair grading[J]. The American Journal of Psychology, 1989, 102(2): 233-248. [17] Niedrich R W, Weathers D, Hill R C, et al. Specifying price judgments with range-frequency theory in models of brand choice[J]. Journal of Marketing Research, 2009, 46(5): 693-702. [18] Bordley R, Kirkwood F, Craig W. Multi-attribute preference analysis with performance targets[J]. Operations Research, 2004, 52(6): 823-835. [19] Castagnoli E, LiCalzi M. Expected utility without utility[J]. Theory and Decision, 1996, 41(3): 281-301. [20] Brown D B, Giorgi E D, Sim M. Aspirational preferences and their representation by risk measures[J]. Management Science, 2012, 58(11): 2095-2113. [21] Niedrich R W, Sharma S, Wedell D H. Reference price and price perceptions: a comparison of alternative models[J]. Journal of Consumer Research, 2001, 28(3): 339-354. [22] Stewart N, Chater N, Brown G. Decision by sampling[J]. Cognitive Psychology, 2006, 53(1):1-26. [23] Saaty T L. The analytic hierarchy process[M]. New York: McGraw-Hill,1980. Target-oriented Model and Approach for Attribute Value Evaluation with Multiple Reference Points LI Chun-hao, LI Wei, LI Meng-jiao, MA Hui-xin, HE Juan,DING Li-xia,TIAN Bo (School of Management, Jilin University, Changchun 130022, China) attribute value;reference point;target-oriented utility;game utility;range-frequency theory 2016-03-10; 2017-03-06 国家自然科学基金资助项目(71371083);长白山学者特聘教授奖励计划(2014018);吉林大学高峰学科建设项目(2014GSGL) 李春好(1966-),男(汉族),辽宁盖州人,吉林大学管理学院,教授,博士生导师,副院长,管理学博士/博士后,研究方向:评价与决策理论方法,E-mail:jyhlichunhao@126.com.. 1003-207(2017)07-0163-13 10.16381/j.cnki.issn1003-207x.2017.07.018 F224 A


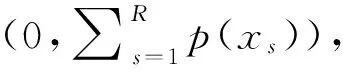
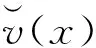
4 属性价值模型及评价方法

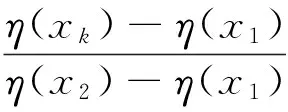
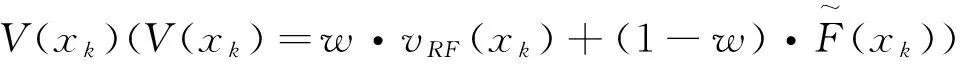



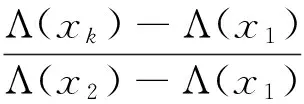


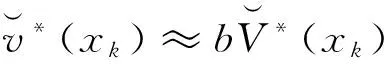

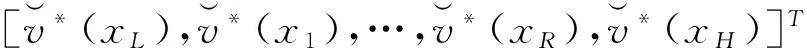


5 模拟验证分析与方法应用


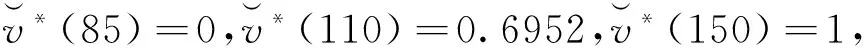
6 结语