考虑投标者有限理性行为的网上临时一口价拍卖的卖方收益分析

高广鑫，樊治平

(1. 南京航空航天大学经济与管理学院，江苏 南京 211106；2.东北大学工商管理学院，辽宁 沈阳 110167)



考虑投标者有限理性行为的网上临时一口价拍卖的卖方收益分析

高广鑫1，樊治平2

(1. 南京航空航天大学经济与管理学院，江苏 南京 211106；2.东北大学工商管理学院，辽宁 沈阳 110167)

网上临时一口价拍卖是一种常见的网上一口价拍卖方式，针对这种方式，在考虑投标者有限理性行为的情形下，如何进行拍卖的卖方收益分析，并在此基础上制定合理的一口价水平，这是一个需要关注的研究课题。在本文中，基于投标者有限理性假设，以完全理性投标者最优投标策略及卖方期望收益模型为研究基础，使用投标者行为选择函数刻画了投标者有限理性行为，并构建了考虑投标者有限理性行为的网上临时一口价拍卖的卖方期望收益模型。进一步地，依据构建的模型，通过一口价水平、投标者人数和投标者有限理性程度对卖方收益影响的数值仿真，以及进行考虑投标者有限理性与完全理性两种情形下的卖方期望收益的比较分析，得到了一些重要结论和管理启示。

网上临时一口价拍卖；有限理性；投标策略；期望收益

1 引言

网上一口价拍卖方式最早于2000年出现在eBay网站上，近年来，其作为一种新兴的拍卖模式已被“淘宝”、Amazon和Yahoo等电子商务网站广泛采用[1]。实践表明，网上一口价拍卖与传统拍卖方式比较，具有明显的经济优势，其有利于分布更广泛的投标者参与竞拍、节省拍卖时间、降低拍卖成本和提高拍卖效率等[2]。随着互联网的发展，越来越多的卖家选择在拍卖网站上发布待出售物品，并通过采用不同的一口价拍卖方式达成交易来获取一定的收益[3]。在主要拍卖网站中，比较常见的一口价拍卖包括三种典型方式：固定一口价、临时一口价和持久一口价拍卖[4]，不同的拍卖网站采用的一口价拍卖方式往往也不相同，即使在同一个拍卖网站中也可能存在不同的一口价拍卖方式[5]。其中，eBay网(www.ebay.com)采用的是临时一口价拍卖[2,6]。临时一口价拍卖的规则，是指当第一位到达拍卖网页的投标者选择参与竞拍时，“一口价”选项功能失效，拍卖过程等同于网上英式拍卖，最高报价者获胜；当第一位投标者选择一口价购买时，拍卖随即结束，其最终支付价格就等于一口价[4,6]。以往的关于临时一口价拍卖的研究[6-8]，大多是在投标者完全理性假设下进行的，然而，在实际拍卖过程中，由于投标者的个体差异、主观因素、掌握信息不完全、不具备较强的信息处理能力等因素，投标者通常会表现出有限理性行为[9-10]，并且投标者的有限理性行为会对卖方最终收益产生影响。因此，在考虑投标者有限理性行为情形下，如何进行临时一口价拍卖的卖方收益分析，这是一个值得关注的研究问题。通过卖方收益分析，有助于卖方选择网上临时一口价拍卖进行在线交易时，科学地设置一口价水平和准确地预测期望收益。

目前，针对考虑投标者有限理性行为的网上临时一口价拍卖的卖方收益研究尚不多见，但可以看到一些相关的研究[3-4,6-8,11-17]。例如：Monderer和Tennenholtz[11]针对网上一口价拍卖中投标者风险态度对于卖方收益的影响进行了研究，他们指出当投标者是风险规避且数量一定时，卖方无论选择何种拍卖方式，其获得的期望收益都不会超过投标者的最高估价，而在投标者风险偏好情形下，卖方的期望收益则将超过投标者的最高估价。Budish等[12]针对网上一口价拍卖中风险中性和风险规避的投标者，分析了最优一口价的设置问题，同时比较了一口价拍卖和英式拍卖的卖方收益；Reynolds和Wooders[7]针对eBay和Yahoo网站采取的网上一口价拍卖的卖方收益问题，分析并比较了投标者风险规避情形下的两种一口价拍卖方式给卖方带来的期望收益，研究表明：Yahoo网采用的一口价拍卖方式会给卖方带来更大的期望收益；杜黎和华桂芬[13]针对同时采用英式拍卖与固定价格拍卖的网上拍卖模式，通过固定价格水平将顾客分为低估价者和高估价者两类投标者，并针对这两类投标者分别研究了其投标行为和卖方的期望收益；倪冠群等[4]针对网上持久一口价拍卖的定价策略确定问题，采用贝叶斯方法研究了投标者出价服从均匀分布情形下的最优一口价制定策略，同时得到一口价的存在会增加卖方期望收益的结论；田剑和高杰[14]针对一口价网上组合拍卖的卖方收益问题，基于独立私人估价模型分别构建了固定一口价组合拍卖和持久一口价组合拍卖的卖方期望收益模型，并且分析比较了两种一口价网上组合拍卖方式给卖方带来的期望收益，研究表明：在拍卖周期内存在估价高于一口价的投标者，且每个投标者的估价均服从[0,1]均匀分布的情形下，卖方采取持久一口价组合拍卖方式获得的期望收益将超过固定一口价组合拍卖；Gallien和Gupta[8]针对网上临时一口价和持久一口价两种拍卖方式，基于投标者到达服从泊松分布且投标时间内生的假设，分别构建了相应的拍卖模型，通过模型求解与比较分析，他们得到结论是：持久一口价拍卖会使得投标者更倾向于做出“最后一分钟投标”决策，在临时一口价拍卖中第一个到达拍卖网页的投标者应该选择立即参与竞拍来使一口价选项失效，而卖方采取持久一口价拍卖获得的收益要超过临时一口价拍卖；Sun等[6]通过假设投标者价值服从一般分布形式且考虑卖方运营成本存在的情形扩展了文献[8]的研究，他们针对固定一口价、纯拍卖和持久一口价三种网上拍卖方式，分别分析了投标者的最优投标策略，并在此基础上，分别构建了三种网上拍卖的卖方期望收益模型，通过对卖方收益的比较分析发现，三种拍卖方式不存在彼此占优关系，卖方在进行网上拍卖方式选择时，需要综合考虑投标者人数、卖方运营成本和投标者参与成本等影响因素；在Sun等[6]的研究基础上，Jiang Zhongzhong等[15]针对考虑投标者有限理性行为的固定一口价、纯拍卖和持久一口价三种网上拍卖方式，基于投标者有限理性的假设，提出了行为选择函数来刻画投标者的有限理性行为，在此基础上，分别构建了三种网上拍卖的卖方期望收益模型，并进一步进行了模型参数的数值仿真，通过理论分析和数值仿真结果发现：基于投标者有限理性的网上拍卖的卖方收益是对投标者完全理性情形下所得结果的一种扩展，且三种网上拍卖方式不存在彼此占优关系，卖方在进行拍卖方式选择时，需要针对每个个案综合考虑影响卖方收益的因素；丁黎黎等[3]基于卖方风险偏好的假设，构建了网上拍卖的卖方拍卖策略的风险回报分析框架，在此框架下，分析了卖方根据其自身的风险容忍度和风险预期设计的拍卖策略带来的收益；杜黎等[16]针对向下降价网上秒杀拍卖模式，分析了投标者的均衡投标策略和卖方的期望收益，在此基础上，比较分析了向上加价秒杀与向下降价秒杀两种拍卖模式下的卖方收益；刘树人等[17]基于供应链库存理论和拍卖理论，分析了联合网上拍卖销售与逆向拍卖采购模式下零售商的拍卖收益和拍卖机制对零售商最优采购策略的影响。

综上，已有成果从不同角度分析了网上拍卖的卖方收益，对于该问题的进一步深入研究奠定了基础。需要指出的是，上述研究大多假设投标者是完全理性的，这意味着，每个投标者总是能够准确地选择实现自身效用最大化的投标策略。然而，在现实拍卖中，投标者通常是有限理性的，即由于心理偏差、认知能力、社会偏好及情感等因素的影响，投标者做出的投标决策往往会系统性地偏差于完全理性假设的结果[9-10]。这样，基于投标者完全理性假设，进行网上一口价拍卖的卖方收益研究具有一定的局限性。虽然Jiang Zhongzhong等[15]研究了考虑投标者有限理性行为的固定一口价、纯拍卖和持久一口价拍卖方式的卖方收益问题，但并未对临时一口价拍卖的卖方收益进行分析。因此，有必要进一步研究考虑投标者有限理性行为的临时一口价拍卖的卖方收益问题。本文是在已有研究的基础上，将投标者完全理性的假设扩展为有限理性的情形。首先针对完全理性投标者在临时一口价拍卖中的最优投标策略进行分析，并给出考虑投标者完全理性情形的临时一口价拍卖的卖方期望收益模型，在此基础上，使用投标者行为选择函数刻画投标者有限理性行为，并构建考虑投标者有限理性行为的临时一口价拍卖的卖方期望收益模型，进一步地，通过一口价水平，投标者人数和投标者有限理性程度对卖方收益影响的数值仿真，分析和比较投标者有限理性与完全理性两种情形下的卖方期望收益，并给出管理启示。

2 基本假设与符号说明

为了针对考虑投标者有限理性行为的网上临时一口价拍卖的卖方收益进行分析，下面分别给出一些基本假设和相关的符号说明。

2.1 基本假设

针对本文研究的问题，这里做出如下前提假设：

1) 在拍卖过程中，针对不可分割的单物品拍卖，到达拍卖网页的投标者数量为n,n>1,且允许每个投标者多次提交报价。

2)每个到达拍卖网页的投标者参与一口价拍卖的成本相同，且他们在进行投标策略(以一口价直接购买、参与竞拍或离开拍卖网页)选择时，均将做出有限理性决策。

3)独立私人估价假设，即每个投标者都知道自己的估价v,但其他投标者不了解其估价且每个投标者的私人估价不受其他投标者估价的影响，且v服从区间[0,vmax](vmax≤1)上的分布，分布函数为F(v),其中，F(0)=0,F(vmax)=1,密度函数为f(v)。这些信息为买卖双方的共同知识，所有投标者之间是对称的。

4)如果标的物以竞拍方式成交，则采用第2价格密封式拍卖(Vickrey拍卖)方式来确定最终成交价，即投标者按照自己的真实估价进行投标是占优策略[18]。

5)如果拍卖结束时，标的物没有成交，则卖方会产生非负的运营成本，即监督网上拍卖过程产生的每次投标成本或下一时期在网上重新发布该产品的额外费用[6]。

基于上述假设可知，每一个投标者都有自身对于拍卖物品的真实估价，同时投标者不知道他人的具体估价，但是投标者之间都知道彼此估价的概率分布，投标者的估价相互独立且存在差异是投标者们的价值观差别的实际体现[4]；若标的物通过竞拍方式成交，采用Vickrey拍卖来确定最终成交价，则能够有效反映主要拍卖网站中顾客的投标行为(如狙击投标等)[19]，这与实际网上拍卖相符合。

2.2 符号说明

为了便于下文分析，本文涉及的相关符号及变量的含义描述如下：

n投标者人数(潜在竞买人数量);F(v)投标者估价分布函数;f(v)投标者估价概率密度函数;Ai第i个到达拍卖网页的投标者,其中i=1,2,…,n;vi第i个投标者估价;vmaxn个投标者估价的最大值;X(n,i)n个投标者中第i大的投标者估价;G(n,i)(v)X(n,i)≤v的概率,其中G(n,i)(v)=∑i-1j=0Cjn[1-F(v)]j[F(v)]n-j,i=1,2,…,n;g(n,i)(v)G(n,i)(v)的概率密度函数,其中g(n,i)(v)=i/[1-F(v)]Cin[1-F(v)]i[F(v)]n-if(v),i=1,2,…,n;v-投标者选择参与竞拍阈值;v-投标者以一口价购买阈值,且v-≥v-;w投标者参与一口价拍卖的成本;h卖方单位物品运营成本;πrt考虑投标者完全理性情形下,卖方选择临时一口价拍卖获得的期望收益;πbrt考虑投标者有限理性情形下,卖方选择临时一口价拍卖获得的期望收益;Ut投标者从临时一口价拍卖中获得的期望效用;pa获胜投标者支付的价格;pb卖方设置的一口价;ψ有限理性投标者选择参与竞拍的概率;β投标者有限理性行为参数;α行为选择函数曲线的曲率系数。

3 考虑投标者完全理性情形的临时一口价拍卖的卖方期望收益模型

为了便于进行考虑投标者有限理性行为的网上临时一口价拍卖的卖方收益分析，需要以考虑投标者完全理性情形的卖方收益研究为基础，为此，这里首先给出完全理性投标者的最优投标策略分析，然后在此基础上构建考虑投标者完全理性情形的临时一口价拍卖的卖方期望收益模型。

3.1 完全理性投标者的最优投标策略

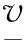
(1)

(2)

由式(2)可得：

(3)

Ut=v1-pb

(4)

(5)

将式(3)代入式(5)，可得：

(6)

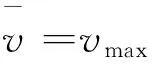
(7)

(8)

3.2 临时一口价拍卖的卖方期望收益模型

基于上述对完全理性投标者参与临时一口价拍卖的投标策略分析，可进一步给出投标者完全理性情形下临时一口价拍卖的卖方期望收益模型构建过程的描述：

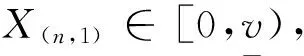
通过上述分析，可构建考虑投标者完全理性情形的临时一口价拍卖的卖方期望收益模型如下：

(9)

4 考虑投标者有限理性行为的临时一口价拍卖的卖方期望收益模型

实际的网上临时一口价拍卖是一个复杂的随机环境，它通常涉及多个带有不同动机和理性程度的投标者，每个投标者据此选择的投标策略都是因人而异且复杂多变的，并且其将对卖方的最终收益产生影响[8]。为了分析考虑投标者有限理性行为的卖方期望收益，下面分别给出投标者有限理性行为刻画和卖方期望收益模型构建的描述。

4.1 投标者有限理性行为刻画

网上拍卖是一个复杂不确定的环境，投标者拥有的信息是不完全的，其行为通常会受制于个人心理偏见、投标经验或认知上的约束[20-22]，并且不具备较强的信息处理能力，很难计算得到参与竞拍阈值和一口价购买阈值，从而无法做出在完全理性假设下的最优投标决策，也就是说，投标者在拍卖过程中往往表现出有限理性行为[23-24]。由于投标者在临时一口价拍卖与持久一口价拍卖中的投标策略相同[6]，因此，这里可考虑采用Jiang Zhongzhong等[15]针对持久一口价拍卖构建的基于投标概率的行为选择函数来刻画投标者的有限理性行为特征，即:

(10)

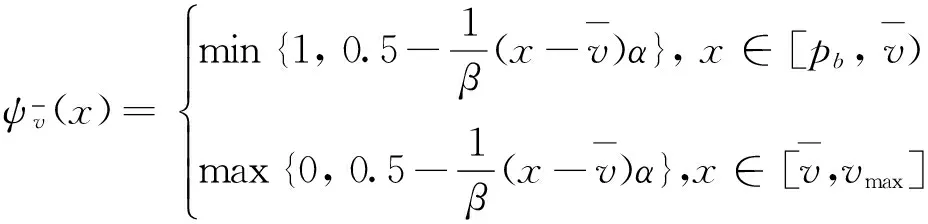
(11)

其中，β表示投标者的有限理性程度，β∈(0,∞),且β越大，表示投标者的有限理性程度越大；α表示行为选择函数曲线的曲率系数，且α=1/(2k+1)或

(12)

(13)

在这种情况下，投标者会做出最优投标策略的选择，这与3.1节关于完全理性投标者最优投标策略的分析相符合。因此，考虑投标者完全理性情形的投标策略选择行为是考虑投标者有限理性情形的投标策略选择行为的一个特例。

4.2 临时一口价拍卖的卖方期望收益模型

基于考虑投标者完全理性情形的临时一口价拍卖的卖方期望收益模型，以及有限理性投标者投标行为选择函数，下面给出考虑投标者有限理性行为的临时一口价拍卖的卖方期望收益模型构建过程的描述。

在临时一口价拍卖中，当没有投标者选择参与竞拍或者以一口价直接购买时，即n个投标者均选择离开拍卖网页时，标的物没有成交。此时，卖方的期望收益为一个负的运营成本，即:

(14)

在临时一口价拍卖中，当投标者A1选择参与竞拍时，“一口价购买”选项消失，临时一口价拍卖转化为网上二级价格密封式拍卖，最高报价者获胜，支付价格为次高报价。此时，卖方的期望收益为次高价的期望，即:

(15)

在临时一口价拍卖中，当投标者A1选择以一口价直接购买时，整个拍卖过程结束。此时，卖方期望收益为设定的一口价，即:

(16)

综上三种情况分析，考虑投标者有限理性行为的临时一口价拍卖的卖方期望收益模型可由下式表示：

(17)

5 数值实验

基于上述考虑投标者完全理性与有限理性情形的网上临时一口价拍卖的卖方期望收益模型，为了分析说明模型参数对卖方收益的影响，下面分别给出一口价水平、投标者人数和投标者有限理性程度三个因素在固定卖方运营成本、投标者参与成本与曲线曲率系数情形下的数值仿真过程，这里参考文献[6]和[15]中相关参数取值，假设投标者的估价vi服从[0,1]均匀分布，卖方运营成本h=0.02,投标者参与一口价拍卖成本w=0.02,行为选择函数曲线的曲率系数α=1。同时，在数值仿真过程中，参考文献[15]给定其他参数取值范围。在此基础上，通过数值仿真分析上述三个因素对考虑投标者完全理性与有限理性情形的卖方收益影响，并且对上述两种情形的卖方收益进行分析和比较，此外，依据数值仿真结果，进一步给出相关的管理启示。

5.1 一口价水平对卖方收益的影响

根据上述分析可知：在实际网上拍卖中，当卖方设置的一口价水平较低且预期潜在投标者人数较多时，则其可以优先考虑选择临时一口价拍卖方式，因为这种拍卖方式可能会给卖方带来超过最大一口价水平的期望收益；对于卖方而言，一口价不宜设置过低，否则投标者总是选择以一口价成交，使得卖方收益降低，也不宜过高，否则投标者总是选择参与拍卖，失去一口价的应有作用，同时也会使卖方收益受损。

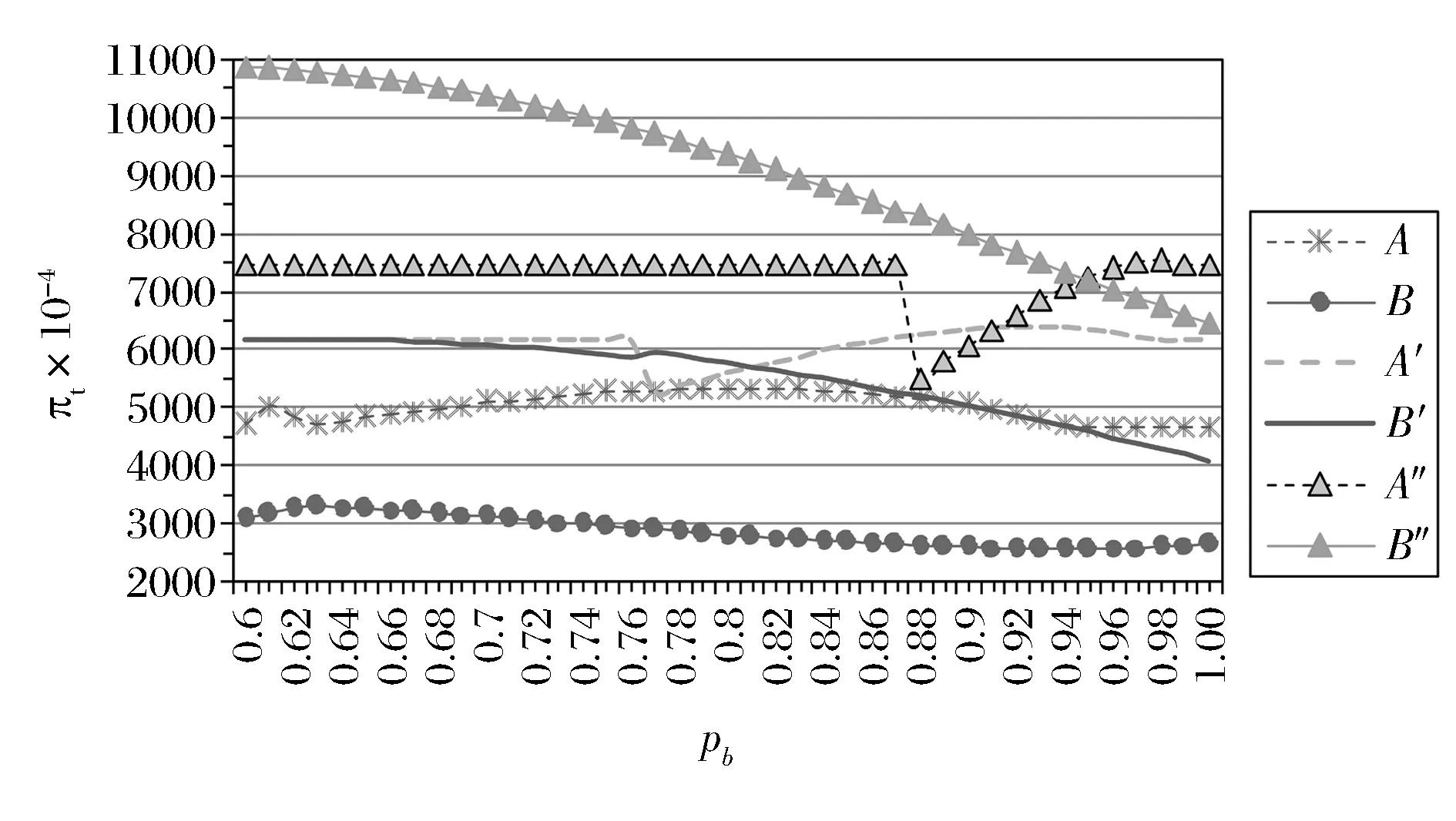
注：A,A ′和A ″分别表示n=3,n=5和n=10三种情况下随pb的变化趋势；B,B ′和B ″分别表示n=3,n=5和n=10三种情况下随pb的变化趋势。图1 一口价水平pb对卖方期望收益和的影响

5.2 投标者人数对卖方收益的影响

根据上述分析可知：在实际网上临时一口价拍卖中，如果拍卖物品吸引到的投标者人数越多，那么该拍卖品成交的可能性就越大，且卖方收益会随之增加；如果卖方设置的一口价水平适中，且拍卖物品可以吸引到较多的具有较高有限理性程度的投标者时(如青年顾客)，则卖方期望收益将增加。

注：A,A ′和A ″分别表示(β,pb)=(5,0.85),(β,pb)=(10,0.85)和(β,pb)=(10,0.9)三种情况下随n的变化趋势；B,B ′和B ″分别表示(β,pb)=(5,0.85),(β,pb)=(10,0.85)和(β,pb)=(10,0.9)三种情况下随pb的变化趋势。图2 投标者人数n对卖方期望收益和的影响

5.3 投标者有限理性程度对卖方收益的影响

根据上述分析可知：在考虑投标者有限理性行为的网上临时一口价拍卖中，当预期参与拍卖的投标者人数一定且预期投标者有限理性程度不会很低时，通常设置较低的一口价，会使得卖方得到较大的期望收益；当一口价水平被设定后，预期参与拍卖的投标者人数越多且投标者的有限理性程度不会太低时，卖方得到的期望收益越大。

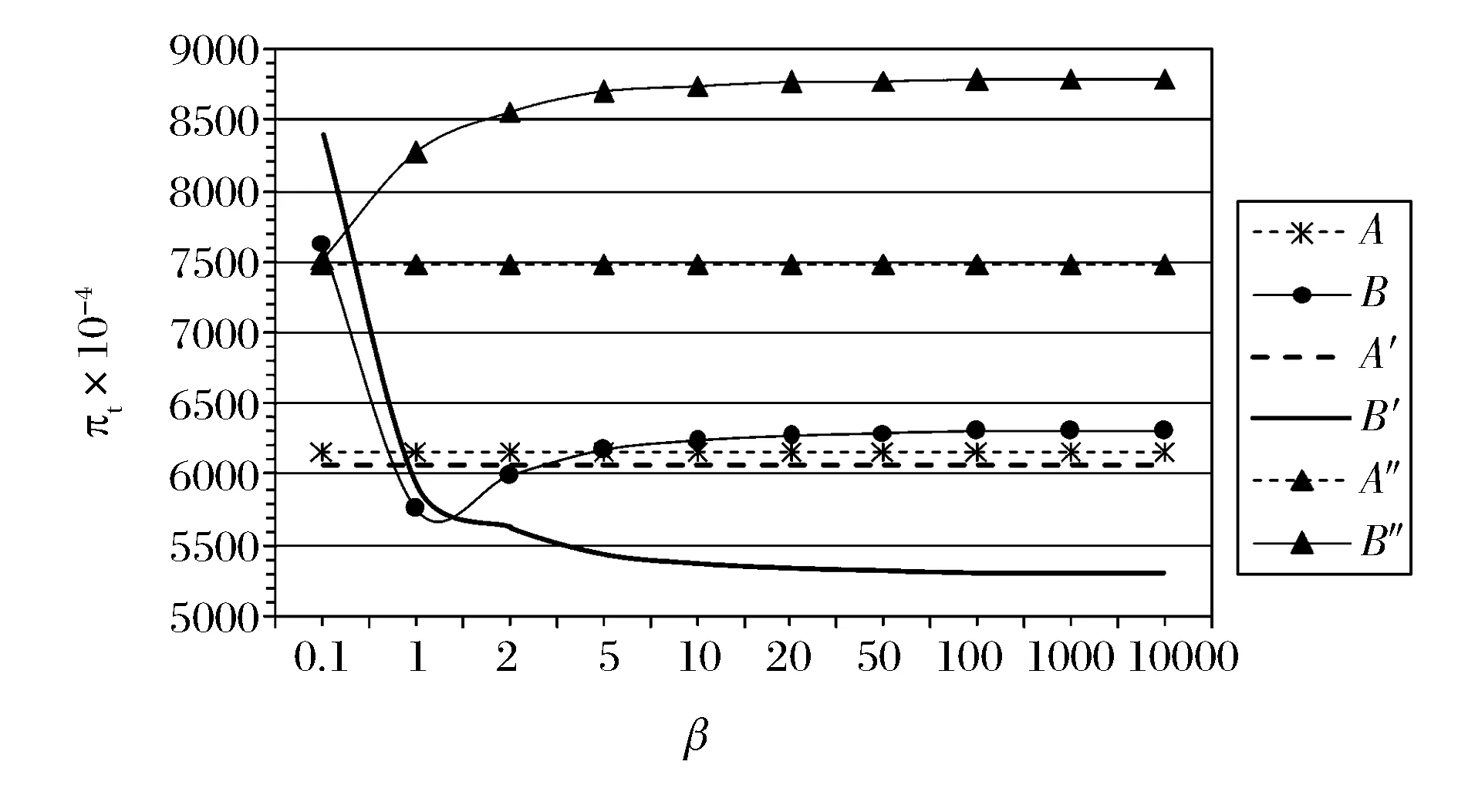
注：A,A ′和A ″分别表示(n,pb)=(5,0.65),(n,pb)=(5,0.85)和(n,pb)=(10,0.85)三种情况下随β的变化趋势；B,B ′和B ″分别表示(n,pb)=(5,0.65),(n,pb)=(5,0.85)和(n,pb)=(10,0.85)三种情况下随β的变化趋势。图3 投标者有限理性程度β对卖方期望收益和的影响

6 算例分析

本节通过一个算例分析来说明上文构建模型的潜在应用以及可行性和有效性。这里，以二手商品网上临时一口价拍卖为例，测算考虑投标者有限理性心理行为与投标者完全理性两种情形下的卖方期望收益，并进行相应的比较分析。

考虑eBay网某注册用户，准备采用网上临时一口价拍卖方式将个人闲置的二手自行车进行在线交易。该用户(卖方)通过对主要拍卖网站上有限的历史数据的统计，发现大多数挂在拍卖网站上的同款自行车价格都设置在0.6千元至1千元之间，参与竞拍的顾客(投标者)人数从3人至13人不等，且参与竞拍的顾客的结构以青年人为主，拍卖持续时间从7天至30天不等，卖方的平均运营成本为h=0.02千元，每个投标者参与竞拍的平均成本为w=0.02千元。在参考网上相关拍卖信息后，该卖方通过自身对标的自行车的估价，考虑可将拍卖一口价设置为pb=0.85或0.9千元。为了便于使用上文构建的网上临时一口价拍卖的卖方期望收益模型进行拍卖收益测算，对模型中的参数作如下设定：投标者对拍卖品的估价vi服从[0,1]上的均匀分布，投标者的估价最大值vmax=1,投标者行为选择函数曲线的曲率系数α=1,同时假设以青年人为主的顾客是具有较高有限理性程度的投标者群体，可设β≥5。

表1 针对三个参数(pb,n,β)不同组合的和计算结果

7 结语

本文以完全理性投标者的最优投标策略及卖方期望收益模型为研究基础，构建了考虑投标者有限理性行为的网上临时一口价拍卖的卖方期望收益模型，基于该模型，通过相关理论分析和数值仿真，可以得到如下结论：

1)在网上临时一口价拍卖中，投标者的有限理性行为对于卖方收益具有重要的影响，与完全理性投标者相比较，有限理性投标者可以使得卖方从临时一口价拍卖中获得更大的期望收益，特别当参与拍卖的投标者人数较多且卖方设置较低的一口价时。

2) 在考虑有限理性投标者参与的网上拍卖中，当卖方设置较低的一口价且预期潜在投标者人数较多时，由于这种拍卖方式可能会给卖方带来超过最大一口价水平的期望收益，则其可以优先考虑选择临时一口价拍卖方式进行在线交易。

3)在网上临时一口价拍卖的卖方收益分析中，综合考虑多个影响因素(如一口价水平、投标者人数、投标者有限理性程度、卖方运营成本、投标者参与成本等)是有必要的，这些因素将对卖方期望收益产生影响。

基于本文研究的结论，得到关于网上临时一口价拍卖实践的若干管理启示如下：

1)在网上临时一口价拍卖中，卖方对于一口价不宜设置过低，否则投标者总是选择以一口价成交，使得卖方收益降低；同时一口价也不宜设置过高，否则投标者总是选择参与拍卖，失去一口价的应有作用，也会使卖方收益受损。

2) 如果某拍卖物品吸引到的投标者人数越多，那么该拍卖物品成交的可能性就越大，且卖方收益会随之增加；如果卖方设置的一口价水平适中，且拍卖物品可以吸引到较多的具有较高有限理性程度的投标者(如以青年人为主的投标者)时，则卖方期望收益将增加。

3) 当投标者人数一定且预期投标者有限理性程度不会很低时，通常设置较低的一口价，会使得卖方得到较大的期望收益；当一口价水平被设定后，预期参与拍卖的投标者人数越多且投标者的有限理性程度不会太低时，卖方得到的期望收益越大。

与已有研究相比，本文的主要贡献在于：

1)针对网上临时一口价拍卖，采用已有的基于投标概率的投标者行为选择函数刻画了投标者有限理性行为。

2)将投标者有限理性行为与在线拍卖理论相结合，针对网上临时一口价拍卖形式，构建了考虑投标者有限理性行为的卖方期望收益模型，扩展了传统的基于投标者完全理性假设的在线拍卖理论的相关研究，同时为拍卖者在现实中测算在线拍卖收益提供了理论支持。

3)通过对投标者有限理性行为、一口价水平和投标者人数对卖方期望收益的影响分析，所得出的管理启示为拍卖者采用网上临时一口价拍卖进行在线交易提供了参考依据。

未来需要研究的问题是：考虑投标者参与成本随其到达时间变化情形下，有限理性投标者参与的多物品网上临时一口价拍卖的卖方收益问题。

[1] 杨兴丽, 陈霞, 吕廷杰. 网上一口价拍卖顾客投标策略研究[J]. 管理科学, 2007, 20(4): 57-60.

[2] 陈剑, 陈熙龙, 宋西平. 拍卖理论与网上拍卖[M]. 北京: 清华大学出版社, 2005.

[3] 丁黎黎, 徐寅峰, 刘新民. 基于风险偏好下的网上在线拍卖策略设计[J]. 中国管理科学, 2014, 22(3): 96-102.

[4] 倪冠群, 徐寅峰, 郑斐峰. 网上一口价在线拍卖的定价策略设计[J]. 管理科学学报, 2011, 14(3): 1-9.

[5] Zoltan H, Wang Wenli, Whinston A B. Buy-price English auction [J]. Journal of Economic Theory, 2006, 129(1): 31-56.

[6] Sun D, Li E, Hayya J C. The optimal format to sell a product through the internet: Posted price, auction, and buy-price auction [J]. International Journal of Production Economics, 2010, 127(1): 147-157.

[7] Reynolds S, Wooders J. Auctionswith a buy price [J]. Economic Theory, 2009, 38(1): 9-39.

[8] Gallien J, Gupta S. Temporary and permanent buyout prices in online auctions [J]. Management Science, 2007, 53(5): 814-833.

[9] Simon H A. Models ofbounded rationality: Empirically grounded economic reason [M]. Cambridge, MA: MIT Press, 1997.

[10] Rubinstein A. Modelingbounded rationality [M]. Cambridge,MA:MIT Press, 1998.

[11] Monderer D, Tennenholtz M. Optimal auctions revisited [J]. Artificial Intelligence, 2000, 120(1): 29-42.

[12] Budish E B, Takeyama L N. Buy prices in online auctions: Irrationality on the internet? [J]. Economic Letters, 2001, 72(3): 325-333.

[13] 杜黎, 华桂芬. 固定价格与英式拍卖同时使用时顾客行为分析[J]. 中国管理科学, 2010, 18(5): 113-121.

[14] 田剑, 高杰. 不同一口价网上组合拍卖规则下拍卖方收益分析[J]. 系统管理学报, 2012, 21(2): 246-251.

[15] Jiang Zhongzhong, Fang S C, Fan Zhiping, et al. Selecting optimal selling format of a product in B2C onlineauction with bounded rational customers [J]. European Journal of Operational Research, 2013, 226(1): 139-153.

[16] 杜黎, 刘丽丽, 贾俊秀. 向下降价秒杀中顾客秒杀策略以及卖方期望收益分析[J]. 中国管理科学, 2014, 22(9): 18-25.

[17] 刘树人, 唐沛, 黄颖娜. 网上拍卖销售与逆向拍卖采购下的库存管理[J]. 中国管理科学, 2015, 23(11): 62-69.

[18] Milgrom P R. Auction theory [M]. New York: Cambridge University Press, 1987.

[19] Roth A E, Ockenfels A. Last minute bidding and the rules for ending second price auctions: Evidence from ebay and amazon auctions on the internet [J]. American economic review, 2002, 92(4): 1093-1103.

[20] Tversky A, Kahneman D. Rational choice and the framing of decisions [J]. The Journal of Business, 1986, 59(4): 251-278.

[21] Alba J W, Hutchinson J W. Dimensions of consumer expertise [J]. Journal of Consumer Research, 1987, 13(4): 113-123.

[22] Bettman J R, Luce M F, Payne J W. Constructive consumer choice processes [J]. Journal of Consumer Research, 1998, 25(3): 187-217.

[23] Shen Z J M, Su Xuanming. Customer behavior modeling in revenue management and auctions: A review and new research opportunities [J]. Production and Operations Management, 2007, 16(6): 713-728.

[24] Su Xuanming. Bounded rationality in newsvendor models [J]. Manufacturing & Service Operations Management, 2008, 10(4): 566-589.

Seller’s Revenue in Online Temporary Buyout-price Auctions Considering Bidders’ Bounded Rationality Behavior

GAO Guang-xin1, FAN Zhi-ping2

(1. College of Economics and Management, Nanjing University of Aeronautics and Astronautics, Nanjing 211106, China;2.School of Business Administration, Northeastern University, Shenyang 110167, China)

With the rapid development of information technology, the online auction has broken the limitation of time and space for traditional auction, and greatly expanded the time and space of auction. Then, more customers would like to sell their goods to obtain revenue through the online auction sites such as "eBay.com". With the innovation of online auction format, the online buyout-price auction, including fixed buyout-price, temporary and permanent buyout-price, has been widely applied in online auction business. In practice, the temporary buyout-price auction is a common format of the online buyout-price auction. From the seller point of view, it is important for him/her to estimate the revenue when using the temporary buyout-price auction to sell goods. At present, in most research of online auction, bidders are assumed to be perfect rationality, but previous research has shown that, in a complex and uncertain environment, bidders usually exhibit bounded rationality behavior and such behavior will have impacts on the seller’s revenue. Thus, it is a noteworthy research topic how to conduct the seller’s revenue analysis and set the buyout price in the temporary buyout-price auction with consideration of the situation that bidders are bounded rationality. In this paper, we assume that the bidders are bounded rationality. For the baseline study, we first analyze the bidder’s optimal strategy in the temporary buyout-price auction under the assumption of perfect rationality, and construct the seller’s expected revenue model. Then, the bidding probability-based function for bidders’ behavior choice is adopted to characterize the bidders’ behavior with bounded rationality. On such base, a seller’s expected revenue model is constructed by incorporating the concept of bidder’s bounded rationality behavior into the model for consideration. Furthermore, according to the model, the numerical experiments are conducted to investigate the impacts of three factors (buyout price, number of bidders and degree of bounded rationality) on the seller’s revenue, and the seller’s expected revenue under the assumption of bounded rationality and perfect rationality are analyzed and compared. By the analysis of seller’s revenue and the results of the numerical experiments, some important conclusions are obtained, as well as some managerial insights. Moreover, an example is used to illustrate the feasibility and its potential application of the seller’s expected revenue model. Through the theoretical analysis, we find that the seller’s expected revenue is related to not only the buyout price but also the bidder’s bounded rationality behavior, which bridges the gap between the seller’s revenue and the bidder’s psychological behavior. The seller’s revenue with consideration of bidder’s bounded rationality behavior is almost more than the one based on the assumption of bidder’s perfect rationality. In addition, when the buyout price is low and the number of bidders is large, the seller will obtain more revenue from the temporary buyout-price auction. To effectively estimate seller’s revenue from the temporary buyout-price auction, it is necessary to take into account some crucial influence, such as buyout price, number of bidders, degree of bounded rationality, operational cost and auction participation cost. The seller’s expected revenue model proposed by this paper provides guidance for analyzing and estimating the seller’s revenue in the real online temporary buyout-price auction considering the bidder’s bounded rationality behavior. This paper enriches the theory of online auction and can be studied and applied more widely.

online temporary buyout-price auction; bounded rationality; bidding strategy; expected revenue

2015-06-06；

2017-02-26

国家自然科学基金资助项目(71571039)

樊治平(1961-)，男(汉族)，江苏镇江人，东北大学工商管理学院教授，博士生导师，研究方向：运作管理与决策分析等,E-mail：zpfan@mail.neu.edu.cn.

1003-207(2017)07-0102-11

10.16381/j.cnki.issn1003-207x.2017.07.012

F 724.59

A