基于Petri网的导弹海上补给指挥流程优化分析
刘江胥艳
(1.海军航空工程学院烟台264001)(2.91208部队青岛266000)
基于Petri网的导弹海上补给指挥流程优化分析
刘江1胥艳2
(1.海军航空工程学院烟台264001)(2.91208部队青岛266000)
将Petri网原理应用于导弹海上补给指挥流程的建模与优化,旨在获得最优的导弹海上补给指挥流程。首先阐述了Petri网基本原理,然后建立导弹海上补给指挥流程的Petri网模型,并对导弹海上补给指挥流程的Petri网模型进行优化,结果表明Petri网理论能够明显优化导弹海上补给指挥流程,提高导弹海上补给指挥效率。
Petri网;导弹;海上补给;指挥流程;优化
Class NumberTJ762.3
1 引言
导弹海上补给指挥流程从时间层面上,可分为:导弹海上补给准备阶段指挥流程、导弹海上补给实施阶段指挥流程和导弹海上补给撤收阶段指挥流程[1]。导弹海上补给指挥流程优化,主要是对导弹海上补给准备阶段的各执行环节进行建模分析[2]。目前,应用于流程优化的分析方法比较多,较为常用的是基于随机过程的Petri网分析方法,其分析指标一般分为三类:一类是系统的各种吞吐率;第二类是系统的各种响应时间,即从系统得到任务输入到输出任务结果之间的时间;第三类是各种资源的利用率,即在给定时间区间内,各种系统部件被使用的时间与整个时间之比[3]。根据战时导弹海上补给指挥对时间的快速要求,本文采用第二类指标中的平均延时时间进行分析。
导弹海上补给指挥流程优化分析的基本思路:建立导弹海上补给准备阶段指挥流程的Petri网模型,将指挥流程中的各个执行环节一一映射到Petri网上,指挥流程中的“起点”和“终点”用库所表示条件,执行环节用变迁表示,整个流程网模型由串行、选择、并行、循环这四种路由结构按照一定的方式组合成可以顺利执行的工作流关系,并通过简单的图形清晰地直观出来,最后通过计算比较优化前后Petri网流程模型的平均等价延时时间,验证模型的合理性和优化结论的正确性[4~5]。
2 Petri网流程优化方法
2.1 Petri网建模原理
Petri网是Carl Adam Petri于1962年在博士论文《用自动机通信》中首次提出来的一种自动机网状结构模型,拥有能恰当处理因果上的不存在依赖性的并行现象和表示不确定性的选择的能力,以及以系统模型用网状图形表示的方法[6]。传统的Petri网是简单的过程模型,由库所(place)和变迁(transition)这两类节点以及有向弧等元素组成。库所表示系统的状态,用圆圈表示条件,一方面确保行动按正确的顺序执行,另一方面用来表示任务的状态。变迁表示资源的消耗、使用及使系统状态产生的变化,用矩形表示。变迁的发生受到系统状态的控制,即变迁发生的前置条件必须满足,变迁发生后,某些前置条件不再满足,而某些后置条件则得到满足。此外,库所中包含的黑点称为“托肯”,用来表示工作流执行的状态。只有每个输入库所至少有一个托肯,变迁才能够实施。
定义:Petri网用一个三元组表示的N=(P,T;F)[7],其中P={} p1,p2,···,pm是一个有限的库所集合;T={} t1,t2,···,tn是一个有限的变迁集合;F=(P×T)∪(T×P)是输入函数和输出函数集,称为流关系集合,并满足以下条件:
1)P∩T=φ,规定了库所和变迁是两类不同的元素。
2)P∪T≠φ,表示库所和变迁中至少有一个元素。
3)F=(P×T)∪(T×P),建立了从库所到变迁、从变迁到库所的单方向联系,并且规定同类元素之间不能直接联系。
库所集合和变迁集合的并集称为Petri网的元素集。库所集合和变迁集合是Petri网的基本成分,流关系F是由它们构造出来的,所以在F前面用分号隔开。每个库所代表一种资源,库所中的“托肯”表示可用的资源,资源的流动由流关系规定,所以变迁只能与库所有直接的流关系。不参与任何变迁的资源表现为孤立的库所;不引起资源流动的变迁表现为孤立的变迁[8~10]。
2.2 Petri网四种基本模型及其性能等价公式
1)串行模型及其性能等价公式
串行模型用来描述执行某项任务时,任务中的前后行动按部就班地实施的过程。例如,在导弹海上补给准备过程中,补给指挥员理解任务、判断情况、定下决心、下发指示、组织协同这些活动是按固定顺序完成的,因此就可以用串行模型来表示,如图1所示。
串行模型性能等价公式:设有n个串行变迁组成一个系统A,这n个串行变迁的延时时间为n个相互独立的随机变量,且分别服从参数为λ1,λ2,···,λn的指数分布函数,即n个变迁的平均的总的等价延时时间为
2)选择模型及其性能等价公式
选择模型用来描述执行某项任务时,任务中的各分步行动间相互排斥,需要在两个或多个行动中选择其中一个来执行的过程。例如,补给舰在对接收舰实施导弹海上补给完毕后,补给指挥员要根据战场态势决策是空载的补给舰返回港口补充,然后再返回补给海域待命;还是由接力补给舰从港口驶出,向已经空载的补给舰补充导弹;或是满载导弹的补给舰驶向补给海域,空载的补给舰返回港口。因此,导弹海上补给方案优选就是一个典型的选择模型,如图2所示。
选择模型性能等价公式:设有n个选择变迁组成一个系统B,这n个选择变迁的延时时间为n个相互独立的随机变量,且分别服从参数为λ1,λ2,···,λn的指数分布函数,并设执行变迁的概延时时间为
3)并行模型及其性能等价公式
并行模型用来描述执行某项任务时,任务中的多步行动同时展开或以任意次序分头展开的过程。例如,在海上编队指挥所制定海上兵力行动计划时,各种计划是分头同时制定的,而后再进行汇总,可以用并行模型来表示,海上兵力行动计划汇总并行模型如图3所示。
并行模型性能等价公式:设有n个并行变迁组成一个系统C,这n个并行变迁的延时时间为n个相互独立的随机变量,且分别服从参数为λ1,λ2,···,λn的指数分布函数,则这n个并行变迁的总的等价延时时间:
4)循环模型及其性能等价公式
循环模型用来描述执行某项任务时,任务中一些行动需要重复执行,直到达到预期效果之后才能执行下一步行动的过程。例如,在导弹海上补给实施过程中,补给指挥员要时刻关注战场局势的变化,下达控制指令,判断是否完成了预定的补给任务,而导弹海上补给指挥员决策的过程就可以用循环模型来表示,如图4所示。
循环模型性能等价公式:设两个选择执行变迁T1,T2的延时时间为两个相互独立的随机变量,且分别服从参数为λ1,λ2的指数分布函数,并假设执行完变迁T1后,返回循环执行变迁的概率为α,则这两个循环变迁的总的等价延时时间为[11]
3 导弹海上补给指挥流程优化
3.1 导弹海上补给指挥现行基本流程
导弹海上补给准备阶段是导弹海上补给能否顺利实施的基础和关键。这一阶段指挥流程一般可简单描述为以下六个主要部分:
1)领受并传达导弹海上补给任务。补给指挥员领受导弹海上补给任务后,应将上级对导弹海上补给工作的指示及时向参与海上补给工作的有关人员传达,明确实施导弹海上补给行动需要完成的各项准备工作的时限。
2)开设海上补给指挥所。补给指挥员应根据导弹海上补给指挥的实际需要,适时开设海上补给指挥所,明确海上补给指挥所的具体编成、开设地点和时间,细化各指挥部位和保障分队的责任分工。
3)定下导弹海上补给决心。补给指挥员经过分析研判导弹海上补给任务,结合指挥所各部位的保障建议,初步定下导弹海上补给决心,其内容主要包括:海上补给兵力的编成、配置、任务区分;补给各阶段装备抢救、修理的方法措施;补给通信联络、防卫的组织等。
4)提出导弹海上补给情况报告建议。补给指挥员定下决心后要根据其决心,迅速按照海上编队指挥所规定的时间、方式和要求向其提出报告建议。内容可就海上编队指挥所必须了解,并需其作出决定的几个主要问题提出报告和建议。
5)拟制导弹海上补给实施计划。补给指挥员应及时组织拟制海上补给实施计划。计划内容主要围绕海上补给兵力的区分、编组;实施导弹海上补给的路线、顺序和方法;通信联络的规定;防卫的规定;协同的有关事项等。计划通过则以海上补给指示的形式下发给海上补给兵力各保障分队,若未通过则返回进行修改,等待下一次的审批。
6)下发导弹海上补给指示。在海上补给实施计划审批通过后,以导弹海上补给指示的形式下发给海上补给兵力各保障分队。
3.2 导弹海上补给指挥Petri网模型
在分析描述导弹海上补给指挥流程的基础上,提取流程中的主要环节,完成指挥流程到Petri网模型的映射,确定模型中的主要元素(库所、变迁、托肯)类型以及元素属性项结构模型,列表反映所有的状态和事件,并确定其对应到库所和变迁的标示,明确状态和事件之间输入输出的关系[12]。建立的导弹海上补给指挥流程Petri网模型如图6所示,模型中库所和变迁的含义如表1所示。
指挥流程Petri网模型中各指挥环节的平均时间假设如表2所示。

表1 导弹海上补给指挥流程Petri网模型中库所和变迁的含义
设图6中的所有变迁延时时间为相互独立的随机变量,且分别服从参数为λi,i=1,2,3,···,12的指数分布,即12个变迁的平均表2中的各指挥环节平均时间计算得到。由于变迁T1,T2,T3,T4,T5,T6,T7,T8满足串行模型结构,记为T1-8;变迁T9,T11满足循环模型结构,记为T9,11,执行循环概率为α;变迁T10,T12也满足串行模型结构,记为T10,12。因此,整个导弹海上补给指挥流程Petri网模型可以看作是由2个串行模型和1个循环模型组合而成,只需分别计算出3个变迁的平均延时时间,再求和即可得到流程总的平均延时时间。
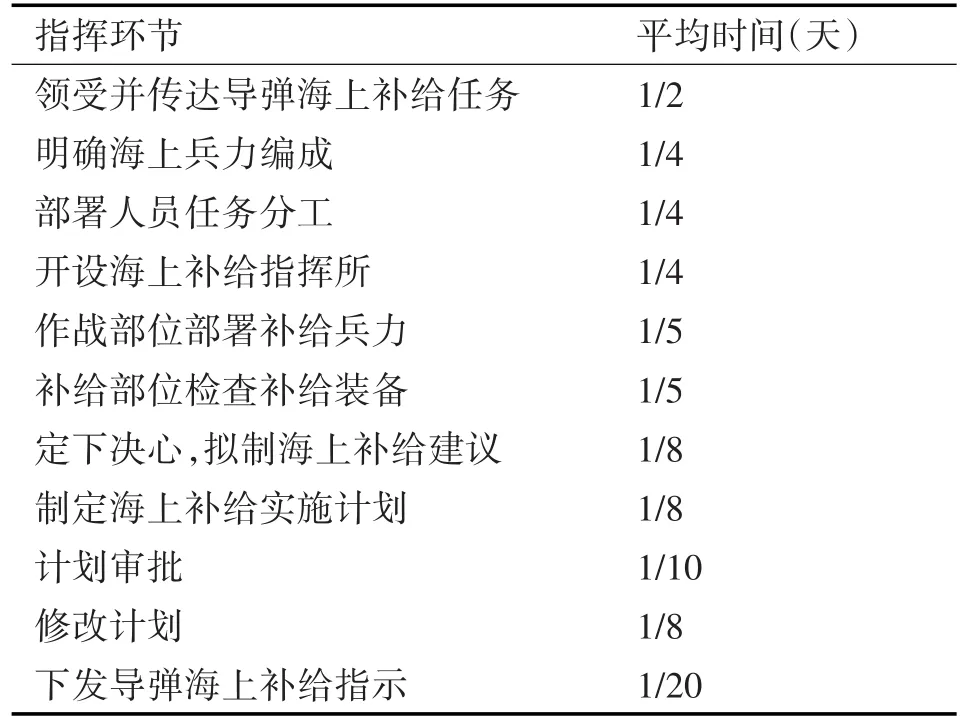
表2 指挥流程Petri网模型中指挥环节及平均时间
根据流程中各指挥环节的平均时间计算λi的值,λ1=2,λ2=4,λ3=4,λ4=4,λ5=5,λ6=5,λ7=8,λ8=8,λ9=10,λ10=10,λ11=8,λ12=20,并设α=0.6。
由式(1)计算串行模型的平均延时时间:由式(4)计算循环模型的平均延时时间:
则流程总的平均等价延时时间:
4 改进模型优化分析
由建立的导弹海上补给指挥流程Petri网模型可知,串行结构是指挥流程中出现频率最高的结构,这种结构的优点是指挥关系清晰,层次清楚,但指挥效率不高。信息化战场的环境要求海上补给指挥高效迅速,由此必须改进指挥流程。可以考虑将流程中的串行结构改为并行结构,提高整个导弹海上补给指挥流程的平均完成时间、资源利用效率等,从而能够提高指挥效率。
分析指挥过程可知,在领受导弹海上补给任务后,明确海上兵力编成T2和部署人员任务分工T3这两个指挥环节可以通过召开补给任务部署会,由补给指挥员与各部负责人以及保障分队主官在会议中同时完成,因此,认为这两项工作可以同时展开,在指挥过程模型中可以将其改为并行模型。此外,在海上指挥所开设完毕后,各指挥部位开始履行职责,其中作战部位部署海上兵力T5和补给部位检查补给装备T6这两项工作基本上少有交叉,不必采用串行模型,也可以采用并行模型。由此,可以改进现行的指挥流程图如图7所示,其对应的新的Petri网模型如图8所示。
根据并行模型的化简方法,变迁T2,T3等价于一个变迁T2,3;T5,T6等价于一个变迁T5,6;变迁T9,T11仍然满足循环模型结构,记为T9,11,执行循环概率为α;变迁T10,T12也满足串行模型结构,记为T10,12。因此,整个导弹海上补给准备阶段指挥流程Petri网模型可以看作是由2个串行模型和1个循环模型组合而成,只需分别计算出3个变迁的平均延时时间,再求和即可得到流程总的平均延时时间。
由式(2)计算并行模型的平均延时时间:
则流程总的平均等价延时时间:
通过对比可以发现,采用改进的并行模型,指挥过程的平均延时时间从2.4875下降为2.2625,说明在导弹海上补给准备阶段,将指挥流程中不存在严格的先后顺序的指挥环节合理并行,可有效降低流程平均等价延时时间,提高导弹海上补给的指挥效率。
5 结语
针对如何提高导弹海上补给指挥效率的问题,运用Petri网建模分析方法,对导弹海上补给指挥流程进行优化分析。通过将导弹海上补给指挥流程中不存在因果依赖关系的串行指挥环节改进为并行执行,达到了优化导弹海上补给指挥流程的目的,进一步提高了导弹海上补给指挥效率。分析结果表明Petri网建模分析方法非常适合解决导弹海上补给指挥流程的优化问题,值得进一步推广应用。
[1]张耀鸿,樊建才,廖晓林.基于Petri网的指挥控制流程仿真方法[J].系统仿真学报,2012,24(7):1418-1421.
[2]关成彬,段立.Petri网在海军战役装备保障指挥中的应用[J].兵工自动化,2008,27(12):6-7.
[3]林闯.随机Petri网和系统性能分析[M].北京:清华大学出版社,2003:53-57.
[4]洪国彬.基于随机Petri网的企业业务流程重组和优化的理论方法研究[D].天津:天津大学,2003:35-41.
[5]罗雪山,罗爱民,张耀鸿.Petri网在C4ISR系统建模、仿真与分析中的应用[M].长沙:国防科技大学大学出版社,2007:116-122.
[6]袁崇义.Petri网原理与应用[M].北京:电子工业出版社,2005:77-82.
[7]朱敏洁,谭亚新,马亚龙.作战指挥工作流程建模方法[J].装备甲兵工程学院学报,2006,20(6):17-20.
[8]翟建设,王勇,吴青.基于人员-时间Petri网的气象业务保障流程模型[J].计算机应用与软件,2008,25(1):49-51.
[9]陈奇伟.基于广义随机Petri网的导弹新型打击流程建模与分析[J].中国电子科学研究院学报,2006,12(6):496-501.
[10]张瑾.协同设计中工作流管理研究[D].重庆:西南交通大学,2005:41-45.
[11]孙宝琛,王亚彬,郭勇.基于Petri网的装备维修保障指挥过程建模与性能优化分析[J].指挥控制与仿真,2011,33(1):113-117.
[12]张玉洁.基于Petri网的铁路集装箱运输流程建模与优化研究[D].北京:北京交通大学,2007:53-57.
Optimized Analysis for the Command Process of Missile Replenishment at Sea Based on Petri Net
LIU Jiang1XU Yan2
(1.Naval Aeronautical and Astronautical University,Yantai264001)(2.No.91208 Troops of PLA,Qingdao266000)
This paper applies the Petri Net to model and optimizes the command process of missile replenishment at sea expected to have the best excellent command process of missile replenish at sea.Firstly,it expounds the Petri Net basic theory,and then establishes the basic model about the command process of missile replenish at sea,finally utilizes the Petri Net modeling and optimizing the command process of missile replenish at sea.The results show that the Petri Net theory is able to significantly optimize the command process of missile replenish at sea and improve the efficiency of the missile replenish at sea.
Petri Net,missile,replenishment at sea,command process,optimizing
TJ762.3
10.3969/j.issn.1672-9730.2017.07.008
2017年1月1日,
2017年2月19日
刘江,男,硕士研究生,研究方向:海军航空、导弹装备综合保障。胥艳,女,研究方向:信息与通信工程。

