基于响应面方法的微型车车门模态分析与优化
秦训鹏 冯佳伟 王永亮 金磊
1.武汉理工大学汽车工程学院,武汉,4300702.现代汽车零部件技术湖北省重点实验室,武汉,430070
基于响应面方法的微型车车门模态分析与优化
秦训鹏1,2冯佳伟1,2王永亮1,2金磊1,2
1.武汉理工大学汽车工程学院,武汉,4300702.现代汽车零部件技术湖北省重点实验室,武汉,430070
应用灵敏度分析方法和响应面法,优化车门结构模态。建立车门的有限元数值仿真模型,并通过约束模态测试对仿真模型进行标定。对车门第三阶模态频率关于车门板件厚度的灵敏度进行了研究,筛选出高敏板件并以这些板件的厚度为设计变量,运用面心复合设计方法获取样本点,构建了车门第三阶模态频率的二阶显式响应面函数。基于此响应面函数进一步建立了优化模型,结果显示改进车门厚度后,车门和白车身模态分离,同时实现省材5.83%。
灵敏度分析;响应面;模态;优化
0 引言
车门作为车身的一个重要组成部分,其模态频率分布对车身的动态性能有较大的影响,当车门和白车身的模态频率匹配不合理时,结构间模态耦合会较强,使车身结构振动增大,因此,对车门结构设计而言,匹配车门和白车身的模态频率十分重要。朱茂桃等[1]利用Kriging算法构建近似模型对车门进行分析,在满足扭转刚度和模态性能要求的同时,实现车门的轻量化。胡朝辉等[2]采用均匀拉丁方实验设计方法获取样本数据,并采用响应面方法构建了多学科系统的近似模型,使车门系统的下垂刚度、强度及侧碰性能提高的同时,减小了车门系统质量。曹文钢等[3]、叶盛等[4]通过灵敏度分析筛选高敏设计变量,并证明了基于灵敏度分析优化的可行性。杨搏等[5]建立了某SUV车身和乘客室声腔的有限元模型,通过结构声学灵敏度分析识别出主要的噪声源,针对主要声源提出改进措施,有效降低了车内噪声。昌辉成等[6]、方柘林等[7]以车门垂直刚度和结构的一阶模态为目标,实现了多目标优化。PARK[8]对线性动态响应方法的研究表明,近似模型能够较好代替有限元模型进行优化设计。然而,联合运用灵敏度方法和响应面方法,构建模态频率的响应面分析模型来开展车门与白车身模态匹配的研究较少,鉴于此,本文构建车门模态频率的响应面优化模型,优化车门和白车身的模态匹配,在改善车门模态性能的同时,实现车门的轻量化。
1 数值仿真模型建立与标定
1.1 车门有限元
车门有限元模型前处理在HYPERWORKS软件内实现,求解计算在MSC.NASTRAN软件中进行。车门主要由薄壁件(包括内外板、支撑板、内饰板和玻璃等)组成,对这些薄壁件用板壳单元建模,为了避免因三角形单元较多导致模型整体刚度过大,使仿真模型不准确的问题,建模过程中严格控制三角形单元的数量(不超过3%)[9]。车门的材料为普通钢(弹性模量Es=210 GPa,密度ρs=7.8×103kg/m3,泊松比μs=0.3,阻尼忽略),车窗玻璃为普通玻璃,材料的简化参数为弹性模量Eg=69 GPa,密度ρg=2.5×103kg/m3,泊松比μg=0.3,不考虑阻尼。车门部件间的连接为点焊和粘接,粘接用ACM2单元模拟,黏接材料为黏性胶(弹性模量EG=50 MPa,密度ρG=1.2×103kg/m3,泊松比μG=0.49,阻尼系数0.1)。对于板壳单元,网格平均尺寸为8 mm,最终车门有限元模型的单元数为65 388,其中,三角形单元数为1856(占比为2.84%)。运用模态叠加法求解车门结构的约束模态;在有限元模型中,释放车门铰链处绕Z轴的转动,约束门锁安装孔处Y方向的平动,有限元模型的坐标系与车辆整车坐标系一致。为了减小计算过程中的截断误差,模态叠加法计算时的截止频率至少为所关注频率的2倍。
1.2 车门数值模型标定
为说明所建立的数值仿真模型的精度,开展车门约束模态测试。对于车门这种结构,通过多点激励单点测量的方法,共获取54个点的振动数据。数值仿真和模态测试的结果如表1所示,由表1可知,仿真模态和实验模态振型吻合,相对误差在可接受范围,这表明数值仿真模型可以很好地模拟实际车门结构的动态性能,数值仿真模型的精度较高。

表1 数值仿真和测试的模态结果Tab.1 Modal results of numerical simulation and test
车门的第三阶模态振型如图1所示,模态振型主要为车门内板的局部振动,振动较大的位置为车内内板、车门外板下部和车门下支撑板。车门通过旋转铰链和关门锁固定在白车身上,白车身的第九阶模态(第二阶扭转模态)频率为42.4 Hz(图2),和车门第三阶模态频率很接近,容易产生结构共振;而车门其他阶模态的频率分布与白车身的模态频率分布均有1.2 Hz以上的间隔,实现了模态分离,即此车门第三阶模态和白车身模态匹配不好,需改进。

图1 车门第三阶结构模态Fig.1 The third order structure mode of the door

图2 白车身第九阶结构模态Fig.2 The ninth order structure mode of the white body
2 模态频率关于板厚灵敏度分析
对于车门这种由大量薄壁结构连接而成的结构,可以通过优化板件的厚度匹配来改进车门结构的模态分布。在优化车门板件厚度之前,首先对车门模态频率相对于车门板件厚度的灵敏度进行研究[10-11]。通过灵敏度计算结构响应对各设计变量的敏感程度,反映结构设计变量对结构性能的影响,找到主要敏感部位,这种方法在获取设计变量方面更有针对性,极大地提高优化效率。
车门模态频率相对于车门板件厚度的灵敏度为
(1)
其中,f(X)=f(x1,x2,…,xn) 为车门的结构模态频率,是板厚变量X=(x1,x2,…,xn)的函数,xi为第i个板件的厚度。则第j阶模态频率关于第i个板件的厚度的灵敏度为
(2)
在工程上习惯用差分来近似计算偏微分,则第j阶模态频率关于第i个板件的厚度的灵敏度的中心差分表达式为
Δxi,…,xn)-fj(x1,x2,…,xi-Δxi,…,xn))
(3)
基于上述理论方法,开展车门第三阶模态频率关于板件厚度的灵敏度研究,以内板厚度t1、外板加强板厚度t2、内板下加强板厚度t3、窗框加强板厚度t4、竖直加强板厚度t5和中部加强板厚度t6为初选变量。为了减小各板件质量差异对灵敏度的影响[12],用式(3)求解的灵敏度均除以各板件的原始质量(单位质量下频率关于板厚的灵敏度值),式(3)中的Δxi=0.05xi。运用式(3)和车门有限元模型,计算的第三阶模态频率关于板件厚度的灵敏度结果如表2所示。由表2可知,车门第三阶模态频率关于内板、外板加强板、内板下加强板和窗框加强板板厚的灵敏度结果幅值较大,分别为61.43 Hz/mm、2.86 Hz/mm、4.62 Hz/mm和-124.0 Hz/mm,这些板件在单位质量下频率关于板厚的灵敏度值仍较大,分别为3.17 Hz/(mm·kg)、0.51 Hz/(mm·kg)、1.05 Hz/(mm·kg)和-25.3 Hz/(mm·kg),这表明单位质量下变动这些板件的厚度会使第三阶模态频率的值变化较显著。其中,t1、t2、t3的灵敏度为正数,表示在一定范围内,随着板件厚度增加,车门第三阶模态频率f3逐渐增大,且增大的速度较明显;t4的灵敏度为负数,表示在一定范围内,随着板件厚度减小,车门第三阶模态频率f3逐渐增大,且增大的速度较明显。选择t1、t2、t3与t4为变量(分别记为x1、x2、x3、x4),通过改变板件厚度,在车门质量不显著增加的前提下,可以有效改进车门第三阶模态频率,优化车门模态与白车身模态的匹配。通过第三阶模态频率f3关于板件厚度的灵敏度研究,我们从众多结构板件中挑选出了关键性板件,使待优化的变量更有针对性,并降低了待优化模型的规模。
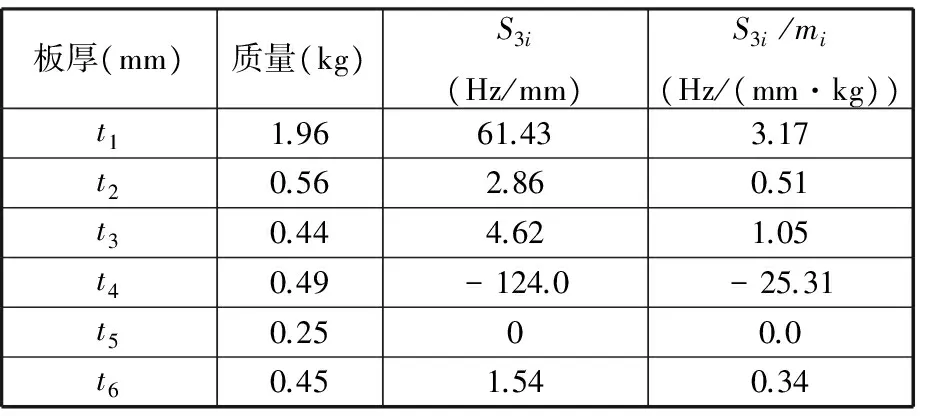
表2 车门第三阶模态频率关于板件厚度的灵敏度Tab.2 Sensitivity of the third order modal frequencies to plate thickness
3 模态频率的响应面模型
响应面方法基于统计学和试验设计技术,获得输入变量(筛选出来的板厚变量x1、x2、x3、x4)和输出变量(车门第三阶模态频率f3)的数学函数关系,在可接受的误差范围内,运用构建的响应面模型代替车门有限元模型开展分析与优化,响应面的构建过程包括设计变量、试验设计、模型构建三部分。响应面方法的理论参见文献[11, 13]。
3.1 设计变量
考虑到各板件的加工工艺要求,板件的厚度范围设计如表3所示。
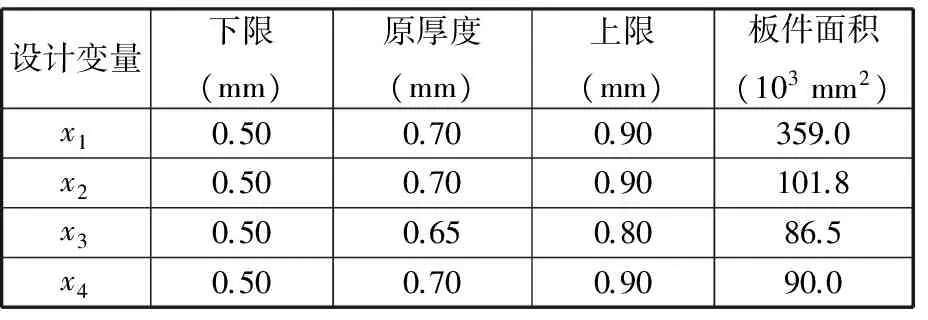
表3 设计变量的取值范围和对应板件的面积Tab.3 Range of design variables and area of corresponding plate
3.2 面心复合设计
通过设计一系列样本试验,在运用尽量少的资源和计算时间前提下,获得能反映设计目标的高度相关信息数据[10]。对试验设计而言,在设计域内选择一组样本点分布很重要,一组差的样本点会影响所建立的响应面模型的精度。相对于中心复合设计,面心复合设计的轴点被设置为±1的水平,使设计变量限定在设计域内;相对于全因子设计,面心复合设计在不显著影响精度的条件下,所需的样本点更少。鉴于以上两个优点,本文采用面心复合设计来获取样本点。四因素三水平的面心复合设计问题需25个样本点,运用有限元方法分别求解这25组样本点对应的车门第三阶模态频率,试验设计的结果如表4所示。

表4 第三阶模态频率关于设计变量的面心复合设计Tab.4 Surface centered composite design of the third order modal frequencies to design variables
注:FEM为在有限元中求解得到的频率,RSM为在响应面中求解得到的频率,ε为相对误差。
3.3 车门模态频率的响应面模型
为了得到设计变量和响应之间的数学关系,构建车门第三阶模态频率关于设计变量的二阶响应面模型,其数学表达式为
(4)
其中,α0、αi、αii、αij是未知系数,可以通过最小二乘法获得。根据表4中的数据可以求解α0、αi、αii、αij,则车门第三阶模态频率的二阶显式响应面函数为
f3=31.81+19.89x1+0.43x2-0.13x3+0.8x4-
(5)
在每个样本点下,运用响应面方程(式(5))计算车门第三阶模态频率(表4中的RSM)。由表4可知,有限元法和响应面法计算所得车门第三阶模态频率的相对误差很小,文中所建立的响应面(式(5))可以较好地拟合样本数据,即在整个设计域内,可用此响应面函数代替有限元模型来优化板件厚度,改进车门模态频率分布。
运用响应面函数(式(5))研究车门第三阶模态频率关于设计变量的关系,结果如图3、图4所示。由图3可知,车门第三阶模态频率关于x1和x4的变化明显,最大值为43.67 Hz(x1=x4=0.9 mm),最小值为40.31 Hz(x1=x4=0.5 mm);图3b中,等高线的梯度方向从侧面给出了优化车门模态频率时变量的收敛方向。由图4可知,车门第三阶模态频率对于x2和x3的变化不敏感,频率变化范围为42.21~42.55 Hz,即只优化变量x2和x3不能将车门频率和白车身频率隔离。对比图3、图4可知,x1和x4的变化对车门第三阶模态频率敏感,此结论和表2中灵敏度分析的结果吻合。
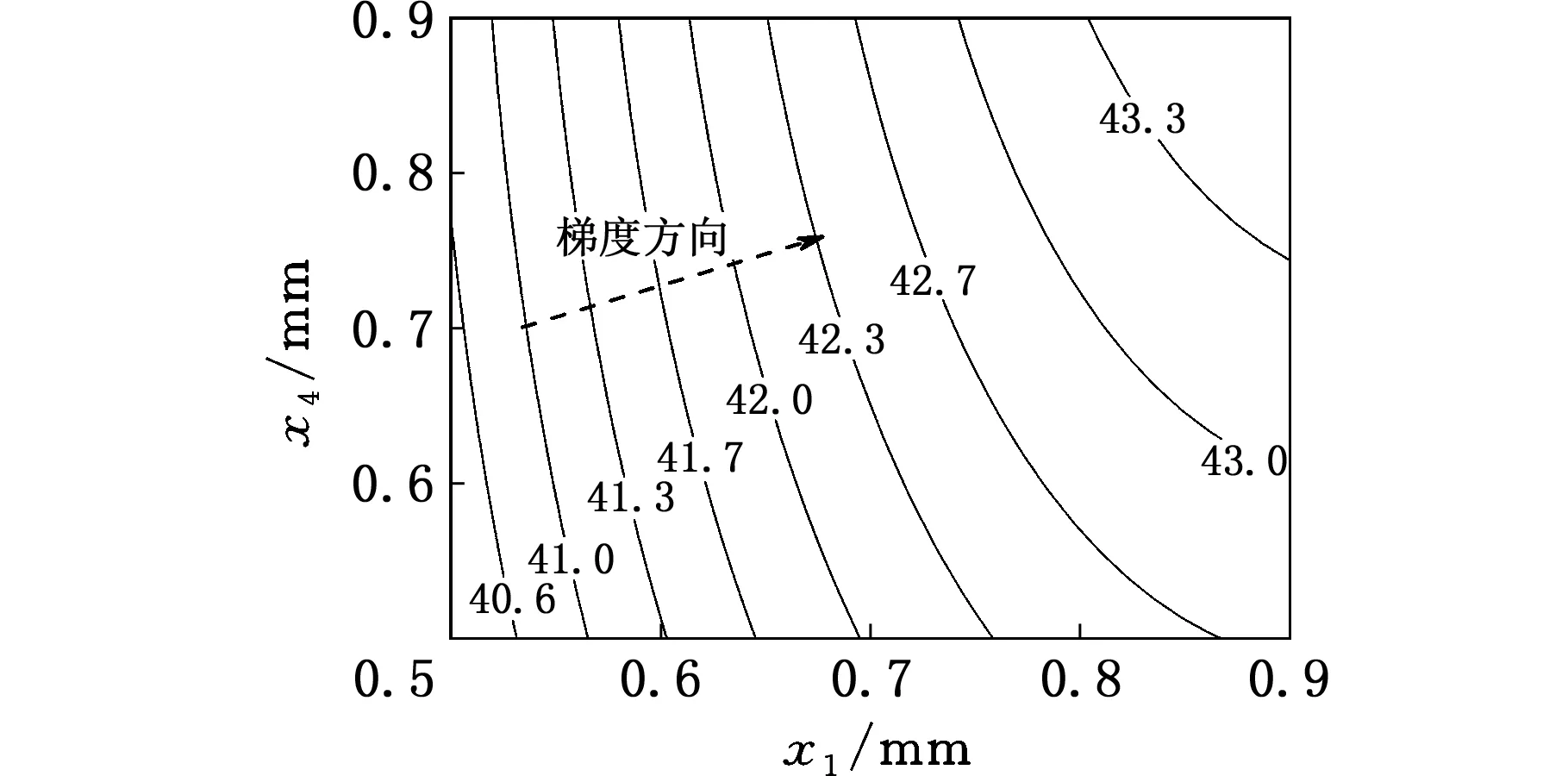
(b)车门第三阶模态频率的等高线图图3 车门第三阶模态频率关于设计变量x1和x4的响应面 (x2 =0.7 mm,x3=0.65 mm)Fig.3 Response frequencies of the third order modal frequencies to x1 and x4(x2=0.7 mm, x3=0.6 5mm)

(a)车门第三阶模态频率的响应面
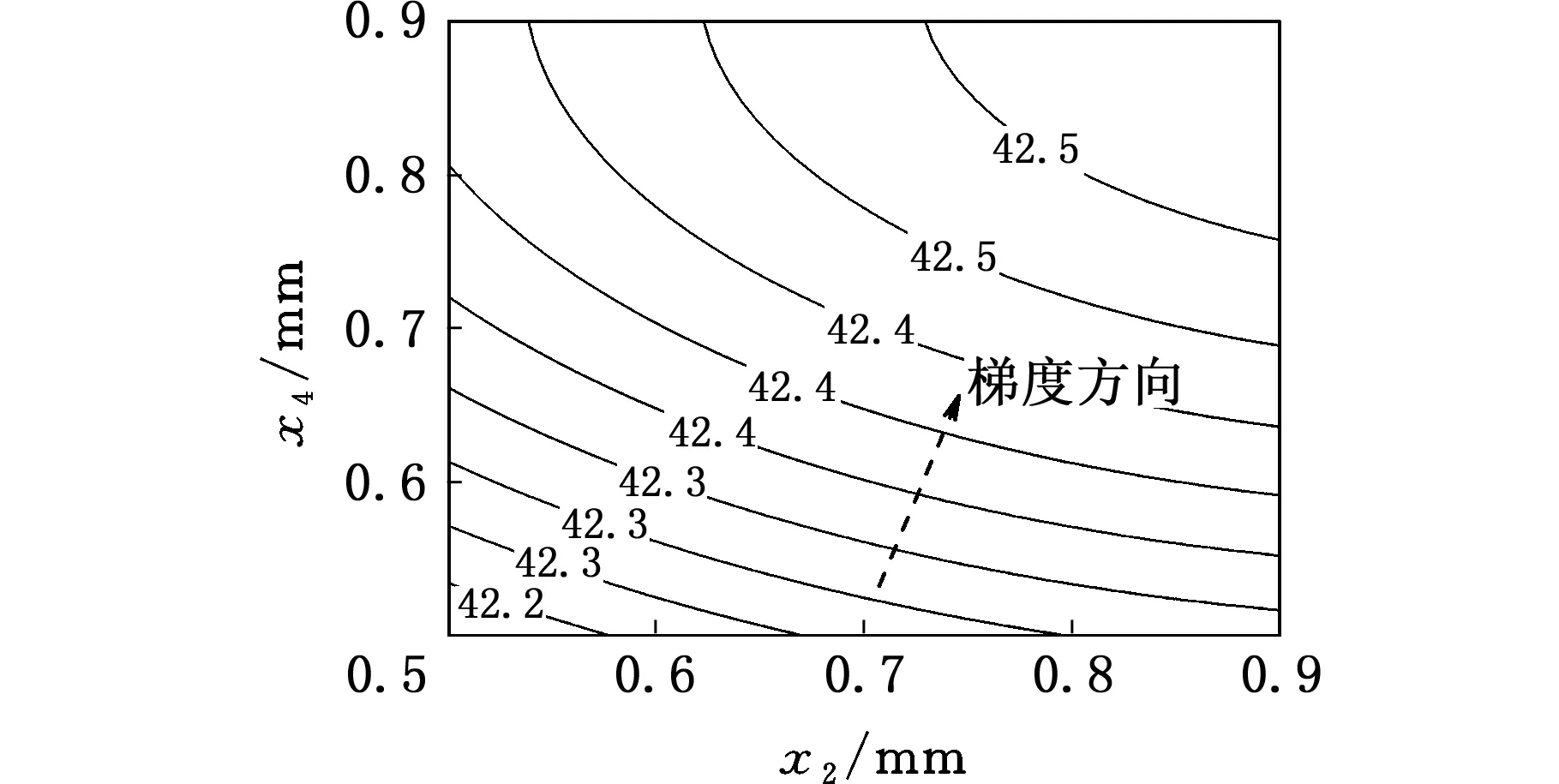
(b)车门第三阶模态频率的等高线图图4 车门第三阶模态频率关于设计变量x2和x3的响应面 (x1 =x4=0.7 mm)Fig.4 Response frequencies of the third order modal frequencies to x2 and x3(x1 =x4=0.7 mm)
4 车门模态频率优化
由于车门第三阶模态频率f3=42.4 Hz,与白车身第九阶模态频率f9=42.4 Hz很接近,导致车门安装在白车身上容易结构共振,为此,需对车门结构进行优化来改进模态频率分布,使车门结构模态的第三阶频率与白车身模态频率错开,而车门其他阶模态的频率保持与白车身模态频率有一定的间隔,且车门整体的Y方向刚度不明显降低,这样可满足车门的侧撞性要求。由于车门第三阶模态频率响应面模型可以高精度地替代有限元模型,来研究模态频率f3关于关键板件厚度的数值关系,故应用第三阶模态频率的响应面函数来构建优化模型。以x1、x2、x3和x4为优化设计变量,约束变量的上下限见表3,以车门总质量不增加为约束条件,以车门第三阶模态频率f3与白车身第九阶模态频率f9相差最大为优化目标,参看表4中的第7列数据和图3b的梯度方向可知,车门第三阶模态频率f3较小时,其与白车身第九阶模态频率f9相距较远,建立的优化模型为
(6)
运用MATLAB工具箱中的遗传算法求解式(6)的优化模型,目标函数经过两次插值迭代后收敛,此时设计变量x1=x2=x3=x4=0.5 mm,目标函数的最小值为40.24 Hz,与白车身第九阶模态频率相差2.17 Hz,实现了车门和白车身模态频率分离。在3.30 GHz 计算机上,运用优化模型(式(6)),计算机的求解时间是14 ms,运用有限元方法计算1次表4中的样本数据对应模型所需的求解时间为53.4 s,优化模型显著的提高了计算效率、节省了计算时间。这是因为运用有限元方法时,大量时间用在控制方程的对角化和解耦,对于节点数较多的有限元模型,这种时间耗费将更显著。分别在车门外板中心加载100 N的力,力的方向沿整车坐标系Y方向,计算优化前后车门的变形,结果如图5所示,初始模型在加载点的刚度为67.1 N/mm,优化后,模型在加载点的刚度为64.6 N/mm,刚度减小3.7%,优化后的车门在薄弱点处Y方向的刚度降低不明显,可满足车门的侧撞性要求。通过响应面方法对板件结构厚度优化后,整个车门质量为15.51 kg,较原车门整备质量的16.47 kg省材5.83% ,通过模态频率匹配优化,不仅改进了结构的动态性能,还节省了材料,实现了轻量化,同时车门的侧碰性能降低不明显。
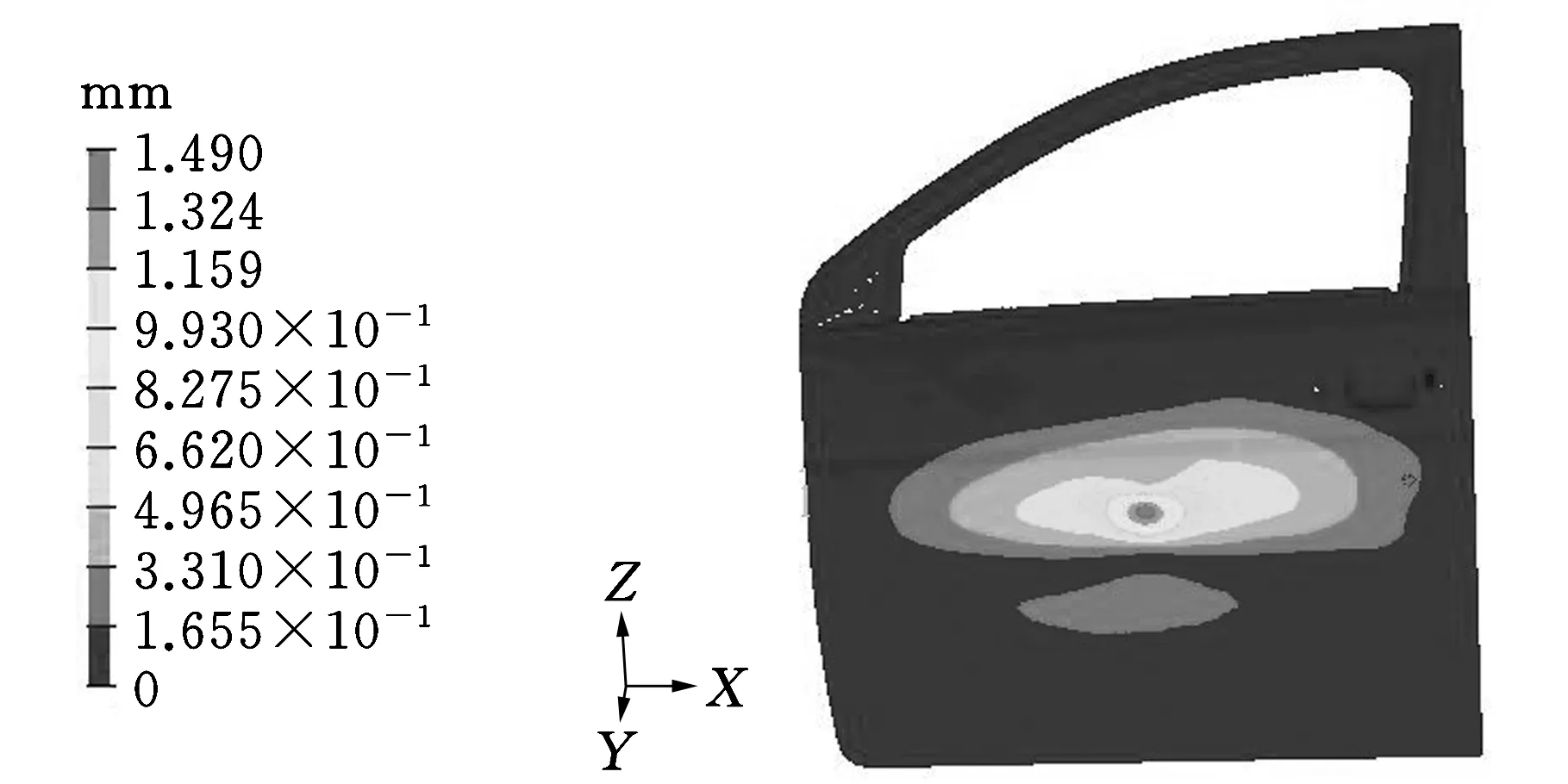
(a)优化前
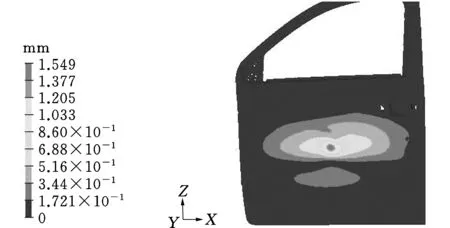
(b)优化后图5 在集中力加载时的车门优化前后的位移分布Fig.5 Displacement distribution before and after optimization of under concentrated load
5 结论
(1)不同的板件,其厚度变化相同时,车门模态频率变化不同,运用中心差分的近似灵敏度计算,获取了车门的高敏面板(内板、外板加强板、内板下加强板与窗框加强板),以筛选出的板厚为设计变量,使车门模态频率优化更有针对性。
(2)运用面心复合设计获取一组样本点,构建了车门第三阶模态频率的响应面函数。此响应面函数拟合精度较高,可以在整个设计域内较好地替代有限元模型进行频率计算,显著提高了计算效率、节省了计算时间。
(3)运用响应面函数构建了车门第三阶模态频率的显式优化模型,对车门模态频率进行了优化,实现了车门和白车身模态频率分离,并实现了车门结构的轻量化,同时车门的侧碰性能降低不明显。
[1] 朱茂桃, 钱洋, 顾娅欣, 等. 基于Kriging模型的车门刚度和模态优化[J]. 汽车工程, 2013,35(11):1047-1050. ZHU Maotao, QIAN Yang, GU Yaxin, et al. Stiffness and Modal Optimization of Car Door Based on Kriging Model[J]. Automotive Engineering, 2013, 35(11): 1047-1050.
[2] 胡朝辉, 成艾国, 王国春, 等. 多学科优化设计在拼焊板车门轻量化中的应用[J]. 中国机械工程, 2010, 20(4):495-499. HU Zhaohui, CHENG Aiguo, WANG Guochun, et al. Application of Multidisciplinary Optimization Design in Lightweight of Tailor Welded Blanks[J]. China Mechanical Engineering, 2010, 20(4):495-499.
[3] 曹文钢, 曲令晋, 白迎春. 基于灵敏度分析的客车车身质量优化研究[J]. 汽车工程, 2009,31(3):278-281. CAO Wengang, QU Lingjin, BAI Yingchun. Bus Body Quality Optimization Based on Sensitivity Analysis[J]. Automotive Engineering, 2009,31(3):278-281.
[4] 叶盛, 辛勇. 基于灵敏度及尺寸优化的汽车车门轻量化[J]. 机械设计与研究, 2013,29(6):112-115. YE Sheng, XIN Yong. Lightweight Design of Car Door Based on Sensitivity and Dimension Optimization[J]. Mechanical Design and Research, 2013,29(6):112-115.
[5] 杨搏, 朱平, 余海东, 等. 基于模态分析法的车身NVH结构灵敏度分析[J]. 中国机械工程, 2008,19(3):361-364. YANG Bo, ZHU Ping, YU Haidong, et al. Sensitivity Analysis of NVH of Body Structure Based on Modal Analysis[J]. China Mechanical Engineering, 2008,19 (3): 361-364.
[6] 易辉成, 杨旭静, 王一骏. 基于多工况的车门结构多目标优化设计方法研究[J]. 微计算机信息, 2012(4):87-89. YI Huicheng, YANG Xujing, WANG Yijun. Study on Multi-objective Optimization Design of Door Structure Based on Multi Conditions[J]. Microcomputer Information, 2012(4):87-89.
[7] 方柘林, 王丽娟, 陈宗渝, 等. 基于车门结构的多目标优化设计方法研究[J]. 机械设计, 2014(8):60-64. FANG Zhelin, WANG Lijuan, CHEN Zongyu, et al. Research on Multi-objective Optimization Design Based on Car Door Structure[J]. Mechanical Design, 2014(8):60-64.
[8] PARK G J. Echnical Overview of the Equivalent Static Loads Method for Non-linear Static Response Structural Optimization[J]. Structural and Multidisciplinary Optimization, 2011, 43(3):319-337.
[9] WANG Y, QIN X, LU L, et al. The Noise Control of Minicar Body in White Based on Acoustic Panel Participation Method[J]. Journal of Vibroengineering, 2016, 18(2):1332-1345.
[10] 邬广铭, 史文库, 刘伟, 等. 基于模态灵敏度分析的客车车身优化[J]. 振动与冲击, 2013, 32(3):41-45. WU Guangming, SHI Wenku, LIU Wei, et al. Optimization of Bus Body Based on Modal Sensitivity Analysis[J]. Vibration and Shock, 2013, 32(3): 41-45.
[11] QIN X, WANG Y, LU C, et al. Structural Acoustics Analysis and Optimization of an Enclosed Box-damped Structure Based on Response Surface Methodology[J]. Materials & Design, 2016,103:236-243.
[12] ZHU P, SHI Y, ZHANG K, et al. Optimum Design of an Automotive Inner Door Panel with a Tailor Welded Blank Structure[J]. Automobile Engineering, 2008, 222(8):1337-1348.
[13] 吕辉, 于德介, 陈宁, 等. 基于可靠性的混合不确定参数汽车盘式制动器振动稳定性分析[J]. 机械工程学报, 2014,50(6):112-119. LYU Hui, YU Dejie, CHEN Ning, et al. Reliability Analysis for Vibration Stability of Automotive Disc Brake System with Hybrid Uncertian Parameters[J]. Journal of Mechanical Engineering, 2014, 50(6): 112-119.
(编辑 张 洋)
Structural Modal Analysis and Optimization of Mini-car Doors Based on Response Surface Method
QIN Xunpeng1,2FENG Jiawei1,2WANG Yongliang1,2JIN Lei1,2
1.School of Automotive Engineering,Wuhan University of Technology,Wuhan,4300702.Hubei Key Laboratory of Advanced Technology for Automotive Conponents,Wuhan,430070
Sensitivity analysis method and response surface method were used to optimize structural modal of the mini-car doors. A finite element numerical simulation model was established, and the simulation model was calibrated by restraint modal tests. In order to screen out high sensitive plates, a sensitivity analysis for the thicknesses of door plates was proposed based on door’s third order modal frequency. Sample points were obtained by face centered composite design while design variables were from the thicknesses of high sensitive plates, and a two order explicit response surface function of vehicle door’s third order modal frequency was established. According to the response surface function, an optimization model was established. The final results show that the modal frequency matching of the door and body in white is optimized after changing the door thicknesses, while materials are saved about 5.83%.
sensitivity analysis; response surface; mode; optimization
2016-09-26
国家自然科学基金资助项目(51605353);教育部创新团队发展计划资助项目(IRT13087);武汉理工大学自主创新研究基金优秀博士培育项目(WUT:2016-YB-025)
U467
10.3969/j.issn.1004-132X.2017.14.009
秦训鹏,男,1962年生。武汉理工大学汽车工程学院教授、博士研究生导师。主要研究方向为汽车生态设计及循环利用、汽车轻量化、汽车零部件3D打印及智能制造、新能源汽车传动系统设计与制造。发表论文70余篇。E-mail:qxp915@qq.com。冯佳伟,女,1993年生。武汉理工大学汽车工程学院硕士研究生。王永亮,男,1988年生。武汉理工大学汽车工程学院博士研究生。金 磊,男,1993年生。武汉理工大学汽车工程学院硕士研究生。

