液压集成块湍流模型修正及内流特性分析

胡建军 陈 进 权凌霄 张 晋 孔祥东

1.燕山大学机械工程学院，秦皇岛，0660042.燕山大学先进制造成形技术及装备国家地方联合工程研究中心，秦皇岛，0660043.燕山大学建筑工程与力学学院，秦皇岛，066004



液压集成块湍流模型修正及内流特性分析

胡建军1,3陈 进3权凌霄1,2张 晋1,2孔祥东1,2

1.燕山大学机械工程学院，秦皇岛，0660042.燕山大学先进制造成形技术及装备国家地方联合工程研究中心，秦皇岛，0660043.燕山大学建筑工程与力学学院，秦皇岛，066004

基于粒子图像测速技术(PIV)建立了带有刀尖角容腔的直角转弯流道流场的数值计算模型，并进行三维流场仿真。通过将数值计算得到的典型涡系结构与实验结果进行对比，考察了工程上常用的7种湍流模型对带有刀尖角容腔直角转弯流场的预测性能。通过定义权重误差K，筛选出S-A模型作为基础湍流模型并对其进行了参数修正。结果表明，当S-A模型Cb1取值从默认值0.1355修正为0.17时，出流方向正对刀尖角容腔模型权重误差值上升25.0%，入流方向正对刀尖角容腔模型权重误差值下降34.7%，修正后的S-A湍流模型对两种直角转弯流场的综合预测精度有所提高。运用筛选修正后的S-A湍流模型分析了4种典型直角转弯流道的内流特性，结果表明圆弧过渡直角转弯流道相比于带有刀尖角容腔的转弯流道具有更小的压力损失。

液压集成块；湍流模型；直角转弯流道；内流特性

0 引言

模块化、可组配、开放式和集成化是液压控制系统的发展趋势[1]。液压集成块作为液压系统集成化安装必不可少的零件已被广泛应用。液压集成块内流道一般采用钻、镗等机械加工手段获得，这导致集成块内带有刀尖角容腔的直角转弯流道大量出现。有研究表明，在流体动力输配过程中，每经过一个液压集成块，其压力损失最高可达1 MPa[1-3]，因此降低集成块压力损失对于液压系统节能具有重要意义，而对直角转弯型流道液流特性进行准确预测是降低流体动力传输过程中能量损失的重要前提。

近年来，计算流体动力学(CFD)及粒子图像测速技术(particle image velocimetry, PIV)得到较快发展，已有一些学者利用上述技术对集成块内部流道的液流特性展开研究。田树军等[2-3]应用CFD技术对液压集成块内部典型流道流场进行了系统的数值模拟研究，从液流特性的角度对液压集成块内部流道进行了优化设计。雷琪等[4]应用CFD技术对液压集成块流道进行研究，分析了不同流速下孔径大小对压力损失的影响。杜经民等[5]利用CFD 方法对实际工况下液压集成块内复杂流道进行建模和仿真，分析了影响液压集成块压力损失的主要因素及液压集成块内部流道结构与液流流动特性的关系。文献[6-7]基于 FLUENT 软件，分析了工艺孔、刀尖容腔对液流压力损失的影响规律，探讨了造成压力损失的原因。苏乃权等[8]仿真分析了液压集成块两种不同孔道的流场以及增大阀口的开度、缩短阀口到集成块交叉孔道的距离后的流场。丁珏等[9]从三维不可压缩雷诺时均Navier-Stokes方程出发,对90°弯曲管道内湍流流动进行数值模拟，研究了来流方向对流场结构和流动特性的影响。

湍流模型的选择对于流动数值模拟至关重要，以上仿真研究所采用的湍流模型各不相同。本文在对直角转弯流道流场进行PIV直接测量的基础上[10]，建立对应的数值计算模型，进行三维流场仿真，分析了工程上常用的7种湍流模型对有刀尖角容腔直角转弯流场的预测能力，筛选出合适的湍流模型并进行了修正。运用修正后的湍流模型对液压集成块中典型直角转弯流道的内流特性进行了仿真模拟，分析了在不同速度工况下典型流道的总压力损失变化规律。

1 有限元模型建立

1.1 几何建模及网格划分

在文献[10]的基础上，选取了两种实验模型的测量结果用以检验和修正湍流模型。实验模型中刀尖角容腔孔长度l=50%d(d为流道直径)，阀块参数定义和实验测量结果如图1所示。由实验结果可知，流体经过直角转弯时，在刀尖角容腔内和出流段产生两处旋涡，分别在图中标注为A涡和B涡，其形成机理详见文献[10]。后文将以A涡和B涡的涡核位置作为检验和修正湍流模型的基准。

(a)入流方向正对刀尖角实验模型

(b)出流方向正对刀尖角实验模型

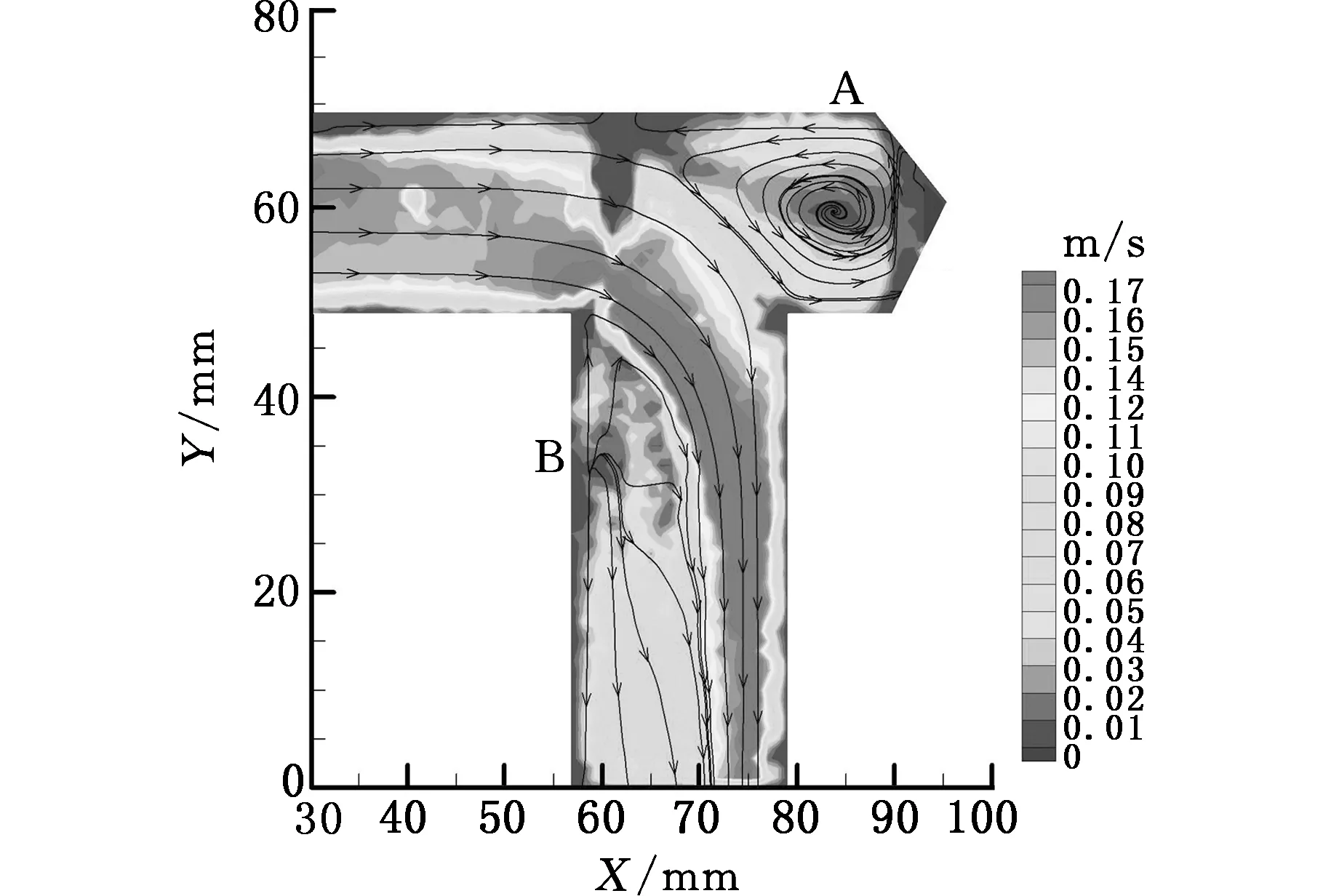
(c)入流方向正对刀尖角PIV测量结果

(d)出流方向正对刀尖角PIV测量结果图1 直角转弯流道实验模型及PIV测量结果Fig.1 Experimental model and PIV results of right angle channel

采用GAMBIT软件对两种直角转弯流道进行建模与网格划分，考虑流道几何结构不规则性，运用非结构四面体网格对计算流域进行网格划分。以进口质量流量为指标考察计算结果对网格的依赖性，结果见图2。通过观察可知，当主体网格数超过50万后，进口质量流量变化趋缓。同时，计算得到量纲一壁面距离Y+介于1～5之间，这与选用的湍流模型和壁面函数是匹配的。考虑到计算精度和计算代价的平衡，后续计算模型的网格数均在50万左右。

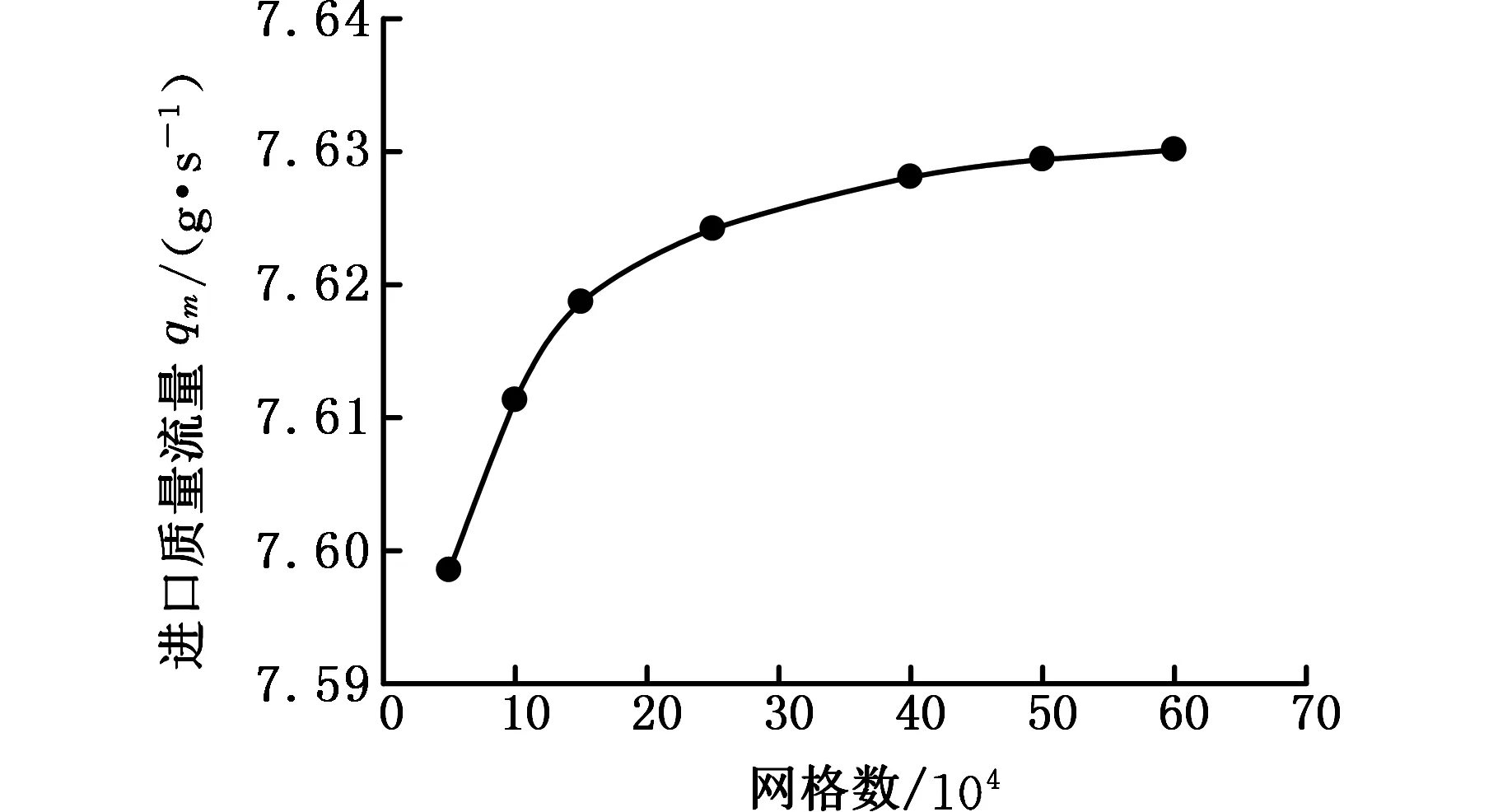
图2 网格无关性检查Fig.2 Grid independence check

1.2 湍流模型、流体物性及边界条件

本文通过商业软件ANSYS Fluent12.0计算7种湍流模型下的直角转弯流场，并将计算结果与实验结果进行对比，计算采用非耦合隐式方案进行求解，通过有限体积法进行空间离散，对控制方程中的源项和扩散项应用二阶中心差分格式，对流项应用二阶迎风格式。

为保证实验阀块的流场特性与原型阀块相同，实验阀块的几何及工作参数经过雷诺相似计算确定[10]，数值计算边界条件设定与实验阀块保持一致，给定速度入口、压力出口边界条件，具体数值如表1所示。

表1 数值计算参数设置Tab.1 Parameter selection of numerical calculation model

2 模拟结果及分析

图3将计算模拟和实验测量得到的A涡、B涡的涡核位置绘制到统一坐标系中。结果表明，各种湍流模型计算的A涡、B涡的涡核位置与实验结果均存在差别。对于出流方向正对刀尖角容腔模型，S-A模型计算的A涡、B涡的涡核位置相比于其他湍流模型模拟更接近实验结果；对于入流方向正对刀尖角容腔模型，可实现的k-ε模型预测的A涡位置与实验最为接近，标准k-ω模型预测的B涡位置与实验最为接近，而S-A模型对A涡和B涡涡核位置的预测结果较差。

为了能定量比较各湍流模型对两种模型中两个涡核位置的综合预测精度，本文定义了权重误差函数K，表达式如下：

K=70%KA+30%KB

式中，KA为A涡涡核计算位置与实验测量位置的绝对距离；KB为B涡涡核计算位置与实验测量位置的绝对距离。

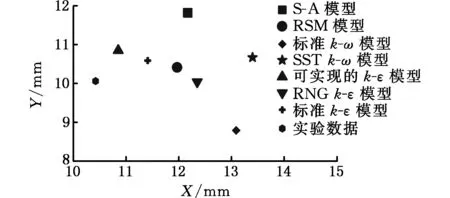
(a)入流方向正对刀尖角容腔A涡的涡核位置

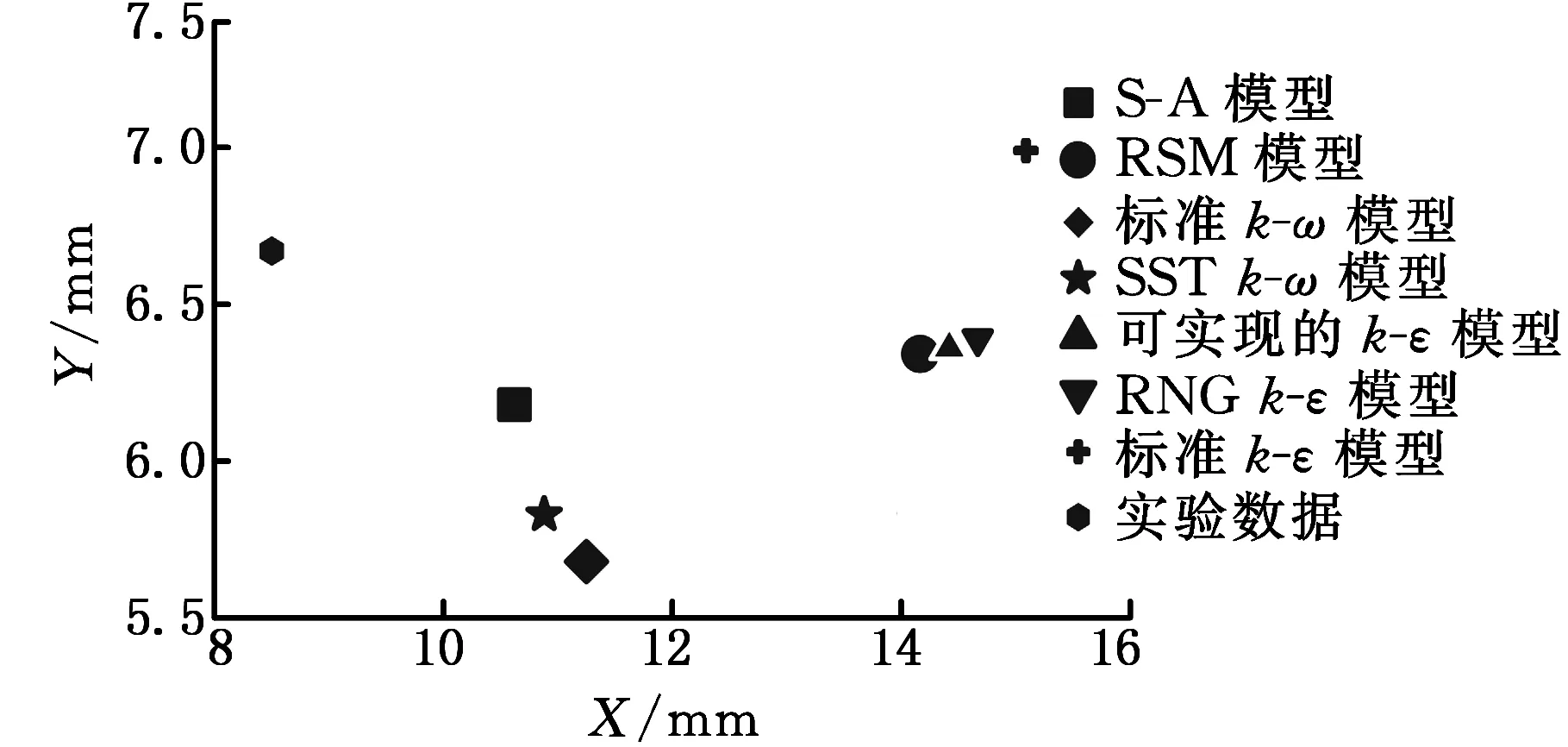
(b)出流方向正对刀尖角容腔A涡的涡核位置

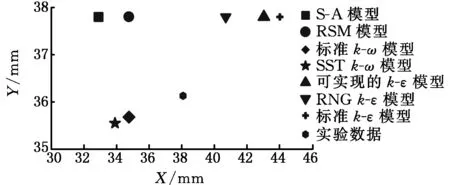
(c)入流方向正对刀尖角容腔B涡的涡核位置

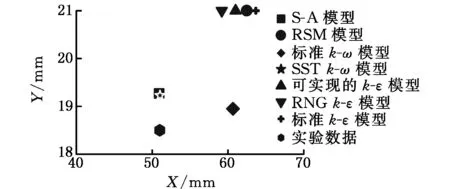
(d)出流方向正对刀尖角容腔B涡的涡核位置图3 A涡、B涡的涡核位置比较Fig.3 Comparison of vortex core positions between A and B vortices

考虑到A涡是带刀尖角容腔直角转弯流道的最主要流动特征，因此取A涡的涡核位置预测精度权重为70%，B涡的涡核位置预测精度权重为30%。

表2计算了7种湍流模型下入流方向正对刀尖角容腔模型的权重误差K。结果表明各湍流模型计算的权重误差K差别不大，其中最优的是二方程的可实现的k-ε模型，七方程的RSM模型预测结果也较好，S-A模型的预测结果较差。

表3计算了出流方向正对刀尖角容腔模型的权重误差K。计算结果表明，各湍流模型计算的权重误差K差别较大，S-A模型的预测结果最优，其K值仅为1.76，二方程模型中SSTk-ω模型计算结果也较优，七方程的RSM模型的预测结果误差较大，而被认为通用性最好的标准k-ε模型的计算结果是最差的。

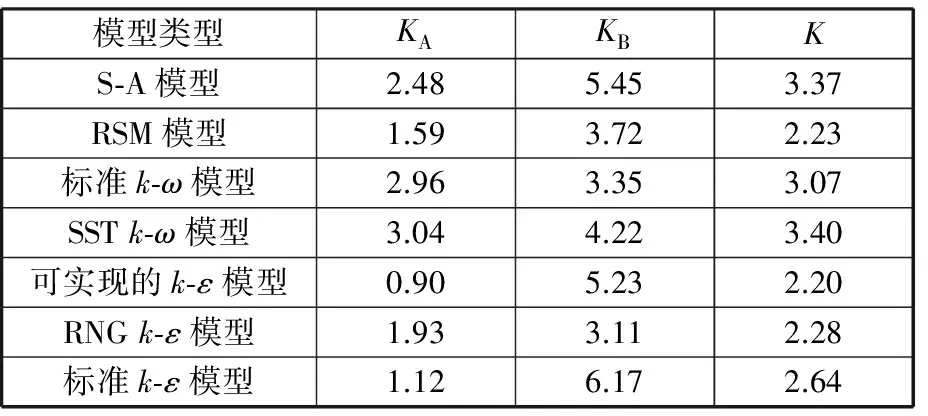
表2 入流方向正对刀尖角模拟误差Tab.2 Simulation error of Inflow face the right angle cavity

表3 出流方向正对刀尖角模拟误差

Tab.3 Simulation error of outflow face theright angle cavity

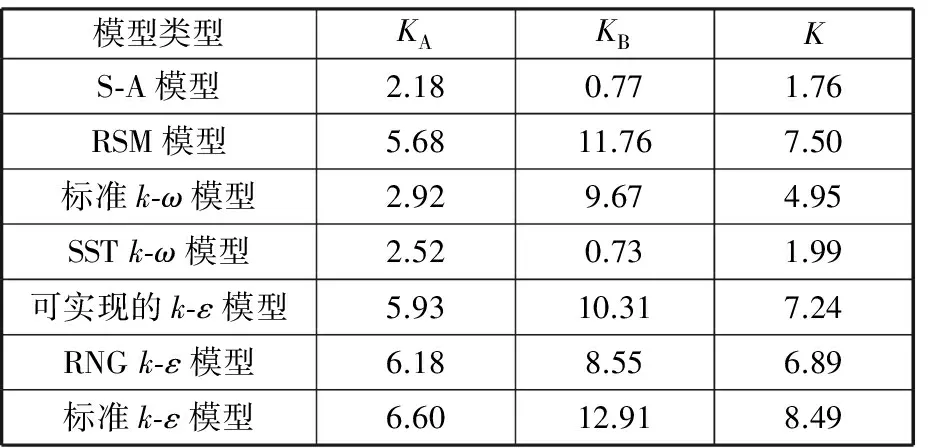
模型类型KAKBKS⁃A模型2．180．771．76RSM模型5．6811．767．50标准k⁃ω模型2．929．674．95SSTk⁃ω模型2．520．731．99可实现的k⁃ε模型5．9310．317．24RNGk⁃ε模型6．188．556．89标准k⁃ε模型6．6012．918．49

考虑到计算代价和计算精度的平衡，笔者认为采用一方程S-A模型作为基础湍流模型进行修正是合适的。后文对S-A模型中的湍流输运参数进行适当修正，以期进一步提高对直角转弯型流道的流场预测精度。

3 S-A湍流模型修正

3.1 S-A模型简介

S-A湍流模型以其形式简单、数值稳定性和收敛性好、计算精度不亚于高阶模型等特征获得了相当成功的应用[11]，其输运方程的表达式如下：

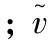
湍流黏性的生成项Gν以及耗散项Yν在输运过程中起主要作用，它们的差值反映了湍流的非平衡特性[12],而正确预估湍流黏性的生成和耗散的关系是改进湍流模型的关键。

大量研究表明，传统的S-A模型对分离流动的流场细节预测能力较差，而流体在直角转弯的过程中存在大范围的流动分离，此时的湍流恰好处于强非平衡状态。研究表明，影响输运方程中的湍流黏性生成项Gν以及耗散项Yν的最重要参数为Cb1[13]，改变Cb1值可以较好地调整生成项和耗散项的关系,因此，本文将通过修正Cb1来改进S-A湍流模型的流场预测性能。

3.2 S-A模型修正

图4计算了7组Cb1参数对应的权重误差K。结果表明，对于入流方向正对刀尖角容腔模型，Cb1存在最优值，当取值为0.25时，权重误差函数值最小；对于出流方向正对刀尖角容腔模型，增大Cb1权重误差值逐渐增大，预测效果变差，两者之间存在此消彼长的关系。综合来看，当Cb1取两变化曲线的交点处的值(Cb1=0.17)时，S-A模型对出流、入流方向正对刀尖角容腔模型流场的综合预测精度最好。

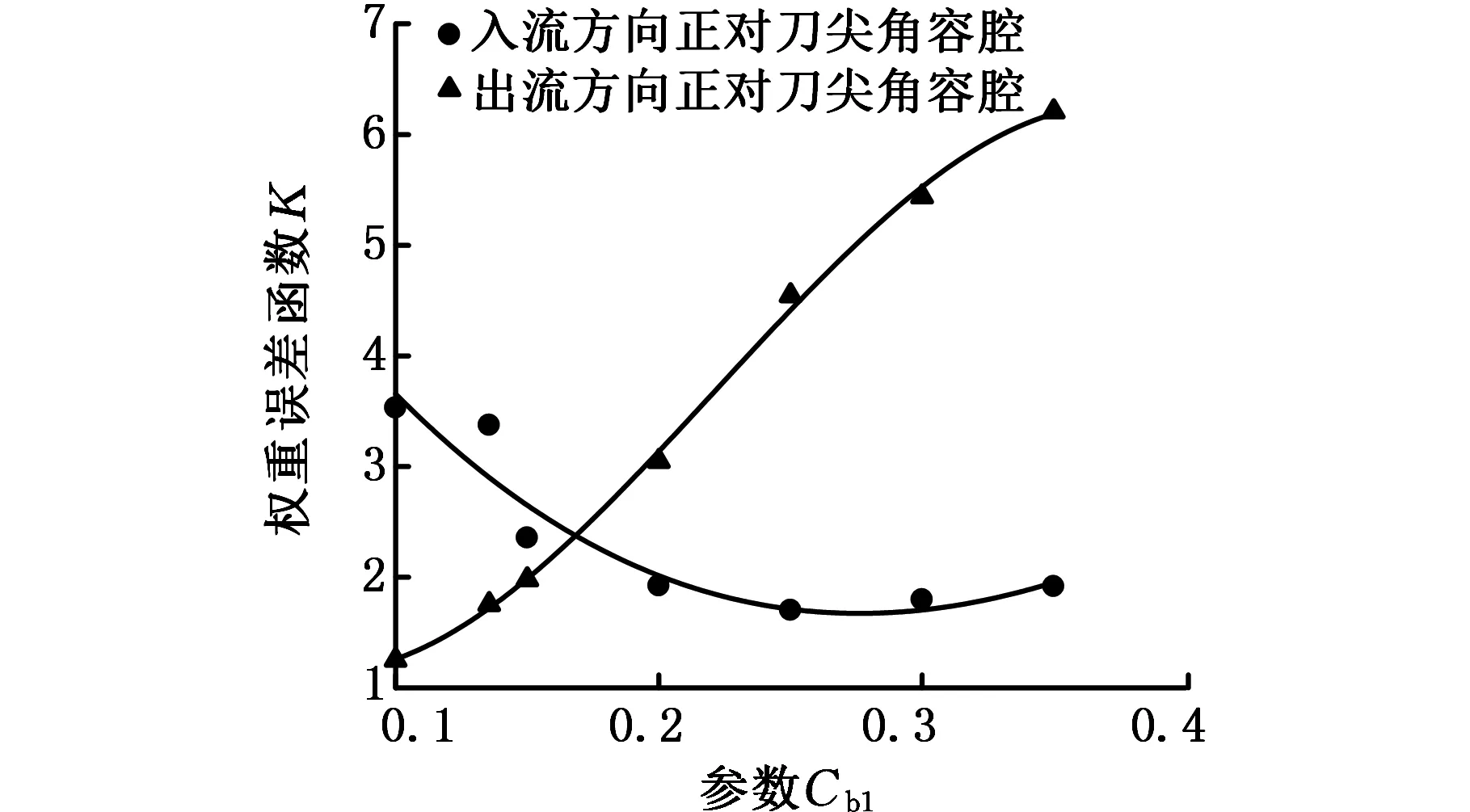
图4 不同Cb1模拟结果权重误差的拟合曲线Fig.4 Fitting curves of K under different Cb1

与S-A模型Cb1的原始设置值0.1355相比，采用修正值0.17后，对于入流方向正对刀尖角容腔模型，修正后A涡、B涡的涡核位置预测精度分别提高了3%和59%，权重误差函数值K降低34.72%；对于出流方向正对刀尖角容腔模型，修正后A涡的涡核位置预测精度降低了15%，B涡的涡核位置预测精度提高了2.6%，权重误差函数值K增加了25.0%。以上结果表明，修正时牺牲了一个旋涡位置的预测精度，但总体预测精度得到改善。

4 典型直角转弯流道内流特性分析

下文采用经修正的S-A湍流模型，对液压集成块中三种典型的直角转弯流道进行流场仿真，探讨不同速度下各典型流道压力损失特性。考虑到增材制造技术在工业应用上的发展与普及，本部分将圆弧过渡直角转弯流道模型(转弯半径为20 mm)也进行了建模和仿真计算，并与上述三种进行对比。

为准确描述直角转弯流道的流动损失的情况，定义总压损失系数

式中，Δp为进口总压与当地总压差,Pa；ρ为液流密度,kg/m3；v为液流速度,m/s。

图5为4种典型的直角转弯流道(圆弧过渡型、双侧刀尖角型、出流正对刀尖角型、入流正对刀尖角型)在同一速度下流道中截面的流线分布和总压损失系数分布云图。通过流线分布比较可知，圆弧过渡型流道的流线平滑无明显旋涡，高总压损失区的范围最小，预期具有最小的流动损失；

(a)圆弧过渡直角转弯流道

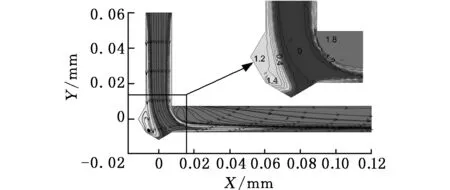
(b)双侧刀尖角直角转弯流道

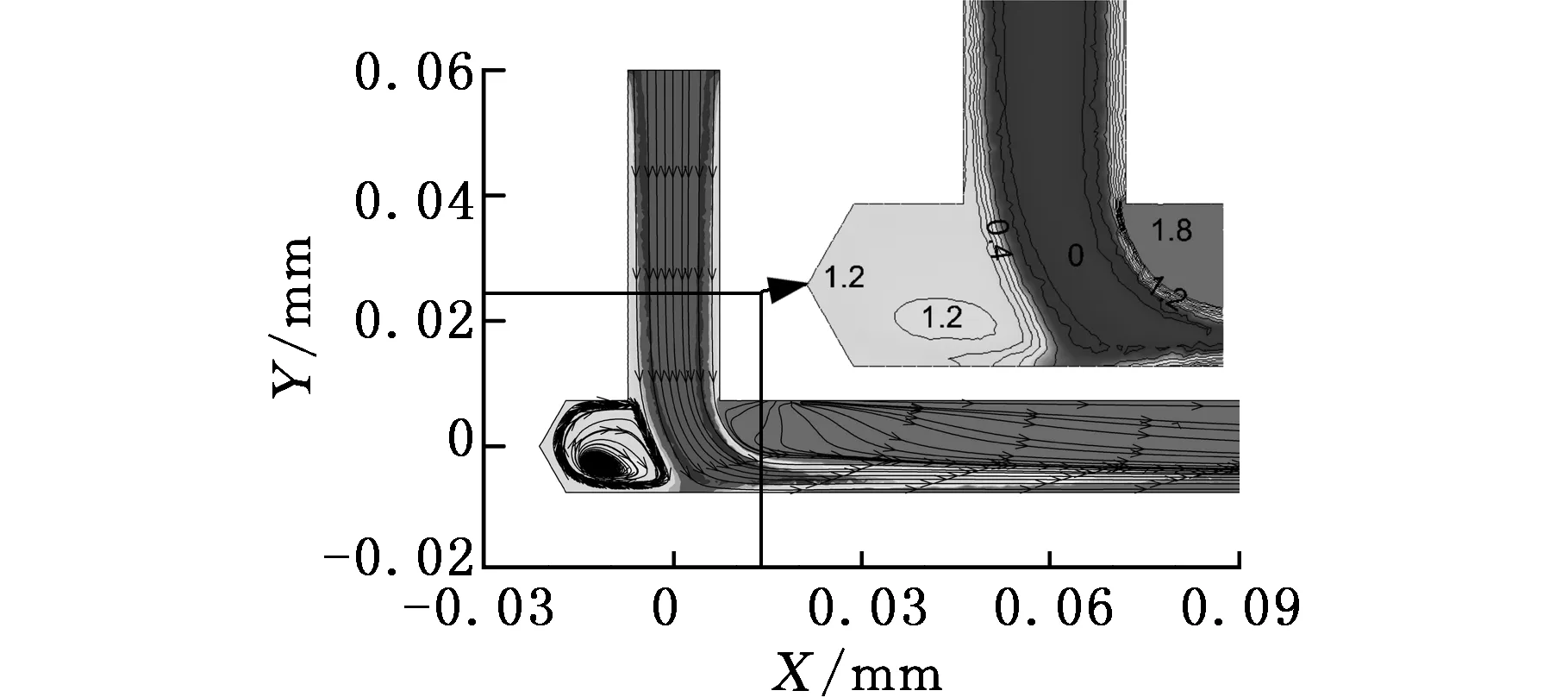
(c)出流正对刀尖角直角转弯流道

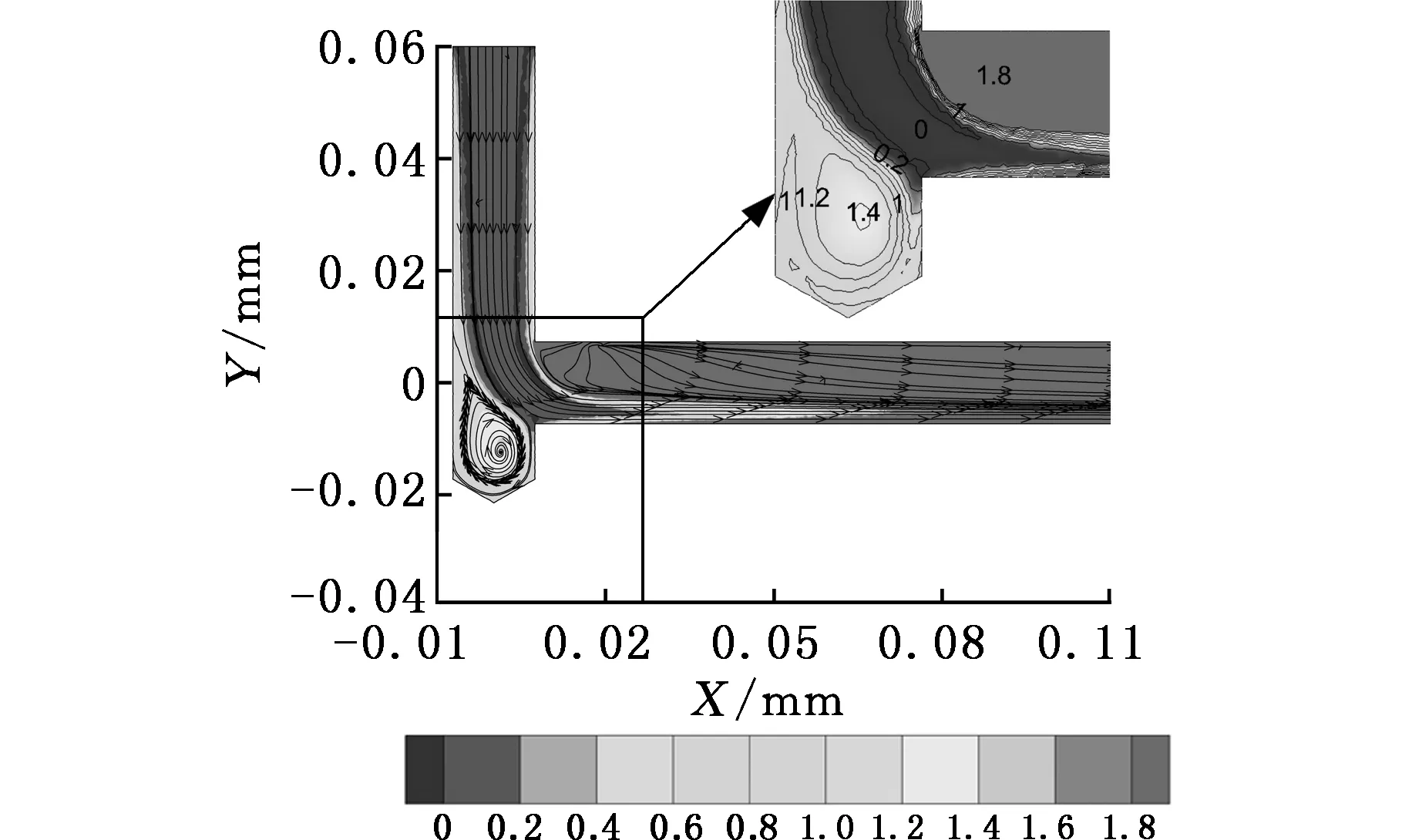
(d)入流正对刀尖角直角转弯流道图5 速度流线总压损失系数分布云图Fig.5 Distribution contours of streamlines and total pressure loss coefficients

其余三种带有刀尖角容腔的直角转弯流道，在刀尖角内均存在显著旋涡，对应着一个高总压损失区，同时由于采用直角过渡，过弯后的二次流损失较为剧烈，表现为过弯后大范围的高总压损失区。

图6基于进出口总压差，计算了上述4种典型直角转弯流道在不同速度下的量纲一总压损失系数的变化规律。结果表明，4种流道形式的总压损失系数随进口速度增加呈逐渐下降的趋势，但差值基本维持稳定。其中，圆弧过渡型流道的总压损失系数始终远小于其余三种带有刀尖角容腔的转弯流道，即具有最小的流动损失。在计算工况范围内，与带有刀尖角容腔的流道相比，圆弧过渡型流道的总压损失系数有68%～72%的降低，流动损失下降非常显著。对于目前在液压集成块流道加工中常见的带有刀尖角容腔流道，出流方向正对刀尖角型流道具有更小的流动损失，这与文献[10]关于带有刀尖角容腔流道流动损失机理分析的结论一致。双侧带有刀尖角容腔的流道形式总压损失系数最高，在液压集成块流道加工中应尽量避免。

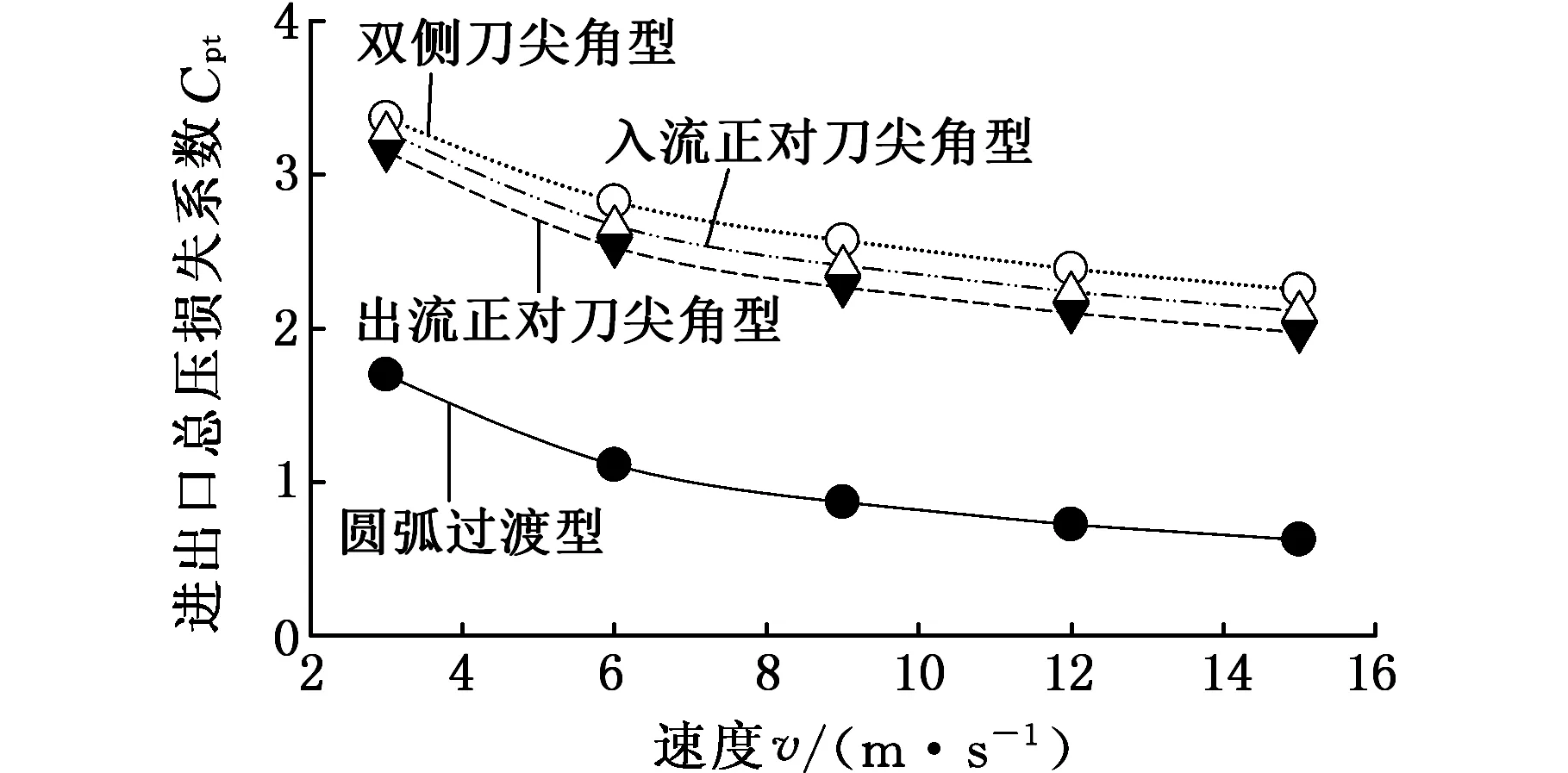
图6 典型转弯流道进出口总压损失系数变化曲线Fig.6 Variation curve of total pressure loss coefficient under different inlet velocity

5 结论

(1)通过定义权重误差函数K来定量比较各湍流模型对不同模型中不同涡核位置的综合预测测精度，综合考虑预测精度和计算代价，选定S-A模型作为待修正的基础湍流模型。

(2)计算表明当Cb1取0.17时，S-A模型对出流正对刀尖角容腔模型权重误差值上升25.0%，入流正对刀尖角容腔模型权重误差值下降34.7%，修正后的S-A模型对带有刀尖角容腔直角转弯流场的综合预测精度有所提高。

(3)圆弧过渡型直角转弯流道相比于带有刀尖角容腔的流道具有更小的总压损失，在计算工况范围内，总压损失系数有68%～72%的降低。

[1] 黄人豪. 基于MINISO紧凑型二通插装阀的新一代模块化、可配组和开放式电-液组合式控制技术[J]. 液压气动与密封,2012(1):78-81. HUANG Renhao.Based on MINISO Compact Two-way Cartridge Valves, a New Generation of Modular, with the Group and Open Electric-Hydraulic Control Technology Combined[J]. Hydraulic Pneumatic and Sealing,2012(1):78-81.

[2] 田树军, 张宏, 李利. 液压集成块管网动态特性仿真[J]. 机床与液压,2007,35(4):196-200. TIAN Shujun, ZHANG Hong, LI Li.Dynamic Characteristic Simulation of Pipeline Network in HMB[J]. Machine Tools and Hydraulic,2007,35(4):196-200.

[3] 张宏, 田树军, 刘万辉, 等. 基于CFD的液压集成块典型流道液阻仿真研究[J].中国机械工程,2007,18(18):2223-2226. ZHANG Hong, TIAN Shujun, LIU Wanhui, et al. Research on CFD-based Simulation of Typical Flow- resistance in HMB Pipeline[J]. China Mechanical Engineering,2007,18(18):2223-2226.

[4] 雷琪, 王自勤, 田丰果, 等. 液压集成块流道数值模拟分析[J]. 现代制造、工艺装备,2016(1):19-22. LEI Qi, WANG Ziqin, TIAN Fengguo, et al. Numerical Simulation Analysis of Pipeline of Hydraulic Manifold Block[J]. Modern Manufacturing and Process Equipment,2016(1):19-22.

[5] 杜经民, 蔡保全, 李宝仁. 某系统液压集成块流道液流特性分析[J]. 机床与液压,2010,38(13):143-146 DU Jingmin, CAI Baoquan, LI Baoren. Analysis for Flowing Characteristics of Fluid Inside Hydraulic Manifold Block Channels of a Certain System[J]. Machine Tools and Hydraulic,2010,38(13):143-146.

[6] 谢国庆, 李运初. 基于Fluent 的液压集成块典型流道流场仿真分析[J].液压与气动,2013(12):44-46. XIE Guoqing, LI Yunchu. Simulation and Analysis for Flow Field of Typical Channel inside Hydraulic Manifold Block Based on Fluent[J]. Hydraulic and Pneumatic,2013(12):44-46.

[7] 吴正坤, 赵毅红, 吕宵宵, 等. 基于Fluent液压集成块内部流场数据仿真[J]. 机械工程与自动化,2014(6):76-80. WU Zhengkun, ZHAO Yihong, LYU Xiaoxiao, et al. Fluent-based Numerical Simulation of Internal Flow Field of Hydraulic Manifold[J]. Mechanical Engineering and Automation,2014(6):76-80.

[8] 苏乃权, 李石栋, 蔡业彬, 等. 基于 FLUENT 的集成块流道的仿真分析[J]. 机床与液压, 2017,45(4):92-109. SU Naiquan, LI Shidong, CAI Yebin, et al.Manifold Block Flow Simulation Analysis Based on Fluent[J]. Machine Tool and Hydraulics, 2017,45(4):92-109.

[9] 丁珏, 翁培奋. 90°弯管内流动的理论模型及流动特性的数值研究[J]. 计算力学学报, 2004,21(3):314-321. DING Jue, WENG Peifen. The Numerical Study of Theoretical Model and Flow Characteristics of 90°Bend Pipe[J]. Chinese Journal of Computational Mechanics,2004,21(3):314-321.

[10] 胡建军, 孔祥东, 侯冠男, 等. 刀尖角容腔对直角转弯流道液流特性影响的PIV实验研究[J]. 中国机械工程,2015,26(7):943-948. HU Jianjun, KONG Xiangdong, HOU Guannan, et al. Experimental Investigation of Flow Characteristics of Right-angle Turn with Different Tool Included Angle Using 2D-PIV Technique[J]. China Mechanical Engineering,2015,26(7):943-948.

[11] SPALART P, ALLMARAS S. A One-equation Turbulence Model for Aerodynamic Flows[R]. Seattle, WA: Boeing Commercial Airplane Group,1992.

[12] MANSOUR N N, KIM J, MOIM P. Reynolds-stress and Dissipation-rate Budgets in a Turbulent Channel Flow [J]. Fluid Mech., 1988,194:15-44.

[13] 王丹华, 陆利蓬, 李秋实. 基于湍流输运特性对S-A模型在压气机角区流动模拟中的改进研究[J]. 航空动力学报,2010,25(1):80-86. WANG Danhua, LU Lipeng, LI Qiushi. Improvement on S-A Model for Compressor Flow Based on Turbulence Transport Nature[J]. Journal of Aerospace Power,2010,25(1):80-86.

(编辑 袁兴玲)

Turbulence Model Correction and Internal Flow Characteristics Analysis of Hydraulic Manifold Blocks

HU Jianjun1,3CHEN Jin3QUAN Lingxiao1,2ZHANG Jin1,2KONG Xiangdong1,2

1.School of Mechanical Engineering, Yanshan University, Qinhuangdao,Hebei,0660042.Engineering Research Center of Advanced Forging & Stamping Technology and Science Built byCentral Government and Local Government, Yanshan University, Qinhuangdao,Hebei,0660043.School of Civil Engineering and Mechanics, Yanshan University, Qinhuangdao,Hebei,066004

A corresponding numerical calculation model was established and the three-dimensional flow field simulation was carried out based on the particle image velocimetry (PIV) measurements of the flow fields of right-angle turn channels with cavities. The predictive ability of the 7 kinds of turbulence models commonly used in engineering were investigated by comparison the typical vortex structure of numerical results. By defining the weight error functionK, a S-A model was selected as the basic turbulence model and were modified. The results show that when the S-A model Cb1is modified from the default value 0.1355 to 0.17, the weight errors of the outflows facing to the right angle cavity model increase by 25.0%, and the weight errors of the inflows facing to the right angle cavity model decrease by 34.7%. In general, the predictive accuracy of modified S-A turbulence model is improved in forecasting the flow fields of two kinds right-angle turn channels with cavities. The internal flow characteristics of four typical right angle channels were analyzed by using the modified S-A turbulence model, the results show that the arc right angle flow passages have smaller pressure losses than that of the turning flow channels with cavities.

hydraulic manifold block； turbulence modle；right-angle turn channel；flow characteristics

2016-12-09

国家自然科学基金资助项目(51641508)；河北省自然科学基金资助项目(E2015203271)； 燕山大学青年教师自主研究计划资助项目(14LGA014)；燕山大学博士基金资助项目(B912)

TH137

10.3969/j.issn.1004-132X.2017.14.012

胡建军,男，1982年生。燕山大学机械工程学院博士，建筑工程与力学学院副教授。主要研究方向为流体传动与控制。E-mail:kewei729@163.com。陈 进，男，1992年生。燕山大学建筑工程与力学学院硕士研究生。权凌霄，男，1976年生。燕山大学机械工程学院副教授。张 晋，1984年生。燕山大学机械工程学院讲师。孔祥东，男，1959年生。燕山大学，机械工程学院教授、博士研究生导师。