基于RBF神经网络的隧道掘进机推进自适应PID控制

宋立业 万应才

辽宁工程技术大学电气与控制工程学院，葫芦岛，125105



基于RBF神经网络的隧道掘进机推进自适应PID控制

宋立业 万应才

辽宁工程技术大学电气与控制工程学院，葫芦岛，125105

针对全断面隧道掘进机的推进压力和推进速度的匹配问题，应用RBF神经网络算法设计了使推进压力和推进速度匹配且推进速度能快速跟随设定目标的自适应控制器。先在MATLAB中建立推进控制系统仿真模型，分析控制器自适应控制效果，然后在AMESim中建立推进系统液压控制模型，并与MATLAB联合仿真。联合仿真验证该控制器能在刀盘负载压力波动突变的情况下，使刀盘推进速度和推进压力跟随设定目标。试验证明，该控制器对负载大范围扰动有很好的抑制能力，能明显提高推进速度和推进压力耦合度并减小两者的波动范围。

全断面隧道掘进机；液压控制；自适应控制；大扰动

0 引言

隧道掘进机(tunnel boring machine，TBM)利用旋转刀盘的滚刀挤压剪切破岩，通过旋转刀盘铲斗收集石渣，并由皮带运输到洞外。TMB掘进过程中，刀盘的总推力和总扭矩影响刀具贯入岩石的深度、切削载荷、刀具磨损、刀盘主轴寿命[1]。推进速度和推进压力是刀盘推进总压力和总扭矩的主要影响因素，直接影响TBM的掘进效率。刀盘破岩时，刀盘负载会发生较大变化，推进油缸的压力和速度随之发生较大波动。隧道掘进过程中，推进控制器需要在岩石硬度不断变化、地层条件复杂、刀盘载荷不平衡等环境下精确控制推进压力和推进速度，保证掘进效率。

胡国良等[2]建立的缩尺TBM试验台能在负载变化时，单独调节推进速度和推进压力达到设定值；施虎等[3]将单神经元应用到推进PID控制中，有效消除了推进过程中液压系统及负载的非线性因素的影响。

当前，推进控制的研究主要集中在对刀盘推进速度的控制，以设定的固定推进速度为控制目标，以推进油缸位移和压力为反馈信号，通过控制策略调节达到跟随设定目标。目前的研究没有对推进压力和速度互相影响的因素进行分析，在岩石硬度过大、推进油缸推进速度降低的情况下，传统的速度控制器仍使推进油缸速度增加，导致推进速度调节波动过大，影响工作效率。

本文基于推进液压控制系统模型，在Simulink中将推进油缸压力和推进速度作为控制器输入，将推进油缸压力反馈作为调节推进速度的参考，利用径向基函数(RBF)神经网络对PID控制在线整定，调节推进油缸压力和速度。在调速阀和溢流阀控制中利用PID控制，根据流量和压力返回值，实时控制比例调速阀和比例溢流阀开度，使推进油缸的推进速度和控制器设定速度保持一致，在液压仿真环境下验证建立传递函数的正确性和控制器的控制效果。最后在全断面硬岩掘进机KSZ-2600上，通过西门子S7-300PLC控制器进行了验证。

1 全断面硬岩掘进机推进系统

1.1 全断面硬岩掘进机工作过程

全断面硬岩掘进机如图1所示，首先掘进机的推进油缸收回，然后前后2对撑靴伸出挤压岩壁，后支撑收回，以上动作完成之后，掘进机处于开始掘进状态。刀盘开始转动时，以撑靴挤压岩为支撑点的推进油缸伸出，使刀盘向前移动，刀盘上的刀具在转动过程中贯入岩石，对岩石进行挤压剪切破碎[3]。推进油缸达到设定伸出长度后，推进过程完成，此时后支撑伸出，挤压岩壁的前后撑靴收回，由于刀盘质量大，推进油缸前端静止，推进油缸收回时带动其后部连接的前后2对撑靴前移，撑靴再次伸出挤压岩壁，后支撑收回，掘进机恢复到开始掘进前的初始状态，依次进行下一循环。

图1 全断面硬岩掘进机三维模型Fig.1 3D model of full cross section tunnel boring machine

1.2 全断面硬岩掘进机推进液压系统原理

图2所示的全断面液压掘进机推进系统由油泵2供油，三位四通电磁换向阀4打开时，通过调节比例调速阀3，使推进油缸7的无杆腔内大量进油，同时控制比例溢流阀5，使推进油缸无杆腔内压力增大，推动刀盘前进。压力传感器6和位移传感器8检测推进油缸压力和伸出位移，经过控制器调整，然后输出调节比例溢流阀和比例调速阀的输入信号，对液压控制系统进行调节[4]。

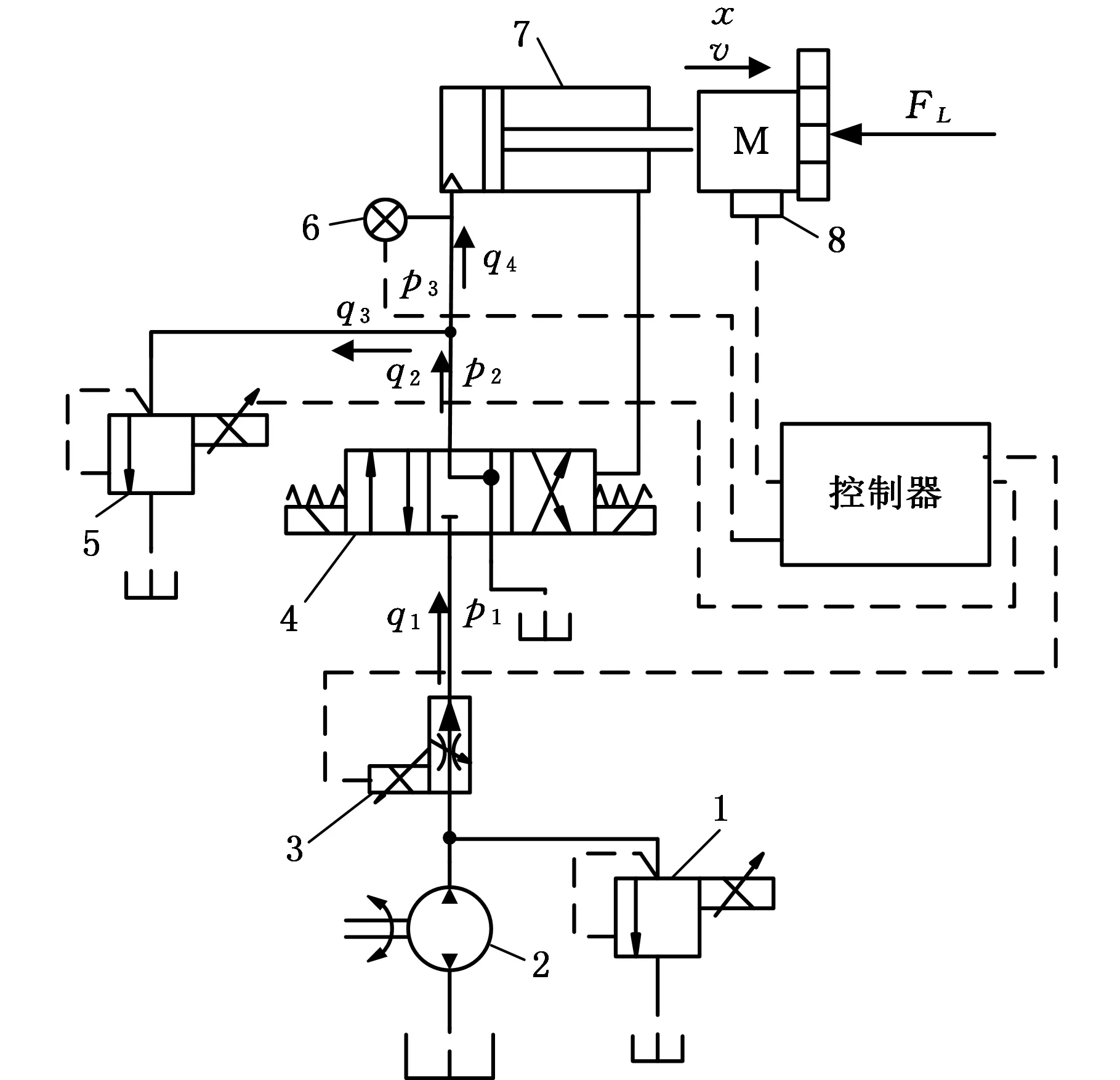
1.溢流阀 2.油泵 3.比例调速阀 4.三位四通电磁换向阀 5.比例溢流阀 6.压力传感器 7.推进油缸 8.速度传感器图2 全断面液压掘进机推进液压控制原理图Fig.2 Full cross-section hydraulic boring machine to promote hydraulic control schematic

1.3 全断面硬岩掘进机掘进数据分析

KSZ-2600型全断面快速硬岩掘进机以西门子S7-300 PLC为主控器，对推进速度和推进压力单独PID控制。KSZ-2600掘进时间内的推进速度、推进压力及刀盘转速的掘进数据如图3所示。

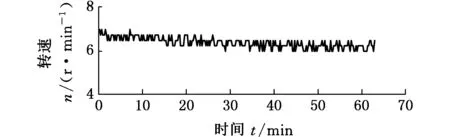
(a)刀盘转速

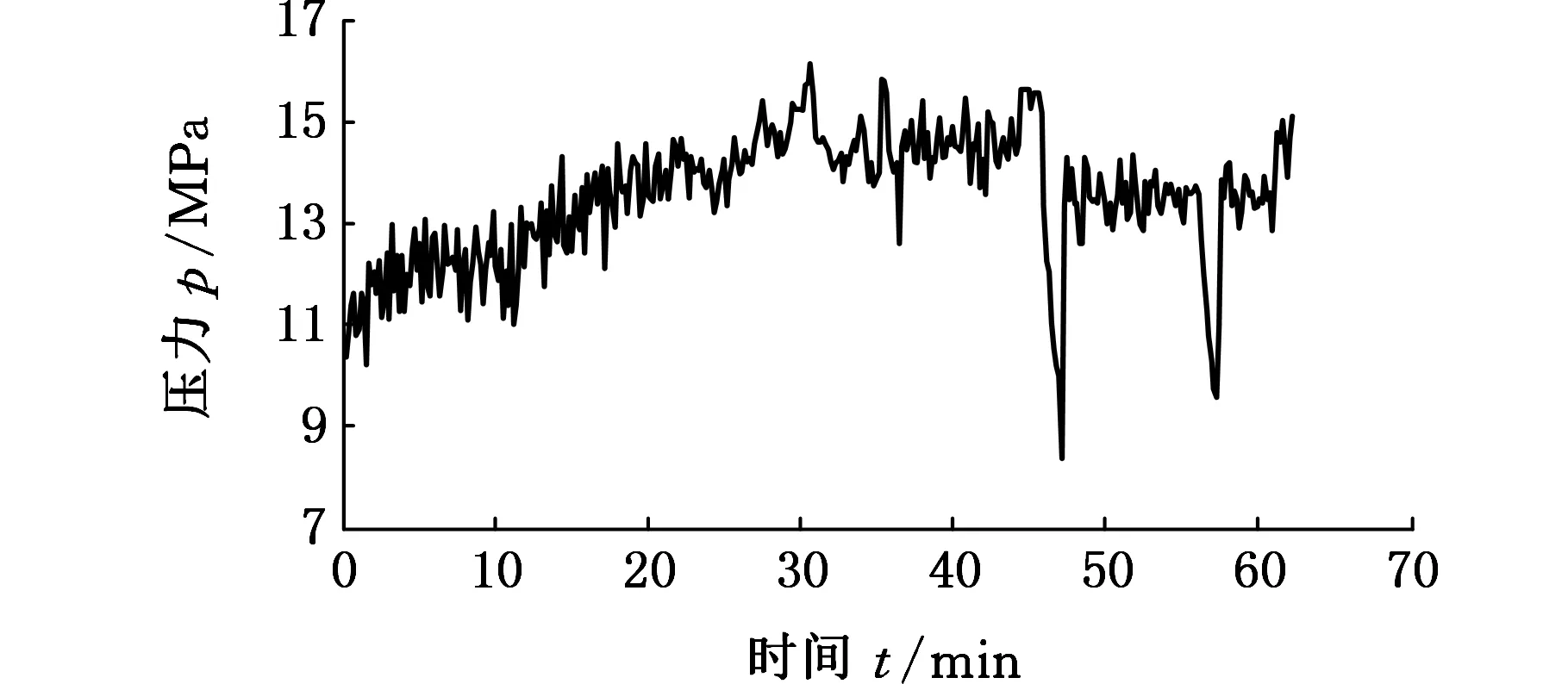
(b)推进压力

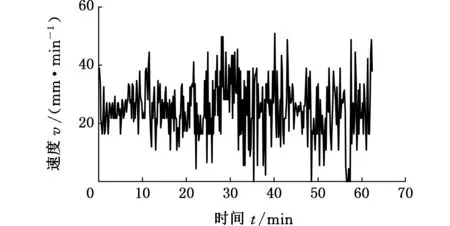
(c)推进速度图3 KSZ-2600掘进历史数据Fig.3 KSZ-2600 excavation history data

通过分析上述数据可知，在掘进过程中，刀盘转速在6～7.5 r/min内波动，推进速度在5～50 mm/min内波动。全断面掘进机单独以速度为控制量时，若推进压力比较大，则推进速度比设定值下降明显，此时控制器经PID调节的输出增量增大，使速度继续升高。随着掘进的进行，当刀盘前方压力释放后，推进速度比设定值高出很多，控制器控制的液压油缸推进速度调量增大。由于传感器采样频率和液压系统的滞后性，误差大范围调整会导致推进速度和推进压力波动范围变大。全断面掘进机在推进压力和推进速度波动较大的条件下长期工作，会带来掘进时间和刀具寿命缩短、核心机械结构部件损坏等一系列问题。

针对以上实际掘进面临的问题，将推进压力在单位时间内的平均值作为推进压力与推进速度联合控制的一个控制量输入。当推进压力大于设定压力时，保持推进速度控制器控制增量不变；反之，推进速度则由RBF-PID控制。

2 推进系统建模

推进过程中，比例调速阀在稳定工作情况下，调速阀的输出流量即节流阀阀口处的流量方程[5]为

q2=kq2y2

(1)

式中，q2为节流阀出口的流量，L/min；kq2为流量增益；y2为节流阀阀芯位移，mm。

节流阀的运动方程为

(2)

式中，FM2为比例电磁铁在给定电流时产生的推力，N；m为节流阀阀芯质量，kg；D2为黏性摩擦系数，N·m/s；K2为节流阀等效弹簧刚度，N/m。

如果溢流阀出口直接接油箱，压力近似为零，则通过锥阀阀口处的流量方程为

q3=kq3y3+kp3pL

(3)

式中，q3为锥阀阀口处的流量，L/min；y3为节流阀阀芯位移，m；kq3为流量增益；kp3为流量-压力系数；pL为负载压力，MPa。

假定液压缸工作腔内各处压力相同，油液温度和体积弹性模量可认为是常数，液压缸内泄漏为层流流动。此时液压缸的流量连续性方程可表示为

(4)

式中，A为液压缸活塞作用面积，m2；x为活塞的位移，m；Ctc为黏滞阻尼系数，N·m/s；V为液压缸高压腔及进油管路油液体积，m3；E为油液体积弹性模量，Pa。

液压缸的动态方程为

(5)

式中，M为移动部件的总质量，kg；BV为弹簧的阻尼系数，m3/(Pa·s)；FL为作用在活塞杆上的外加负载力，N；k为弹簧负载刚度。

当输入一定的电压时，动态方程为

(6)

式中，U(t)为给定电压，V；L为电感，H；I为电流，A；R为电阻，Ω；kv为位移返回增益系数。

比例电磁铁内部的线圈可以把电流转化成力，比例溢流阀的先导阀的传递函数为

FM=KFI

(7)

式中，FM为线圈产生的电磁力，N；KF为电流与力的增益系数。

通过以上的分析和推导，分别得出推进系统的比例调速阀、比例溢流阀、推进液压缸、负载的传递函数，根据现场的实际参数赋值，进而得到实际的模型。比例调速阀[6]的传递函数为

(8)

比例溢流阀的先导阀的传递函数[7]为

(9)

k1=ksy+a0kpyk2=2ζy(ksy+a0kpy)

式中，wy为先导阀面积增益，wy=3.78 mm；ksy为衔铁组件等效弹簧刚度，ksy=2921 N/m；kpy为先导阀口的压力增益，kpy=47.4 MPa/cm；A0为先导阀流通面积，A0=2.54 mm2；fm为先导级固有频率，fm=493 Hz；ζm为先导级阻尼系数，ζm=0.8。

比例溢流阀的主阀传递函数为

(10)

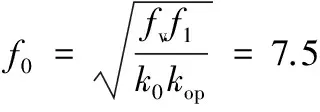
式中，fv为主阀运动主导折转频率，fv=3.4 Hz；f1为阀前管路固有频率，f1=8.1 Hz；kop为主阀流量压力系数，kop=29.4 MPa·s/cm3。

推进液压缸的传递函数[8]为

(11)

负载的传递函数为

(12)

3 RBF神经网络PID控制算法

RBF网络是一种用于解决模式分类的三层前馈网络，包括输入层、隐含层和输出层[9]。输入层到隐含层之间的权值固定为1，即输入层对信息不作任何处理，仅仅将输入变量分配给隐含层，隐含层的一个神经元代表一个径向基函数。隐含层到输出层的权重可调。隐含层节点由像高斯基函数那样的辐射状作用函数组成，其节点数不需要像 BP网络那样进行预先设定，而是在学习过程中不断增加，直到满足误差指标为止。RBF的输出层节点通常是简单的线性函数。基于RBF网络整定的PID控制由RBF神经网络辨识器和 PID控制器两部分组成。RBF神经网络辨识器通过被控对象的输入输出数据辨识出被控对象的近似模型，并以此代替被控对象的输入输出关系。PID控制器的参数通过 RBF神经网络辨识器实现自适应整定。在RBF网络辨识器结构中，X=(x1，x2，…，xn)为网络的输入向量。设RBF网络的径向基向量H=(h1，h2，…，hn)，hj(j=1，2，…，m)为高斯基函数，可得

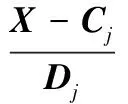
网络的第j个节点的中心矢量Cj=(c1j，c2j，…，cnj) ，设网络的基宽度向量Dj=(d1，d2，…，dm)，其中，dj为节点j的基宽度参数，dj>0。网络的权向量为

W=(w1，w2，…，wm)

辨识网络的输出为

ymout(k)=w1h1+w2h2+…+wmhm

辨识器的性能指标函数为

J1=(yout(k)-ymout(k))2/2

TBM动作时，对其控制精度要求不是特别高，因此对控制精度要求不是特别高的部分可以通过网络参数以及权值调整来修正。控制器为增量式PID控制器，控制误差为

e(k)=rn(k)-yout(k)

神经网络整定指标为

E(k)=e2(k)/2

增量式PID算法[10]的表达式为

Δu(k)=kp(e(k)-e(k-1))+kie(k)+

kd(e(k)-2e(k-1)+e(k-2))

其中，kp、ki、kd的调整采用梯度下降法，即

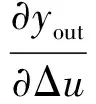
4 MATLAB仿真分析

如图4所示，将设定的推进速度与实时检测的推进油缸速度进行比较，并将产生的误差送入RBF-PID控制器，RBF训练并不断调整PID中参数，使系统在误差范围内跟随设定速度。同时检测推进油缸压力，如果推进油缸压力达到设定压力上限，则通过速度压力调节，减小给定速度，避免推进过程中刀盘前方压力过大时，依然增大推进速度调整增量，使控制推进速度持续增大。

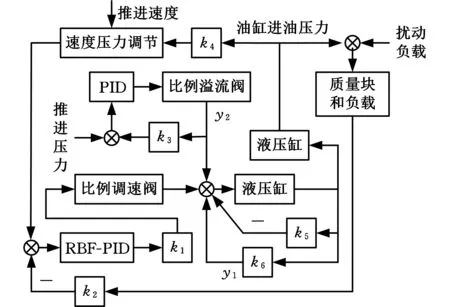
图4 推进控制系统框图Fig.4 Block diagram of propulsion control system

根据图4，在MATLAB Simulink搭建的仿真模型中进行仿真实验。在负载保持不变的情况下，推进油缸推进速度设定值为0.8 mm/s，经过控制器控制[11]，使推进油缸伸出速度达到设定的0.8 mm/s，并保持稳定。在负载不发生变化时，推进速度响应曲线如图5所示；在4 s时，施加50 kN扰动负载，如图5所示，在负载发生扰动的情况下，控制器依然能使系统快速稳定，达到设定速度。

图 5 有无负载扰动时推进速度控制Fig.5 Propulsion speed control with and without load disturbance

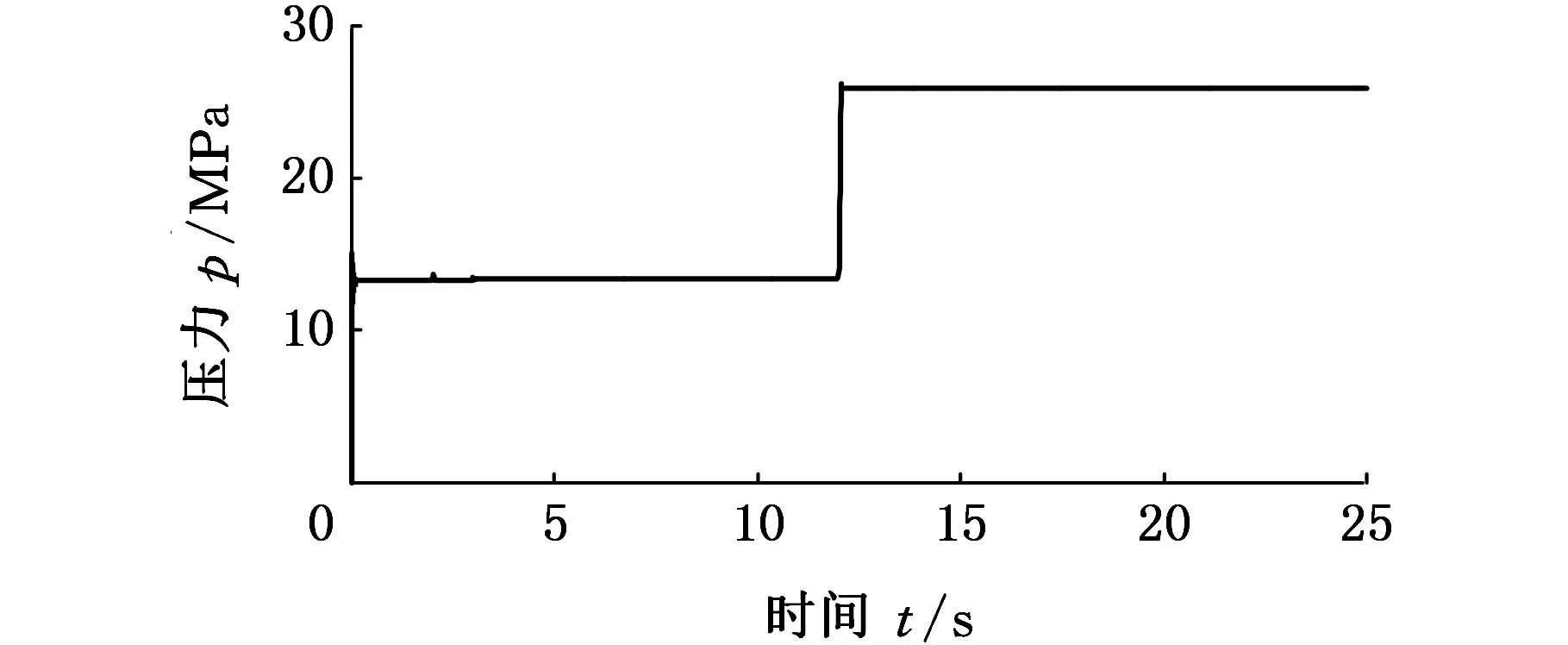
(a)推进油缸负载突变

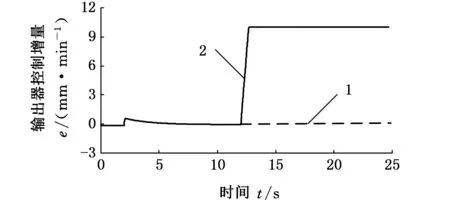
(b)控制器输出增量 1.有推进油缸压力信号 2.无推进油缸压力信号图6 压力突变时控制器输出增量Fig.6 When the pressure changes the controller output incremental

图6a所示为推进油缸的负载压力突变，图6b中,实线表示控制器在调节推进油缸速度时，没有将推进油缸压力信号作为推进速度调节的输入，推进速度控制器输出的误差增量比推进压力正常时增大100倍，这样会导致推进速度调节出现较大的误差，调节过程波动频繁。将推进油缸压力作为推进油缸速度调节过程中的一个参考量时，当推进压力单位时间内平均值达到设定值上限时，控制器输出的调节增量为零，如图6b中虚线所示，同时保持压力突变前的速度。将推进油缸压力信号作为控制器推进速度调节的输入时，当刀盘负载突然增大时，经RBF-PID控制调节，推进速度趋于稳定，避免了过度调节。

如图7所示，RBF神经网络PID控制对全断面掘进机推进液压系统的非线性系统具有较好的控制效果，对负载发生波动也能快速响应[11]。

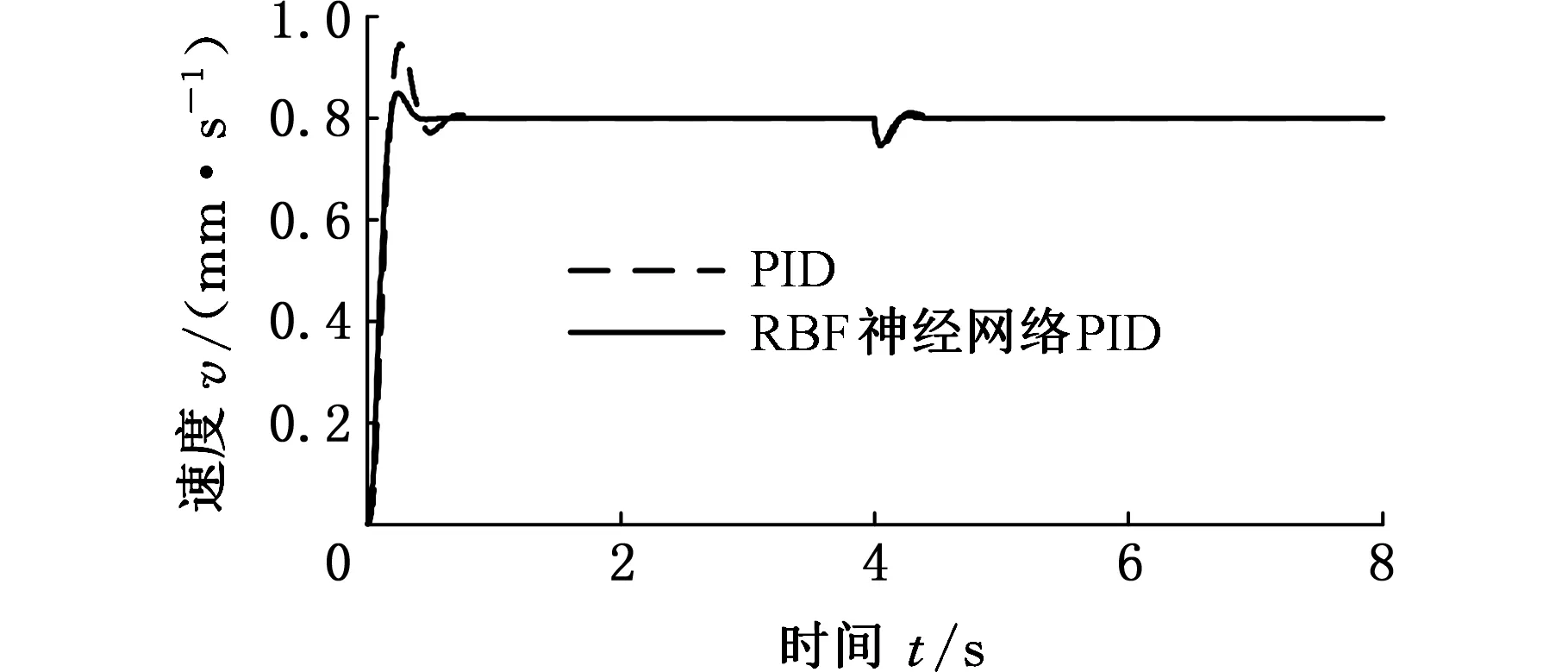
图7 常规PID和RBF神经网络PID对比Fig.7 Comparison of conventional PID and RBF neural networks

5 MTALAB与AMESim联合仿真

TBM推进系统工作模型可分为液压系统模型和控制系统模型两部分, 其中液压模型在 AMESim环境下构造, 控制模型部分则在 MATLAB Simulink中完成[12]。

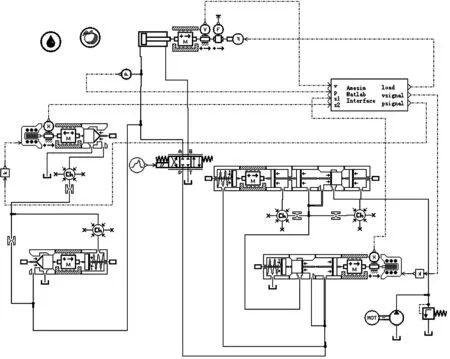
图8 MATLAB与AMESim联合仿真模型Fig.8 MATLAB and AMESim joint simulation model

在AMESim中将调速阀和调压阀设定值作为MATLAB的输出，将推进油缸压力和速度、调速阀和调压阀的位移作为输出[13]。如图9所示，仿真时将调速阀速度设定为0.8 mm/s，控制推进油缸的电磁换向阀在0.6 s时打开，仿真开始3 s后，推进油缸的负载由160 kN变为100 kN，如图9a所示。联合仿真开始0.6 s后，打开控制推进油缸的电磁换向阀，推进速度在0.1 s内达到设定值；仿真开始3 s后，推进油缸负载突变，推进油缸的推进速度在0.2 s内达到稳定。

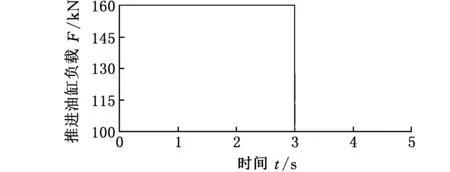
(a)推进油缸负载突变

(b)推进油缸推进速度响应图9 联合仿真负载扰动推进速度响应Fig.9 Joint simulation load disturbance propulsion speed response

6 试验验证

将KSZ-2600型全断面快速硬岩掘进作为试验平台，其刀盘直径为3.6 m，长25 m。通过西门子S7300型PLC采集推进压力、速度和转速，经过上位机控制器程序对推进控制进行分析处理，然后让PLC调节推进油缸的调压阀和调速阀，并在上位机界面显示控制参数。

在北京房山硬岩隧道内进行推进控制试验。采集设备正常运行时70 min的推进压力和推进速度。如图10、图11所示，推进压力在10～13 MPa内变化，推进速度为25～40 mm/min。试验证明，本文基于RBF神经网络的PID推进压力和推进速度联合控制方法能够有效调节推进压力和推进速度，并保持推进速度和推进压力小范围波动[14]，对外部负载突变有很好的抑制能力，提高了掘进效率。

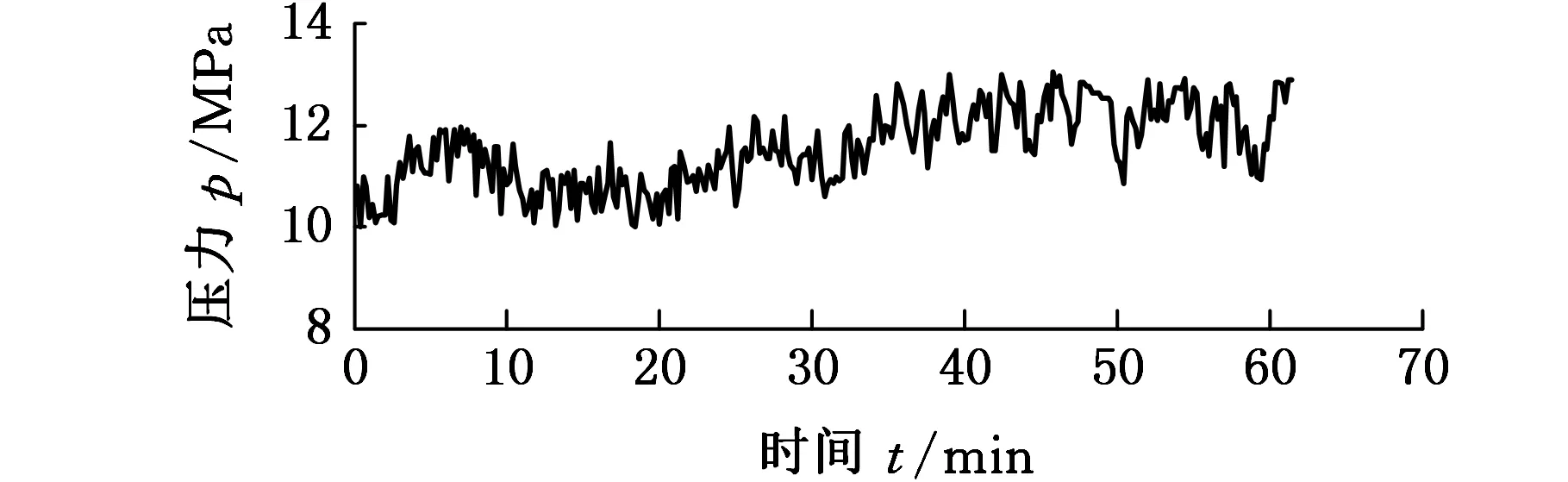
图10 推进压力试验数据Fig.10 Propulsion pressure of experimental data

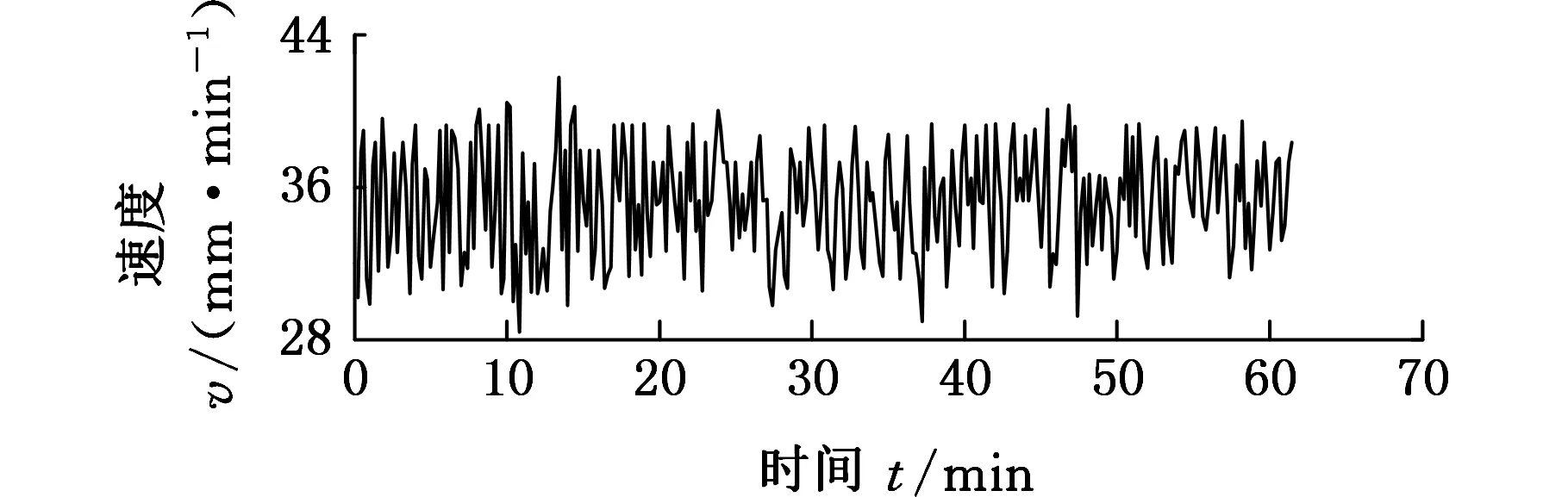
图11 推进速度试验数据Fig.11 Propulsion speed of experimental data

7 结语

本文建立了推进系统的数学模型，设计了RBF神经网络PID控制器及其他两个PID闭环控制器，优化了推进压力和推进速度耦合关系。利用MATLAB与AMESIM联合仿真验证了所建数学模型的准确性。在负载发生较大波动的情况下，控制系统能够快速响应并达到稳定；同时也验证了推进压力作为推进速度控制器的输入能够有效地减小推进速度的输出误差。最后通过全断面掘进机试验验证了基于RBF神经网络PID的推进压力和推进速度联合匹配控制，可克服地质条件复杂时较大的负载扰动，提高掘进效率。

[1] 周奇才, 黄克, 赵炯, 等. 基于改进型滑动窗主元分析的盾构液压系统故障诊断研究[J]. 中国机械工程, 2013, 24(5):638-643. ZHOU Qicai, HUANG Ke, ZHAO Jiong, et al. Study on Fault Diagnosis of Shield Hydraulic System Based on Improved Sliding Window Principal Component Analysis[J]. China Mechanical Engineering, 2013, 24 (5): 638-643.

[2] 胡国良, 龚国芳, 杨华勇. 盾构掘进机土压平[J]. 浙江大学学报(工学版), 2006, 40(5): 874- 877. HU Guoliang, GONG Guofang, YANG Huayong. Earth Press of Shield Tunneling Machine[J]. Journal of Zhejiang University (Engineering Science), 2006, 40 (5): 874-877.

[3] 施虎, 龚国芳, 杨华勇,等. 基于单神经元的盾构推进速度自适应PID控制[J]. 中国机械工程, 2009, 20(2): 138-141. SHI Hu, GONG Guofang, YANG Huayong, et al. Adaptive Speed PID Control of Shield Driving Speed Based on Single Neuron[J]. China Mechanical Engineering, 2009, 20 (2): 138-141.

[4] 杨扬, 龚国芳, 胡国良，等. 基于AMESim和MATLAB的盾构推进液压系统仿真[J].液压与机床, 2006(6): 119-121. YANG Yang, GONG Guofang, HU Guoliang, et al. Shield Thrust Hydraulic System Based on AMESim and MATLAB Simulation[J]. Journal of Hydraulic and Machine Tools, 2006(6):119-121.

[5] 李刚, 朱立达, 杨建宇,等. 基于CSM模型的硬岩TBM滚刀磨损预测方法[J]. 中国机械工程, 2014, 25(1):32-35. LI Gang, ZHU Lida, YANG Jianyu, et al. Prediction Method of TBM Hob Wear in Hard Rock Based on CSM Model[J]. China Mechanical Engineering, 2014, 25 (1):32-35.

[6] 李琳, 张峰榕, 陶建峰,等. 基于断裂力学的TBM撑靴液压缸O形圈断裂分析[J]. 中国机械工程, 2016, 27(12):1563-1567. LI Lin, ZHANG Fengrong, TAO Jianfeng, et al. Fracture Analysis of O Ring of TBM Boot Hydraulic Cylinder Based on Fracture Mechanics[J]. China Mechanical Engineering, 2016, 27 (12):1563-1567.

[7] 张振, 龚国芳,吴伟强. 硬岩隧道掘进机推进系统姿态自适应控制[J]. 浙江大学学报(工学版)，2015,49(10): 1870-1877. ZHANG Zhen, GONG Guofang, WU Weijiang. Hard Rock Tunnel Boring Machine Propulsion System Attitude Adaptive Control[J]. Journal of Zhejiang University (Engineering Science), 2015,49 (10) : 1870-1877.

[8] 张振, 龚国芳,饶云意. TBM试验台支撑推进液压系统设计与仿真分析[J].工程设计, 2015(4): 324-329. ZHANG Zhen, GONG Guofang, RAO Yunyi. The Design and Simulation Analysis of Hydraulic System for TBM Testing Platform[J]. Engineering Design, 2015(4): 324-329.

[9] 苏健行. 全断面掘进机综合试验台液压系统及调速特性研究[D].杭州：浙江大学, 2008. SU Jianxing. Comprehensive Test Bed Hydraulic System and Speed Regulating Characteristics of the Whole Section[D]. Hangzhou：Zhejiang University, 2008.

[10] YANG Huayong, SHI Hu. Electro-hydraulic Proportional Control of Thrust System for Shield Tunneling Machine[J]. Automation in Construction, 2009,18:950-956.

[11] 李苏铭.数字控制电液比例插装流量阀非线性校正方法研究[D].太原：太原理工大学, 2015：23-32. LI Suming. Study on Nonlinear Correction Method of Digital Controlled Electro-hydraulic Proportional Plug Flow Valve [D]. Taiyuan: Taiyuan University of Technology, 2015：23-32.

[12] 刘益民. 基于改进BP神经网络的PID控制方法的研究[J]. 浙江大学学报 (工学版) , 2006, 40(5): 874- 877. LIU Yimin. Research on PID Control Method Based on Improved BP Neural Network[J]. Journal of Zhejiang University (Engineering Science), 2006, 40 (5): 874-877.

[13] 刘益民. 基于改进BP神经网络的PID控制方法的研究[D]. 西安：中国科学院研究生院西安光学精密机械研究所，2007. LIU Yimin. Research on PID Control Method Based on Improved BP Neural Network[D]. Xi’an：Graduate University of Chinese Academy of Sciences (Institute of Optics and Precision Mechanics) 2007.

[14] FEI L, WANG J, ZHANG L, et al. Fractional-Order PID Control of Hydraulic Thrust System for Tunneling Boring Machine[C]// International Conference on Intelligent Robotics and Applications. Busan, Korea, 2013:470-480.

(编辑 张 洋)

Adaptive PID Control Based on RBF Neural Network for TBMs

SONG Liye WAN Yingcai

Academy of Electrical and Control Engineering,Liaoning Technical University,Huludao,Liaoning,125105

The matching problems for full cross section TBM thrust pressures and thrust speeds, the applications of RBF neural network algorithm were designed to make the thrust pressures and the thrust speeds matching and speed adaptive controller might quickly follow the set goals. The controller was simulated by MATLAB, and the hydraulic control model of propulsion systems was established in AMESim and co-simulation with MATLAB. By joint simulation, the controller might make the cutter driving speeds and thrust pressures follow the set target when the cutter load pressures were abrupt. Experiments show that the controller has a good ability to suppress the load disturbances, and may improve the propulsion speeds obviously and push the pressure coupling degrees and reduce the fluctuation ranges of the both.

full cross section tunnel boring machine(TBM); hydraulic control; adaptive control; large disturbance

2016-09-30

国家自然科学基金资助项目(51304107)；液压传动新技术及装备资助项目(LT2013009)

TH137

10.3969/j.issn.1004-132X.2017.14.007

宋立业，男，1972年生。辽宁工程技术大学电气与控制工程学院副教授、博士研究生。主要研究方向为电力系统自动化、盾构机自动控制。发表论文20余篇。E-mail:372492761@qq.com。万应才，男，1990年生。辽宁工程技术大学电气与控制工程学院硕士研究生。