基于软竞争Yu范数自适应共振理论的轴承故障诊断方法

慕海林 王志刚 徐增丙

自适应共振理论的轴承故障诊断武汉科技大学机械自动化学院，武汉，430081



基于软竞争Yu范数自适应共振理论的轴承故障诊断方法

慕海林 王志刚 徐增丙

自适应共振理论的轴承故障诊断武汉科技大学机械自动化学院，武汉，430081

传统自适应共振理论网络模型利用硬竞争机制对故障类边界处的样本进行分类时易造成误分类，为此，提出了基于软竞争Yu范数自适应共振理论的轴承故障诊断方法。将基于模糊竞争学习的软竞争方法引入Yu范数自适应共振理论模型中，根据模式节点与输入样本间隶属度的大小，对竞争层多个节点进行训练和学习。通过对轴承故障试验数据的诊断分析可知，该方法不但能有效识别不同类型的故障，而且能识别不同严重程度故障，且诊断精度优于自适应共振理论模型和模糊C均值聚类模型。

故障诊断；自适应共振理论；软竞争；Yu范数

0 引言

滚动轴承是机械系统中常用的重要部件，其运行状态直接影响整个系统的性能，一旦发生故障或失效，将引发设备产生灾难性后果，因此，对轴承故障进行诊断具有重要意义。人工神经网络因其非线性映射、鲁棒性强、自组织和自学习能力强等特点，在故障诊断中得到了广泛的应用[1-3]。传统神经网络不能在保存以前学习知识的前提下接纳新的模式，导致其应用范围受到了限制。自适应共振理论(adaptive resonance theory，ART)神经网络模型解决了传统神经网络“适应性”与“稳定性”两难的问题，而广泛应用于模式识别、故障分类等领域。但ART网络采用硬竞争机制，浪费了神经元信息，常将处于故障类边界处的数据点强行误分为另一故障类，导致诊断精度不高。针对这一问题，笔者将软竞争方法[4]引入ART网络模型，提高神经元节点信息的利用率，从而提高诊断模型的诊断效果。

1 ART神经网络

ART神经网络[5]利用生物神经细胞之间自兴奋与侧抑制的动力学原理，让输入模式通过网络的双向连接进行识别与比较，通过达到共振状态完成网络的训练与学习，解决了传统神经网络“适应性”与“稳定性”两难的问题，其基本结构如图1所示。网络分为比较层F1和识别层F2，当一个输入模式提交给网络的F1层时，在F2层比较各节点与输入模式的相似度；硬竞争机制下，F2层每次只有一个节点被激活，并在F1层对应一个反馈信号，反馈信号在F1层与输入模式进行比较。如果输入模式与反馈信号不能匹配，调整子系统将重置F2层，并取消当前胜出的神经元和相对应的反馈信号，从而产生新一轮的竞争。F2层新胜出的神经元通过反馈连接向F1层产生一个新的反馈信号，并在F1层再次进行比较，如此反复地调整、重置，最终达到谐振状态，整个神经网络在谐振状态下不断学习和调整，直到反馈值与输入模式成功匹配完成学习[6]。

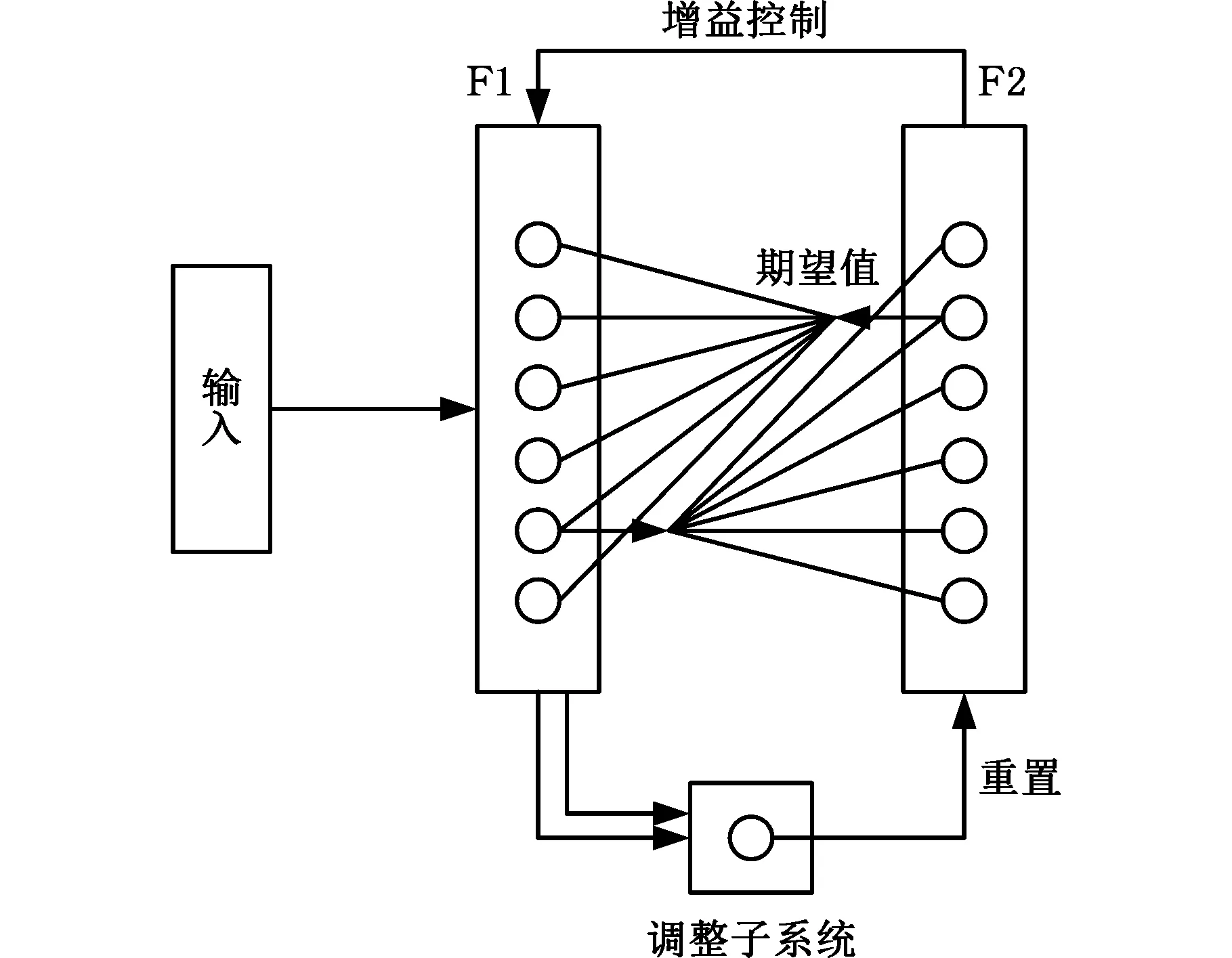
图1 ART网络基本结构Fig.1 Basic structure of ART

2 基于软竞争的Yu范数ART神经网络

2.1 基于Yu范数的ART神经网络

Yu范数[7]由T范数和S范数组成，其数学表达式为

T(x，y)=max(0，(1+τ)(x+y-1)-τxy)

(1)

S(x，y)=min(1，x+y+τxy)

(2)

x，y∈[0，1]τ>-1

根据Yu范数的特有性质，LUUKKA[8]提出等价关系式：

(3)

并将其作为相似测度对样本进行分类，运用在疾病诊断中，该方法得到了较好的分类效果，但需事先确定类别的个数。ART神经网络虽然解决了“适应性”与“稳定性”两难的问题，但其分类性能受训练样本输入顺序的影响。为此，有学者将ART神经网络与等价关系式(式(3))相结合，提出基于Yu范数的ART神经网络模型[9]：

(1)模式选择。假设有N个模式节点，第i类模式节点的权重向量Vi=(Vi(1)，Vi(2)，…，Vi(D))，则输入样本矢量与该模式节点的相似度为

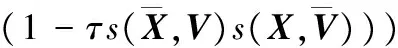
(4)

s(X,V)=min(1,f(X+V+τX×V))

(5)

式中，X、V为D维向量，X、V内的元素均为0、1之间的数；I为D维向量，向量内的元素均为1；f(Z) 表示取向量Z中各元素的平均值。

然后通过

s(X，VJ)>s(X，Vj)

J，j=1，2，…，N且j≠J

式中，VJ为获胜模式节点的权重向量。

得到相似度最大的模式节点，即获胜模式节点。

(2)模式匹配。根据式(4)可以得到获胜节点J与输入样本向量之间的相似度s(X，VJ)，然后将其与警戒参数ρ进行比较。如果s(X，VJ)>ρ，即模式发生匹配，则表示该输入样本矢量被分类于该模式节点所代表的类；否则就重新建立一个新的模式节点，转入步骤(4)。

(3)权重调整。当获胜的模式节点与输入样本向量之间的相似度大于警戒参数ρ时，网络的模式节点的权重向量调整为

VJ=(nVJ0+X)/(n+1)

(6)

式中，VJ0为原始的模式节点的权值矢量；VJ为学习过后的权值矢量；n为属于模式节点J所代表的类的样本个数。

(4)建立新模式节点。如果输入样本A与模式节点J的相似度小于警戒参数ρ，即s(X，VJ)<ρ，则需重新建立一个新的模式节点，其权值向量为

Vn+1=A

(7)

2.2 引入软竞争的Yu范数ART神经网络

Yu范数ART神经网络采用胜者为王的硬竞争机制对模式节点进行分类选择，获胜节点独一无二。但在实际情况中，可能存在多个满足获胜条件的节点，采用硬竞争机制，易造成故障类边界处的数据样本被误分类，降低了分类精度。为此，本文将具有灵活调整软竞争程度和抑制噪声优点的模糊竞争学习(fuzzy competitive learning，FCL)软竞争方法引入Yu范数ART神经网络模型，提出了基于FCL软竞争的Yu范数ART神经网络方法。

在神经网络的竞争层中使用软竞争机制，每次竞争产生多个获胜节点并参与到网络的调整中，使得竞争层中的节点尽可能多地发挥作用，提高竞争层中节点的利用率，减少神经元信息的浪费，从而降低故障类边界处数据样本被误分的概率，提高分类精度。

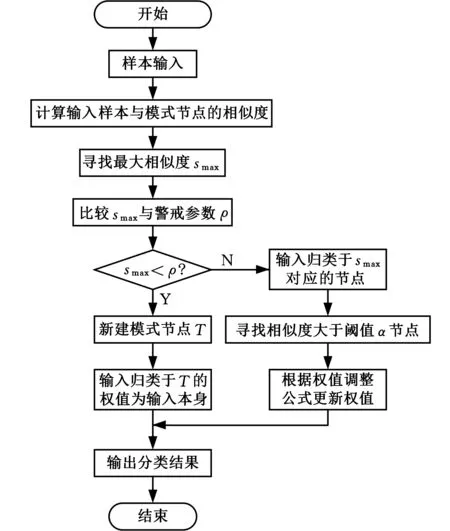
图2 软竞争Yu范数ART神经网络算法流程图Fig.2 Flow chart of Yu’s norm ART based on soft competition

网络模型的算法如图2所示。当输入样本与模式节点的相似度大于设定阈值α时，节点均为获胜节点，并依据节点与输入样本间隶属度的大小调整权值向量。与硬竞争Yu范数ART神经网络模型的算法类似，计算输入样本与各个模式节点的相似度，其中,最大相似度smax所对应节点为获胜节点，将smax与警戒参数ρ进行比较，如果smax<ρ，则新建模式节点；否则输入样本被分类为最大相似度对应节点所代表的类，并采用软竞争机制，即寻找所有相似度大于阈值α的节点，对其进行权重调整，完成网络的学习。

权重调整为

VJ=(nVJ0+hmX)/(n+hm)

(8)

(9)

式中，h为模式节点与输入向量之间的隶属度；c为模式节点总数；x为输入向量；vj为当前模式节点对应的权值向量。

模糊指数m可调整软竞争程度，m→1时，h取值为0或1，软竞争机制退化为硬竞争机制；m→∞时，h取值为1/c，此时隶属度最为模糊。较大的m能够抑制噪声，使隶属度低的噪声点对网络整体的贡献较小。

3 案例分析

3.1 数据获取

数据为美国凯斯西储大学电气工程实验室的滚动轴承数据[10]。选取负载746 W下损伤尺寸为0.1778mm(0.007英寸)的内圈、外圈以及滚动体故障，损伤尺寸为0.5334 mm(0.021英寸)的内圈、外圈故障以及正常状态的6组数据，每种故障状态抽取100组样本，每组样本有4096个采样数据。

3.2 特征提取

对获取的振动信号运用haar小波分析方法进行了4层分解，并分别从每层小波信号中提取了表征信号脉冲现象的峰值因子、裕度指标，以及表征信号能量变化的均方值、能量熵[11]用于刻画轴承故障状态。

3.3 特征优化

考虑到特征参数间的冗余性及相关性对诊断精度的影响，为提高诊断效果，对特征参数进行了优选。基于“类间距离大，类内距离小”的原则[12]，利用相似度(式(4))构建了一种特征参数优选方法[13]，具体算法如下：

(1)提取所有的特征参数，全部特征参数描述如下：

{Sn,f,p|n=1,2,…,100;f=1,2,…,6;

p=1,2,…,20}

(10)

式中，Sn，f，p为f故障下第n个样本的第p个特征参数的值。

(2)对于任意一个特征参数p，首先计算该参数在各个模式下的类内距离

(11)

ni,nj=1,2,…,100且ni≠nj

式中，s(Sni,f,p,Snj,f,p)为特征参数Sni,f,p与Snj,f,p之间的相似度。

然后计算6种故障下的平均类内距离

(12)

(3)计算同一故障下，特征参数p的平均值，即类内中心

(13)

然后计算类与类两两之间的距离的平均值，即类间平均距离

(14)

fi,fj=1,2,…,6且fi≠fj

式中，s(gfi,p,gfj,p)为类内中心gfi,p与gfj,p之间的相似度。

(4)计算类间平均相似度与类内平均相似度的比值

(15)

(5)获取各特征参数的敏感系数

λp=ep/Ep

(16)

式中，Ep为ep的最大值。

依据该算法可分别得到每个特征参数的敏感系数，系数越大说明该参数的分类灵敏度越高。在此实验中，依据经验设置评价系数β，敏感系数大于β的特征即为敏感特征。图3给出了20个特征参数优化选取的结果。

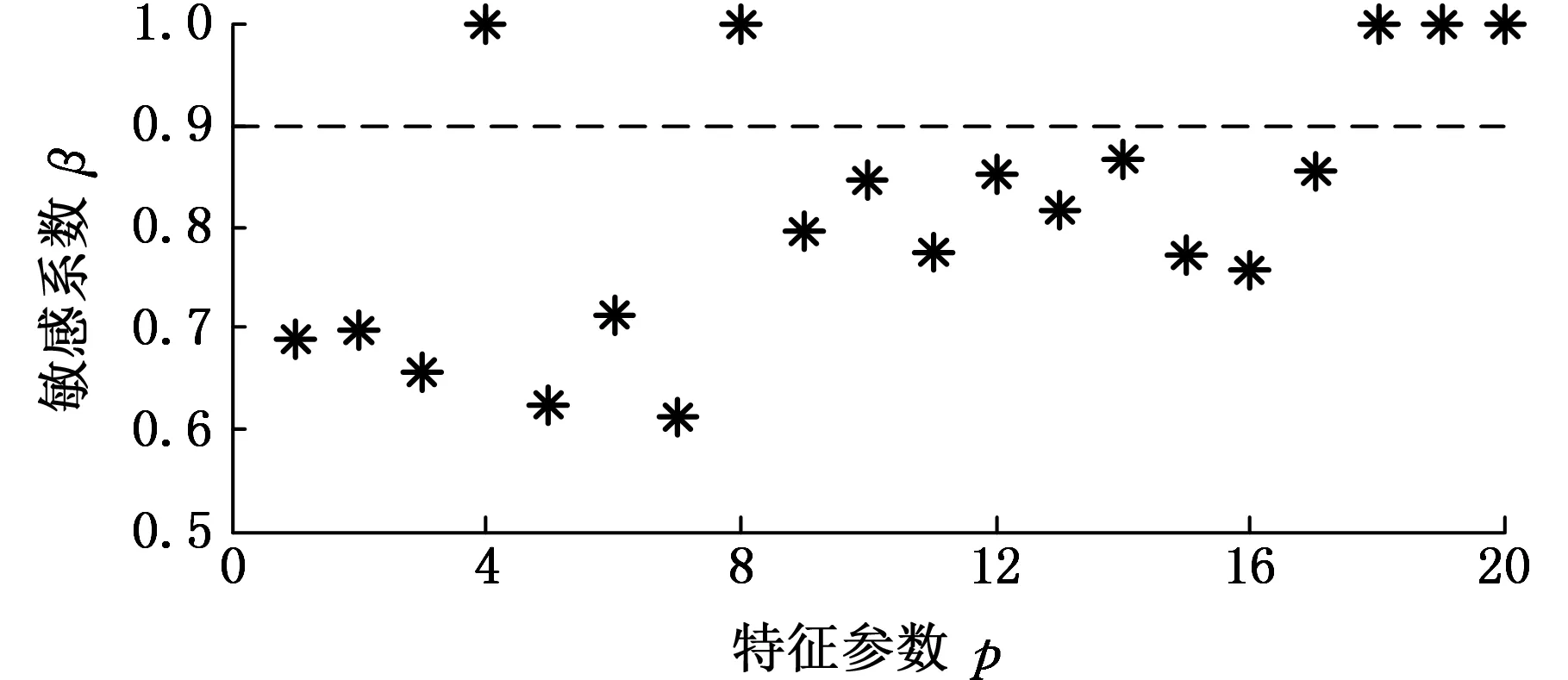
图3 各个特征参数的敏感系数Fig.3 Sensitivity coefficients of characteristic parameters

3.4 诊断分析

该模型的特点在于分类与网络训练同时进行。将敏感特征参数作为故障诊断模型的输入，当第一组样本输入空白网络模型时，该样本构建了第一个模式节点，节点权重为样本本身。当第二组样本输入模型时，计算第二组输入样本与第一个模式节点的相似度并将其与警戒参数比较，若相似度大于警戒参数，则将第二组输入归类于第一个模式节点，并更新权重向量；否则依据该样本新建第二个模式节点。当第三组样本输入时，计算输入与所有节点的相似度并将最大相似度与警戒参数比较，若相似度大于警戒参数，则输入归类于最大相似度所对应的模式节点，且所有相似度大于阈值α的节点均为获胜节点，计算获胜节点与输入间的隶属度，根据各自隶属度的大小更新权重向量；若小于警戒参数，则新建第三个模式节点，在分类的同时完成网络训练，其余样本分类过程以此类推。在诊断过程中，根据由小到大的顺序设置阈值β，进行特征参数的选择，选择的终止条件为诊断精度达到最高，此时阈值β=0.9。模型中参数的确定是在不改变其他参数的情况下，不断增加目标参数值，当诊断精度达到最高时就可得到对应参数值，经分析,模型的警戒参数ρ为0.835，τ为0.4，m为6，阈值α为0.4。诊断结果如图4所示。诊断精度为

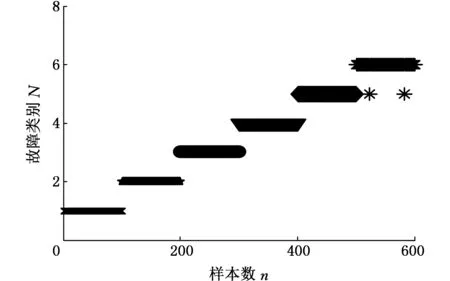
图4 基于软竞争Yu范数ART神经网络分类结果Fig.4 Fig.4 Classification result of Yu’s norm ART based on soft competition

(17)

式中，C为正确分类样本个数；T为样本总数；N为聚类节点数[14]。

如图4所示，样本总数为600，正确分类样本个数为598，由于本文模型的分类与网络训练同时进行，因此聚类节点数为0。计算可得D=99.67%。由图4和诊断精度可以看出，基于软竞争的Yu范数ART模型不仅能有效识别不同类型的故障，而且能识别不同严重程度故障。

3.5 参数分析

图5～图8给出了各个参数取不同值时的诊断结果，可以看出，随着参数ρ、τ的增大，模型的分类精度不断提高，但当达到模型的极限时，分类精度反而降为0；参数α的改变对模型分类精度影响较小，在取值较大时，分类精度略微降低；参数m趋于1时，模型退化为硬竞争机制，分类精度较低，随着m的增大，软竞争程度不断提高，模型的分类精度也不断提高。因此，参数值只有在合适的区间内取值时，才能得到最高的分类精度。

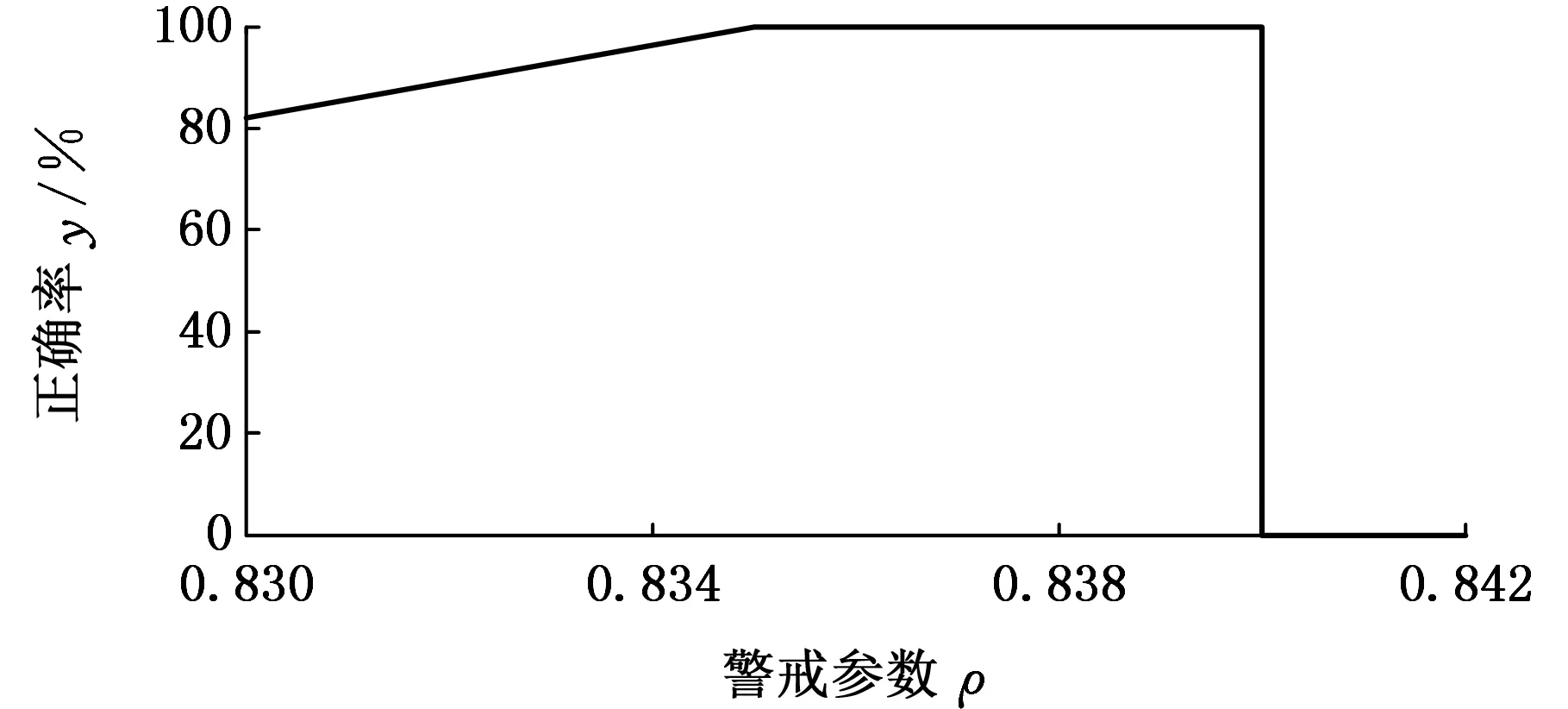
图5 改变模型参数ρ的分类结果Fig.6 Classification result with the change of ρ

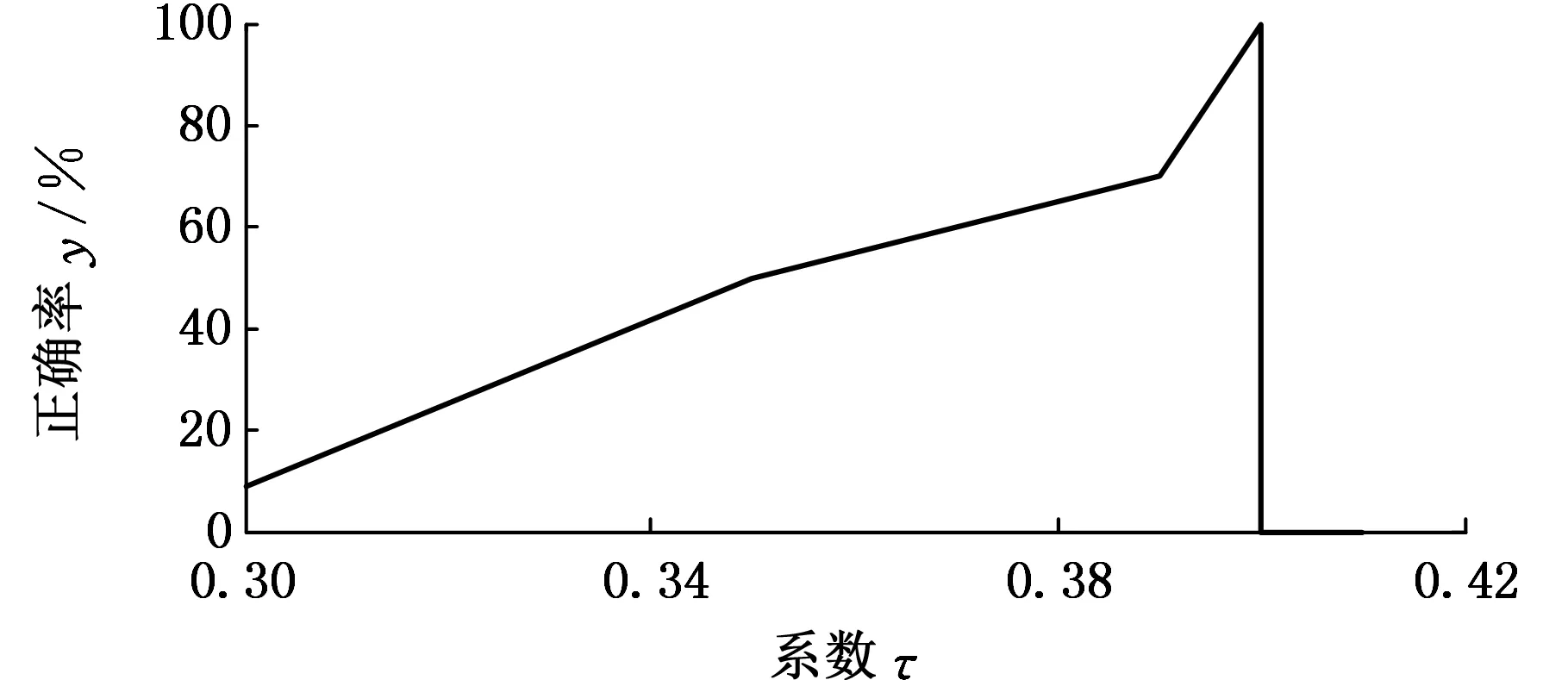
图6 改变模型参数τ的分类结果Fig.6 Classification result with the change of τ

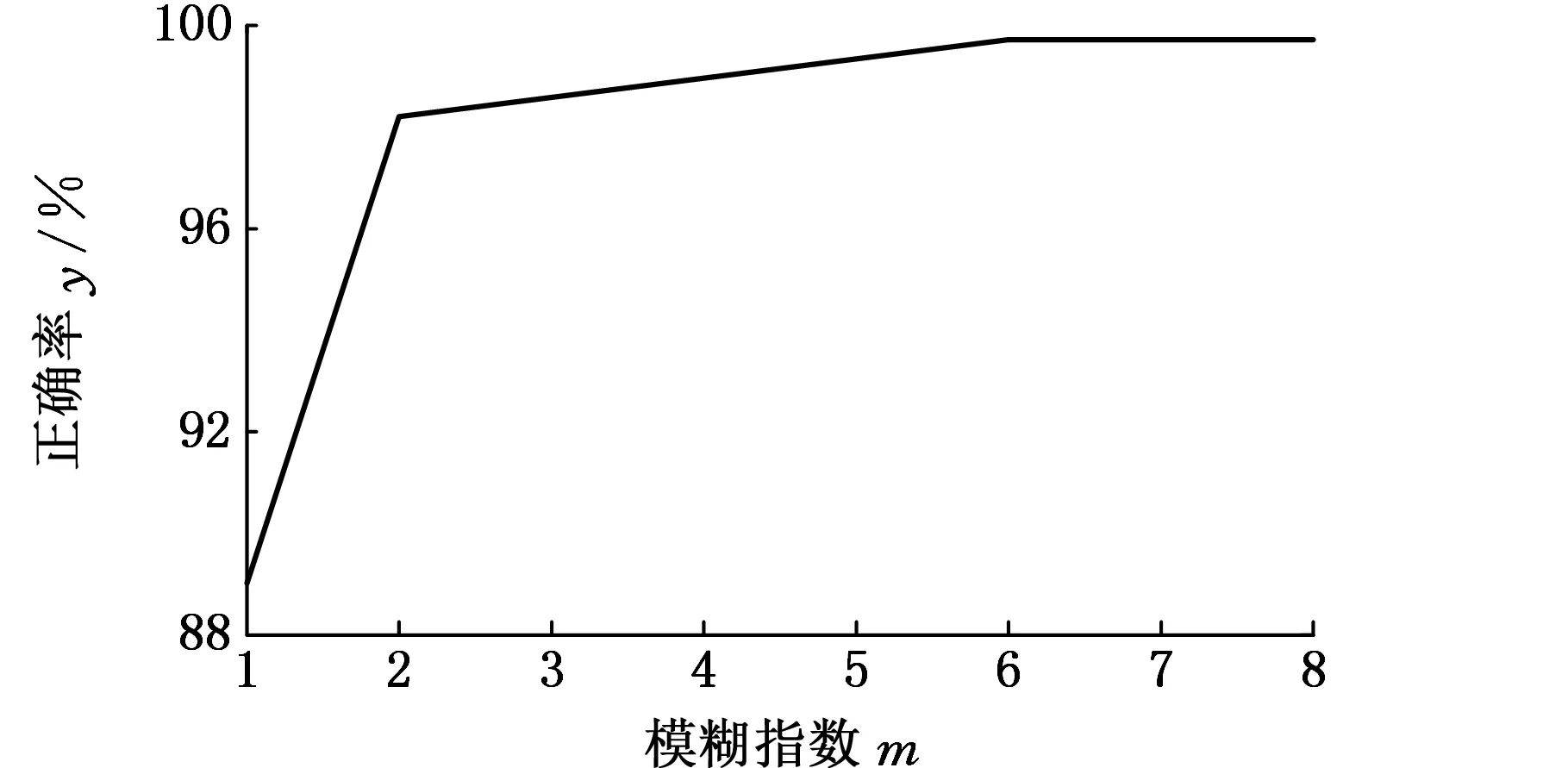
图7 改变模型参数m的分类结果Fig.7 Classification result with the change of m

3.6 性能比较分析

为了验证本文诊断模型的优越性，将原ART神经网络模型、Yu范数ART模型和模糊C均值聚类模型对同样的数据样本进行了诊断分析，其分类结果如表1所示。由表1可以看出，模糊C均值[15]聚类的诊断精度最低，软竞争Yu范数ART模型分类精度高达99.67%，且比硬竞争ART模型和Yu范数ART模型的分类精度分别高了16.34%和10.5%。

表1 模型分类结果Tab.1 Classification results of models %

4 结论

(1)软竞争机制可以更加准确地诊断模糊区域处的数据样本，使得基于软竞争Yu范数ART的故障诊断方法具有更高的诊断精度。

(2)软竞争Yu范数ART模型不仅能有效识别不同类型的故障，而且能识别不同严重程度故障，表明其对早期故障的诊断有着一定的效果，可以进一步探究该模型在早期故障诊断中的应用。

[1] 郑近德，程军圣，杨宇.多尺度排列熵及其在滚动轴承故障诊断中的应用[J].中国机械工程，2013，24(19) ：2641-2647. ZHENG Jinde，CHENG Junsheng，YANG Yu.Multi-scale Permutation Entropy and Its Applications to Rolling Bearing Fault Diagnosis[J]. China Mechanical Engineering，2013，24(19) ：2641-2647.

[2] 裴峻峰，毕昆磊，吕苗荣，等.基于多特征参数和概率神经网络的滚动轴承故障诊断方法[J].中国机械工程，2014，25(15)：2055-2058. PEI Junfeng，BI Kunlei，LYU Miaorong，et al.Fault Diagnosis of Roller Bearings Based on Characteristic Parameters and Probabilistic Neural Network[J]. China Mechanical Engineering，2014，25(15)：2055-2058.

[3] 李胜，张培林，李兵，等.量子BP神经网络在发动机故障诊断中的应用[J].中国机械工程，2014，25(16)：2159-2163. LI Sheng，ZHANG Peilin，LI Bing，et al. Applications of Quantum BP Neural Network in Engine Fault Diagnosis[J]. China Mechanical Engineering，2014，25(16)：2159-2163.

[4] JOU C C.Fuzzy Clustering Using Fuzzy Competitive Learning Networks[C]//International Joint Conference on Neural Networks.Miami：IEEE，1992：714-719.

[5] CARPENTER G A，GROSSBERG S.A Massively Parallel Architecture for a Self-organizing Neural Pattern Recognition Machine[J]. Computer Vision, Graphics, and Image Processing, 1987, 37:54-115.

[6] 高晓红.ART神经网络的发展与应用[J].电脑知识与技术(学术交流)，2007，20：509-526. GAO Xiaohong. Development and Application of ART Neural Networks[J]. Computer Knowledge and Technology(Academic Exchange) ，2007，20：509-526.

[7] YU Yandong. Triangular Norms and TNF-sigma-algebras[J]. Fuzzy Sets and Systems，1985，16(3)：251-264.

[8] LUUKKA P. Similarity Classifier Using Similarity Measure Derived from Yu’s Norms in Classification of Medical Data Sets[J]. Computers in Biology and Medicine，2007，37(8)：1133-1140.

[9] 徐增丙，李友荣，王志刚，等. 基于ART和Yu范数的聚类方法在齿轮故障诊断中的应用[J].武汉科技大学学报，2016，39(2)：116-120. XU Zengbing，LI Yourong，WANG Zhigang，et al.A Novel Clustering Method Combining ART with Yu’s Norm for Fault Diagnosis of Bearings [J].Journal of Wuhan University of Science and Technology，2016，39(2)：116-120.

[10] The Case Western Reserve University Bearing Data Center. Bearing Data Center Fault Test Data[EB/OL]. (1998-10-04).http://csegroups.case.edu/bearingdatacenter/pages/download-data-file.

[11] 王洪明，郝旺身，韩捷，等.全矢LMD能量熵在齿轮故障特征提取中的应用[J].中国机械工程，2015，26(16)：2160-2164. WANG Hongming，HAO Wangshen，HAN Jie，et al.Full Vector LMD Energy Entropy in Gear Fault Feature Extraction[J]. China Mechanical Engineering，2015，26(16)：2160-2164.

[12] 于耀亮，姜嘉言，张立明.一种新的距离测度学习算法[J].信息与电子工程，2008(2)：115-119. YU Yaoliang，JIANG Jiayan，ZHANG Liming. ANew Distance Metric Learning Algorithm[J]. Information and Electronic Engineering，2008(2)：115-119.

[13] 张任.基于振动信号的齿轮箱智能故障诊断方法研究[D].北京：北京化工大学，2013. ZHANG Ren.Intelligent Fault Diagnosis Method Research of Gearbox Based on Vibration Signal[D].Beijing：Beijing University of Chemical Technology，2013.

[14] YANG B S，HAN T，AN J L.ART-KOHONEN Neural Network for Fault Diagnosis of Rotating Machinery[J]. Mechanical Systems and Signal Processing，2004，18(3)：645-657.

[15] 王书涛，张金敏，张淑清，等.基于威布尔与模糊C均值的滚动轴承故障识别[J].中国机械工程，2012，23(5) ：595-598. WANG Shutao，ZHANG Jinmin，ZHANG Shuqing，et al. Fault Diagnosis of Rolling Bearings Based on Weibull Distribution and Fuzzy C Means Clustering Analysis[J].China Mechanical Engineering，2012，23(5) ：595-598.

(编辑 张 洋)

ISSN 1004-132X

CHINA MECHANICAL ENGINEERING

(Transactions of CMES)

Vol.28,No.14,2017 the second half of July

Semimonthly(Serial No.470)Edited and Published by:CHINA MECHANICAL

ENGINEERING Magazine Office

Add：P.O.Box 772,Hubei University of Technology, Wuhan,430068,ChinaDistributer Abroad by: China International Book

Trading Corporation (P.O.Box 399,Beijing)

Code:SM4163

Fault Diagnosis Method of Bearings by Yu’s Norm ART Based on Soft Competition

MU Hailin WANG Zhigang XU Zengbing

School of Machinery and Automation,Wuhan University of Science and Technology,Wuhan,430081

Fault interfaces were categorized wrongly by ART with hard competition. A new fault diagnosis method by Yu’s norm ART was proposed based on soft competition. The soft competition method of fuzzy competitive learning(FCL) was introduced into Yu’s norm ART, neural nodes in the competition layer were trained according to the degree of membership among the mode nodes and the inputs. Bearing fault data were used to validate the fault diagnosis model, which proves that the fault diagnosis model may distinguish different faults, and distinguish different fault degrees under the same fault types. Comparing with other methods for fault diagnosis, such as ART and fuzzy C-means clustering, the proposed method has higher diagnostic accuracy.

fault diagnosis; adaptive resonance theory(ART); soft competition; Yu’s norm

2016-09-02

国家自然科学基金资助项目(51405353)

TH17；TP183

10.3969/j.issn.1004-132X.2017.14.018

慕海林，男，1992年生。武汉科技大学机械自动化学院硕士研究生。主要研究方向为故障诊断。E-mail:285916325@qq.com。王志刚，男，1973年生。武汉科技大学机械自动化学院教授、博士研究生导师。徐增丙，男，1981年生。武汉科技大学机械自动化学院副教授。