考虑尺寸的三维胶结颗粒法向接触强度估算公式

刘 芳，周向楠，蒋明镜

(1.同济大学 土木工程防灾国家重点实验室，上海 200092；2.同济大学 土木工程学院 地下建筑与工程系，上海 200092；3.同济大学 岩土及地下工程教育部重点实验室，上海 200092)



考虑尺寸的三维胶结颗粒法向接触强度估算公式

刘 芳1,2,3，周向楠2,3，蒋明镜1,2,3

(1.同济大学 土木工程防灾国家重点实验室，上海 200092；2.同济大学 土木工程学院 地下建筑与工程系，上海 200092；3.同济大学 岩土及地下工程教育部重点实验室，上海 200092)

粒间胶结的存在导致天然结构性土体具有独特的宏观变形和强度特性。为了研究法向加载条件下三维胶结颗粒的接触破坏规律及尺寸效应，采用有限元法模拟了理想球形胶结颗粒的法向接触力学试验，并将有限元与离散元的模拟结果进行了对比，分析了不同直径比和厚宽比情况下胶结颗粒抗拉压强度的变化规律，得到了胶结颗粒法向接触强度与胶结尺寸参数的定量关系。结果表明：胶结物的直径比和厚宽比显著影响胶结颗粒法向抗压强度，厚宽比占主导作用，抗压强度随着厚宽比增加显著降低；但胶结颗粒抗拉强度的尺寸效应不显著。

岩土工程；胶结材料；接触力学；有限元模拟；尺寸效应

粒间胶结广泛存在于天然岩土材料中(如结构性砂土、软岩和土石混合体等)[1]，显著影响颗粒尺度上的粒间力传递方式。由于外部荷载和环境改变，粒间胶结可能发生破损引起颗粒重新排列，从而导致胶结岩土材料具有独特的宏观变形与强度特性[2-4]。合理描述胶结颗粒微观接触力学行为成为发展胶结岩土材料离散元模拟方法的关键[5]，而描述胶结颗粒承载能力的微观胶结破坏准则是其重要组成部分。

目前，已有学者采用微观模型试验研究了胶结颗粒接触强度的影响因素，并在二维试验条件下证实胶结尺寸对胶结接触强度的重要影响[6-13]。为了在更加可控的试验条件下得到胶结接触强度与粒间胶结几何参数的定量关系，刘芳等[14-15]采用有限元或离散元数值试验方法研究了二维理想圆盘胶结颗粒的法向接触行为规律，并且获得二维胶结法向接触强度的定量估算方法。在更加接近真实情况的三维胶结颗粒模拟方面，Z.F.SHEN等[16]采用离散元法研究了三维条件下脆性胶结颗粒在不同复杂加载条件下的力学响应和破坏准则。相对于二维颗粒接触行为研究而言，三维颗粒接触行为的研究仍显不足。

因此，笔者在前期二维胶结颗粒接触数值试验研究基础上[14]，采用有限元方法模拟三维球形胶结颗粒的法向接触力学试验，进一步研究法向压缩和拉伸加载条件下的三维胶结颗粒接触破坏规律及尺寸效应，以期获得三维条件下球形胶结颗粒法向接触抗压和抗拉强度的定量估算方法。

1 有限元模型

笔者采用的胶结颗粒模型如图1。土颗粒近似为理想圆球，直径为Ds，为了便于在有限元模拟中施加荷载，取半球考虑。颗粒间附着胶结物，粒间胶结宽度为Db，粒间胶结最小厚度为Hb，粒间胶结的几何特征通过两个无量纲物理量来描述，即直径比ξ=Ds/Db和胶结厚宽比η=Hb/Db，其中ξ表征胶结物与颗粒接触面的弯曲程度，sinθ=1/ξ，角度θ的定义见图1，取值在0°到90°之间。在本研究中，为了便于与三维离散元模拟结果[16]进行对比，Db取定值6 mm，ξ在2～5范围变化，η在0.2～0.5范围变化。

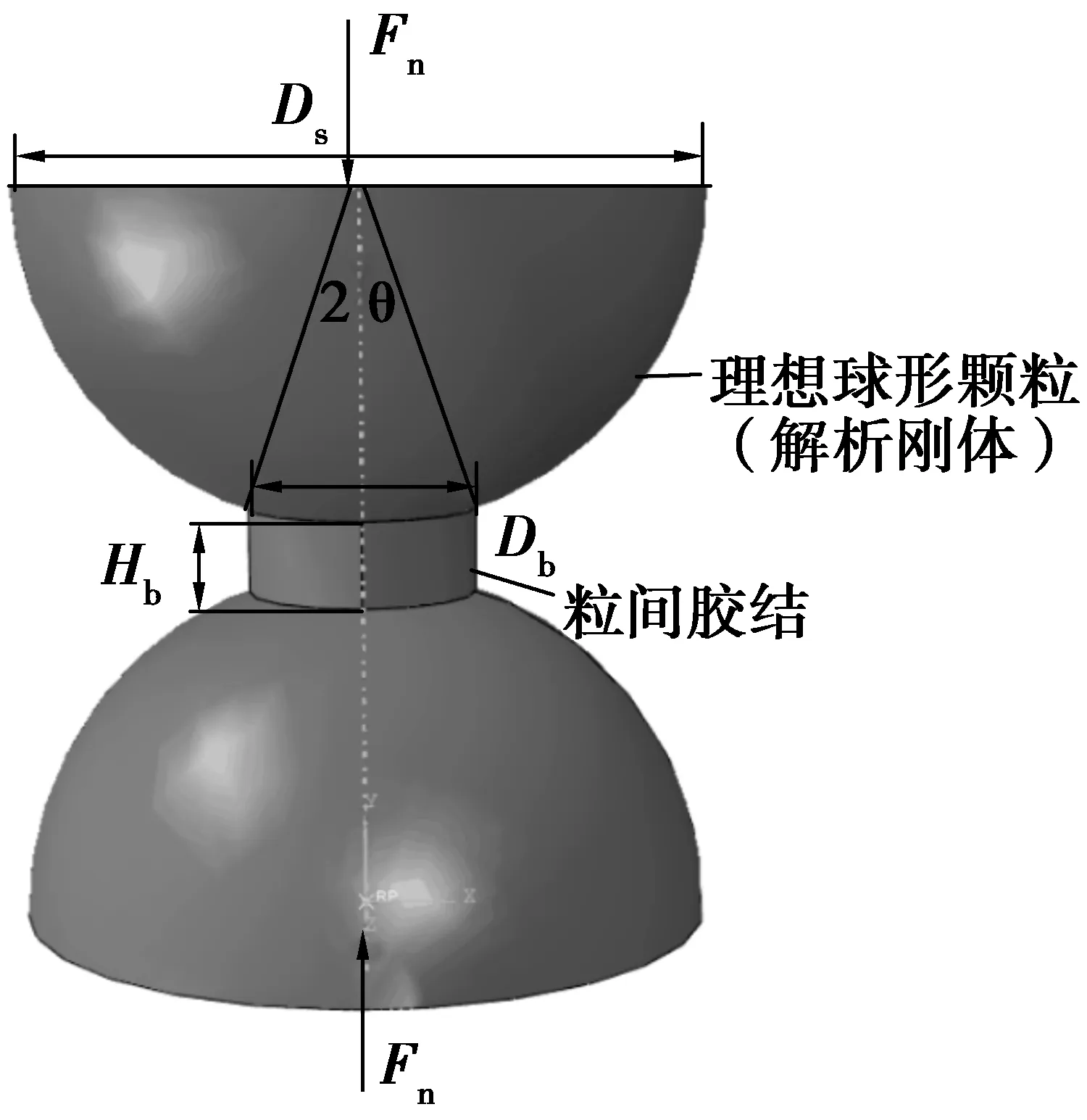
图1 颗粒的模型示意Fig. 1 A schematic illustration of the particle model

笔者采用有限元程序ABAQUS对图1所示的模型进行数值建模。由于土颗粒刚度一般远大于粒间胶结材料刚度，为简化分析，采用解析刚体模拟颗粒，不需要进行单元划分，下部刚体参考点施加固端约束，上部刚体的参考点施加相应的位移和荷载条件。图2为其中一个算例粒间胶结部分的单元网格图(节点数1 325，单元数960)，单元类型为C3D8R。胶结物与颗粒之间的接触设定为绑定约束，即假定接触破坏产生在胶结物内部而不是颗粒和胶结物界面。

图2 粒间胶结物的有限元网格Fig. 2 The finite element mesh of the inter-particle cementation

数值模拟中，通过位移控制进行法向荷载施加，即在上部刚体参考点施加法向的正/负位移模拟颗粒受拉/压载荷方式，直至计算不收敛，从而得到胶结物的峰值拉伸荷载Rnt和峰值压缩荷载Rnc，分别定义为胶结颗粒的抗拉和抗压强度。

2 粒间胶结的材料模型及参数标定

粒间胶结物的材料模型采用ABAQUS程序自带的混凝土塑性损伤模型(即CDP模型)[17]，以模拟土颗粒间的脆性胶结。模型参数根据Z.F.SHEN等的文献中粒间胶结物材料试验的离散元模拟曲线进行标定[16]。参数标定结果汇总见表1。

表1 粒间胶结物的材料模型参数

CDP模型中用户自定义部分的屈服应力-非弹性应变、损伤-非弹性应变的取值由GB 50010—2011《混凝土结构设计规范》的经验公式计算得到。图3为粒间胶结物材料单元试验的有限元模拟结果与离散元模拟结果的对比，有限元计算中所采用的本构模型参数见表1。单轴压缩试验有限元结果与离散元结果吻合较好，单轴拉伸试验中，受本构模型所限，有限元模拟所得到的应力-应变关系呈现更为显著的弹脆性，但峰值拉应力与离散元模拟结果在量级上比较接近。

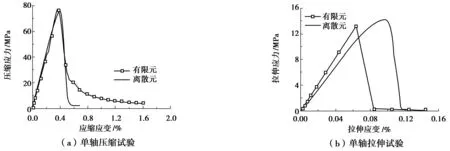
图3 材料参数标定Fig. 3 Material parameters calibration

3 压缩试验的数值模拟结果

3.1 法向荷载响应曲线

图4和图5为不同胶结尺寸下压缩试验数值模拟所得到的法向力与平均应变(即δ/Hb，δ为粒间法向位移)的关系。由图4可见，随着胶结直径比ξ增大，法向力峰值略有增加；当ξ=2时，峰后法向荷载陡然下降到残余值，呈现脆性破坏，当ξ逐渐增加时破坏模式由脆性转为弹塑性破坏；有限元和离散元结果在峰值荷载、峰值荷载位移和破坏模式方面均比较接近。由图5可见，随着胶结厚宽比η的增加，法向力峰值明显降低，有限元和离散元模拟结果基本一致。

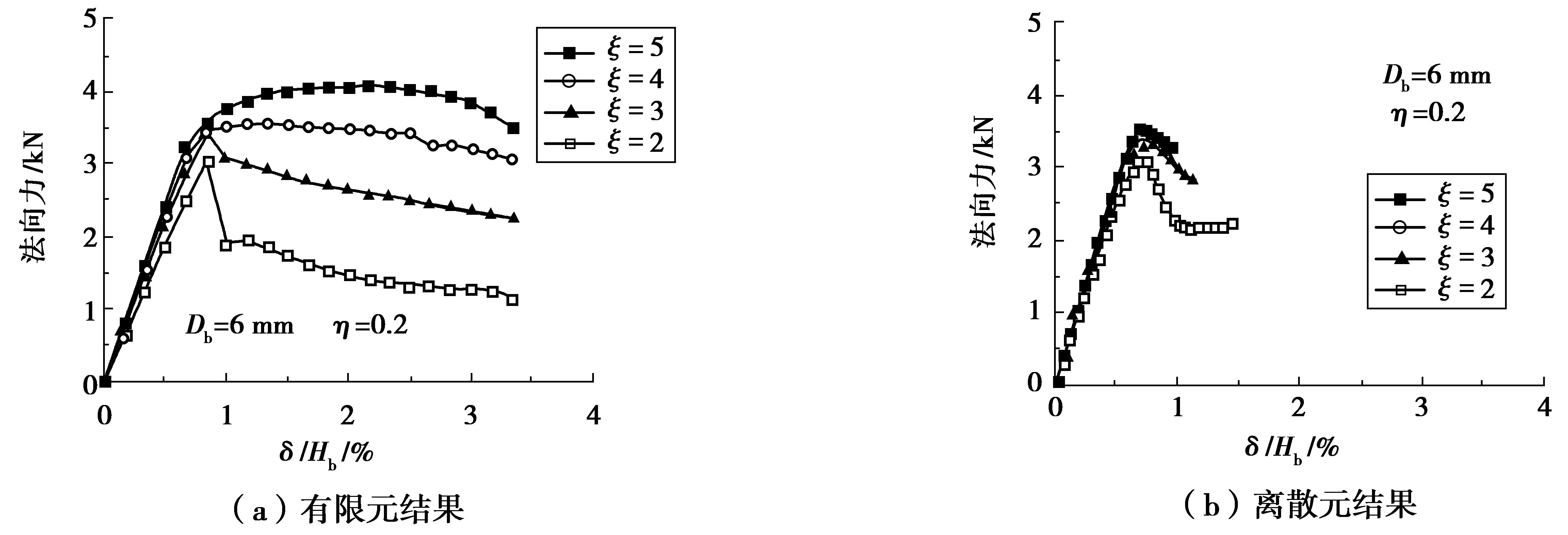
图4 不同胶结直径比下法向压缩荷载与位移关系Fig. 4 Relationship between normal compressive loading and displacement at different diameter ratios of the bond

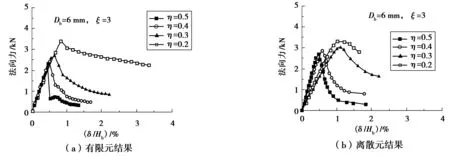
图5 不同厚宽比下的法向压缩荷载与位移关系Fig. 5 Relationship between normal compressive loading and displacement at different thickness-to-width ratios of the bond

3.2 考虑尺寸的法向抗压强度估算公式

胶结颗粒法向抗压强度Rc定义为压缩试验中的峰值荷载，根据数值模拟结果，Rc与粒间胶结尺寸和颗粒大小有关，即具有尺寸效应。

若将Rc进行无量纲化，可根据F.LIU等[15]定义胶结颗粒法向抗压强度因子如下：

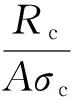
(1)

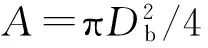
根据式(1)可计算不同尺寸下有限元数值试验所得到的胶结颗粒法向抗压强度因子，绘制其与胶结尺寸参数的关系曲线。图6为χc/(1+sinθ)与胶结厚宽比η的关系曲线。

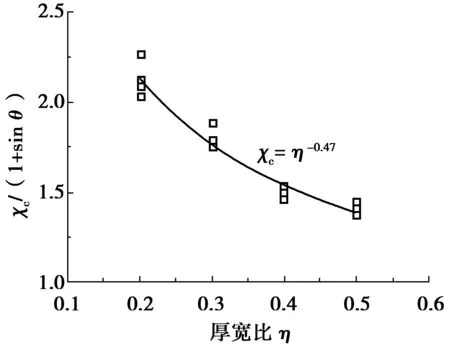
图6 抗压强度因子与粒间胶结厚宽比关系Fig. 6 χc-η relationship obtained in FEM

由图6可见，变量χc/(1+sinθ)与η具有较好归一化关系，可通过幂函数进行拟合，即χc/(1+sinθ)=η-0.47。因此，胶结颗粒法向抗压强度可用式(2)进行估算：

Rc=αηcαθc(Aσc)

(2)

式中：αηc和αθc分别为粒间胶结物的厚宽比系数和界面形状系数，根据本次有限元数值试验的拟合结果，αηc=η-0.47，αθc=1/(1+sinθ)。

图7为粒间胶结物法向应变分别达到1.2εp,2εp和εmax时胶结物轴向垂直截面等效塑性应变的发展情况，其中εp为法向力达到峰值时的应变值，εmax为加载结束时的应变值。

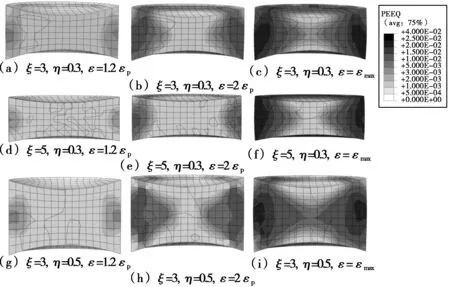
图7 胶结物轴对称面上等效塑性应变发展过程Fig. 7 Development of plastic strain at the axial-symmetric cross-section of the inter-particle cementation

由图7可见，胶结物外边缘首先发生塑性变形，然后向内部扩展，这与试验所观测到的破坏首先以外缘破碎形式发生[13]是一致的。对比图7(a)～(c)和图7(g)～(i)，随着η增加，塑性区更容易贯通，因此胶结颗粒法向抗压强度有所降低；当应变达到εmax时，η=0.5情况下，胶结物塑性区已基本贯通形成剪切带，而η=0.3情况下，受接触面端部约束比较明显，胶结物塑性区仍未贯通。对比图7(a)～(c)和图7(d)～(f)，随着ξ增加，塑性区扩展速度减缓，表明颗粒与胶结物接触界面越接近平面，接触面端部约束越明显，越有利于提高胶结颗粒法向抗压强度。

图8为加载过程中胶结物水平中心截面法向应力的变化情况，胶结中心点为横坐标原点。由图8可见，当法向荷载达到峰值之前，截面各点法向应力均有所增加，中心处应力值高于边缘处；随后，边缘处产生塑性变形破坏，边缘处应力陡然跌落，而中心处仍然处于弹性区，应力骤然上升。对于η=0.5的情况〔见图8(c)〕，当应变达到εmax时，胶结物塑性区已基本贯通，中心处也产生塑性变形破坏，截面各点均发生应力降低；而η=0.3的情况〔见图8(a)和(b)〕，中心处塑性区未贯通，中心处仍有较大应力值。

4 拉伸试验的数值模拟结果

4.1 法向荷载响应曲线

图9和图10为不同胶结尺寸下拉伸试验数值模拟所得到的法向拉伸荷载与平均拉伸应变(即δ/Hb)的关系。由图9，图10可见，区别于压缩试验，粒间胶结在拉伸情况下发生脆性破坏；与压缩试验类似，拉伸荷载峰值随着胶结直径比ξ增大和胶结厚宽比η减小而增加，但是尺寸影响不如压缩试验显著。有限元和离散元结果在峰值荷载、峰值荷载位移和破坏模式方面均比较接近。

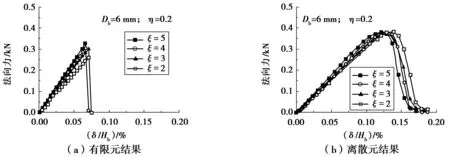
图9 不同胶结直径比下法向拉伸荷载与位移关系Fig. 9 Relationship between normal tensile loading and displacement at different diameter ratios of the bond

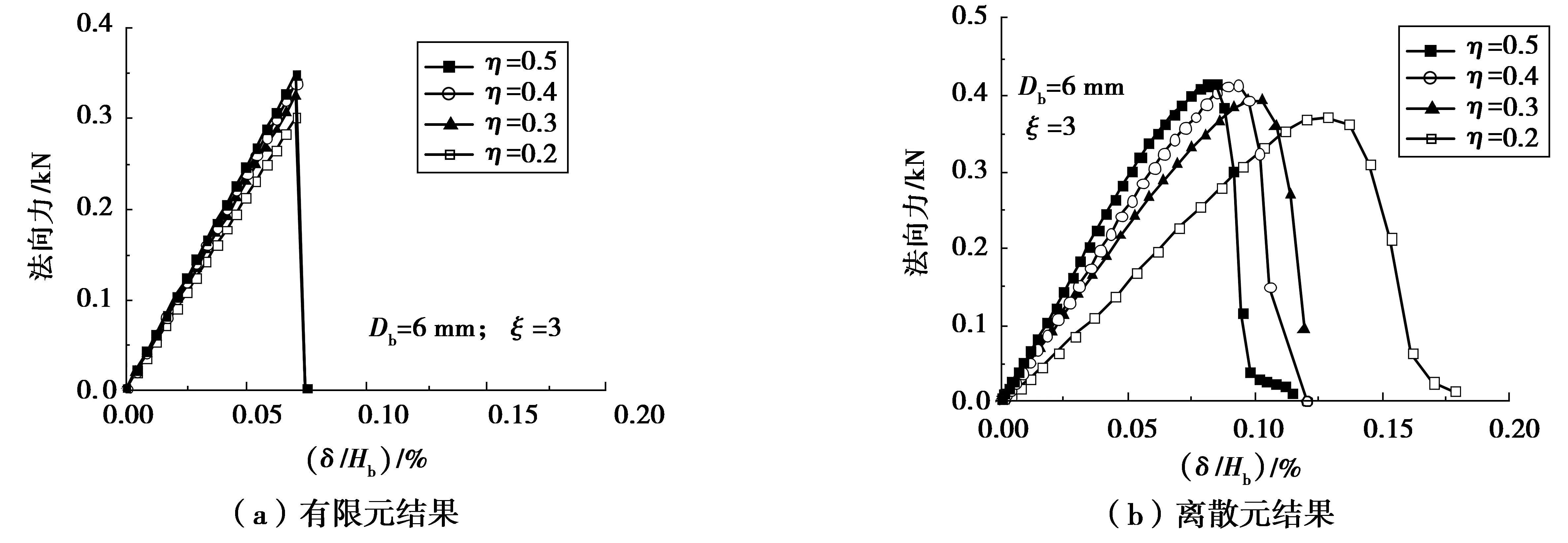
图10 不同胶结厚宽比下法向拉伸荷载与位移关系Fig. 10 Relationship between normal tensile loading and displacement at different thickness-to-width ratios of the bond

4.2 法向抗拉强度及尺寸效应

与前述类似，胶结颗粒法向抗拉强度Rt可定义为拉伸试验中的峰值拉伸荷载，相应地，可定义无量纲的胶结颗粒法向抗拉强度因子如下：

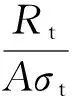
(3)

式中：σt为胶结材料单轴抗拉峰值应力，在本分析中σt=13.8 MPa(见图3的单轴拉伸试验模拟结果)。

图11为χt与胶结厚宽比η的关系曲线，χt随着η增加略有增加，趋近于1，若采用指数函数进行数据拟合，可得到最佳拟合方程为χt=e-0.036/η。因此，胶结颗粒法向抗拉强度可用以式(4)进行估算：

Rt=αηtαθt(Aσt)

(4)

式中：αηt和αθt分别为粒间胶结物的厚宽比系数和界面形状系数，αθt近似为1.0，根据本次有限元数值试验的拟合结果：αηt=e-0.036/η。

图11 抗拉强度因子与粒间胶结厚宽比关系Fig. 11 χt-η relationship obtained in FEM

图12为加载过程中胶结物水平中心截面法向拉应力分布情况，胶结中心点为横坐标原点。由图12可见，随着法向拉伸荷载增加，截面各点法向应力均有所增加，中心处应力值高于边缘处，但是中心与边缘处应力区别不如压缩试验显著，说明在拉伸荷载条件下，颗粒与胶结物接触界面约束效应并不显著。对比图12(a)和图12(c),随着η增加，应力分布趋于均匀，表明当胶结厚度超过一定范围内，端部约束影响不明显。对比图12(a)和图12(b), 随着ξ增加，应力分布区别不大，表明在拉伸荷载条件下，界面形状影响可忽略不计。

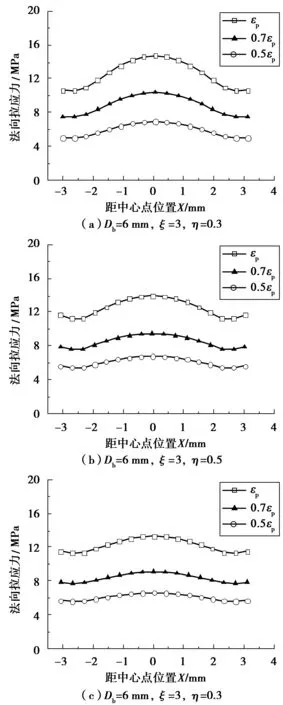
图12 胶结物水平中心截面上法向拉应力分布Fig. 12 Distribution of normal tensile stress at the horizontal central cross-section of the inter-particle cementation

5 结 论

为了研究胶结颗粒接触破坏规律及尺寸效应的影响，笔者对压缩和拉伸加载条件下的三维球形胶结颗粒进行了有限元数值试验。研究了不同直径比和厚宽比条件下胶结物抗拉压强度的变化规律，并得到考虑胶结物尺寸的胶结颗粒抗压和抗拉强度的估算公式，得到以下主要结论：

1)胶结球形颗粒法向抗压强度与粒间胶结物的几何特征显著相关，该特征可以通过两个无量纲物理量进行描述，即胶结厚宽比η和直径比ξ。胶结球形颗粒法向抗压强度随着η减小和ξ增加而增加，η的影响占主导，可以采用式(2)进行估算。

2)胶结球形颗粒法向抗拉强度的尺寸效应不是特别显著，随着η减小和ξ增加而略有增加，可采用式(4)进行估算，为简化起见可忽略ξ的影响。

需要指出的是，估算公式式(2)和式(4)所涉及的拟合公式与胶结物的材料参数有关，是否适合其它胶结材料还需要进一步的验证工作。颗粒胶结法向接触的尺寸效应不仅限于颗粒与胶结物的直径比和胶结物的厚宽比两个方面，还包括胶结颗粒之间的尺寸比，笔者只考虑了简单的等同双球的情况，在后续的研究中需进一步的完善。

[1] CUCCOVILLO T, COOP M R. On the mechanics of structured sands [J].Géotechnique，1999, 49(6):741-760.

[2] COOP M, ATKINSON J H, HUANG J T, et al. The mechanics of cemented carbonate sands[J].Géotechnique,1993,43(1):53-67.

[3] SCHNAID F, PRIETTO P, CONSOLI N. Characterization of cemented sand in triaxial compression[J].JournalofGeotechnicalandGeoenvironmentalEngineering, 2001, 127(10): 857-868.

[4] ISMAIL M, JOER H A, RANDOLPH M F, et al. Cementation of porous materials using calcite[J].Géotechnique, 2002, 52(5): 313-324.

[5] CUNDALL P A, STRACK O D L. A discrete numerical model for granular assemblies[J].Géotechnique,1979, 29(1): 47-65.

[6] DELENNE J Y, YOUSSOUFI M S E, CHERBLANC F, et al. Mechanical behavior and failure of cohesive granular materials[J].InternationalJournalforNumerical&AnalyticalMethodsinGeomechanics, 2004, 28(15):1577-1594.

[7] JIANG M J, SUN Y G, XIAO Y. An experimental investigation on the mechanical behavior between cemented granules[J].GeotechnicalTestingJournal, 2012, 35(5):104-108.

[8] JIANG M J, SUN Y G, LI L Q, et al. Contact behavior of idealized granules bonded in two different inter-particle distances: an experimental investigation[J].MechanicsofMaterials, 2012, 55(14):1-15.

[9] JIANG M J, LIU F, ZHOU Y P. A bond failure criterion for DEM simulations of cemented geomaterials considering variable bond thickness[J].InternationalJournalforNumericalandAnalyticalMethodsinGeomechanics, 2014, 38(18): 1871-1897.

[10] JIANG M J, ZHANG N, CUI L, et al. A size-dependent bond failure criterion for cemented granules based on experimental studies[J].ComputersandGeotechnics, 2015, 69: 182-198.

[11] 蒋明镜, 孙渝刚, 李立青. 复杂应力下两种胶结颗粒微观力学模型的试验研究[J]. 岩土工程学报, 2011, 33(3): 354-360. JIANG Mingjing, SUN Yugang, LI Liqing. Experimental study on micro-mechanical model for two different bonded granules under complex stress conditions[J].ChineseJournalofGeotechnicalEngineering, 2011, 33(3): 354-360.

[12] 蒋明镜, 肖俞, 孙渝刚, 等. 水泥胶结颗粒的微观力学模型试验[J]. 岩土力学, 2012, 33(5): 1293-1300. JIANG Mingjing, XIAO Yu, SUN Yugang, et al. Experimental investigation on micromechanical model of cement-bonded particles [J].RockandSoilMechanics, 2012, 33(5): 1293-1300.

[13] JIANG M J, JIN S L, SHEN Z F, et al. Preliminary experimental study on three-dimensional contact behavior of bonded granules[C]//IOPConferenceSeries:EarthandEnvironmentalScience. Warwick, UK: IOP Science, 2015.

[14] 刘芳, 李震, 蒋明镜. 粒间胶结尺寸对圆形颗粒法向接触响应的影响[J]. 地下空间与工程学报, 2015, 11(6):1450-1456. LIU Fang, LI Zhen, JIANG Mingjing. Effects of bond size on the normal contact behavior of two bonded disks[J].ChineseJournalofUndergroundSpaceandEngineering, 2015, 11(6): 1450-1456.

[15] LIU F, JIANG M J, SUN C, et al. On the size-dependent compressive resistance of bonded granules [J].GéotechniqueLetters, 2015, 5: 104-111.

[16] SHEN Z F, JIANG M, WAN R. Numerical study of inter-particle bond failure by 3D discrete element method [J].InternationalJournalforNumerical&AnalyticalMethodsinGeomechanics, 2015, 40(4):523-545.

[17] LEE J，FENVES G L. Plastic-damage model for cyclic loading of concrete structures [J].JournalofEngineeringMechanics, 1998, 124(8) : 892 -900．

(责任编辑：谭绪凯)

Formulas for Estimating Size-Dependent Normal Contact Resistance of 3D Bonded Spheres

LIU Fang1, 2, 3, ZHOU Xiangnan2, 3, JIANG Mingjing1, 2, 3

(1. State Key Laboratory of Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, P. R. China; 2. Department of Underground Architecture & Engineering, School of Civil Engineering, Tongji University, Shanghai 200092, P. R. China; 3. Key Laboratory of Geotechnical and Underground Engineering of Ministry of Education, Tongji University, Shanghai 200092, P. R. China)

The presence of inter-particle bonds leads to the unique macroscopic deformation and strength characteristics of natural structural soils. In order to study 3D cement particle contact failure regularity and size effect under the normal loading conditions, the contact mechanics test of ideal spherical particle cementation was simulated by finite element method. The results of the finite element simulation and those of discrete element simulation were compared. The finite element method was used to simulate normal contact response of two spheres sandwiching cementation in order to reveal the size effect on normal resistance of bonded spheres. The simulation results of finite element were compared with those of discrete element. The rule of compression/tension resistance of the bonded spheres was analyzed under different values of two dimensionless geometric parameters of the bond, i.e., diameter ratio and thickness-to-width ratio of the bond. Quantitative relationships between contact strength and cement size parameters were obtained. The results show that the compressive resistance of the bonded spheres is highly affected by the diameter ratio and the thickness-to-width ratio of the cementaneous material, and the thickness-to-width ratio plays a dominant role. The compressive resistance of the bonded spheres significantly decreases as the thickness-to-width ratio of the bond increases, while the size effect of the cement particle tensile strength is not significant.

geotechnical engineering; cementaneous material; contact mechanics; finite element simulation; size effect

10.3969/j.issn.1674-0696.2017.07.11

2016-02-05；

2016-12-25

国家自然科学基金项目(415722675；51239010；51579178)；国家科技支撑计划课题(2013BAB06B02)；流域水循环模拟与调控国家重点实验室自主研究课题(2015ZY05)

刘 芳(1978—)，女，广东河源人，副教授，博士，主要从事岩土力学与工程方面的研究。E-mail：liufang@tongji.edu.cn。

TU43

A

1674-0696(2017)07-066-07