基于吊索重要性的大跨度悬索桥冗余度分析

朱劲松，王 洋

(1.天津大学 建筑工程学院，天津 300072;2.天津大学 滨海土木工程结构与安全教育部重点实验室，天津 300072)



基于吊索重要性的大跨度悬索桥冗余度分析

朱劲松1,2，王 洋1

(1.天津大学 建筑工程学院，天津 300072;2.天津大学 滨海土木工程结构与安全教育部重点实验室，天津 300072)

为分析悬索桥运营期间不同吊索的失效对悬索桥冗余度的影响，以某在建大跨度悬索桥为计算实例，利用悬索桥吊索失效前后整体结构的应变能变化，确定吊索的重要性系数。依据重要性系数对吊索进行失效组合，确定组合构件的失效情况，对各类最不利损伤状况的悬索桥冗余度进行定量计算，并结合损伤结构的应力增量，提出基于吊索重要性系数的悬索桥冗余度分析方法。结果表明：越靠近跨中的吊索失效对悬索桥的冗余度影响越大，对重要性系数较大的吊索进行组合失效状况模拟，发现当冗余度小于0.201时，桥梁的应力变化巨大，且有发生整体倒塌的趋势，不再适于继续承受荷载。

桥梁工程；桥梁冗余度；大跨度悬索桥；应变能；吊索重要性系数；应力响应增量

0 引 言

桥梁冗余度是指整个桥梁体系中个别构件在使用阶段由于发生偶然荷载状况和耐久性破坏而失效时，桥梁体系的抗连续倒塌能力。悬索桥因其自身的结构特点，具有多重传力途径，其本身即具备一定的冗余度。悬索桥冗余度是桥梁体系抵抗连续倒塌能力的一种体现，是结构在初始破坏的状态下改变原有的传力路径，并达到新的稳定平衡状态的能力特征。充足的冗余度能够保证悬索桥的局部破坏不向外扩展，从而避免连续破坏或倒塌的发生。

大跨度悬索桥在受力特点、传力途径方面有着其特殊性，主梁和桥塔属于桥梁的“基础构件”，主缆是悬索桥的主要承重构件[1]，吊索作为联系主缆和主梁的“关键构件”，荷载由吊索传至主缆，再传至锚碇。悬索桥在荷载作用下具有强烈的几何非线性，当某吊索发生破坏，受力状况的改变并不是简单地剔除受损构件，而是将会按照新的传力途径，重新分配受力，对悬索桥的整体受力产生不利影响，甚至连续倒塌。为了确定悬索桥可能发生的初始最不利损伤状况，需要先对各吊索的重要性进行评估。高扬等[2]提出了适用于满应力桁架结构的计算构件重要性的方法，考虑结构本身的性质与外荷载的共同作用机制，分析了结构关键构件的刚度和强度对结构鲁棒性的共同影响。柳承茂等[3]根据最小势能原理提出了基于刚度的结构构件重要性的评估方法，证明了构件重要性与结构冗余度之间的关系。叶列平等[4]提出了考虑结合荷载形式的基于刚度理论的重要性系数评价方法，以评估构件在结构冗余度计算中的重要性。

确定了各吊索的重要性系数之后，就可以确定悬索桥的初始最不利损伤状况，继而对该损伤状况下悬索桥的冗余度进行定量计算，目前国内外对结构冗余度的研究集中在如下几个方面：M.HUSAIN等[5]采用可靠度理论，提出以冗余度强度指标(Redundancy Strength Index)和冗余度变异系数(Redundancy Variation Index)两个指标来度量结构的冗余度，并给出了确定冗余度系数及可靠性指标的计算式。U.STAROSSEK等[6]分别基于结构刚度、损伤发展和能量理论提出了不同的结构冗余度评价指标，并对其适用性进行了比较和分析。D.M.FRANGOPO等[7-8]研究了结构损伤状态与冗余系统的相互关系，提出了不确定性损伤状态对结构冗余度的影响，并基于可靠度理论和损伤评估的概念，总结了冗余度的定量计算方法，对桥梁结构系统进行安全性评价。J.D.S∅RENSEN[9]提出基于结构承载力的结构强健性评价指标，指出结构冗余度与结构强健性存在着内在关系，将结构损失前后极限承载力的比值作为该结构的强健性评价指标。另外，一些国外的规范也形成了一些指导性原则，美国联邦公路署下属的国家公路研究计划联合会(NCHRP)分别对中小跨度的常规设计桥梁的上部结构和下部结构的冗余度进行系统研究[10]，建议在桥梁设计规范中，用不同取值考虑结构体系的冗余度。

悬索桥在使用阶段的健康监测过程中，当吊索发生失效时，如果只是根据单一吊索的失效情况来对全桥的健康状况进行判别，这显然具有片面性。因此，提出基于吊索重要性系数的悬索桥冗余度分析方法，利用吊索失效前后应变能的变化量计算吊索的重要性系数，确定不同吊索失效后悬索桥的初始最不利损伤状况；综合考虑应变能灵敏度以及单根吊索的强度承载力，计算悬索桥的冗余度，结合各最不利损伤状况下悬索桥的应力响应，认为当应力增量过大或损伤前后应力激增时，该类损伤状况下的桥梁不适于继续承载。

1 悬索桥冗余度评价方法

基于冗余度分析的桥梁健康评定，须要推导出定量计算桥梁冗余度的方法，在确立悬索桥冗余度地定量计算理论时，要遵循如下几个原则。

1)选定结构冗余度的评价指标。悬索桥是一种复杂的桥梁形式，所选取的评价指标要能最大限度的体现该构件失效时对结构产生的不利影响；同时，还要保证该评价指标在计算过程中尽可能的简捷。

2)悬索桥具备复杂的传力体系，单一构件的失效会使得桥梁的受力发生整体变化，即其他未受损构件将不再与初始合理成桥状态的受力相符，进而可能出现连续性破坏。因此，有必要考虑多个构件同时失效时结构的应力状况。

3)将冗余度的定量计算结果用于桥梁的健康状况评定时，要基于结构受损后在外荷载作用下的应力响应。

基于上述原则，在计算桥梁冗余度之前，需要确定结构最有可能失效的构件，即确立初始最不利损伤状况。对于大跨度悬索桥，吊索是敏感构件，不同吊索的敏感度不尽相同。因此，首先要确定每根吊索的重要性。

采用文献[11]提出的基于应变能的分析理论，对悬索桥的各根吊索的重要程度进行评估，探究每根吊索的重要性系数，重要性系数将反应其受损后对整个结构继续承载能力的影响。不同吊索失效时结构冗余度的定量计算结果，要与损伤后结构的应力响应结合，共同对受损桥梁结构的继续承载能力进行评定。

1.1 吊索重要性系数

吊索对于悬索桥的重要性，体现在吊索损伤之后对悬索桥后续运营阶段的应力响应影响，将这种影响用应变能变化量进行定量表述。对于悬索桥系统，设其有n根吊索，根据应变能原理，结构在荷载作用下的总应变能为[11]

(1)

假设第i根吊杆发生失效，则结构总应变能：

(2)

式中：K和K+ΔK分别为吊索损伤前、后桥梁的整体刚度；r和r+Δr分别为吊索损伤前、后桥梁的位移向量。

由式(2)可得，吊索在损伤前后应变能的变化量ΔEi为

ΔEi=Ei-E

(3)

定义吊索损伤前后应变能的变化量与完好结构应变能的比值，作为吊索的重要性系数：

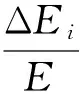
(4)

λ(i)在数值上定量的反映出第i根吊索在悬索桥的总能量分布中的贡献，即第i根吊索的损伤对全桥继续承载能力的影响程度，λ(i)定义的条件是结构发生损伤，且其取值区间为[0,1],λ(i)越大，第i根吊索的重要性也就越大。

1.2 桥梁冗余度

在定量计算出吊索的重要性系数之后，可以从所有吊索中选取影响最大的吊索进行分析，这类吊索在初始损伤的桥梁中起决定性作用。也就是说，重要性系数大的吊索损坏，将会最大限度地影响桥梁的继续承载能力，即悬索桥的冗余度。悬索桥的冗余度也可以认为是结构对于应力响应的不敏感程度，因此，在初始损伤状况下，悬索桥在荷载作用下的继续承载能力，可以通过建立应变能敏感度和吊索的承载力冗余度的数学模型而得到。

1.2.1 吊索应变能灵敏度

(5)

(6)

(7)

并定义应变能灵敏度αm,n为

αm,n=|Δem,n|/vm

(8)

式中：vm为第m根吊索的体积。

1.2.2 吊索承载能力冗余度

在研究吊索失效后桥梁剩余部分的继续承载能力时，吊索为只受拉构件，则研究其冗余度时可以利用极限承载力来定量的表述，即定义第n根吊索失效时第m根吊索的强度承载力冗余度为[11]

βm,n=1/Mm

(9)

式中：Mm为第n根吊索失效时第m根吊索的强度承载力。

1.2.3 悬索桥冗余度

利用吊索的灵敏度以及强度承载力冗余度的计算结果，可以得到悬索桥冗余度计算公式[11]：

(10)

式(10)将整体和局部同时作为悬索桥冗余度的计算参数，目的是既能从能量的角度考虑吊索受损时，全桥受力重新分配之后，新的传力体系的构成，又能从局部吊索的承载力来反应其强度储备对悬索桥冗余度的影响。

根据以上理论推导，悬索桥冗余度计算步骤可归纳为：

1)利用式(4)确定各根吊索的重要性系数αm,n。

2)根据吊索重要性系数，可以确定相应的各类初始损伤状况。不同形式的失效吊索组合决定了不同的损伤状况，即不同损伤状况下悬索桥的继续承载能力因吊索失效类型的不同而存在较大差异。

3)确定了各类单一及组合吊索失效时的初始损伤状况之后，对该损伤桥梁进行加载，分析其应力响应。

4)利用式(4)计算吊索的应变能灵敏度βm,n。

5)利用式(10)计算悬索桥的冗余度。

通过计算得到基于各类损伤状况的悬索桥冗余度，分析该类初始损伤状况的应力响应，观察其应力增量，作为用冗余度评价吊索损伤后悬索桥继续承载能力的依据。

2 悬索桥计算实例

2.1 工程背景

笔者研究背景为某在建跨度为(210+720+210)m的单跨悬索桥，加劲梁采用钢纵横梁+混凝土桥面板结合梁，中跨矢跨比为1/10.5，悬索桥主桥结构布置如图1。该桥主梁采用钢纵横梁，其材料屈服强度为345 MPa。主缆采用标准强度为1 770 MPa的预制平行钢丝索股，钢丝直径为5.25 mm，每根主缆91股，每股127丝，主缆直径为56.44 cm，两侧主缆间距为25.8 m。全桥共47对吊索，吊索采用标准强度为1 770 MPa的高强平行镀锌钢丝，纵向间距15 m。

图1 悬索桥结构立面布置Fig. 1 Elevation arrangement of a suspension bridge structure

2.2 模型建立

采用ANSYS软件建立大桥空间有限元模型，如图2，加劲梁、主塔采用Beam44单元模拟，刚臂采用Beam4单元模拟，吊索和主缆采用Link10单元模拟。悬索桥具有小变形大位移的非线性特征，有限元计算引入了单元几何刚度矩阵来考虑几何非线性方面的影响。基于研究目的，有限元模型直接以成桥状态为初始计算模型，主缆和吊索以初应变的方式施加。该悬索桥结构模型为东、西两侧对称以及上下游对称结构，因此在计算吊索重要性系数的时候只计算半跨长度内单幅索面内的吊索重要性系数，利用式(4)可以求出24根吊索的重要性系数，如表1，图3。

图2 悬索桥空间有限元模型Fig. 2 Spatial finite element model of a suspension bridge

吊索编号重要性系数吊索编号重要性系数吊索编号重要性系数吊索编号重要性系数1#吊索0.06667#吊索0.127113#吊索0.174719#吊索0.22632#吊索0.07008#吊索0.131714#吊索0.179920#吊索0.23203#吊索0.07349#吊索0.136315#吊索0.185121#吊索0.23774#吊索0.076810#吊索0.140916#吊索0.190322#吊索0.24355#吊索0.080211#吊索0.145517#吊索0.195523#吊索0.24926#吊索0.083612#吊索0.169518#吊索0.200724#吊索0.2713

图3 吊索重要性系数Fig. 3 Importance coefficients of slings

从图3可见，1～24号吊索的重要性系数各不相同，即每根吊索的失效对剩余结构的继续承载能力的影响不尽相同，从主塔向跨中依次增大。其中7#、12#、19#、24#吊索的重要性系数呈现激增现象，相比相邻吊索大幅增加。

应用式(10)可以求出24根吊索依次失效之后悬索桥的冗余度，即单根吊索断裂对结构继续承载能力的影响，如表2。根据吊索重要性系数的计算结果，对7#、12#、19#、24#吊索分别与其相邻吊索进行两两组合，计算双吊索同时损伤，对悬索桥结构继续承载能力的影响，即组合吊索失效对悬索桥冗余度的影响，结果如表3。

表2 单根吊索失效的悬索桥冗余度

表3 组合吊索失效的悬索桥结构冗余度Table 3 Redundancy of suspension under loss of combin single slings

针对重要性系数较大的23#、24#吊索的单根吊索断裂情况，以及7#、12#、19#、24#相邻吊索的组合断裂情况，分析每种情况下该类吊索在逐渐失效过程中剩余吊索的应力增量，如图4。由图4(a)可知，6#、7#吊索与7#、8#吊索两种组合失效情况的应力增量较小，而当23#与24#单独断裂失效，以及11#、12#吊索，12#、13#吊索，18#、19#吊索，19#、20#吊索，23#、24#吊索组合失效时，应力增量>150 MPa，增量极值达到275 MPa。考虑7#、12#、19#、24#吊索突然断裂的情形，即在成桥运营状态下吊索突然断裂引起的结构瞬时响应，可以将吊索内拉应力以冲击荷载的形式，反向作用在吊索锚固点处，以模拟吊索突然断裂的情况[12]。分析剩余吊索的应力响应增量，如图4(b)，可以看出吊索突然断裂，会导致相邻吊索应力激增，达到初始应力的近2倍，增量极值为580 MPa。根据冗余度计算结果以及吊索失效后损伤桥梁的应力响应可以认为，当悬索桥冗余度低于0.201时，桥梁的健康处于危险状况，不再适合继续使用，需要立即进行修复。

图4 吊索逐渐和突然失效后剩余吊索的应力响应增量Fig. 4 Stress response increment of remaining slings with the gradual and abrupt failure of slings

3 结 论

大跨度悬索桥是人类桥梁科技水平的标志，其在运营过程中的受力变化也是现今研究悬索桥的主要目标之一。用结构冗余度理论对大跨度悬索桥吊索损伤后的继续承载能力进行评估，是一种新的评价理念，国内在针对基于冗余度的损伤桥梁健康状况研究尚不成熟。笔者从能量的角度对悬索桥吊索进行重要性系数计算，确定不同吊索在其失效之时对桥梁继续承载能力的不同影响；量化悬索桥冗余度，结合损伤前后桥梁的应力增量，对吊索失效的悬索桥后续使用状况进行评价，并得出以下结论。

1)单跨悬索桥的吊索重要性从主塔向跨中方向依次增强，重要性系数越大，该吊索的失效对于悬索桥继续承载能力的减弱影响越大。

2)针对悬索桥算例，单根吊索失效状况下，悬索桥剩余结构的应变能将减小，其冗余度在0.03～1.93之间变化；利用重要性系数过大的吊索及其相邻吊索模拟组合构件失效状况，发现其冗余度急剧减小，变化范围为0.409～0.013，可知此时悬索桥结构处于极度危险状况，继续使用有可能发生大面积倒塌。

3)通过对悬索桥的冗余度进行量化计算，同时考虑吊索失效后桥梁的应力增量，综合分析认为当悬索桥冗余度低于0.201时，该桥须要立即停止使用，进行损伤检测及修复。

[1] 陈小雨，沈锐利，唐茂林．悬索桥主缆检测及承载力评估现状与发展[J]．重庆交通大学学报(自然科学版), 2013，32(增刊1)：760-763. CHEN Xiaoyu, SHEN Ruili, TANG Maolin. Current situation and development for detection and bearing capacity evaluation of main cable of suspension bridge[J].JournalofChongqingJiaotongUniversity(NaturalScience), 2013, 32(Sup1): 760-763.

[2] 高扬，刘西拉．结构鲁棒性评价中的构件重要性系数[J]．岩石力学与工程学报，2008，27(12)：2575-2584. GAO Yang, LIU Xila. Importance coefficients of components in evaluation of structure robustness[J].ChineseJournalofRockMechanicsandEngineering, 2008, 27(12): 2575-2584.

[3] 柳承茂，刘西拉．基于刚度的构件重要性评估及其与冗余度的关系[J]．上海交通大学学报，2005，39(5)：746-750. LIU Chengmao, LIU Xila. Stiffness-based evaluation of component importance and its relationship with redundancy[J].JournalofShanghaiJiaotongUniversity, 2005, 39(5): 746-750.

[4] 叶列平，林旭川，曲哲，等. 基于广义结构刚度的构件重要性评价方法[J]. 建筑科学与工程学报，2010，27(1)：1-6,20. YE Lieping, LIN Xuchuan, QU Zhe, et al．Evaluating method of element importance of structural system based on generalized structural stiffness[J]．JournalofArchitectureandCivilEngineering, 2010, 27 (1): 1-6, 20.

[5] HUSAIN M, TSOPELAS P. Measures of structural redundancy in reinforced concrete buildings I: redundancy indices[J].JournalofStructuralEngineering, 2004, 130(11): 1651-1658.

[6] STAROSSEK U, HABERLAND M. Approaches to measures of structural robustness[C]//Proceedingsofthe4thInternationalConferenceonBridgeMaintenance，SafetyandManagement,Seoul, 2008. Seoul: [s. n.], 2008.

[7] GHOSN M, FRANGOPOL D M. Redundancy and robustness of highway bridge superstructures and substructures[J].Structure&InfrastructureEngineering, 2010, 6(1/2):257-278.

[8] FRANGOPOL D M. Effects of damage and redundancy on structural performance[J].ArchivesInternationalesDePharmacodynamieEtDeTherapie, 1987, 66(10): 100-107.

[9] S∅RENSEN J D. Framework for robustness assessment of timber structures[J].EngineeringStructures, 2011, 33(11): 3087-3092.

[10] GHOSN M, MOSES F, OFFICIALS T.RedundancyinHighwayBridgeSuperstructures[R].Washington:National Academy Press,1998.

[11] 黄冀卓，王湛．钢框架结构鲁棒性评估方法[J]．土木工程学报，2012 ，45(9)：45-54. HUANG Jizhuo, WANG Zhan. An approach for evaluation of the structural robustness of steel frames[J].ChinaCivilEngineeringJournal, 2012, 45(9): 45-54.

[12] 朱劲松，邑强．拱桥新型吊杆安全性及其静动力影响研究[J]．桥梁建设，2011 (1)：39-42. ZHU Jinsong, YI Qiang. Study of safety of new type suspenders and their static and dynamic performance influences of arch bridge[J].BridgeConstruction, 2011(1): 39-42.

(责任编辑：谭绪凯)

Redundancy Analysis on Long-Span Suspension Bridge Based on Sling Importance

ZHU Jinsong1, 2, WANG Yang1

(1. School of Architecture Engineering, Tianjin University, Tianjin 300072, P. R. China;2. Key Laboratory of Coast Civil Structure & Safety, Ministry of Education, Tianjin University, Tianjin 300072, P. R. China)

To analyze the impact of the failure of different slings on bridge redundancy in the operation of a suspension bridge, a long-span suspension bridge being in construction was taken as example. By use of the variation of strain energy of the whole structure before and after the failure of slings of the suspension bridge, the importance coefficients of slings were determined. According to the importance coefficient, the failure slings were combined, and the failure condition of components were determined. And then, the quantitative calculation of the suspension bridge redundancy under the most adverse damage conditions was carried out. Combined with the stress increment of the damaged structure, the redundancy analysis method of a suspension bridge based on the sling importance coefficient was put forward. The results show that: when the sling failure is closer to the mid-span, its effect on long-span suspension redundancy is bigger. The failure condition of sling combinations with the bigger important coefficients is simulated. It is founded that when the redundancy is less than 0.201, the stress response of a long-span suspension bridge is enormous; and the bridge has a trend of total structural collapse, which is no longer available to bear the load.

bridge engineering; bridge redundancy; long-span suspension bridge; strain energy; importance coefficient of sling; stress response increment

10.3969/j.issn.1674-0696.2017.07.01

2016-05-06；

2017-01-02

国家自然科学基金项目(51578370)；天津市应用基础与前沿技术研究计划项目(14JCYBJC21500)

朱劲松(1975—)，男，安徽滁州人，博士，教授，博士生导师，主要从事桥梁损伤识别、健康监测、全寿命可靠度评定及桥梁抗疲劳设计等方面的研究。E-mail：jszhu@tju.edu.cn。

U448.25；U443.28

A

1674-0696(2017)07-001-06