伪补MS代数的理想与滤子同余关系的注记

赵秀兰，吕凤姣，陈丽娟

（1.黄河科技学院数理部，河南 郑州，450063；2.河南工程学院理学院，河南 郑州，450007）

ZHAO Xiulan1,LÜ Fengjiao1,CHEN Lijuan2

（1.Department of Mathematics and Physics,Huanghe Science and TechnologyCollege,Zhengzhou 450063,Henan,China; 2.Henan Institute of Engineering,Zhengzhou 450007,Henan,China）

伪补MS代数的理想与滤子同余关系的注记

赵秀兰1，吕凤姣1，陈丽娟2

（1.黄河科技学院数理部，河南 郑州，450063；2.河南工程学院理学院，河南 郑州，450007）

依据伪补MS代数的核理想及余核滤子判别定理以及核理想和余核滤子所生成的同余关系表达式，研究了伪补MS代数的核理想和余核滤子同余关系的同余置换性，证明了伪补MS代数核理想格和余核滤子格是同构的.

Ockham代数；伪补代数；伪补MS代数；核理想；余核滤子；同构

0引言

在泛代数研究领域，对代数结构的研究，一直是本专业学者关注的方向.理想和滤子是人们认识Ockham代数类的结构及同余关系的一个重要工具，特别是核理想与余核滤子的同余关系反映Ockham代数类的结构.在文献[1-8]中，作者在相应的代数类上引入理想与滤子，以理想与滤子为载体刻画代数结构.文献[4-5]研究了伪补MS代数的理想和滤子，给出了伪补MS代数具有核理想和余核滤子同余关系表达式以及核理想和余核滤子判别定理.文献[9]首次引入伪补MS代数的概念，在这篇文献中，作者定义了伪补MS代数，描述了伪补MS代数的运算性质，给出了伪补MS代数的主同余表示定理（伪补MS代数的详细信息见文献[10-12]）.本文作为文献[4-5]的一个补充，在伪补MS代数的理想和滤子已有结论的基础上，进一步讨论伪补MS代数核理想与余核滤子同余关系的性质.

1 基本知识

定义1.1[13]设（L；∧，∨）是一个格，I是格L的子格，若x，y∈L，y≤x∈I总有y∈I，称子格I是格L的理想.对偶地，F是格L的子格，若x，y∈L，y≥x∈F总有y∈F，称子格F是格L的滤子.

便于阐述，沿用文献[13]中的符号，记I（L），F（L）分别代表L的全体理想和全体滤子所构成的集合.设I，J∈I（L），F1，F2∈F（L），定义

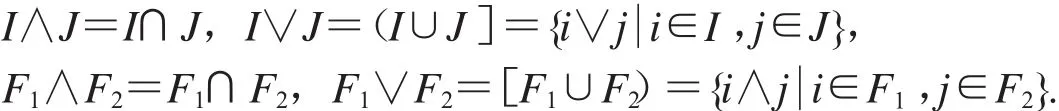
定义1.2[10]设（L；∧，∨，0，1）是一个有界分配格，其上赋予一个一元运算o，且满足下列条件：

（1）（∀x∈L）x≤xoo；

（2）（∀x，y∈L）（x∧y）o＝xo∧yo；

（3）1o＝0.

称（L；∧，∨，o，0，1）为MS代数.

定义1.3[11-12]一个伪补代数（简称p-代数）是一个代数（L；∧，∨，*，0，1），它具有一个最小元0及一个映射*：L→L使得x*＝max{y∈L∧y＝0}.

定义1.4[9]设（L；∧，∨，0，1）是一个有界分配格，其上赋予两个一元运算*和o，其中（L；*）是p-代数，（L；）°是MS-代数，并且一元运算*和o满足条件（x∈L）x*°＝x°*，称（L；∧，∨，*，o，0，1）是伪补MS-代数（简称pMS-代数）.

定义1.5[9]设（L；∧，∨，*，o，0，1）是pMS-代数，θ是L的一个格同余关系，若

（x，y）∈θ⇒（x*，y*）∈θ，（（fx），（fy））∈θ，

则称θ是L的同余关系.符号ConL表示L的全体同余关系构成的集合.

定义1.6[11-12]设（L；∧，∨，*，o，0，1）是pMS-代数，对于L的理想I，若存在L的一个

对于L的滤子F，若存在L的一个同余关系φ，使得F＝Cokerφ，其中

称滤子F为L的余核滤子.

引理1.1[9]设（L；∧，∨，*，o，0，1）是pMS-代数，则有下列结论：

（1）（∀a∈L）ao*o＝a*oo＝aoo*＝a*；

（2）（∀a∈L）a*o*＝ao**＝a**o＝ao；

（3）（∀a∈L）a**＝aoo；

（4）（∀a，b∈L）（a∧b）*＝a*∨b*

现给出pMS-代数核理想，余核滤子的判别定理.

引理1.2[4-5]设（L；∨，∧，*，o，0，1）是一个pMS-代数，I是L的理想，F是L的滤子，则

（1）I是L的核理想，当且仅当（a∈L）a∈I⇒{a**，a*°}⊆I；

（2）F是L的余核滤子当且仅当（∀a∈L）a∈F⇒a*°∈F.

设L是pMS-代数，符号KI（L）表示L的全体核理想构成的集合.符号CokF（L）表示L的全体余核滤子构成的集合.

引理1.3[4-5]

（1）设L是pMS-代数，则K（IL）是（IL）的子格.

（2）设L是pMS-代数，CokF（L）是F（L）的子格.

引理1.4[4]设（L；∨，∧，*，o，0，1）是pMS-代数，I是L的核理想，则下列命题等价：

（1）（x，y∈L）（x，y）∈θ（I）；

（2）（∃i∈I）x∨i＝y∨i；

（3）（∃i，j∈I）（x∨i）∧j*＝（y∨i）∧j*.

引理1.5[5]设（L；∨，∧，*，o，0，1）是一个pMS-代数，F是L的余核滤子，则（x，y）∈θ（F）⇔（∃a，b∈F）（x∧a）∨b°＝（y∧a）∨b°.

引理1.6设（L；∨，∧，*，°，0，1）是一个pMS-代数，F是L的余核滤子，则下列命题等价：

（1）（x，y∈L）（x，y）∈θ（F）；

（2）（∃i∈F）x∧i＝y∧i；

（3）（∃a，b∈F）（x∧a）∨b°＝（y∧a）∨b°.

证明 由引理1.5知，（1）与（3）等价.易见，（2）⇒（3），下证（3）⇒（2）.

假设（3）成立，则（∃a，b∈F）（x∧a）∨b°＝（y∧a）∨b°.由引理1.1知，b°＝b°**，故

[（x∧a）∨b°**]∧b°*＝[（y∧a）∨b°**]∧b°*，根据分配性及b°**∧b°*＝0，可得x∧a∧b°*＝y∧a∧b°*.由引理1.2知，b°*∈F，又因a∈F，从而a∧b°*∈F，所以（2）成立.

设（L；∨，∧，*，o，0，1）是一个pMS-代数，I是L的核理想，F是L的余核滤子，在L上定义一个等价关系RI和RF如下：（x，y）∈RI⇔（∃i∈I）x∨i＝y∨i；（x，y）∈RF⇔（∃i∈F）x∧i＝y∧i.

在文献[4]和[5]中，已论证过RI∈ConL，RF∈ConL且I＝KerRI，F＝KerRF.

在第2部分，将分别探讨核理想与余核滤子及其对应的核理想同余关系与余核滤子同余关系之间的同构关系，伪补MS代数核理想格与其余核滤子格的同构关系.

2 主要结果

定理2.1设（L；∨，∧，*，o，0，1）是1个pMS-代数，则

（1）（I，J∈K（IL））I≤J⇔RI≤RJ；

（2）（F1，F2∈CokF（L））F1≤F2⇔RF1≤RF2

证明（1）设I，J∈K（IL），I≤J，由RI，RJ的定义知，RI≤RJ.

另一方面，设I，J∈KI（L），RI≤RJ，则KerRI≤KerRJ.由文献[4]知，I＝KerRI，J＝KerRJ，所以I≤J.

（2）设F1，F2∈CokF（L），由RF1，RF2的定义知，若F1≤F2，则RF1≤RF2.

另一方面，设F1，F2∈CokF（L），由文献[5]知，F1＝CokerRF1F2＝CokerRF2.所以，若RF1≤RF2，CokerRF1≤CokerRF2，故RF1≤RF2.

设L是pMS代数，θ，φ∈ConL，定义L上的一个等价关系.

（x，y）∈θφ⇔（∃z∈L）（x，z）∈θ，（z，y）∈φ.

易见，θφ是L上的同余关系.

若θ，φ∈ConL，且θ，φ满足关系式θφ＝φ θ，则称同余关系θ，φ具有同余置换性.

对于任意的I1，I2∈K（IL），F1，F2∈CokF（L），则RI1，RI2及RF1，RF2具有同余置换性.

定理2.2设（L；∨，∧，*，°，0，1）是1个pMS-代数，I，J∈K（IL），F1，F2∈CokF（L），则

（1）RIRJ＝RJRI；

（2）RF1RF2＝RF2RF1.

证明（1）令（x，y）∈RIRJ，则存在z∈L，使得（x，z）∈RI，（z，y）∈RJ.于是存在

i∈I，j∈J使得x∨i＝z∨i，z∨j＝y∨j.

所以x∨i∨j＝y∨i∨j

令t＝（x∨j）∧（y∨i），则

x＝x∧（x∨i∨j）≡RJ（x∨j）∧（x∨i∨j）＝（x∨j）∧（y∨i∨j）≡RJ（x∨j）∧（y∨i）.

所以，（x，t）∈RJ.

又因

t∨i＝（（x∨j）∧（y∨i））∨i＝（x∨i1∨i2）∧（y∨i1）＝i∨（（x∨i∨j）∧y），所以

即t≡RIy.因此（x，y）∈RJRI，从而得到RIRJ≤RJRI.类似地，可得到相反的不等式，因此（1）成立.（2）假设（x，y）∈RF1RF2，则存在z∈L，使得（x，z）∈RF1，（z，y）∈RF2，则存在f1∈F1，f2∈F2，有x∧f1＝z∧f1，z∧f2＝y∧f2.所以x∧f1∧f2＝y∧f1∧f2.

令s＝（x∧f2）∨（y∧f1），从而可得

因此，（x，s）∈RF2.

又因s∧f1＝（x∧f1∧f2）∨（y∧f1）＝（[x∧f1∧f2）∨y]∧f1，

所以s≡RF1（x∧f1∧f2）∨y＝（y∧f1∧f2）∨y＝y.

即s≡RF1y.所以（x，y）∈RF2RF1，从而得到RF1RF2≤RF2RF1.

类似地，可得到相反的不等式，因此（2）成立.

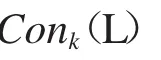
定理2.3

（1）K（IL）≅Con（kL）；

（2）CokF（L）≅Con（FL）.

证明（1）先证I，J∈KI（L），有RI∧RJ＝RI∧J.由引理1.3知，I∧J∈KI（L）.又因I∧J≤I，I∧J≤J，故由定理2.1知，RI∧J≤RI，RI∧J≤RJ，所以RI∧J≤RI∧RJ.

设（x，y）∈RI∧RJ，由文献[13]知，（x，y）∈RI且（x，y）∈RJ，则存在i∈I，j∈J使得x∨i＝y∨i，x∨j＝y∨j.从而（x∨i）∧（x∨j）＝（y∨i）∧（y∨j）.于是x∨（i∧j）＝y∨（i∧j）.又因i∧j∈I∧J，故（x，y）∈RI∧J，所以RI∧RJ≤RI∧J.因此RI∧RJ＝RI∧J.

再证对任意的I，J∈KI（L），有RI∨RJ＝RI∨J.由引理1.3知，I∨J∈K（IL）.

注意到I∨J≥I，I∨J≥J，由定理2.1知，RI∨J≥RI，RI∨J≥RJ，所以RI∨J≥RI∨RJ.

设（x，y）∈RI∨J，则存在i∈I及i∈J使x∨i∨j＝y∨i∨j，从而有

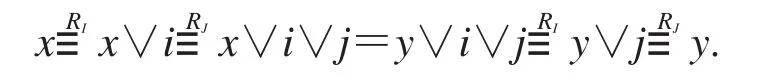
故（x，y）∈RI∨RJ，所以有RI∨J≤RI∨RJ，因此RI∨RJ＝RI∨J.

又因RI＝RJ当且仅当I＝KerRI＝KerRJ＝J，所以映射：I→RI建立起K（IL）→Con（kL）的一一对应，所以K（IL）≅Con（kL）.（2）对偶地，可证CokF（L）≅Con（FL）.

设L是pMS代数，对于L的每一个余核滤子F和核理想I，记集合，β（F）＝{x∈（∃a∈F）x≤ao}，α（I）＝{x∈L（∃a∈I）x≥a*}.

定理2.4设（L；∨，∧，*，o，0，1）是1个pMS-代数，又设I及F分别是L的核理想与余核滤子，则

（1）α（I）是L的余核滤子；

（2）β（F）是L的核理想.

证明（1）易得，α（I）是L的滤子.设x∈α（I），则存在a∈I，使得

由引理1.2知，I是L的核理想，则a*o∈I，所以x*o∈α（I）.又有引理1.2可得，α（I）是L的余核滤子.

（2）显然，β（F）是L的理想.设x∈β（F），则存在a∈F，使得

x≤ao，x**≤ao**＝（a*）*o，x*o≤ao*o＝（ao）*o，

由引理1.2知，a**，a*o∈F.所以x**，x*o∈β（F）.又有引理1.2得，β（F）是L的核理想.

根据RI，RF的定义，那么，余核滤子α（I）和核理想β（F）的同余关系将与核理想I与余核滤子F之间建立下列等式关系.

定理2.5设（L；∨，∧，*，o，0，1）是1个pMS-代数，I是L的核理想，则θ（I）＝θ（α（I））.

证明 设（x，y）∈θ（I），由引理1.4知，则有（∃i∈I）x∨i＝y∨i，从而得

根据分配性及i∧i*＝0，故x∧i*＝y∧i*.又因i*∈α（I），故由引理1.6知，（x，y）∈θ（α（I））.所以θ（I）⊆θ（α（I））.

另一方面，设（x，y）∈θ（α（I）），由引理1.5知，存在a，b∈α（I），使得

（x∧a）∨b°＝（y∧a）∨b°.由于a，b∈α（I），则存在i，j∈I，有a≥i*，b≥j*，从而bo≤j*o.故（x∧a）∨j*o＝（y∧a）∨j*o.根据分配性得

故

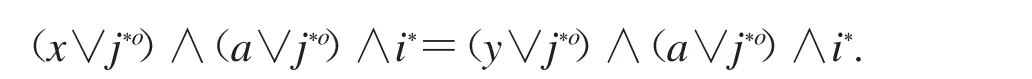
因为a≥i*，所以

由于j*o，i∈I，由引理1.4知，（x，y）∈θ（I）.所以θ（α（I））⊆θ（I）.因此θ（I）＝θ（α（I））.

对于θ（β（F）），θ（F），不存在关系式θ（β（F））＝θ（F），只满足如下关系式.

定理2.6 θ（β（F））⊆θ（F）.

证明 设（x，y）∈θ（β（F）），由引理1.4知，存在a，b∈β（F），（x∨a）∧b*＝（y∨a）∧b*.由a，b∈β（F），存在i，j∈F，使得a≤io，b≤jo.所以

故

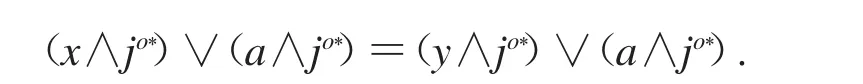
从而（x∧jo）*∨io＝（y∧jo）*∨io.故由引理4知，（x，y）∈θ（F），所以θ（β（F））⊆θ（F）.

下面，举反例说明θ（F）⊄θ（β（F））.设（L；∨，∧，*，°，0，1）是1个pMS-代数，如图1所示.

令F＝{a，1}，由β（F）的定义知，β（F）＝{0}.易见（a，1）∈θ（F），但（a，1）∉θ（β（F））.若（a，1）∈θ（β（F）），则a∨0＝1∨0＝1，故a＝1，此a≠1与相矛盾，故θ（F）⊄θ（β（F））.

定理2.7（1）β（α（I））＝I；（2）α（β（F））＝F.

证明（1）由定理2.4知，β（α（I））是L的核理想.设x∈β（α（I）），当且仅当存在a∈α（I），使得x≤ao.由a∈α（I），当且仅当存在i∈I，使得a≥i*，所以x≤i*o.由引理1.2知，i*o∈I，从而x∈I，故β（α（I））＝I.

（2）由定理2.4知，α（β（F））是L的余核滤子.设x∈α（β（F）），当且仅当存在a∈β（F）使得x≥a*.由a∈β（F），当且仅当存在j∈F，使得a≤jo，即x≥jo*.由引理1.2知，jo*∈F，从而x∈F，故α（β（F））＝F.

设L是pMS代数，对于L的核理想集KI（L）和余核滤子集CokF（L），有下列定理.

定理2.8 KI（L）≅CokF（L）.

证明 定义映射f∶KI（L）→CokF（L）和映射g∶CokF（L）→KI（L），使得

∀I∈KI（L），f（I）＝α（I），

∀F∈CokF（L），g（F）＝β（F）.设I1，I2∈KI（L），F1，F2∈CokF（L），由引理1.3知，

I1∧I2，I1∨I2∈KI（L），F1∧F2，F1∨F2∈CokF（L）.

又由定理2.4知，

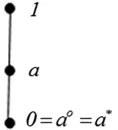
图1

由定理2.3和定理2.8，易得下列结论.

推论2.1 Conk（L）≅KI（L）≅CokF（L）≅ConF（L）.

3 结论

本文在文献[4]和[5]的基础上，利用伪补MS代数的核理想和余核滤子判别定理以及它们的同余关系表达式，论证了伪补MS代数的核理想和余核滤子同余关系的同余置换性，获得

了伪补MS代数核理想格和余核滤子格同构的结论.这一结论有助于我们了解伪补MS代数的结构，同时丰富了序代数结构的研究.

[1]罗从文.MS-代数的核理想[J].应用数学，2001，14（1）：39-41.

[2]黎爱平.分配P-代数的核理想[J].赣南师范学院学报，2006，27（3）：32-33.

[3]朱怡权.双重stone代数的主同余关系[J].纯粹数学与应用数学，2006，22（4）：520-525.

[4]赵秀兰，刘洁.伪补MS-代数的核理想与同余关系[J].江西师范大学学报（自然科学版），2014（6）：565-568.

[5]赵秀兰，马红娟.伪补MS-代数的滤子同余关系[J].纯粹数学与应用数，2014，30（3）：255-263.

[6]张小红，刘三阳，刘用麟.伪MIL-代数（WPBL-代数）的正则滤子[J].西安电子科技大学学报（自然

科学版），2006，23（5）：829-832.

[7]牛超群，吴洪博.BR0代数中的*理想及其诱导的商代数[J].江西师范大学学报（自然科学版），2013，37（3）：221-224.

[8]赵秀兰，初元红，史西专.双重伪补Ockham代数的理想与滤子同余关系的注记[J].汕头大学学报（自然科学版），2016，31（1）：35-40.

[9]FANG J.Pseudocomplemented MS-algebras[J].Algebra Colloq，2013，3（1）：491-500.

[10]BLYTH TS，VARLETJ C.On a common abstraction ofde Morgan algebras and Stone algebras[J].Proc Roy Soc Edinburgh，1983，94（94）：301-308.

[11]BLYTH T S，VARLET J C.Ockham algebras[M].Oxford：Oxford University Press，1994.

[12]FANG J.Distributive lattices with unary operations[M].北京：科学出版社，2011.

[13]GRÄTZER G.Lattice theory[M].NewYork：W H Freeman and Company，1971.

A Note on the Ideal and Filter Congruence Relations on Pseudo Complement MS Algebras

By using the discriminant theorem of kernel ideals and co-kernel filters on pseudo complemented MS algebras,the expression of the kernel ideals,co-kernel filters congruence relations are obtained.It is shown that the congruence permutation of kernel ideals and co-kernel filters,the lattice of kernel ideals and the lattice of co-kernel filters are isomorphic.

Ockham algebra;pseudo complemented algebra;pseudo complement MS algebra; kernel ideal;co-kernel filter;isomorphism

ZHAO Xiulan1,LÜ Fengjiao1,CHEN Lijuan2

（1.Department of Mathematics and Physics,Huanghe Science and TechnologyCollege,Zhengzhou 450063,Henan,China; 2.Henan Institute of Engineering,Zhengzhou 450007,Henan,China）

O151

A

1001-4217（2017）03-0022-07

2016-08-26

赵秀兰（1982—），女，河南周口人，副教授，硕士，研究方向：格论与序代数.E-mail：xiulanz@126.com.

国家自然科学基金资助项目（11302072）.