格蕴涵代数的Ω-模糊子代数*

傅小波，廖祖华

1.无锡职业技术学院，江苏 无锡 214121

2.江南大学 理学院，江苏 无锡 214122

格蕴涵代数的Ω-模糊子代数*

傅小波1，廖祖华2+

1.无锡职业技术学院，江苏 无锡 214121

2.江南大学 理学院，江苏 无锡 214122

+Corresponding author:E-mail:liaozuhua57@aliyun.com

FU Xiaobo,LIAO Zuhua.Ω-fuzzy subalgebra in lattice implication algebra.Journal of Frontiers of Computer Scienceand Technology,2017,11(7)：1183-1190.

给定一个集合Ω，将Ω-模糊集与格蕴涵代数相结合，引入了格蕴涵代数Ω-模糊子代数的概念，并研究了其相关性质；给出了格蕴涵代数Ω-模糊子代数的若干等价刻画，讨论了格蕴涵代数Ω-模糊子代数与格蕴涵代数子代数之间的相互关系；研究了格蕴涵代数Ω-模糊子代数在Ω-模糊集下交、并等运算下的基本性质；讨论了格蕴涵代数Ω-模糊子代数的同态像与同态原像的基本性质；最后研究了格蕴涵代数Ω-模糊子代数的直积与投影。

格蕴涵代数；模糊Ω-子代数；同态；直积

1 引言

1965年，美国著名的控制论专家Zadeh提出了模糊集的概念[1]，目前，模糊集的思想已经被广泛应用于数学的各个领域。1971年，Rosenfeld将模糊集的思想与群相结合，在文献[2]中提出了模糊子群的概念，开创了模糊代数的研究新领域。1975年，Zadeh对模糊集做了进一步的推广，在文献[3]中提出了区间值模糊集。1980年，刘应明在文献[4-5]中提出了模糊点和模糊集间的“∈（属于）”和“q（重于）”关系。1992—1996年Bhakat和Das利用模糊点和模糊集间的“∈（属于）”和“ q（重于）”关系，给出了(∈,∈∨q)-模糊子群的定义，并研究相关的性质[6-8]。2006年，廖祖华等人把模糊点和模糊集间的“q（重于）”关系推广为“q(λ,μ)（广义重于）”关系，获得许多有意义的结果[9-11]。2001年，Young等人在文献[12]中提出了Ω-模糊集，并将其与BCK/BCI代数相结合，给出BCK/BCI代数的Ω-模糊理想的概念。2008年，彭家寅对Ω-模糊集做了进一步的研究，先后给出了BCI代数的Ω-模糊 p-理想和Ω-模糊H-理想的概念，BCH-代数的Ω-模糊正定关联理想的概念，以及BCH-代数的Ω-模糊点理想的概念等[13-16]。2013年，廖祖华等人将Ω-模糊集与群和环相结合，并对相关的性质进行了研究，获得了许多有意义的结果[17-20]。同年，刘卫锋将Ω-模糊集应用于布尔代数，给出了Ω-模糊子代数的概念[21]。2015年，汤华晶等人将Ω-模糊集与软集理论相结合，提出了Ω-模糊软环的概念[22]。

1993年，徐扬在Fuzzy蕴涵代数[23]基础上引入格蕴涵代数的概念[24]。2003年，徐扬等人将格蕴涵代数相关的研究成果在德国施普林格出版社出版了专著[25]。随后，众多学者对格蕴涵代数做了进一步的研究，获得了许多有意义的结果[26-29]。本文将Ω-模糊集的思想和方法应用于格蕴涵代数，提出了格蕴涵代数的Ω-模糊子代数的概念，得到了一些有意义的结果。

2 预备知识

定义1[25]设 (L,∨,∧,',→,O,I)是有界格，O 是最小元，I是最大元，':L→L是格中偏序≤的逆序对合对应，→:L×L→L是一个映射。称(L,∨,∧,',→,O,I)是一个格蕴涵代数，如果∀x,y,z∈L，满足下列条件：

（1）x→(y→z)=y→(x→z)

（2）x→x=I

（3）x→y=y'→x'

（4）若 x→y=y→x=I，则 x=y

（5）(x→y)→y=(y→x)→x

（6）(x∨y)→z=(x→z)∧(y→z)

（7）(x∧y)→z=(x→z)∨(y→z)简称为L是格蕴涵代数。

引理1[25]设L是格蕴涵代数，∀x,y∈L，则：

（1）O→x=I,x→I=I,I→x=x,x→O=x'

（2）x≤y当且仅当x→y=I

（3）x∨y=(x→y)→y

定义2[25]设A⊆L，称A是L的一个格蕴涵子代数，如果满足下列条件：

（1）(A,∨,∧,')是 (L,∨,∧)的带有逆序对合 '有界子格；

（2）若 x,y∈A，则有 x→y∈A。

引理2[25]L是格蕴涵代数，A是L的一个非空子集，则A是L的一个格蕴涵子代数，如果∀x,y∈L，满足下列条件：

（1）O∈A

（2）若 x,y∈A，则x→y∈A

定义3[25]L是格蕴涵代数，称L非空子集A是L的一个模糊格蕴涵子代数，如果∀x,y∈L，满足下列条件：

（1）A(I)=A(O)

（2）A(x→y)≥A(x)∧A(y)

引理3[24]设A是L的一个模糊格蕴涵子代数，则∀x∈L，A(I)=A(O)≥A(x)。

定义4[25]设L、M是格蕴涵代数，称蕴涵同态f:L→M为格蕴涵同态，如果∀x,y∈L，满足下列条件：

（1）f(x→y)=f(x)→f(y)

（2）f(x∨y)=f(x)∨f(y)

（3）f(x∧y)=f(x)∧f(y)

（4）f(x')=(f(x))'

设映射 f:L→M为格蕴涵同态，若 f是单射，则称 f是单同态；若 f是满射，则称 f是满同态；若 f是双射，则称 f是同构。

引理4[25]设L、M是格蕴涵代数，映射 f:L→M为满格蕴涵同态，则 f(O)=O。

定义5[25]设 L1、L2是格蕴涵代数，规定(L1×L2,∨,∧,',→,O,I)的运算如下：∀x,y∈L1×L2,x=(x1,x2),y=(y1,y2)，其中 xi,yi∈Li(i=1,2)。

（1）x∧y=(x1∧x2,y1∧y2)

（2）x∨y=(x1∨x2,y1∨y2)

（3）x'=(x1',x2')

（4）x→y=(x1→x2,y1→y2)

（5）O=(O,O),I=(I,I)

引理5[25]L1×L2在定义5运算规定下构成一个格蕴涵代数。称L1×L2为格蕴涵代数L1、L2的乘积格蕴涵代数，简称为直积。

定义6[29]设 A、B分别是格蕴涵代数L1、L2的模糊子集，∀(x,y)∈L1×L2，定义映射

则A×B是L1×L2的模糊子集，并称A×B为A、B的直积。

定义7[17]设X为论域，Ω为非空给定集合，映射A:X×Ω→[0,1]称为X的Ω-模糊集。

3 格蕴涵代数的Ω-模糊子代数

下面给出格蕴涵代数L的Ω-模糊子代数的概念，并研究它们的等价刻画及其相关的性质。

定义8设A:L×Ω→[0,1]是格蕴涵代数L的Ω-模糊集，称A是格蕴涵代数L的Ω-模糊子代数，如果∀δ∈Ω ，∀x,y∈L，满足下列条件：

（1）A(O,δ)≥ A(x,δ)

（2）A(x→ y,δ)≥A(x,δ)∧A(y,δ)

定理1设A:L×Ω→[0,1]是格蕴涵代数L的Ω-模糊集，A是格蕴涵代数L的Ω-模糊子代数，则∀δ∈Ω ，∀x,y∈L，有下列性质成立：

（1）A(I,δ)=A(O,δ)≥ A(x,δ)

（2）A(x,δ)=A(x',δ)

（3）A(x∨ y,δ)≥A(x,δ)∧A(y,δ)

（4）A(x∧ y,δ)≥A(x,δ)∧A(y,δ)

证明（1）∀δ∈Ω,∀x∈L，一方面，因为 A是格蕴涵代数 L 的 Ω-模糊子代数，故 A(O,δ)≥A(x,δ)，取x=I，则 A(O,δ)≥ A(I,δ)；另一方面，A(I,δ)=A(O → O,δ)≥A(O,δ)∧ A(O,δ)=A(O,δ)，综上所述，A(I,δ)=A(O,δ)≥A(x,δ)。

（2）∀δ∈Ω ，∀x∈L，因为 A是格蕴涵代数 L的Ω-模糊子代数，由引理1可知，一方面，A(x,δ)=A(I→ x,δ)=A(x'→ I',δ)=A(x'→ O,δ)≥ A(x',δ)∧ A(O,δ)=A(x',δ)；另一方面，A(x',δ)=A(x→O,δ)≥A(x,δ)∧A(O,δ)=A(x,δ)，综上所述，A(x,δ)=A(x',δ)。

（3）∀δ∈Ω ，∀x,y∈L，因为 A是格蕴涵代数L的Ω-模糊子代数，所以由引理1可知，A(x∨y,δ)=A((x→ y)→y,δ)≥A(x→ y,δ)∧A(y,δ)≥(A(x,δ)∧A(y,δ))∧A(y,δ)=A(x,δ)∧ A(y,δ)。

（4）∀δ∈Ω ，∀x,y∈L，A是格蕴涵代数L的 Ω-模糊子代数，因此由引理1及定理1的（2）和（3）可知，A(x∧ y,δ)=A((x∧ y)',δ)=A(x'∨ y',δ)≥ A(x',δ)∧ A(y',δ)=A(x,δ)∧A(y,δ)。 □

例1设L={O ,a,b,I} ，L上的运算 ∨、∧、→ 和′的定义如表1～表4，则L={O ,a,b,I}是一个格蕴涵代数[25]。

（1）L的模糊集A1:L→[0,1]，若令：

则A1是L的满足定义2的模糊格蕴涵子代数；给定一个模糊集 Ω ，∀δ∈Ω，∀x∈L，A:L×Ω→[0,1]，若令A(x,δ)=A1(x)，则 A同样是L的满足定义8的Ω-模糊子代数。

（2）L的模糊集A2:L→[0,1]，若令：

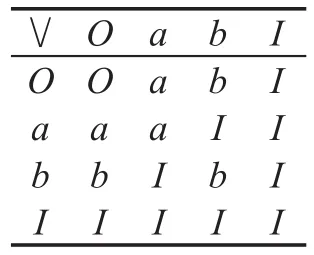
Table1 Operator“ ∨ ”表1 运算“∨”

Table2 Operator“ ∧ ”表2 运算“∧”

Table 3 Operator“ → ”表3 运算“→”

Table 4 Operator“ '”表4 运算“'”

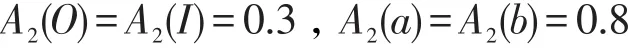
则A2不是L的满足定义3的模糊格蕴涵子代数；给定一个模糊集 Ω={0.6,0.4}，∀δ∈Ω，∀x∈L,A:L×Ω→[0,1]，若令：

则A是L的满足定义8的Ω-模糊子代数。

由例1可知，Ω-模糊子代数是一种全新的代数结构，不同于现有的模糊子代数。模糊子代数是Ω-模糊子代数的一种特殊形式(A(x,δ)=A(x))。下面来研究Ω-模糊子代数相关的性质。

定理2设A:L×Ω→[0,1]是格蕴涵代数L的Ω-模糊集，A是格蕴涵代数L的Ω-模糊子代数⇔∀λ∈是格蕴涵代数L的子代数，其中

证明“ ⇒ ”∀δ∈Ω ，因为，所以存在，即 A(x0,δ)≥λ。因为 A是格蕴涵代数 L的Ω-模糊子代数，所以 A(O,δ)≥A(x,δ)≥λ，即；若且，则 A(x,δ)≥λ 且 A(y,δ)≥λ ，从而A(x→y,δ)≥A(x,δ)∧A(y,δ)≥λ，A(x→y,δ)＞λ，即 x→。因此，是L的子代数。

“ ⇐ ”∀δ∈Ω ，假设存在 x0∈L ，使得 A(O,δ)＜A(x0,δ)，取 λ 满足 A(O,δ)＜ λ≤A(x0,δ)，则 A(x0,δ)≥ λ,A(O,δ)＜ λ ，所以。因为是L的子代数，所以，即 A(O,δ)≥λ，与 A(O,δ)＜λ矛盾。因此∀δ∈Ω ，∀x∈L ，A(O,δ)≥ A(x,δ)。

∀δ∈Ω，假设存在 x0,y0∈L ，使得 A(x0→y0,δ)＜A(x0,δ)∧A(y0,δ)，取 λ 满足 A(x0→y0,δ)＜ λ ≤A(x0,δ)∧A(y0,δ)，则 A(x0,δ)≥ λ,A(y0,δ)≥ λ ，A(x0→y0,δ)＜ λ ，从而。因为是 L 的子代数,，所以，与 x0→矛盾。因此 ∀δ∈Ω 及 ∀x,y∈L,A(x→y,δ)≥A(x,δ)∧ A(y,δ)。

综上所述,A是格蕴涵代数 L的Ω-模糊子代数。 □

类似于定理2的证明，可得定理3。

定理3设A:L×Ω→[0,1]是格蕴涵代数L的Ω-模糊集，A是格蕴涵代数L的Ω-模糊子代数⇔是 L的子代数，其中A(x,δ)＞ }λ,∀δ∈Ω 。

定理4是格蕴涵代数L的Ω-模糊子代数⇔是格蕴涵代数L的子代数。

证明“ ⇒ ”由于，故存在 x0∈S，即，由于是格蕴涵代数L的Ω-模糊子代数，故 ∀x∈L,∀δ∈Ω ，，取 x=x0，则

综上所述，S≠∅是格蕴涵代数L的子代数。

“ ⇐ ”∀δ∈Ω ，由于 S≠∅ 是 L的子代数，故0∈P，从 而，因 此 ∀x∈L,。假设存在 x0,y0∈S ，使得取因为是 S的 Ω-模糊特征函数，所以

推论1是格蕴涵代数L的Ω-模糊子代数是格蕴涵代数L的子代数。

定理5设 A:L×Ω→[0,1]是L的Ω-模糊集，A是L的Ω-模糊子代数⇔Aδ是L的模糊子代数，其中 Aδ:L→[0,1]:Aδ(x)=A(x,δ)，∀x∈L ，∀δ∈Ω 。

证明“⇒”若A是L的Ω-模糊子代数，则∀δ∈Ω，∀x,y∈L，一方面，Aδ(0)=A(0,δ)≥A(x,δ)=Aδ(x)；另一方面，Aδ(x→ y)=A(x→ y,δ)≥ A(x,δ)∧ A(y,δ)=Aδ(x)∧ Aδ(y)。

综上所述，Aδ是L的模糊子代数。

“ ⇐ ”若 Aδ是 L 的模糊子代数，则 ∀δ∈Ω,∀x,y∈L，由定义 8 可知，一方面，A(0,δ)=Aδ(0)≥ Aδ(x)=A(x,δ)；另一方面，A(x→y,δ)=Aδ(x→ y)≥Aδ(x)∧ Aδ(y)=A(x,δ)∧A(y,δ)。

综上所述，A是L的Ω-模糊子代数。 □

定理6设 A:L×Ω→[0,1]是L的Ω-模糊集，A是L的Ω-模糊子代数，则 Aσ是L的Ω-模糊子代数，其中

证明∀δ∈Ω ，∀x,y∈L ，一方面，由 Aσ(x,δ)的定义可知，另一方面，因为A是L的Ω-模糊子代数，所以

综上所述，Aσ是L的Ω-模糊子代数。 □

定理7若A、B是格蕴涵代数L的Ω-模糊子代数，则A⋂B是格蕴涵代数L的Ω-模糊子代数。

证明若A、B是格蕴涵代数L的Ω-模糊子代数，则∀δ∈Ω ，∀x,y∈L，一方面，

另一方面，

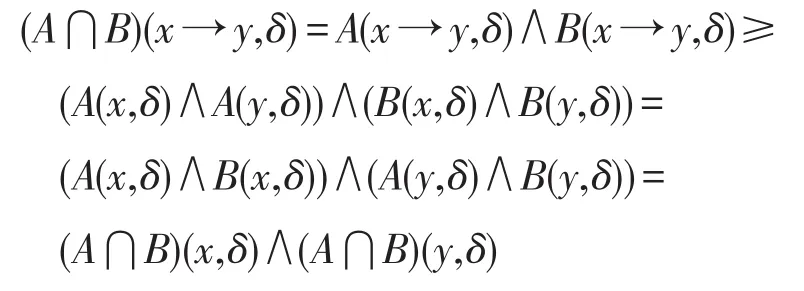
综上所述,A⋂B是格蕴涵代数L的Ω-模糊子代数。 □

推论2若Ai(i∈I)是格蕴涵代数L的Ω-模糊子代数，则⋂i∈IAi是格蕴涵代数L的Ω-模糊子代数。

引理6若Ai(i∈I)是格蕴涵代数L的Ω-模糊集，当 i≤j时,Ai⊆Aj,则 ∀x,y∈L,∀δ∈Ω,∨i∈I(Ai(x,δ)∧Ai(y,δ))=(∨i∈IAi(x,δ))∧(∨i∈IAi(y,δ))。

证明∀x,y∈L ，∀δ∈Ω ，显然 ∨i∈I(Ai(x,δ)∧Ai(y,δ))≤(∨i∈IAi(x,δ))∧(∨i∈IAi(y,δ))成立。若 ∨i∈I(Ai(x,δ)∧Ai(y,δ))≠(∨i∈IAi(x,δ))∧(∨i∈IAi(y,δ))，从而有 ∨i∈I(Ai(x,δ)∧ Ai(y,δ))＜(∨i∈IAi(x,δ))∧(∨i∈IAi(y,δ))，选 取 r 满 足∨i∈I(Ai(x,δ)∧ Ai(y,δ))＜ r＜(∨i∈IAi(x,δ))∧(∨i∈IAi(y,δ))。因为对于所有的 i,j∈I,Ai⊆Aj，或者 Ai⊇Aj，所以存在k∈I，使得 Ak(x,δ)∧Ak(y,δ)＞r；另一方面，对于所有的i∈I,Ai(x,δ)∧Ai(y,δ)＜r，矛盾。因此，∀x,y∈L，∀δ∈Ω，∨i∈I(Ai(x,δ)∧ Ai(y,δ))=(∨i∈IAi(x,δ))∧ (∨i∈IAi(y,δ))。 □

定理8设 Ai:L×Ω→[0,1](i∈I)是 L的 Ω-模糊集，若 Ai(i∈I)是L的Ω-模糊子代数，且当i≤j时，Ai⊆Aj，则 ⋃i∈IAi是 L 的 Ω-模糊子代数。

证明若 Ai(i∈I)是L的Ω-模糊子代数，则∀x,y,z∈L，∀δ∈Ω ，由定义8可知，一方面，

(⋃i∈IAi)(0,δ)= ∨i∈IAi(0,δ)≥ ∨i∈IAi(x,δ)=(⋃i∈IAi)(x,δ)另一方面，

综上所述，⋃i∈IAi是L的Ω-模糊子代数。 □

设A是X的一个Ω-模糊子集，0≤k≤1,∀x∈X,∀δ∈Ω ，定义 A∨k，A∧k如下：

定理9若A是格蕴涵代数L的Ω-模糊子代数，则A∧k是格蕴涵代数L的Ω-模糊子代数。

证明若A是格蕴涵代数L的Ω-模糊子代数，则∀δ∈Ω ，∀x,y∈L，一方面，

(A∧k)(O,δ)=A(O,δ)∧k≥A(x,δ)∧k=(A ∧ k)(x,δ)另一方面，

综上所述,A∧k是格蕴涵代数L的Ω-模糊子代数。 □

定理10若A是格蕴涵代数L的Ω-模糊子代数，则A∨k是格蕴涵代数L的Ω-模糊子代数。

证明若A是格蕴涵代数L的Ω-模糊子代数，则∀δ∈Ω ，∀x,y∈L，一方面，

另一方面，

综上所述,A∨k是格蕴涵代数L的Ω-模糊子代数。 □

定理11设L1、L2是格蕴涵代数，映射 f:L1→L2为格蕴涵满同态映射，若A是格蕴涵代数L1的Ω-模糊子代数，则 f(A)是格蕴涵代数L2的Ω-模糊子代数，其中 f(A)(y,δ)=sup{ |A(x,δ)f(x)=y,δ∈ Ω}。

证明∀y1,y2∈L2，因为映射 f:L1→L2为格蕴涵满同态映射，所以 ∃x1,x2∈L1，使得 f(x1)=y1，f(x2)=y2，且 f(O)=O，从而∀δ∈Ω，一方面，

综上所述,f(A)是格蕴涵代数L2的Ω-模糊子代数。 □

定理12设L1、L2是格蕴涵代数，映射 f:L1→L2为格蕴涵满同态映射，若B是格蕴涵代数L2的Ω-模糊子代数⇔ f-1(B)是格蕴涵代数L1的Ω-模糊子代数，其中 f-1(B)(y,δ)=B(f(y),δ),δ∈Ω 。

证明“⇒”若B是格蕴涵代数L2的Ω-模糊子代数，则 ∀y1,y2∈L1，∀δ∈Ω，一方面，f-1(B)(O,δ)=B(f(O),δ)≥ B(f(y1),δ)=f-1(B)(y1,δ)；另 一 方 面 ， f-1(B)(y1→ y2,δ)=B(f(y1→ y2),δ)=B(f(y1)→ f(y2),δ)≥ B(f(y1),δ)∧B(f(y2),δ)=f-1(B)(y1,δ)∧ f-1(B)(y2,δ)。

综上所述，f-1(B)是格蕴涵代数L1的Ω-模糊子代数。

“⇐”若 f-1(B)是格蕴涵代数L1的Ω-模糊子代数，∀y1,y2∈L2，因为 f:L1→L2为格蕴涵满同态映射，所以 ∃x1,x2∈L1，使得 f(x1)=y1，f(x2)=y2，且 f(O)=O，从而 ∀δ∈Ω，一方面，B(O,δ)=B(f(O),δ)=f-1(B)(O,δ)≥f-1(B)(x1,δ)=B(f(x1),δ)=B(y1,δ)；另一方面，B(y1→ y2,δ)=B(f(x1)→f(x2),δ)=B(f(x1→ x2),δ)=f-1(B)(x1→ x2,δ)≥f-1(B)(x1,δ)∧f-1(B)(x2,δ)。

综上所述,B是格蕴涵代数L2的Ω-模糊子代数。 □

设A、B分别是非空集合L1、L2的Ω-模糊子集，定义映射∀(x,y)∈L1×L2，∀δ∈Ω ，

则称 A×B为L1×L2的Ω-模糊子集，并称A×B为A、B关于Ω的直积。

定理13若 A、B分别是格蕴涵代数L1、L2的Ω-模糊子代数，则A×B是L1×L2的Ω-模糊子代数。

证明若A、B分别是格蕴涵代数L1、L2的Ω-模糊子代数，则一方面，∀(x,y)∈L1×L2，∀δ∈Ω ，

另一方面，∀(x1,y1),(x2,y2)∈L1×L2，∀δ∈Ω ，

综上所述，A×B是L1×L2的Ω-模糊子代数。□

定义9设A×B是非空集合L1×L2的Ω-模糊子集，则定义L1的Ω-模糊子集：

A1(x,δ)= ∨z∈L2(A × B)((x,z),δ)

定义L2的Ω-模糊子集：

定理14若A×B是L1×L2的Ω-模糊子代数，则A1(x,δ)是 L1的 Ω-模糊子代数，B1(y,δ)是 L2的 Ω-模糊子代数。

证明若A×B是L1×L2的Ω-模糊子代数，则一方面，∀(x,y)∈L1×L2，∀δ∈Ω ，

由z的任意性可知：

另一方面，

由z1的任意性知：

再由z2的任意性知：

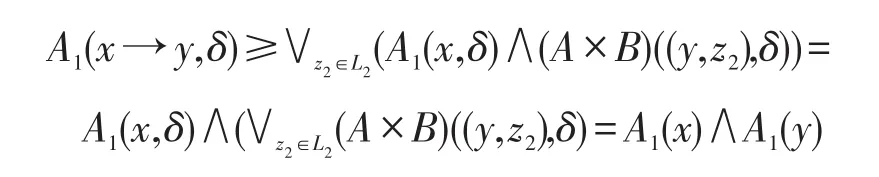
综上所述，A1(x,δ)是L1的Ω-模糊子代数。

同理可证B1(y,δ)是L2的Ω-模糊子代数。 □

4 结束语

本文将Ω-模糊集的思想与方法应用于格蕴涵代数，引入了Ω-模糊子代数的概念，并讨论了它的性质及其与格蕴涵代数子代数间的相互关系，获得了若干有意义的结果。这些结论有助于进一步认识格蕴涵代数，促进了格蕴涵代数的发展；此外，还可以用类似的方法研究格蕴涵代数的其他子结构，将在后续工作中进行讨论。

[1]Zadeh LA.Fuzzy sets[J].Information and Control,1965,8(3):338-353．

[2]Rosenfeld A.Fuzzy groups[J].JournalofMathematicalAnalysisand Applications,1971,35(3):512-517.

[3]Zadeh L A.The concept of a linguistic variable and its application to approximate reasoning[J].Information Science,1975,8(3):199-249.

[4]Pu Paom ing,Liu Yingming.Fuzzy topology(I)neighborhood structure of a fuzzy pointand Moore-Sm ith convergence[J].Journal of Mathematical Analysis and Applications,1980,76(2):571-599．

[5]Pu Paoming,Liu Yingming.Fuzzy topology(II)product and quotient spaces[J].Journal of Mathematical Analysis and Applications,1980,77(1):20-37．

[6]Bhakat SK,Das P.On the definition of a fuzzy subgroup[J].Fuzzy Sets Systems,1992,51(2):235-241．

[7]Bhakat SK,Das P.Fuzzy subgroups[J].Fuzzy Sets Systems,1996,80(3):359-368.

[8]Bhakat SK,Das P.Fuzzy subrings and ideals redefined[J].Fuzzy Sets Systems,1996,81(3):383-393.

[9]Liao Zuhua,Gu Hui.(∈ ,∈ ∨q(λ,μ))-fuzzy normal subgroup fuzzy normal subgroup[J].Fuzzy Systems and Mathematics,2006,20(5):38-43.

[10]Zhang Jianzhong,Fu Xiaobo,Liao Zuhua.(∈,∈ ∨q(λ,μ))-fuzzy ideal of N(2,2,0)algebra[J].Journal of Frontiers of Computer Science and Technology,2013,7(11):1048-1056.

[11]Fan Xiaowei,Liao Zuhua,Fan Yingying,etal.(∈,∈ ∨q(λ,μ))-fuzzy Г-completely prime ideals ofГ-semigroups[J].Fuzzy Systemsand Mathematics,2014,28(2):52-61．

[12]Young B J,Kyung H K.OnΩ-fuzzy ideals of BCK/BCI-algebras[J].The Journal of Fuzzy Mathematics,2001,9(1):173-180.

[13]Peng Jiayin.Ω-fuzzy p-ideals of BCI-algebras[J].Journal of Neijiang NormalUniversity,2008,23(12):8-15.

[14]Peng Jiayin.Ω-fuzzy H-ideals of BCI-algebras[J].Journal of Neijiang NormalUniversity,2009,24(2):5-10.

[15]Peng Jiayin.Ω-fuzzy dot ideals of BCH-algebras[J].Fuzzy Systemsand Mathematics,2009,23(6):5-11.

[16]Peng Jiayin.Ω-fuzzy positive implicative ideals in BCK-algebras[J].Mathematics in Practice and Theory,2010,40(2):157-163.

[17]Zhu Xiaoying,Liao Zuhua,Luo Xiaotang,et al.Ω-fuzzy subsemigroup of sem igroups[J].Journal of Jiangnan University:Natural Science Edition,2013,12(3):343-346.

[18]Luo Xiaotang,Liao Zuhua,Zhu Xiaoying,et al.GeneralizedΩ-fuzzy bi-ideals of sem igroups[J].Journal of Jiangnan University:NaturalScience Edition,2013,12(4):480-484.

[19]Luo Xiaotang,Liao Zuhua,Zhu Xiaoying,etal.Ω-fuzzy interior ideals of sem igroups[J].Journalof Jiangnan University:NaturalScience Edition,2014,12(4):400-494.

[20]Zhu Chan,Liao Zuhua,Luo Xiaotang,et al.Ω-fuzzy complemented subsemiring[J].Fuzzy Systems and Mathematics,2014,28(5):11-18.

[21]Liu Weifeng.Ω-fuzzy subalgebra of boolean algebra[J].Journal of Hubei University:Natural Science,2013,35(2):144-148.

[22]Tang Huajing,Zhang Hui.Ω-fuzzy soft rings[J].Computer Engineering and Applications,2015,51(9):122-124.

[23]Wu Wangming.Fuzzy implication algebras[J].Fuzzy Systems and Mathematics,1990,4(1):56-64.

[24]Xu Yang.Lattice implication algebras[J].Journal of Southwest Jiaotong University,1993,28(1):20-27.

[25]Xu Yang,Ruan Da,Qin Keyun.Lattice-valued logic[M].Berlin:Springer,2003.

[26]Liu Yi,Xu Yang,Qin Ya.Interval-valued(α,β)-fuzzy lattice implication subalgebras[J].Computer Science,2011,38(4):263-266.

[27]Qin Xuecheng,Liu Chunhui.Interval-valued fuzzy subalgebras of lattice implication algebras[J].Pure and Applied Mathematics,2011,27(6):801-807.

[28]Liu Chunhui.On IV-(∈,∈∨q)-fuzzy lattice implication subalgebras[J].Computer Engineering and Applications,2012,48(26):39-43.

[29]Fu Xiaobo,Liao Zuhua,Zheng Gaoping.(∈,∈ ∨q(λ,μ))-fuzzy subalgebra of lattice implication algebras[J].Fuzzy Systems and Mathematics,2014,28(6):44-52.

附中文参考文献：

[10]张建忠,傅小波,廖祖华.N(2,2,0)代数的 (∈,∈∨q(λ,μ))-理想[J].计算机科学与探索,2013,7(11):1048-1056.

[11]范晓威,廖祖华,范莹莹,等. Γ-半群的 (∈,∈ ∨q(λ,μ))-模糊Γ-完全素理想[J].模糊系统与数学,2014,28(2):52-61.

[15]彭家寅.BCH-代数的Ω-模糊点理想[J].模糊系统与数学,2009,23(6):5-11.

[16]彭家寅.BCH-代数的Ω-模糊正定关联理想[J].数学的实践与认识,2010,40(2):157-163.

[17]朱晓英,廖祖华,罗晓棠,等.半群的Ω-模糊子半群[J].江南大学学报:自然科学版,2013,12(3):343-346.

[18]罗晓棠,廖祖华,朱晓英,等.半群的广义Ω-模糊双理想[J].江南大学学报:自然科学版,2013,12(4):480-484.

[19]罗晓棠,廖祖华,朱晓英,等.半群的Ω-模糊内理想[J].江南大学学报:自然科学版,2014,12(4):400-494.

[20]朱婵,廖祖华,罗晓棠,等.Ω-模糊可补子半环[J].模糊系统与数学,2014,28(5):11-18.

[21]汤华晶,张慧.Ω-模糊软环[J].计算机工程与应用,2015,51(9):122-124.

[22]刘卫锋.布尔代数的Ω-模糊子代数[J].湖北大学学报:自然科学版,2013,35(2):144-148.

[23]吴望名.Fuzzy蕴涵代数[J].模糊系统与数学,1990,4(1):56-64．

[24]徐扬.格蕴涵代数[J].西南交通大学学报,1993,28(1):20-27.

[26]刘熠,徐扬,秦亚.区间值(α,β)-模糊格蕴涵子代数[J].计算机科学,2011,38(4):263-266.

[27]秦学成,刘春辉.格蕴涵代数的区间值模糊子代数[J].纯粹数学与应用数学,2011,27(6):801-807.

[28]刘春辉.关于IV-(∈,∈∨q)模糊格蕴涵子代数[J].计算机工程与应用,2012,48(26):39-43.

[29]傅小波,廖祖华,郑高平,等.格蕴涵代数 (∈,∈∨q(λ,μ))-模糊子代数[J].模糊系统与数学,2014,28(6):44-52.

FU Xiaobo was born in 1980.He is a lecturer atWuxi Institute of Technology,and themember of CCF.His research interests include artificial intelligence and granular computing,etc.

傅小波（1980—），男，江苏灌云人，无锡职业技术学院讲师，CCF会员，主要研究领域为人工智能，粒计算等。

LIAO Zuhuawasborn in 1957.He isa professor and M.S.supervisor at Jiangnan University.His research interests include artificial intelligence and granular computing,etc.

廖祖华（1957—），男，江西奉新人，江南大学教授、硕士生导师，主要研究领域为人工智能，粒计算等。发表学术论文100多篇。

Ω-Fuzzy Subalgebra in Lattice Im plication Algebra*

FU Xiaobo1,LIAO Zuhua2+
1.Wuxi Instituteof Technology,Wuxi,Jiangsu 214121,China
2.Schoolof Science,Jiangnan University,Wuxi,Jiangsu 214122,China

LetΩbe a set.By combining theΩ-fuzzy setsand the lattice implication algebras,this paper introduces the concepts ofΩ-fuzzy subalgebra in the lattice implication algebra,and investigates some related properties.Beside,this paper obtains some equivalent descriptions of theΩ-fuzzy subalgebra in the lattice implication algebra,and gives the relationsbetweenΩ-fuzzy subalgebra and the subalgebra in the lattice implication algebra.Then this paper studies some basic properties of theΩ-fuzzy subalgebra under the intersection,union and other operationsof Ω-fuzzy sets,and discusses some basic propertiesof homomorphic image and homomorphic preimage ofΩ-fuzzy subalgebra.Finally,thispaperstudies theΩ-fuzzy subalgebra directproduct in the lattice implication algebra.

lattice implication algebra;Ω-fuzzy subalgebra;homomorphic;directproduct

2016-04,Accepted 2016-06.

A

：TP18

*The National Natural Science Foundation of China under Grant Nos.611702121,11401259(国家自然科学基金);the Natural Science Foundation of Jiangsu ProvinceunderGrantNo.BK2015117(江苏省自然科学基金).

CNKI网络优先出版:2016-06-27,http://www.cnki.net/kcms/detail/11.5602.TP.20160627.0929.004.htm l