基于广义均值的鲁棒典型相关分析算法*
顾高升,葛洪伟,2+,周梦璇
1.江南大学 物联网工程学院,江苏 无锡 214122
2.江南大学 轻工过程先进控制教育部重点实验室,江苏 无锡 214122
基于广义均值的鲁棒典型相关分析算法*
顾高升1,葛洪伟1,2+,周梦璇1
1.江南大学 物联网工程学院,江苏 无锡 214122
2.江南大学 轻工过程先进控制教育部重点实验室,江苏 无锡 214122
+Corresponding autho author:r:E-mail:ghw8601@163.com
GU Gaosheng,GE Hongwei,ZHOU Mengxuan.Robust canonical correlation analysis based on generalized mean.Journalof Frontiersof Computer Science and Technology,2017,11(7):1140-1149.
广义均值;均方误差;典型相关分析;鲁棒性;鲁棒典型相关分析
1 引言
典型相关分析(canonical correlation analysis,CCA)[1]是一种研究同一对象两组变量之间相关性的多元统计方法,可用于数据的特征抽取、降维和可视化。与单模态的主成分分析(principal component analysis,PCA)[2]不同,CCA更适用于多模态数据[3]的特征抽取与融合。CCA通过最大化不同模态间的相关性,消除数据间的冗余信息,提取重要特征,强化后续学习(如分类)任务的性能。近年来,CCA及其衍生模型成功应用于人脸识别、气象分析、生物信息融合和社会科学等领域。但CCA本质上是一种线性子空间的学习方法,其学习到的是一种全局线性情况下的线性特征。对于非线性的场景,CCA学习往往导致欠学习的结果。为此,Akaho[4]结合核技术提出了核CCA(kernel CCA,KCCA),克服了CCA在非线性情况下的不足。2000年,Roweis等人[5]提出了局部线性嵌入(local linear embedding,LLE)的非线性降维方法,流形学习(manifold learning,ML)从此得到深入的研究。Sun等人[6]引入流形学习中局部保持投影(locality preserving projection,LPP)[7]的思想,保留数据中的流形结构信息,提出了一种局部保持的CCA(locality preserving CCA,LPCCA),大大拓展了CCA在非线性情况下的应用。尽管如此,CCA、KCCA和LPCCA都是基于欧氏距离的方法,从多元线性回归分析的角度看,它们的目标优化函数都是基于L2范数的最小均方误差(mean square error,MSE),并且算法都未考虑样本集中的野值点对目标优化函数的影响。然而,在现实场景中,野值点普遍存在于观测的数据集中。研究表明[8],采用L2范数的MSE的欧式距离方法对于野值点都存在着非鲁棒性。因此,文献[9]利用核诱导距离替换基于L2范数的欧式距离,提出基于核诱导的CCA(CCA based on kernelinducedmeasure,KI-CCA)。KI-CCA用核诱导距离代替原始的欧式距离,减小了MSE中野值点的权重,达到抑制野值点的作用,增强算法的鲁棒性。但与CCA、KCCA和LPCCA类似,KI-CCA最终转化为广义特征值求解,在高维小样本[10-11]情况下,其样本协方差矩阵极可能奇异,这对算法的鲁棒性带来影响。为克服高维小样本问题,样本一般要进行预处理,即利用PCA提取主要信息,降低维度,以达到样本协方差矩阵可逆的目的,但PCA不能确保提取出充足的信息,因此PCA+CCA并不能保证算法的有效性。为了既解决高维小样本问题,又能使算法给出完整的特征信息,文献[10]提出了一种完备的CCA(complete CCA,C3A)。实验结果[10]显示,C3A能够完整地保留CCA的相关信息和投影方向,提高算法的稳定性。另外,An等人[11]的鲁棒CCA(robustCCA,ROCCA)用可行的近似矩阵替换原来奇异的样本协方差矩阵来解决高维小样本问题,在身份识别实验[11]中取得良好的效果。然而,C3A和ROCCA解决了高维小样本导致样本协方差矩阵奇异的问题,却未考虑样本中野值点对算法鲁棒性的影响。
广义均值(generalizedmean,GM)[12]是算术平均值的推广形式。通过调节GM的p值可以表现出多种数据的中心。文献[13]结合广义均值提出了一种新颖的有偏鉴别分析(biased discrim inantanalysis usinggeneralized mean,BDAGM),增强正向样本的作用,抑制野值点的干扰。人脸实验证明[13],GM增强了算法的鲁棒性,算法性能得到了提升。
为克服CCA的非鲁棒性,提高算法的性能,本文将GM引进CCA中,修改传统CCA准则函数的MSE,提出一种新的具有鲁棒性的CCA(CCA based on generalizedmean,GMCCA)。GMCCA具有如下的优点:
(1)通过广义均值抑制野值点对准则函数的影响;
(2)通过迭代求解的方法避免了高维小样本问题导致样本协方差矩阵奇异的问题,而且具有较快的收敛速度。
2 典型相关分析
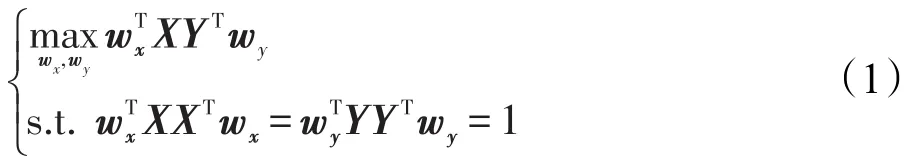
其中,X=(x1,x2,…,xN),Y=(y1,y2,…,yN);(·)T表示向量或者矩阵的转置,下同。从多元线性回归的角度分析,式(1)可以转化为下面的极小值优化问题[14]:

根据文献[15],CCA的求解一般可以转化为对应的广义特征值问题,如下所示:

令 Sxx=XXT,Syy=YYT,Sxy=XYT,Syx=YXT。式(3)可以表示成如下的两个广义特征值问题:

并且wx和wy具有如下的等式关系:

最后选取最大的前d个特征值所对应的特征向量组合成两组投影集

3 广义均值
假设 p≠0,对于一个标量数据集{ai>0,i=1,2,…,N}的广义均值MG[12]定义如下:

可以看出算术平均值、几何平均值和调和平均值是广义平均值分别取p=1,p→0,p=-1时的特例。而且数据集{ai}中的最大值和最小值分别在p→+∞和p→-∞时获得。可以注意到,随着 p增大(减小),数据集{ai}中的较小(较大)数对广义均值MG的作用越大。由此,可以通过控制p值来调整数据集{ai}中各数对MG的影响。受此启发,可以用广义均值的这种特性来控制野值点对结果的影响。
进一步分析,文献[14]指出,广义均值MG中的可以由数据集{ai}的一组非负的线性组合表示:

bi可以看成ai的权重,即ai对GM的贡献值。当p<1时,随着 ai越大,bi越小,意味着当 p<1时,广义均值MG受{ai}中较小值的影响较大,并且p越小,影响越大。广义均值的这种性质在GMCCA抑制野值点的影响中起到主要作用。
4 基于广义均值的典型相关分析

对于一组已中心化的样本集
相对于正向样本,野值点的e(Wx,Wy)较大。因此,为得到鲁棒性的效果,野值点e(Wx,Wy)对准则函数的影响应尽量小,而突出正向样本的相关误差所带来的影响。从多元线性回归的角度,根据广义均值的思想,本文提出如下GMCCA的准则函数JG(Wx,Wy):

根据式(6)中 p值的讨论,当 p<1时,可抑制野值点对JG(Wx,Wy)的影响。因此,本文只考虑 p<1的情况。根据式(7),GMCCA的投影集Wx和Wy可通过如下的极小值优化问题求得:


其中,|·|是绝对值函数,保证αi的非负性。由此可以看出GMCCA鲁棒性的本质:当 p<1时,αi的值随相对误差增大而减小,因此对于投影空间中相关误差较大的样本点,即野值点,赋予了较小的权重,抑制野值点对准则函数的不良影响,增强算法的鲁棒性。
绝对值函数导致式(9)不能通过普通的求导方法求解Wx和Wy。本文采用一种线性迭代方法求解式(9)。假设第t次迭代得到的Wx和Wy分别为和,首先固定可以通过如下的极小值问题求得:
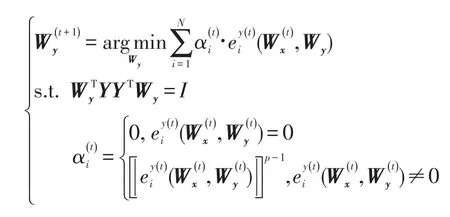
对上式的具体求解如下:

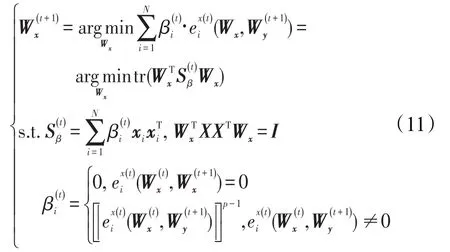
从上述的分析来看,GMCCA不同于传统的CCA,其求解的两组特征投影集是分开获得的,Wx和Wy并无CCA中的等式关系。Wx和Wy分别是样本集X和Y的加权协方差最大的d个特征值对应的正交特征向量集。而且整个求解过程并不涉及对样本集X和Y的协方差矩阵的求逆。因此,GMCCA避免了在传统CCA中高维小样本引起样本协方差矩阵奇异的问题。
因为Wx和Wy的初始值会影响迭代的次数和结果,所以本文选取传统CCA训练出来的和初始化Wx和Wy。本文的实验显示,和初始化的Wx和Wy能使算法获得良好的结果。GMCCA算法具体如下:
1.t=0,
2.Whilet<T
3.根据式(10),迭代t1次求得稳定的
4.根据式(11),迭代t2次求得稳定的
5.t←t+1
6.End
5 实验结果与分析
为验证GMCCA的有效性,本文在多特征手写体数据库(multiple feature database,MFD,http://archive.ics.uci.edu/m l/datasets/Multiple+Features)、人脸数据库(ORL,http://www.cl.cam.ac.uk/research/dtg/attarchive/facedatabase.htm l)和对象特征数据库(COIL-20,http://www.cs.columbia.edu/CAVE/software/softlib/coil-20.php)3个真实数据集上进行实验,并与PCA、CCA、ROCCA、C3A和KI-CCA进行对比。ROCCA通过构建近似矩阵代替样本协方差矩阵,消除高维小样本问题,通过身份识别[13]的实验验证了ROCCA的有效性。C3A克服了PCA+CCA可能丢失信息的问题,提取出更加完备的典型相关特征。ROCCA用核诱导距离代替传统CCA的欧氏距离,提高了算法鲁棒性。
在本文所有实验中,GMCCA的p设置为0.1,t1、t2和T分别设置为10、10和20。PCA需要将两组特征首尾相连以形成新的高维特征向量,然后用PCA进行特征提取,CCA、ROCCA、C3A、KI-CCA和GMCCA提取特征后通过串联的方式,即将两组降维后的特征首尾相连地串接在一起进行识别分析。分类器采用最近邻分类器。本文采用测试样本的分类识别率来评价算法的性能。识别率在0~100%之间,识别率越高,该算法较其他算法越优秀;识别率越稳定,该算法较其他算法性能越好。
5.1 多特征手写体实验
本实验用多特征手写体数据库测试GMCCA的性能。该数据库包含0~9共10个数字的6个特征数据集,每类200个样本,共2 000个样本。从二值化手写体数字图像中抽取6个特征,包括傅里叶系数、轮廓相关特征、Karhunen-Loève展开特征、像素平均、Zernike矩和形态学特征,其对应的特征名称和维数分别为(fou,76)、(fac,216)、(kar,64)、(pix,240)、(zer,47)和(mor,6)。在此数据库上,任选2组特征作为输入,共有15种组合方式。对于每个特征组合,从每类中随机选取100个样本用于训练,剩下的100个样本用于测试。
表1所示为6种算法在不同特征组合上的10次随机实验的平均识别结果,每种算法中的最佳识别率用黑体表示,下同。此实验中,训练样本每类都包含100个训练样本,说明样本采集充足,样本包含野值点的可能性也将增大。因此,GMCCA能比PCA、CCA、ROCCA和C3A提取出更加鲁棒的特征,而KICCA的核诱导距离采用的是高斯核,对于15种特征组合并不一定都适应,且KI-CCA计算时采用了泰勒展开式近似,丢失了一部分信息,这些不足之处将会导致KI-CCA算法的不稳定性。表1的结果验证了上述的推论,在绝大多数的组合中GMCCA算法的平均识别率优于其他算法,且明显高于CCA的识别效果。此外,15种组合的平均识别率也高于其他算法。这些结果验证了GMCCA的有效性。在fou-pix、kar-pix、mor-pix和mor-zer组合中,GMCCA的识别率略低于其他某一算法,虽然GMCCA的识别率仍高于CCA,但也表示GMCCA在一些特征组合中仍有不足之处。

Table1 Recognition ratesof6 algorithmson MFD database表1 6种算法在M FD数据库上的识别结果
5.2 ORL人脸数据库
为了进一步验证GMCCA的有效性,本实验选取人脸姿态变化较大的ORL数据库,其包含40名志愿者的人脸图像,每人10幅图像,分别拍摄于不同时间和光照条件下,具有不同表情和面部细节,其深度旋转和平面旋转可达到20°,人脸的尺度也多达10°的变化。图1显示了该人脸数据库中一个人的6幅图像。

Fig.1 6 picturesofone person on ORL database图1 ORL人脸数据库中一个人的6幅图像
实验从每个人的10幅图像中随机选取4、5、6、7或8幅图像用于训练,其余用于测试;对每幅图像抽取3组特征。其中,将原始图像特征记为O;将原始图像用局部二值模式(localbinary pattern,LBP)[16]提取后的特征记为L;将原始图像用方向梯度直方图(histogram of oriented gradient,HOG)[17]提取后的特征记为H。LBP和HOG特征及其组合特征在人脸识别问题上已被证明是有效的[18]。为尽量避免奇异性问题,用PCA将上述3种特征约减至100维。
表2所示为6种算法在3种特征组合上的10次随机实验的平均识别结果,“n”表示每类的训练样本数,下同。ORL数据库每类只包含10个样本,因此此数据库上的实验极易导致奇异性问题。而且从图1中可以看出,每类中的面部旋转尺度不大,图像较为清晰,所带来的噪声信息较少,因此处理样本协方差的奇异性的能力决定了算法的主要性能。从表2中可以看出,解决高维小样本问题的ROCCA、C3A和GMCCA明显比PCA、CCA和KI-CCA的识别率高。另外,GMCCA求解的是样本的加权协方差矩阵,比ROCCA和C3A求解的近似协方差矩阵和组合协方差矩阵更能保留样本视图之间的相关性,即相关性越强,对应的相关误差越小,权重越大。因此,GMCCA提取的特征更加具有鲁棒性。表2的结果显示,在绝大数的情况下,GMCCA的识别效果在3种不同组合下均优于其他5种算法,并且比较所有组合的平均识别率,GMCCA也优于其他5种算法。从表2中还可以看出,GMCCA的识别效果比传统的CCA有较大提高,尤其当训练样本数较少时,如每类4个训练样本。这些结果表明GMCCA提取的特征更具有鲁棒性,验证了方法的有效性。表2中的结果也显示,有4种情况,GMCCA的识别率略低于其他算法,但与最优值十分接近。
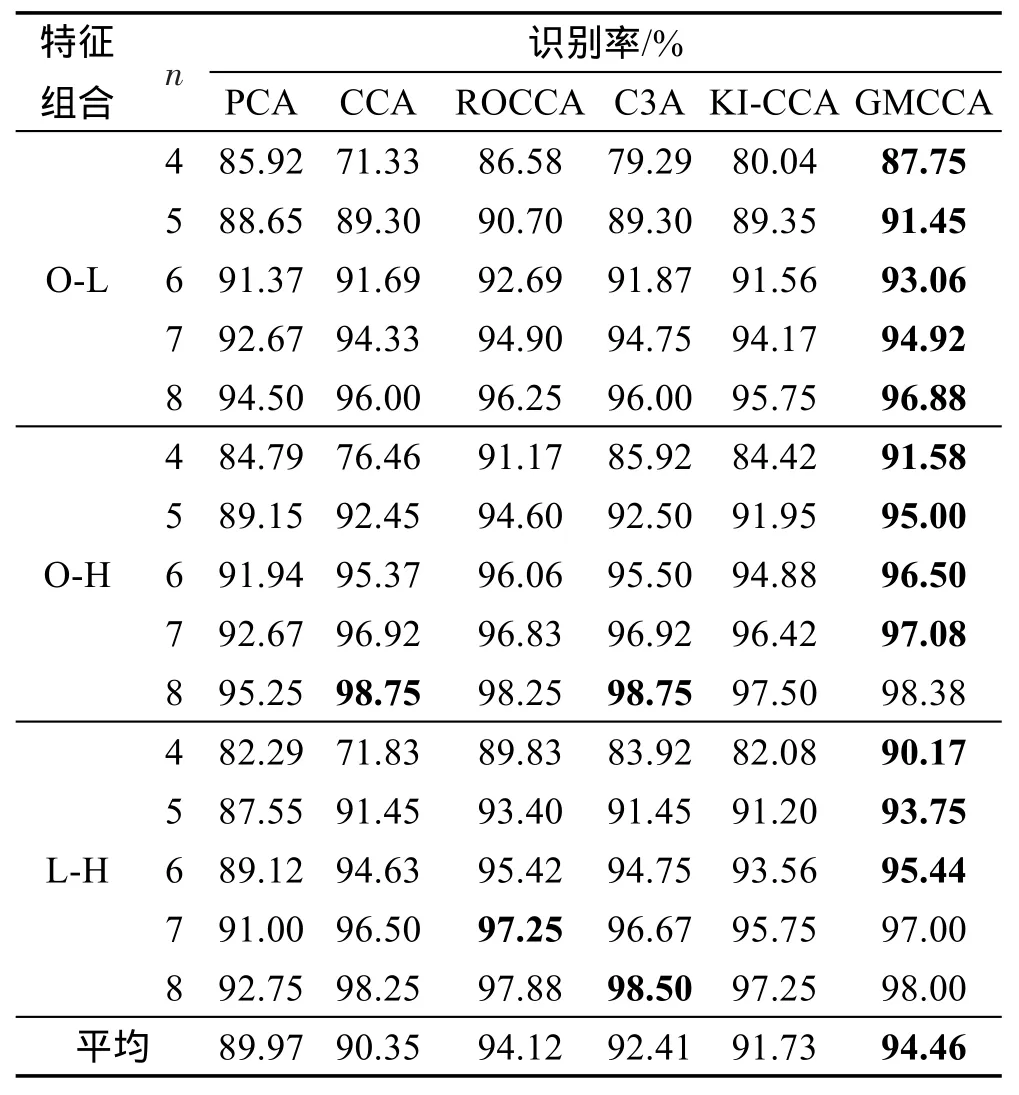
Table2 Recognition ratesof 6 algorithmson ORL database表2 6种算法在ORL人脸数据库上的识别结果
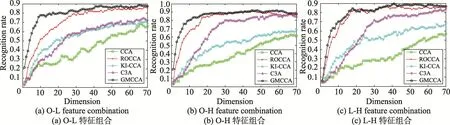
Fig.2 Recognition ratesof 5 canonical correlation algorithmsw ith changed dimensionson ORL database图2 5种典型相关算法在ORL数据库上随维数变化的识别结果
再次选取ORL数据库中每人的前4幅图像进行训练,剩余图像用于测试。因为在表2中其他5种算法明显优于PCA,所以图2显示了5种典型相关算法在3种特征组合下随维度变化的识别结果。正是由于GMCCA通过求解加权的样本协方差矩阵,既避免了高维小样本导致的样本协方差矩阵奇异的问题,又能保持样本视图之间的相关性。从图2可以看出,GMCCA优于其他4种算法,尤其在维数较少的情况下,GMCCA的识别率明显高于其他算法。从算法的稳定性角度,GMCCA也比其他4种算法要好。实验结果再次有效地验证了GMCCA的鲁棒性。
5.3 COIL-20对象数据库
COIL-20数据库包含了20个对象的1 440幅灰度图像,分别对每个对象从0°~360°进行水平方向的旋转,每5°采样一幅图像,每个对象共计采集72幅图像。图3显示了数据库中的20个对象,它们具有复杂的几何特征。

Fig.3 20 objectpictures in COIL-20 database图3 COIL-20中20个对象图像
实验中,从每个对象的72幅图像中随机选取10、20、30、40和50幅图像,剩下的图像用于测试。独立进行10次随机实验,然后计算其平均识别率。实验中对每幅图像提取3组特征。本次实验仍将原始图像特征记为O;原始图像用LBP提取后的特征记为L;将原始图像用HOG提取后的特征记为H。执行PCA将上述3种特征约减至50维。
表3显示了6种算法在3种特征组合上的10次随机实验的平均识别结果。从表3的实验结果可以看出,GMCCA明显优于传统的CCA。因为GMCCA不仅考虑到奇异性,而且通过广义均值抑制了野值点对准则函数的影响,提取出更加鲁棒的特征,所以表3显示在绝大部分情况下,GMCCA比ROCCA、C3A和KI-CCA效果好。而且在每类训练样本较少的情况下,如10、20时,GMCCA的识别率明显优于其他算法。注意到表3中,CCA和C3A的识别率相当,说明此数据集在PCA提取特征降维后,CCA能够提取出完备的特征信息,而GMCCA的识别率优于CCA和C3A,也说明GMCCA不仅提取出完备的特征信息,而且提取出的特征更加具有鲁棒性。在表3中仍有两种情况下,GMCCA的识别率比其他算法略低,但差异很小。并且从整体平均识别率来看,GMCCA优于其他5种算法。这些实验结果验证了GMCCA的有效性和鲁棒性。
再次选取COIL-20数据库中每个对象的前25幅图像进行训练,剩余图像用于测试,图4显示了5种算法在3种特征组合下随维度变化的识别结果。从图4中可以看出,GMCCA明显优于其他4种算法。GMCCA相比传统的CCA,抑制了野值点的影响,识别率有了较大的提高。而且GMCCA基于广义均值的MSE比KI-CCA基于核诱导的MSE更加具有鲁棒性,识别率更高。从图4中还可以看出,随维数的增加,GMCCA的识别率比用于解决高维小样本问题的ROCCA和C3A更高,更加稳定,这是由于GMCCA既抑制了野值点的影响,又充分保留了样本视图之间的相关性。图4的结果也进一步验证了图2中得出的GMCCA在维数较少时识别率比其他算法更高的结论。这些结果说明GMCCA提取的特征更加具有鲁棒性。注意到,CCA和C3A的Dimension-Recognition Rate折线是重合的,验证了表3中CCA和C3A的识别率相当的结论,说明CCA可以从数据集中提取出完备的特征信息。这也侧面反映了在CCA能够提取完备信息的同时,GMCCA能抑制野值点的影响,提取出更加鲁棒的特征。上述的实验结果进一步验证了GMCCA的有效性和鲁棒性。

Table3 Recognition ratesof6 algorithmson COIL-20 database表3 6种算法在COIL-20数据库上的识别结果
5.4GMCCA的收敛性
GMCCA是通过线性迭代的方法获得两组稳定的投影集Wx和Wy。为检验GMCCA的收敛性,本节以ORL人脸数据库中的O-L特征组合为代表进行实验。从每类样本中选取4幅图像用于训练,其余的图像用于测试,独立进行100次实验,取平均结果进行分析。本节定义两个矩阵A∈ℜm×n和B∈ℜm×n之间的均方误差MSE(A,B):

那么,Wx和Wy迭代第t次与第t-1次的迭代均方误差分别为:

图5显示了前100次迭代Wx和Wy的平均迭代均方误差图。从图5(a)中可以看出,Wx的100次平均迭代均方误差在前10次迭代中能够很快地降低,并且在第10次迭代之后,迭代均方误差稳定在一个很小的值2.226×10-8左右,此时能够认为Wx已经收敛。从图5(b)中可以看出,Wy的100次平均迭代均方误差与Wx有类似的结果,迭代均方误差在前10次迭代中能够很快地降低,并且在第10次迭代之后,迭代均方误差稳定在一个很小的值1.483×10-9左右,此时能够认为Wy已经收敛。综上所述,GMCCA是收敛的算法,且具有很快的收敛速度,即Wx和Wy能够在10次迭代后即可认为已经收敛。

Fig.4 Recognition ratesof5 canonical correlation algorithmsw ith changed dimensionson COIL-20 database图4 5种典型相关算法在COIL-20数据库上随维数变化的识别结果

Fig.5 Average iterativeMSE ofGMCCAw ith changed iterationsunderO-L feature combination图5 GMCCA在O-L特征组合下平均迭代M SE随迭代次数的变化
图6显示了在100次独立实验下,GMCCA的平均识别率随迭代次数变化的图像。从图6的结果中可以看出,GMCCA的识别率在前10次迭代中得到快速提高,在10次迭代之后,识别率趋于稳定的结果87.92%。此实验结果进一步佐证了图5的实验分析,验证了上述GMCCA的Wx和Wy在10次迭代之后达到收敛要求,算法可以认为已经收敛的结论。综上所述,GMCCA是一种收敛的算法,并且具有较快的收敛速度,在10次迭代之后即可收敛,算法的识别率也随着Wx和Wy的收敛趋于稳定。上述的实验结果也验证了GMCCA的有效性。
6 结束语
本文在传统CCA的基础上基于广义均值提出了鲁棒典型相关分析GMCCA。从多元线性回归分析的角度,GMCCA利用广义均值修改了传统的MSE,通过广义均值调整野值点对准则函数的权重,克服了CCA对野值点非鲁棒性的限制。并且GMCCA彻底解决了高维小样本问题,提高了相关分析的性能。在MFD、ORL和COIL-20数据库上的实验结果也验证了GMCCA的有效性。但实验结果也显示GMCCA仍有不足之处。下一步,将考虑把核技术引进GMCCA,解决非线性问题,提高算法的性能,并将GMCCA推广至3个或更多视图的学习中,实现多视图下的非线性的鲁棒信息融合。
[1]Hotelling H.Relationsbetween two setsof variates[J].Biometrika,1936,28(3/4):321-377.
[2]Jolliffe IT.Principal componentsanalysis[M].New York:Springer-Verlag,1986.
[3]Xu Yumeng,Wang Changdong,Lai Jianhuang.Weighted multi-view clusteringw ith feature selection[J].Pattern Recognition,2016,53:25-35.
[4]Akaho S.A kernelmethod for canonical correlation analysis[C]//Proceedings of the 2001 International Meeting of Psychometric Society,Osaka,Japan,Jul15-19,2001.
[5]Roweis S T,Saul L K.Nonlinear dimensionality reduction by locally linear embedding[J].Science,2000,290(5500):2323-2326.
[6]Sun Tingkai,Chen Songcan.Locality preserving CCA w ith applications to data visualization and pose estimation[J].Image Vision Computing,2007,25(5):531-543.
[7]He Xiaofei,Niyogi P.Locality preserving projections[C]//Advances in Neural Information Processing Systems 16,Vancouver,Canada,Dec 8-13,2003.Cambridge:M IT Press,2003:153-160.
[8]He Ran,Hu Baogang,ZhengWeishi,etal.Robustprincipal component analysis based onmaximum correntropy criterion[J].IEEE Transactions on Image Processing,2011,20(6):1485-1494.
[9]Ding Xin,Chen Xiaohong,Chen Songcan.Robust canonical correlation analysis based on kernel-induced measure[J].Journal of Frontiers of Computer Science and Technology,2012,6(8):708-716.
[10]Xing Xianglei,Wang Kejun,Yan Tao,etal.Complete canonical correlation analysis w ith application to multi-view gait recognition[J].Pattern Recognition,2016,50(C):107-117.
[11]An Le,Yang Songfan,Bhanu B.Person re-identification by robust canonical correlation analysis[J].IEEE Singal Processing Letters,2015,22(8):1103-1107.
[12]Bullen P.Handbook of means and their inequalities[M].Berlin:Springer,2003.
[13]Oh J,Kwak N,Lee M,et al.Generalized mean for feature extraction in one-class classification problems[J].Pattern Recognition,2013,46(12):3328-3340.
[14]Hoegaerts L,Suykens JA K,Vandewalle J.Subset based least squares subspace regression in RKHS[J].Neurocomputing,2005,63:293-323.
[15]Chen Songcan,Zhang Daoqiang.Robust image segmentation using FCM w ith spatial constraintsbased on new kernelinduced distance measure[J].IEEE Transactions on Systems,Man,and Cybernetics:Part B Cybernetics,2004,34(4):1907-1916.
[16]Ojala T,Pietikainen N,Harwood D.A comparative study of texturemeasures w ith classification based on featured distributions[J].Pattern Recognition,1996,29(1):51-59.
[17]Dalal N,Triggs B.Histograms of oriented gradients for human detection[C]//Proceedings of the 2005 Conference on Computer Vision and Pattern Recognition,San Diego,USA,Jun 20-26,2005.Piscataway,USA:IEEE,2005,1:886-893.
[18]Wan Yuan,LiHuanhuan,Wu Kefeng,etal.Fusionw ith layered featuresof LBPand HOG for face recognition[J].Journal of Computer-Aided Design&Computer Graphics,2015,27(4):640-650.
附中文参考文献:
[9]丁鑫,陈晓红,陈松灿.核诱导距离度量的鲁棒典型相关分析[J].计算机科学与探索,2012,6(8):708-716.
[18]万源,李欢欢,吴克风,等.LBP和HOG的分层特征融合的人脸识别[J].计算机辅助设计与图形学学报,2015,27(4):640-650.

GU Gaosheng was born in 1992.He is an M.S.candidate at Jiangnan University.His research interests include pattern recognition andmachine learning.
顾高升(1992—),男,江苏兴化人,江南大学硕士研究生,主要研究领域为模式识别,机器学习。

葛洪伟(1967—),男,江苏无锡人,1992年于南京航空航天大学计算机系获得硕士学位,2008年于江南大学信息学院获得博士学位,现为江南大学物联网工程学院教授、博士生导师,主要研究领域为人工智能,模式识别,机器学习,图像处理与分析。在国际权威期刊、会议和国内核心期刊上发表论文70多篇,主持和承担了国家自然科学基金等国家级项目和省部级项目近20项,获省部级科技进步奖多项。

ZHOU Mengxuan was born in 1993.She is an M.S.candidate at Jiangnan University.Her research interests include pattern recognition and image processing.
周梦璇(1993—),女,江苏宝应人,江南大学硕士研究生,主要研究领域为模式识别,图像处理。
Robust CanonicalCorrelation Analysis Based on Generalized M ean*
GUGaosheng1,GEHongwei1,2+,ZHOUMengxuan1
1.Schoolof Internetof Things Engineering,Jiangnan University,Wuxi,Jiangsu 214122,China
2.Key Laboratory of Advanced Process Control for Light Industry(M inistry of Education),Jiangnan University,Wuxi,Jiangsu 214122,China
Canonical correlation analysis(CCA)is amultivariate statisticalanalysismethod which aims atsearching for the linear correlation between two sets of variables of same object.And the criterion function based on L2 norm ofm inimum mean square error used in CCA results in robustness problem.Generalizedmean has been proved to be robust in theory,and has
validation in some applications,such as clustering,object recognition.This paper develops a robust CCA based on generalized mean(GMCCA),which successfully overcomes the drawback that CCA is sensitive to outliers.Themethod notonly inhibits the influence of outliers to achieve robust results,butalso avoids the problem of singular covariancematrix in smallsize of samples.Experimentsonmultiple feature database(MFD),face database(ORL)and objectdatabase(COIL-20)demonstrate theeffectivenessofGMCCA.
generalizedmean;mean squareerror;canonical correlation analysis;robustness;robustcanonicalcorrelation analysis
wasborn in 1967.He received the M.S.degree in computer science from Nanjing University of Aeronautics and Astronautics in 1992,and the Ph.D.degree in control engineering from Jiangnan University in 2008.Now he is a professor and Ph.D.supervisor at School of Internetof Things Engineering,Jiangnan University.His research interests include artificial intelligence,pattern recognition,machine learning,image processing and analysis.
A
:TP391.41
*The Research Innovation Program for College Graduates of Jiangsu Province underGrantNo.KYLX15_1169(江苏省普通高校研究生科研创新计划项目);the Priority Academ ic Program Developmentof Jiangsu Higher Education Institutions(江苏高校优势学科建设工程资助项目).
Received 2016-05,Accepted 2016-07.
CNKI网络优先出版:2016-07-14,http://www.cnki.net/kcms/detail/11.5602.TP.20160714.1616.008.htm l
摘 要:典型相关分析(canonical correlation analysis,CCA)是一种寻求同一对象的两组变量之间最大相关性的多元统计方法,其基于L2范数的最小均方误差(mean square error,MSE)的准则函数对于野值点非鲁棒。广义均值不仅在理论上被证明是鲁棒的,而且在聚类和对象识别等应用中获得了有效性验证。将广义均值应用于CCA,提出了一种基于广义均值的鲁棒CCA(CCA based on generalized mean,GMCCA),成功克服了CCA对野值点敏感的不足。一方面,通过抑制野值点对准则函数的影响,达到鲁棒的效果。另一方面,GMCCA避免了高维小样本导致协方差矩阵奇异的问题。在多特征手写体数据库(multiple feature database MFD)、人脸数据库(ORL)和对象图像数据库(COIL-20)上的实验结果验证了该算法的有效性。

