创设活动情境 体验学习过程

吴祖海

摘 要：《新数学课程标准》指出：学生的数学学习内容应当是现实的、有意义、富有挑战性的，这些内容要有利于学生主动地进行观察、实验、猜测、验证、推理等数学活动。在课堂中，创设活动情境所关心的不是活动的结果，而是活动的过程，有助于学生主体意识的萌发和培养。

关键词：活动情境；实践探索；数形结合；学有所用

创设活动情境，对于扩大学生的视野、拓展知识面、促进思维的发展、培养创新意识和综合素质都起到积极的作用。然而在传统的教学目标、陈旧的教学方法、单调的课堂交流、枯燥的教学训练的数学课堂上，学生用数学的机会很少。本文将在数学课堂中创设活动情境，感悟实践探索、领会数形结合思想和体会学有所用这三个方面展开论述。

一、设置活动情景，感悟实践探索的过程

对实际问题进行观察、思考、探索得出结论，在数学教学中尤为重要。在数学课堂中可安排学生进行探索性的活动，通过一些具体的操作，亲自实践，然后由学生对问题进行思考，得出数学结论，培养学生解决问题的能力和探索问题的精神。可安排的探索性活动有很多，如提供不同长度的小木条搭三角形，有的可搭成，有的则不行，以此探索三角形三边关系。例如，探索正方形的对角线的性质时，由于学生都有折飞机的经验，在上完初二数学的四边形这章后，设计如下活动：

我发给每个学生一张16K的白纸，分四人一小组按下列的步骤进行操作。

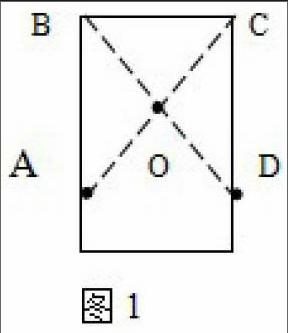
步骤（1）：沿虚线AC边相对折，B、D重合。

步骤（2）：沿虚线OD对折，A、C重合。

步骤（3）：展开后，再折，使A、B重合，C、D重合成图1的形状。

学生通过一起思考，一起试着折叠，一起讨论。在想、做、说的过程中，互相启发、互相融合，结果小组学生完成以下的活动报告单：

最后教师布置作业：你能用图1的纸折出平行四边形、菱形或其他的图形吗？

二、设置活动情景，领会数形结合思想的过程

教学中应当有意识、有计划地设计教学活动，引导学生体会数学之间的联系，感受数学的整体性，不断丰富解决问题的策略，提高解决问题的能力。例如在教学因式分解时，准备多个长方形和正方形卡片（如图）

教师任意写出一个关于a和b的二次三项式，此二次三项式需能分解成两个一次因式的积，且各项系数都是正整数，如a2+2ab+b2，a2+4ab+4b2，2a2+5ab+2b2等；学生根据教师给出的二次式，选取相应种类和数量的卡片，尝试拼成一个矩形；讨论该矩形的代数意义；由学生随意选取适当种类的卡片，拼接成不同尺寸的矩形，回答该矩形表达的代数公式。学生在这一活动中，体会了代数与几何之间的联系，领会数形结合的思想。

三、设置活动情景，体会学有所用的过程

在课堂上创设活动情境，完成了一次对数学知识的探索、发现的过程，使学生真正体验到“学为之用”的道理。例如，在上概率与统计时，模拟了“转盘”小游戏。

活动工具：一块圆形纸板，一根带剑头的竹条，一颗小铁钉。

在圆形纸板上画12个扇形格子，顺次编上号，做成一個圆盘；竹条不带剑头的用小铁钉固定在圆盘中心，做成一个可以转动的指针。学生课前根据教师的提示也作了相应的道具，课堂上学生心存悬念，充满热情。

游戏：假设在圆盘的1号、3号、5号、7号、9号、11号格子里放上价值10元的物品，在2号、4号、6号、8号、10号、12号格子里放上价值5角钱的物品。谁交上1元钱，就可转一下圆盘，等指针停转后，指到哪一格（转到界线上重转），便根据那格的数，从下一格起，按格往下数这个数，数到哪一格，放在格里的物品就归谁。

教师边演示边说明游戏规则，学生热情高涨，跃跃欲试，心想：盘子上，奇数和偶数格子各占一半。数到偶数亏“5角钱”；数到奇数得“10元钱”，可就赚了。“1元钱”不多，可以碰碰运气。全班学生根据规则都在积极的进行游戏，几次尝试后谁都没得到“10元”大奖，都赔了。这时就有同学对这个游戏产生了怀疑，是不是老师在做什么假啊？或者是有什么其他的原因？实际上这个游戏不管做多少次永远也得不到“10元钱”大奖，原因是奇数+奇数=偶数，偶数+偶数=偶数。这就是说，不管指针指在奇数还是偶数格了，最后数到的总是偶数格，赚的可能性是零。通过这次活动，让同学们学到奇偶性原理，同时让他们学了数学，要会用数学才行，否则不就“上当”了吗？

在数学课堂教学中，教师只有转变教育观念，充分尊重学生、信任学生，以学生为主体，以活动为载体，与学生密切合作，才能诱发学生的学习动机，从而充分调动学生学习的积极性、主动性、自觉性和创造性。教师应结合教学内容，设计出利于学生参与的教学环节，运用各种教学手段，创设一个学生可参与的学习情境、学习时间、学习空间、一个良好的氛围等以及指导学生参与的方法，极大地调动学生思维的积极性，发挥其学习的主观能动性，使他们把数学学习成为自觉的学习活动，使学生真正成为课堂教学的主体。

参考文献：

[1]史宁中.数学课程标准教师读本[M].北京师范大学出版社.

[2]伊红，钟旭红，陈士军.初中数学教学案例专题研究[M].浙江大学出版社.