关注过程，提升实效

解祥峰

[摘 要] 随着新课程改革的深化，“过程与方法”作为增补的一个维度的教学目标让我们教师越来越多地意识到“学习过程”的重要性，关注学生的学习过程能够切实提升学生的数学核心素养，关注需要我们教师在问题的设计上更用心，需要我们对学生解题的过程和结果有统计与分析.

[关键词] 高中数学；过程与方法；问题

新课程提出了三维教学目标，“过程与方法”是其中的一个维度，关注学生的学习过程是落实学生是学习的主体这一理念的重要保障，同时也意味着我们教师在教学过程中要改变传统的灌输式的数学教学方法，把引导学生的主动学习和探讨作为教学活动的中心环节，唯有如此才能有效达成过程与方法目标，对于高中数学学科教学而言如何做到关注学生的学习过程呢？笔者认为需要我们教师精心设计问题，需要对学生的问题解决过程有足够的关注，需要有足够的耐心引导学生从思维障碍中走出.

[?] 课前情境的设计，引导学生自主加工和处理信息

对学生学习过程的关注应该从课前的自主预学开始，预学的过程是学生将原有知识和经验作为资源进行信息加工和处理的过程，无论是新授课还是复习课，都应该引导学生高质量地完成这个过程. 对于高中数学这门学科，我们在情境的设计上应该尽可能地做到形象化、直观化，这样有利于信息的调取.

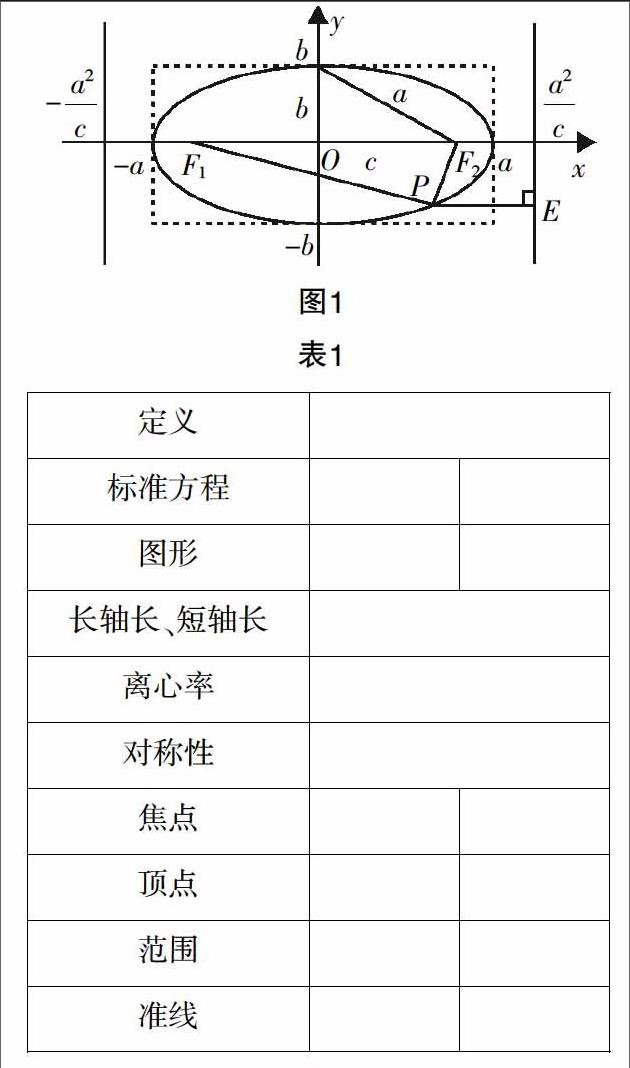
例如，“椭圆的方程复习”笔者设置了如下两个情境，引导学生在课前进行信息加工和处理.

情境1：说说和椭圆相关的知识有哪些？并根据你所了解的知识填写表格.

设计意图：这样的设计有助于“过程与方法”目标的达成，首先借助于图1，学生在图像直观的带领下，思维发散完成形到数的转化，把几何关系转化为代数关系的思维过程，再借助于表格，引导学生对所学知识进行及时的回顾和总结，有利于学生充分掌握知识，厘清关系，为应用知识奠定基础.

[?] 课内设计问题串，帮助体验思维的过程

传统的教学模式下，教学目标是单维度的，就是教给学生知识，考试似乎成为对学生知识面和方法面的考查. 随着课程改革的深化，我们越来越多地认识到学生思维过程的重要性，而思维过程是不可灌输的，我们在平时的课堂教学过程中如何帮助学生体验思维的过程呢？笔者认为可以通过问题串的设置帮助学生体验思维的过程，深化对数学概念的本质的认识.

下面以“函数单调性”重难点的突破为例，笔者设计了如下的问题串，帮助学生深入理解“任意”二字的含义.

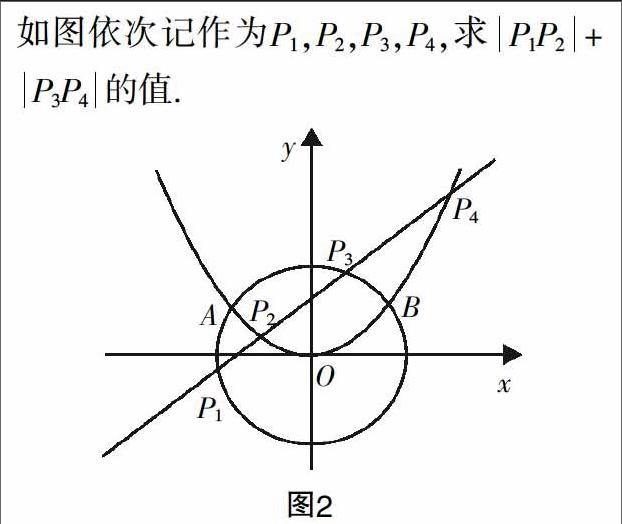
问题1：对于函数f（x）=x2，如果有f（-1）

问题2：对于函数f（x）=x2，如果有f（1）

问题3：x1，x2是区间[0，+∞）上任意的两个数，如果x1

设计意图：“函数单调性”定义的表述中“任意两个”是经常用到的字眼，学生面对这样的表述必然经常是心有疑虑的，因此，教师在教学中要引导学生感知“任意两个”这种数学语言表达的重要性和必要性，激发学生的对比和思考，而且，“如何想到从任意两点的变化方向这个角度来研究该函数属于单调递增函数还是单调递减函数”正是教学的难点，也是“用局部点的性质刻画整体性质”这一数学领域中经常用到的方法. 函数单调性的定义，要求对任意的x1、x2都要成立，即取遍所有的变量x. 学生的思维基础在哪里？如果仅仅是采用反证法，“若命题不成立，则要举反例来说明”，那么，学生的思维是没有得到发展的. 处于这样的思考，笔者在教学中进行了上面问题的设计，通过问题的设置，将“单调性概念”的理解具体化、形式化，这也是学生在分析解决问题的过程中必须解决的一个环节. 为了使学生的理解能力能够突破题意，教师在教学过程中设置了一系列的问题，有针对性地引导启发学生的思考和学习，达到教学的初衷和目的.

当然，对于高一的学生而言，其思维能力和理解能力是有限的，也是参差不齐的，在一节课的教学中，要达成学生对于某一个具体的概念（如上面的函数单调性）有深入理解是不可能的，学生对概念的理解也是有一个过程的. 因此，教师在教学中，要先从直观的表述或者画图开始，使学生先建立对概念表象的初步认知，然后把学生的认知层面逐步提高上升至深度理解的理性层面，把围绕核心问题设置的疑问链精心地思考设计好，并且根据学生各个阶段的学习状况恰如其分地穿插进问题设计的环节，使学生对数学原理理解得更为深刻，在体验思考并解决问题的过程中使学生的思维能够得到有序的发展与提升.

[?] 课外统计与调研学生解决问题的过程，引领学生走出困惑

对学生学习过程的关注不仅仅在课堂内，还应该延伸到课堂之外，尤其是对学生作业完成情况的过程性评价与分析. 很长一段时间，我们对待学生课后作业完成情况都是采用的结果性评价，即统计有多少人做错了，错的人多就上课统一讲评一下正确的做法，如果错的人不多则在作业本上用红笔写上大大的“订正”二字. 这样的处理方式有对学生学情的了解，但是缺乏对学生思维过程的调研，不利于过程与方法教学目标的达成，实践经验表明，教师不能仅仅凭借于学生对于问题解答的最后结果，尤其是关注学生解题过程中出现了怎样的错误，反思学生出现错误的根源在哪里，是知识障碍，还是思维障碍，在讲评的过程中要展示学生的错误，引导学生以学习小组为单位，分析错在哪里，同时有针对性地引导学生自己归纳小结、反思与纠错，使得学生在这个过程中提升自身的认知与探究能力. 下面就以一个具体的作业题进行分析.

作业：如图2所示，点A与点B是圆x2+y2=12和抛物线x2=4y的两个交点，其中，抛物线的焦点记作为F，有一条直线l经过点F且其斜率是1，该直线分别与圆和抛物线相交，且有四个不一样的交点，

学生作业完成过程调研：学生作业完成的过程反映了他对于知识点掌握的情况，以及他在实际解答的过程中思维的方向，笔者可以掌握学生的学情，从学情出发，笔者再和学生一起进行探究、反思和纠错，一般来说，学生作答有以下几种情形.

情形1：对于知识点的掌握无法贯通，以致思维一团混乱，无法解答；

情形2：对于P1，P2，P3，P4的坐标基本能够尝试解出，但是无法进行下一步的作答；

有针对性地组织讲评：对于学生解题大致会出现的情况有了一定的了解后，笔者注意找出学生错误的原因，并且在题目讲评时，在学生错误的关键点上进行引导和点拨，启发学生首先独立思考，反思自己解题中的薄弱点，再一次分析与尝试，试着找准解决问题的方向，提升自己的思维能力和解决问题的能力，当然也有可能再一次尝试后，有部分学生还是找不到正确的解题思路，怎么办？在学生独立思考的基础上，将学生作业暴露出来的错误的情形投影到大屏幕上，以学习小组为单位，大家来找茬，这样的做法不仅仅关注了学生作业完成的过程，还丰富了学生从困惑中走出来的过程，学生对数学概念的印象和理解会更加的深刻.

总之，在教学改革日趋深入的当下，我们教师应该意识到知识的传授只是新课程标准中教学目标的一个方面，对于高中数学来说，“过程与方法”相对其而言是重要的教学目标，关注“过程与方法”目标的达成是培养学生数学能力和素养的重要抓手，也是顺应新的课程理念改变课堂教学模式的必然产物.不仅如此，大量高中数学教学实践的经验表明，“过程与方法”教学目标的达成能够深化学生对知识的理解与掌握，即能够助推知识与技能目标的达成；同时学生经历了过程的体验，对数学学习的兴趣变浓了，解决困难的意志变强了，即能够帮助学生形成正确的情感、态度和价值观.