对三角函数“诱导公式”几种导入方案的对比评说

马娟平

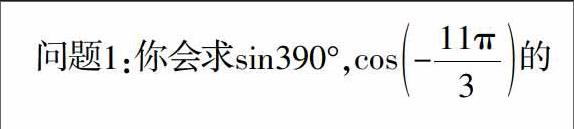
[摘 要] 本文记录在一次区级的评优课中几位参赛选手引入“诱导公式”的不同方案，然后笔者深入分析不同方案的优劣以及适用性，提出针对不同的学生要有不同的“课堂引入”，让“引入”能提高学生的学习兴趣，提高学生对新知识的接受能力和理解能力，最终提高学生对数学的理解.

[关键词] 诱导公式；课堂引入；教学方案；教学方案评说

在一次针对必修4中“1.2.3三角函数诱导公式”（第一课时）数学评优课中，几位选手的设计，在自然、思维及有效性等方面各有千秋. 我们知道，良好的开端是成功的一半，那么如何设计课堂导入更能贴近学生，更能激发学生的兴趣，更趋合理？以下选取几节有代表性的课堂导入，谈谈笔者的一些想法，与同行交流.

[?] 教材简析

三角函数的诱导公式是三角函数的基础，诱导公式的认知基础是终边所对角的三角函数定义、单位圆坐标表示、三角函数线. 教学目标是借助单位圆推导出正弦、余弦的诱导公式，能正确运用诱导公式将任意角的三角函数转化为锐角三角函数，并解决有关三角函数的求值、化简及证明问题.方法是从特殊推广到一般，涉及转化思想、数形结合思想.

[?] 方案呈现

1. 方案1：复习引入

（1）在平面直角坐标系中，任意角α的正弦、余弦、正切是如何定义的？

学生由任意角的三角函数定义得：sinα=_____，cosα=_____，tanα=_____.

（2）为简单起见，取r=1，选取角α的终边与单位圆的交点为P（x，y）.

则sinα=_____，cosα=_____，tanα=_____. 此时P点的坐标可表示为_____.

探究新知：

请在单位圆中作出390°角的终边，交圆周于点P，并根据任意角三角函数的定义求出：

sin390°=______________；

cos390°=______________；

tan390°=______________.

探究一：角的终边与角α的终边相同的三角函数值之间的关系. （略）

2. 方案2：问题串引入

的值吗？

教师（解说）：大家可以看到，这两个角的特征，一个大于360°，一个小于0°，这类角的三角函数值，该如何求？

让学生探索1～2分钟，说说想法.

通过画图，發现390°的终边与30°的终边相同.

教师：终边相同的角的三角函数值有什么关系？

学生：相同.

教师：为什么？

过渡句：公式一可以将任意角的三角函数值，转化为[0，2π]内的角的三角函数值.那么对于[0，2π]内非锐角的三角函数，能否转化成锐角三角函数呢？

3. 方案3：教材引入

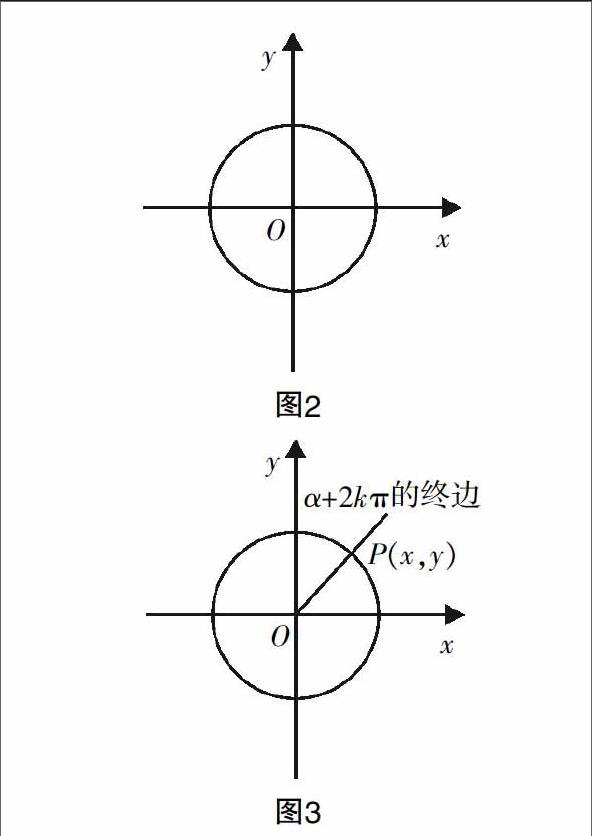
由三角函数的定义可以知道，终边相同的角的同一三角函数值相等，即

sin（α+2kπ）=__________（k∈Ζ）；

cos（α+2kπ）=__________（k∈Ζ）；

tan（α+2kπ）=__________（k∈Ζ）.

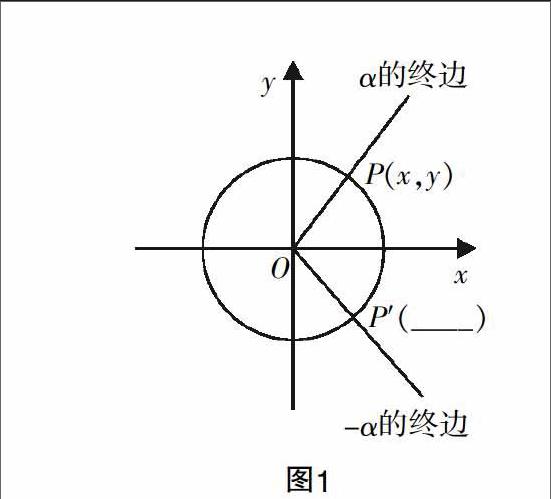
除此之外还有一些角，它们的终边具有某种特殊关系，如关于坐标轴对称、关于原点对称等，那么它们的三角函数值有何关系呢？如果角α的终边与角β的终边关于x轴对称，那么α与β的三角函数值之间有什么关系？

然后，设α与β与单位圆交于点P，P′，则P，P′关于x轴对称，点P的坐标是（cosα，sinα），点P′的坐标是（cosβ，sinβ），则cosβ=cosα，sinβ=-sinα. 得到sin（-α）=-sinα，cos（-α）=cosα，tan（-α）=-tanα.

其他的类似可以求得.

4. 方案4：谈话式导入

教师：前面，我们已经学习了任意角，范围扩大到大于360°或小于0°，学习了三角函数的定义、象限角及同角三角函数的关系式，研究三角函数的一个重要问题就是求值. 对于0～90°的角，借助数表或计算器都能求它们的三角函数值；对于90°～360°的角，大于360°的角，小于0°的角，该如何求它们的三角函数值呢？

我们先研究如何求大于360°的角和小于0°的角的三角函数值.

比如，sin390°=______. 请你尝试解决一下.

学生画出390°，部分学生联想到单位圆，在单位圆上作出390°的角，其终边交圆周于点P.

教师巡视，问：对你画出的角有什么发现？

学生会发现390°的角的终边与30°的角的终边相同，教师要接着问“终边相同的角的三角函数值有什么关系”.

生：根据任意角三角函数的定义，可得sin390°=sin30°.

教师：那么cos390°=_____，tan390°=_____.

学生轻松得出. （略）

教师：这个结论能推广吗？30°改成锐角α可以吗？

学生不难得出：sin（360°+α）=sinα；cos（360°+α）=cosα，tan（360°+α）=tanα.

教师：当α为任意角时，公式还成立吗？

……

[?] 对四种课堂导入方案的对比评说

新课程的基本理念是以学生的发展为本，一个好的教学方案，必须符合教学目标，符合学生的认知特点，因为数学学科的一个重要任务是培养学生的思维能力. 因此，课堂导入是否能产生思维的愤悱状态，是否有利于学生进行思维训练，是非常关键的. 而“强扭的瓜不甜”，学生对不自然的导入不容易接受，因此，要考虑课堂引入的自然性；又“兴趣是最好的老师”，故课堂导入要考虑是否能激发学生的学习兴趣；当然，课堂导入还要有益于学生理解数学，所以还应考虑引入的有效性.由此，对以上四种方案进行简要对比评说.

方案1是先复习旧知，从任意角的三角函数定义到单位圆上点的坐标，然后从单位圆中作出390°角的终边进行探索.这样从已知到未知，并融入数学文化：從布龙克尔（英）名句“圆是第一个最简单、最完美的图形优化设计”，循序渐进，学生循着教师的步伐“走”，很容易走稳，对知识容易理解，但都是教师事先安排好的，适宜于层次较低的学生.不足点：铺垫偏多，留给学生思考的余地不大，长此以往，学生就会产生思维上的惰性，在面临新问题时束手无策，缺乏经验，容易形成畏难心理. 方案1对学生的思维训练显得不足，有教师牵着学生走之嫌.

方案2是基于哈尔摩斯的名言“问题是数学的心脏”进行的问题驱动，先后提出了两个富于挑战性的计算问题. 问题1旨在研究对于大于360°的角或小于0°的角的三角函数求值，从解决问题的需要研究新知；问题2是为了引出需要求解在第四、第二、第三象限的角的三角函数值的问题而设置的，若设角α是第一象限角，则让学生说出-α，π-α，π+α分别是第几象限角. 问题1和问题2的共同点都是为了解决学习这五组诱导公式的必要性问题. 弄清了为什么要学习新知，明确了方向，就会产生自觉的行动. 问题3是诱导公式的基础，也是学生理解的难点，即（cosα，sinα）. 若问题3解决了，则三个角-α，π-α，π+α的终边都可以用三角函数值表示. 这三个问题解决好了，这五组诱导公式的意义建构就完成了. 这种方案是从解决问题的角度出发的，促使学生产生愤悱的状态，产生解决问题的愿望，凸显其必要性. 这种方案有益于培养学生的思维能力，这种方案适宜于层次中等或中等以上的学生.

方案3是通过两个角α，β特殊的对称关系，求出单位圆上对应的坐标关系，得出诱导公式. 提出的问题很自然，叙述简约、清楚，也有利于学生理解数学，适宜层次中等及中等以下的学生.其不足点是没有问题驱动来得强烈，不利于学生求知欲的激发.

方案4是对教材方法的一种改造，通过与学生的对话引入. 其一，从已知逐渐过渡到未知，顺应学生的认知基础，符合学生的认知规律，与学生做朋友，容易激发学生的兴趣，形成了和谐的课堂氛围；其二，引入、过渡很自然，亦步亦趋，易于学生操作，有益于教学生学会学习，今后遇到类似问题，学生也会类似地解决；其三，注重知识的前后联系，其后教师的提问“当α为任意角时，公式还成立吗？”为诱导公式的理解、记忆做好了铺垫.

我们知道，铺垫有益于学生的理解，但不利于培养学生的思维；跳跃思维不利于学生的理解，但能促使学生思考，培养他们的思维. 限时的课堂教学实践表明：教学需要一定的铺垫.因此，要求教师基于学情，把握好铺垫的度，而这个铺垫（即导入）是教师谱写优美教学乐章的前奏，是师生情感共鸣的第一个音符，也是课堂教学艺术的重要组成部分. 著名特级教师于漪曾说过：“课的第一锤要敲在学生的心灵上激发他们思维的火花，就像磁石一样把学生牢牢吸住.” 由此可见，导入对于一堂课的成功与否非常重要，所以我们要重视课堂的导入.