基于RomaxCLOUD的高速内圆磨削主轴轴承优化设计

高泉流，刘译励，周海波，张进华

(1.西安交通大学 机械制造系统工程国家重点实验室，西安 710049；2.洛阳轴承研究所有限公司，河南 洛阳 471039)

随着加工向高速、高精度方向发展，为了有效提高内圆磨削主轴的临界转速和轴端刚度，要求配套轴承具备高刚度、高精度、低温升以及长寿命等性能。文献[1]对原有批量生产的内圆磨床电主轴的轴承结构进行改进，达到了加宽刚度调整范围，提高轴承寿命的效果；文献[2]通过确定支承轴承配对形式对高速内圆磨削主轴临界转速和轴端刚度的影响关系，给出了在电主轴实际应用中支承轴承配对形式的选择原则；文献[3]基于传递矩阵法和有限元法分别对内圆磨削电主轴的临界转速和刚度进行计算，得出2种方法的差异；文献[4]通过波纹的频率分析和激振试验中的机械系统的固有模态分析对比，得到深孔内圆磨削震颤的主要因素是主轴刚度不足，进而提出改进方案；文献[5]通过对万能外圆磨床主轴上采用的“三块瓦”式滑动轴承进行改进，采用动静压轴承，使得外圆磨床精度、效率及主轴寿命都大大提高。

轴承结构参数对轴承性能有至关重要的影响，但上述关于内圆磨削主轴轴承优化的研究并未涉及到轴承参数，且优化方法较为复杂，计算量大。鉴于此，基于RomaxCLOUD轴承设计与仿真系统，以轴承刚度、最小油膜厚度、疲劳寿命和轴承沟道接触应力为优化目标，对高速内圆磨削主轴常用配套角接触球轴承的内圈沟曲率半径系数、外圈沟曲率半径系数、球数、球组节圆直径及球径等参数进行优化设计。

1 RomaxCLOUD系统简介

RomaxCLOUD 轴承设计与仿真分析系统是洛阳轴研科技股份有限公司与英国 Romax 科技有限公司共同研发并且拥有完全自主知识产权的高级轴承设计仿真分析云服务协同创新平台[2]。其内置了圆锥滚子轴承、深沟球轴承、角接触球轴承、圆柱滚子轴承、滚针轴承5种轴承数据库以及轴承的尺寸公差、形位公差标准数据库，可实现标准和非标轴承的参数化设计。RomaxCLOUD 是专业的轴承性能仿真工具，以RomaxDesigner为仿真内核，基于经典的轴承分析理论和国际标准，考虑系统对轴承的影响，仿真计算更加精确,可对轴承的刚度、寿命、载荷分布、位移、接触应力、润滑油膜分布等进行分析计算。

2 优化设计方法

2.1 模型求解思想

求解变量为内圈沟曲率半径系数fi、外圈沟曲率半径系数fe、球数Z、球组节圆直径Dpw、球径Dw，Z取值为满足一定约束条件的整数值，Dw取值为满足条件的一系列国际规定的离散值，Dpw，fi，fe为满足条件的连续值。若采用一般的优化方法，优化结果需人为调整为标准值，故采用穷举法。穷举法是在满足约束条件的范围内列出所有设计方案，进行寻优，从而得到最佳设计。若要在RomaxCLOUD中实现这一目标，需将Dpw，fi，fe离散化。设计变量较多时，需列出全部设计方案，计算量大，故采用正交试验优化设计方法[7]。

2.2 多目标函数优化法

在实际问题中，对于大量的工程设计方案要评价其综合性，往往要考虑多个目标，例如，在轴承设计中，通常会考虑高转速、高刚度、高承载、长寿命等。但一些指标是互相矛盾、对立的，需要进行协调，以便取得对各分目标函数值来说都比较好的方案。功效系数法是根据多目标规划原理，对每项评价指标确定一个满意值和不允许值，以满意值为上限，以不允许值为下限，计算各指标实现满意值的程度，并以此确定各指标的分数，再经过加权平均综合，从而评价被研究对象的综合状况。

2.3 目标函数加权系数确定

根据工程实际情况和生产经验确定目标函数的权重，相对重要的函数权重取大一点，不重要的取小一点。对于用于磨削加工的角接触球轴承，首先关注的是轴承疲劳寿命，其次是影响精度的最小油膜厚度和轴承刚度，最后是最大接触应力。因此，取疲劳寿命L10权重系数为w1=0.3，轴承刚度J的权重系数w2=0.25，最小油膜厚度λ的权重系数w3=0.25，最大接触应力σ的权重系数w4=0.2，建立多目标函数的统一目标函数为

W=w1f(L10)+w2f(J)+w3f(λ)+w4f(σ),

(1)

W值越大,说明方案越优。

3 实例分析

3.1 变量参数

以高速内圆磨削主轴配套角接触球轴承7014C为例，轴承参数为：D=110 mm，d=70 mm，B=20 mm，α=15°。根据设计经验fi取0.505，0.510，0.515，0.520;fe取0.515，0.520，0.525，0.530。根据RomaxCLOUD轴承设计与仿真系统里内嵌的约束条件，球数Z取16，17，18，19；球组节圆直径Dpw取90，90.5，91，91.5 mm；球径Dw取12，12.303，12.5，12.7 mm。

3.2 主轴实际工况假设

高速内圆磨削主轴实际工况：n=12 000 r/min，轴向载荷Fa=300 N，径向载荷Fr=2 000 N，建立的轴系模型如图1和图2所示。

图1 轴系模型示意图

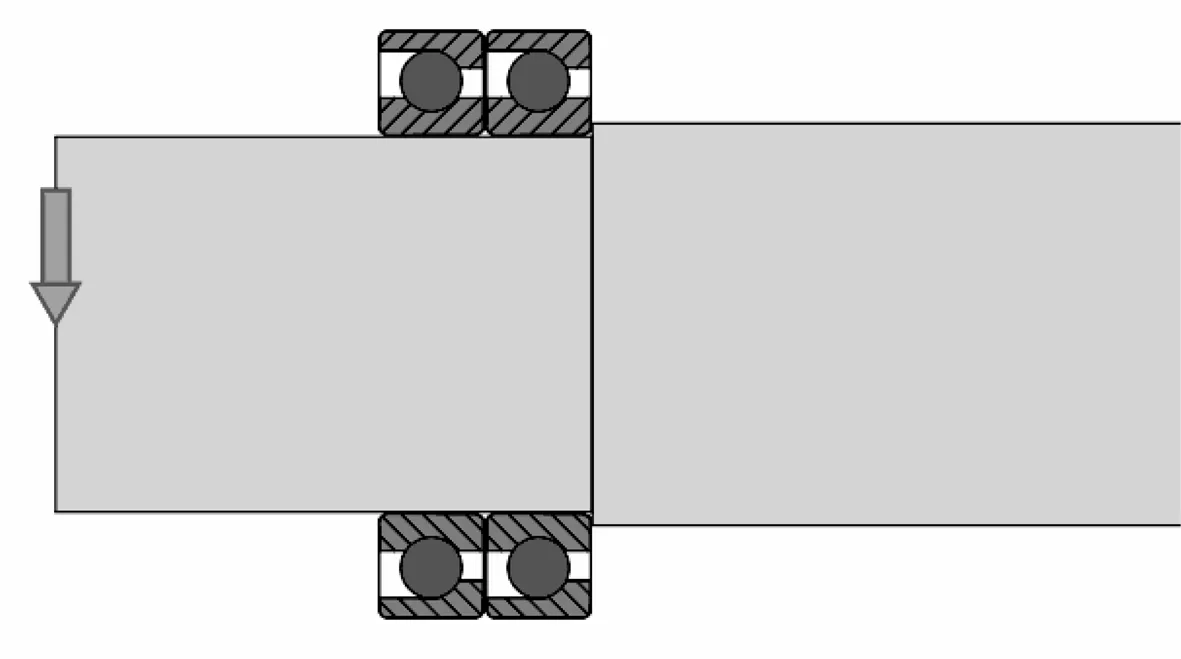
图2 轴系模型局部放大图

3.3 正交试验及其计算结果

根据设计经验以及RomaxCLOUD轴承设计与仿真分析系统里内嵌的球径约束条件、球组节圆直径约束条件、球数约束条件选定正交试验的因素及水平见表1。

若按全面试验要求，需进行1 024种组合试验，尚未考虑每个组合的重复数，故采用L16(45)正交表安排试验，只需进行16次,仿真计算轴承主参数及正交试验结果见表2，极差分析见表3。由表3可知，各个参数对目标函数的影响从大到小依次为：A>E>B>C>D,可得到最优组合为fi=0.505，fe=0.515，Z=19，Dpw=90 mm，Dw=12.7 mm。由于上述的最优水平组合未出现在正交试验中，故通过RomaxCLOUD系统对试验结果进行验证。由表4可以看出，通过RomaxCLOUD轴承设计与仿真系统优化设计可大大提高轴承的性能。

表1 正交试验优化设计因素及水平

表2 仿真计算轴承主参数及正交试验结果

表3 试验结果的极差分析

表4 最优水平组合试验结果

4 性能分析

极差分析表明，内、外圈沟曲率半径系数对主轴性能的影响较大，基于RomaxCLOUD轴承设计与仿真系统分析内、外圈沟曲率半径系数对轴承最大接触应力、轴承刚度和寿命等性能的影响。

4.1 最大接触应力

当Z=19，Dpw=90 mm，Dw=12.7 mm时，最大接触应力随内、外圈沟曲率半径系数的变化如图4所示。内、外圈沟曲率半径系数增大，沟道最大接触应力增大，且最大接触应力随内圈沟曲率半径系数变化的增幅大于外圈沟曲率半径系数。

图4 最大接触应力随沟曲率半径系数的变化

4.2 刚度

当Z=19，Dpw=90 mm，Dw=12.7 mm时，轴承刚度随内、外圈沟曲率半径系数的变化如图5所示。内、外圈沟曲率半径系数增大，轴承刚度减小，轴承刚度随内圈沟曲率半径系数变化的降幅大于外圈沟曲率半径系数。

图5 轴承刚度随沟曲率半径系数的变化

4.3 寿命

当Z=19，Dpw=90 mm，Dw=12.7 mm时，轴承寿命随内、外圈沟曲率半径系数的变化如图6所示。轴承寿命随内圈沟曲率半径系数的增大而增大，随外圈沟曲率半径系数的增大而减小。

图6 轴承寿命随沟曲率半径系数的变化

5 结论

1)基于RomaxCLOUD轴承设计与仿真系统综合使用多目标函数优化方法以及正交试验对高速内圆磨削主轴配套轴承进行优化设计，最终得到最优结构参数。

2)基于RomaxCLOUD轴承设计与仿真系统分析内、外圈沟曲率半径系数的变化对轴承最大接触应力、轴承刚度和寿命等性能的影响情况。在一定条件下，增大内、外圈沟曲率半径系数，沟道最大接触应力增大，轴承刚度降低。增大内圈沟曲率半径系数会使轴承寿命增大，增大外圈沟曲率半径系数则会使轴承寿命减小。