突破三棱锥外接球半径的六种策略*

甘肃临泽一中(734200) 魏正清

突破三棱锥外接球半径的六种策略*

甘肃临泽一中(734200) 魏正清

三棱锥的外接球问题中,如何以三棱锥为载体求解外接球半径,解法灵活多变,对空间能力想象的要求非常高.若能利用长方体、三棱锥的性质、三棱锥底面外心或侧面外心、过三棱锥的底面上一边作对棱的截面,则可极大的简化运算,巧妙探索外接球球心或半径.

三棱锥,外接球,半径,策略

三棱锥的外接球问题,可较好的考查学生的空间想象能力,逻辑推理能力和运算求解能力,它既是教学的难点,也是高考经久不衰的热点.如何巧妙的寻找球心、探索球半径,突破这一解题瓶颈,是解决此类问题的关键.本文给出六种策略,旨在抛砖引玉.

1.利用长方体的面对角线探索外接球半径

例1三棱锥中则三棱锥的外接球的表面积为___.

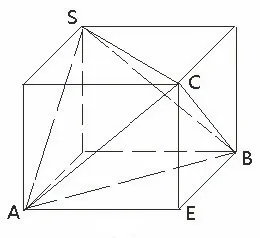
图1

分析如图(1),在长方体中,设AE=a,BE=b,CE=c.则S C=AB=从而a2+b2+c2=14=(2R)2,可得S=4πR2=14π.故所求三棱锥的外接球的表面积为14π.

评注三棱锥的相对棱相等,探寻球心无从着手,注意到长方体的相对面的面对角线相等,可在长方体中构造三棱锥,从而巧妙探索外接球半径.

2.利用长方体的体对角线探索外接球半径

例2在正三棱锥S−ABC中,点M是SC的中点,且 AM⊥SB,AB=则正三棱锥的外接球的表面积为( ).

A.6π B.12π

C.32π D.36π

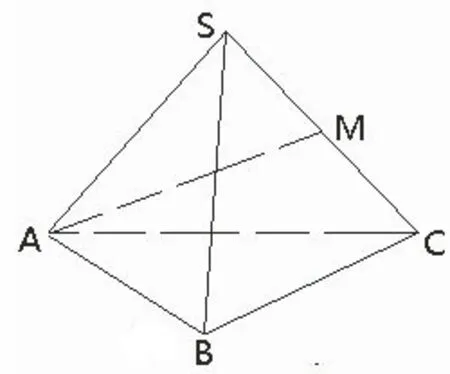
图2

分析如图(2),因三棱锥S−ABC是正三棱锥,知SB⊥AC.又AM⊥SB,知SB⊥平面SAC,从而SB⊥SA,SB⊥SC.同理SA⊥SC,知SA,SB,SC为某长方体的长、宽、高且SA=SB=SC=2.于是(2R)2=3×22=12,可得S=4πR2=12π.故所求三棱锥的外接球的表面积为12π.

评注利用正三棱锥中相对棱互相垂直这一性质,可巧妙的探索侧面三角形的顶角特征,进而构造长方体,利用长方体的面对角线,化繁为简,探索外接球半径.

3.利用底面三角形的外心构三角形探索外接球半径

图3

分析如图(3),依题意AC=CB=R,设点O1为△ABC的外心,则OO1⊥底面ABC.依

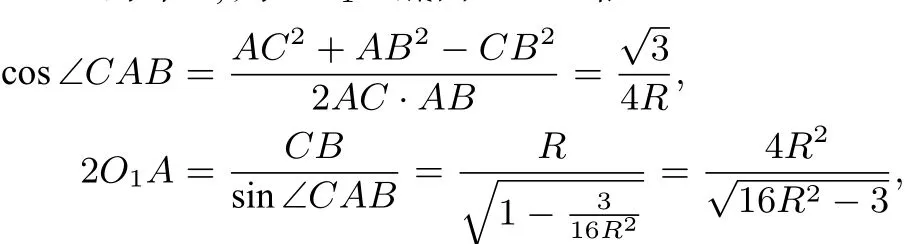
则

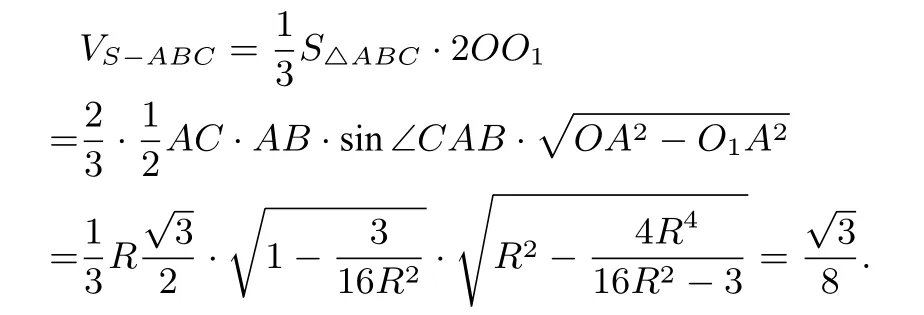
可得球半径R=1.

评注 利用球心与三棱锥底面三角形外心连线垂直于底面这一性质,可构造直角三角形,有的放矢,巧求外接球半径.

4.利用底面三角形与侧面三角形的外心探索球心

例4√平面四边形ABCD中,AB=AD=CD=1,BD=2,BD⊥C 其沿对角线BD折成四面体A′BCD,使平面 A′B 平面 BCD. 若四面体 A′BCD的顶点在同√一个球面上,则该球的体积√为( ).

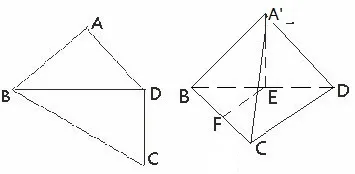
图4

分析 如图(4),设BD,BC的中点分别为E,F.因点F为底面直角△BCD的外心,知三棱锥A′−BCD的外接球球心必在过点F且与平面BCD垂直的直线l1上.又点E为底面直角△A′BD的外心,知外接球球心必在过点E且与平面A′BD垂直的直线l2上.因而球心为l1与l2的交点.又FE//CD,CD⊥BD知FE⊥平面A′BD.从而可知球心为点F.又A′B=A′D=1,CD=1知 BD=,球半径

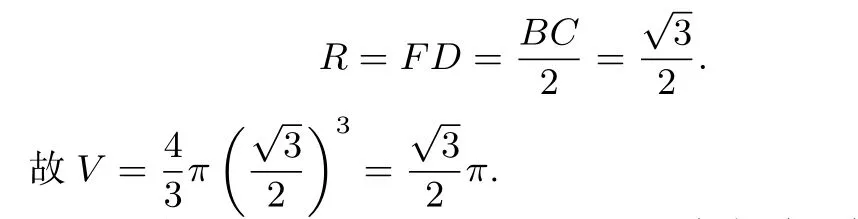
评注 三棱锥侧面与底面垂直时,可紧扣球心与底面三角形外心连线垂直于底面这一性质,利用底面与侧面的外心,巧探外接球球心,妙求半径.

5.利用三棱锥过对棱中点的截面探索球心

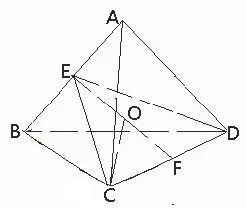
图5

评注紧扣三棱锥相对棱相等这一特征,构建过对棱中点的截面,可巧妙探索球心,出奇制胜,迅捷解题.

6.利用与三棱锥对棱垂直的截面探索外接球半径

例6已知三棱锥S−ABC的所有顶点都在球的表面上,△ABC是边长为l的正三角形,SC为球的直径,且三棱锥S−ABC的体积为,则三棱锥S−ABC外接球的体积为___.

分析如图(6),因SC为球的直径,AC=BC=1知△SAB△SBC. 过点 A作 AD⊥SC 于 D,则BD⊥SC,故 SC⊥ 平面 ADB.取AB中点E,则从而可得R=1,从而外接球的体积

图6

评注以球的直径为斜边的两个三角形全等时,可做与球的直径垂直的截面,构三棱锥,巧妙探索外接球半径.

*甘肃省十二五规划课题“新课程背景下数学课堂教学情景中师生关系重建研究”(课题批准号GS[2015]GHB1415)成果.