例谈解析几何问题的平面几何解法

广州大学数学与信息科学学院(510006) 钟木超

例谈解析几何问题的平面几何解法

广州大学数学与信息科学学院(510006) 钟木超

法国著名数学家笛卡尔17世纪创立解析几何以来,有一类几何问题可以代数化,运用代数的方法研究其几何性质,从而得到解决这类问题的通法,极大地促进了代数与几何的发展.其中获益最大的无疑是圆锥曲线问题.这类问题的解法几乎都是通过将几何条件代数化来完成的,从而成为了解析几何的重要内容.但是解析几何问题本质是几何问题,它们本身就包含一些很重要的几何性质.如果我们可以充分利用这些几何性质,它们其实就是纯几何问题,完全可以借助平面几何的知识加以解决.这样不但能避开繁琐的代数运算,使解决问题的过程得到简化,而且更好地揭示这些问题的几何本质.例如三类圆锥曲线的定义及其光学性质本身就是极其重要的几何性质.下面笔者通过一些例子展示如何运用平面几何解法解决解析几何问题,希望可以达到抛砖引玉的效果.

一、圆锥曲线的光学性质

定理1从椭圆的一个焦点处发出的光线照射到椭圆上,经椭圆反射后,反射光线通过另一个焦点,且经过反射点的镜面所在的直线为椭圆的切线.

定理2从双曲线的一个焦点处发出的光线照射到双曲线上,经过双曲线反射后,反射光线的反向延长线通过另一个焦点,且经过反射点的镜面所在的直线为双曲线的切线.

定理3从抛物线的焦点处发出的光线照射到抛物线上,经过抛物线反射后,反射光线平行于抛物线的轴,且经过反射点的镜面所在的直线为抛物线的切线.

注 这三个定理分别描述了椭圆、双曲线、抛物线的光学性质.其证明读者可参阅文[1].

二、用平面几何方法解解析几何问题的例子

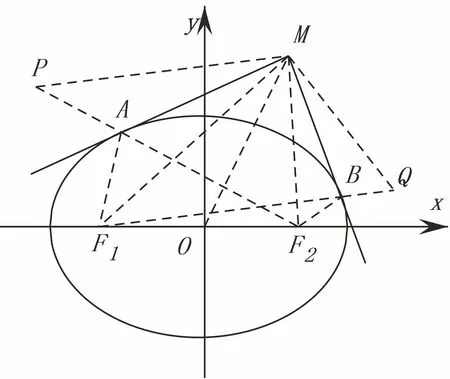
图1

证 如图1,设F1,F2分别是椭圆的左右两个焦点,分别作F1,F2关于切线MA,MB的对称点P,Q,连结MP,MQ,PA,QB,AF1,AF2,

注 此例是2014年广东数学高考圆锥曲线压轴题(第20题文理共用)的推广,原题如下:已知椭圆=1的一个焦点为

(I)求椭圆方程;

(II)若动点P(x0,y0)为椭圆外一点,且点P到椭圆的两条切线相互垂直,求点P的轨迹方程.

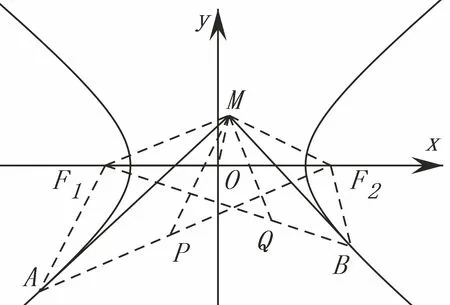
图2

证 如图2,设F1,F2分别是双曲线的左右两个焦点,分别作F1,F2关于切线MA,MB的对称点P,Q,连结MP,MQ,PA,QB,AF1,PF2,QF1,BF2,MF1,MF2,OM.由定理2易得A,P,F2;B,Q,F1分别三点共线,所以PF2=AF2−AP=AF2−AF1=2a,同理QF1=2a=PF2,又因为MF2=MQ,MP=MF1,所以

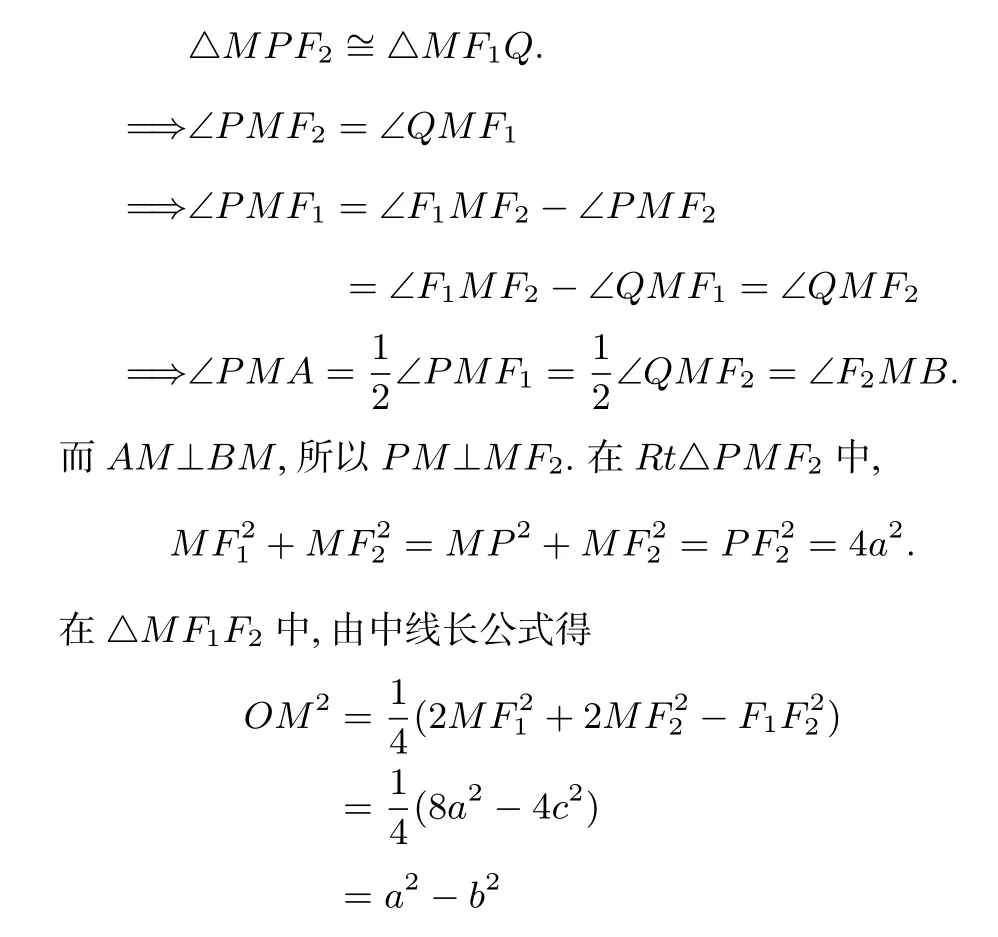
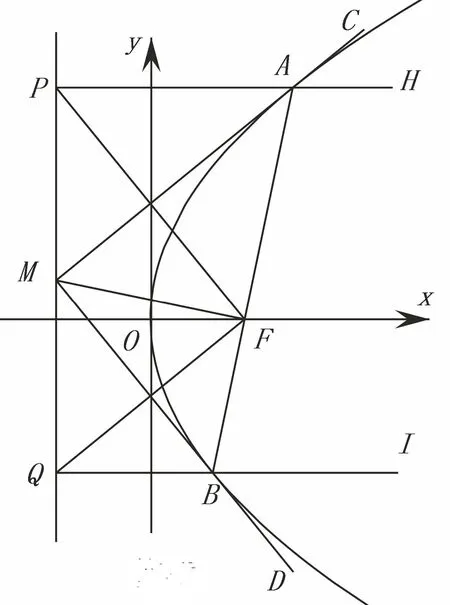
图3

即M的轨迹方程为x2+y2=a2−b2.

例3 M是抛物线C:y2=2px(p>0)的准线l上的一点,过点M 的直线与抛物线相切于A,B,分别过A,B作l的垂线,垂足分别为P,Q,设抛物线的焦点为F,连结PF,QF,MF,AF,BF,求证:(1)MF⊥AB;(2)PF⊥QF;(3)AM⊥BM;(4)A,F,B三点共线.

证 如图3,作射线PA,QB,由定理3易得∠CAH=∠MAF=⇒ ∠MAF= ∠CAH= ∠MAP. 又因为AP=AF,AM=AM,所以 △AMP ∼= △AMF=⇒∠AFM= ∠APM=90◦,MF=MP,∠PMA= ∠FMA.同理 ∠BFM= ∠BQM=90◦,MF=MQ,∠QMB=∠FMB.所以 MF⊥AB,MF=MP=MQ,∠AMB=∠AMF+ ∠BMF=∠QMF=90◦=⇒AM⊥BM,F在以 PQ为直径的圆上,即 PF⊥QF.由AP=AF,PM=FM 得 ∠AFP= ∠APF,∠MPF=∠MFP.同理 ∠BFQ= ∠BQF,∠MQF= ∠MFQ.所以∠AFP+∠MFP+∠MFQ+∠BFQ=∠APF+∠MPF+∠MQF+∠MFQ=180◦,即A,F,B三点共线.

例4 证明:椭圆的焦点在椭圆切线上的射影的轨迹是以椭圆的中心为圆心,且过长轴顶点的圆.

证 先证左焦点的情形.如图

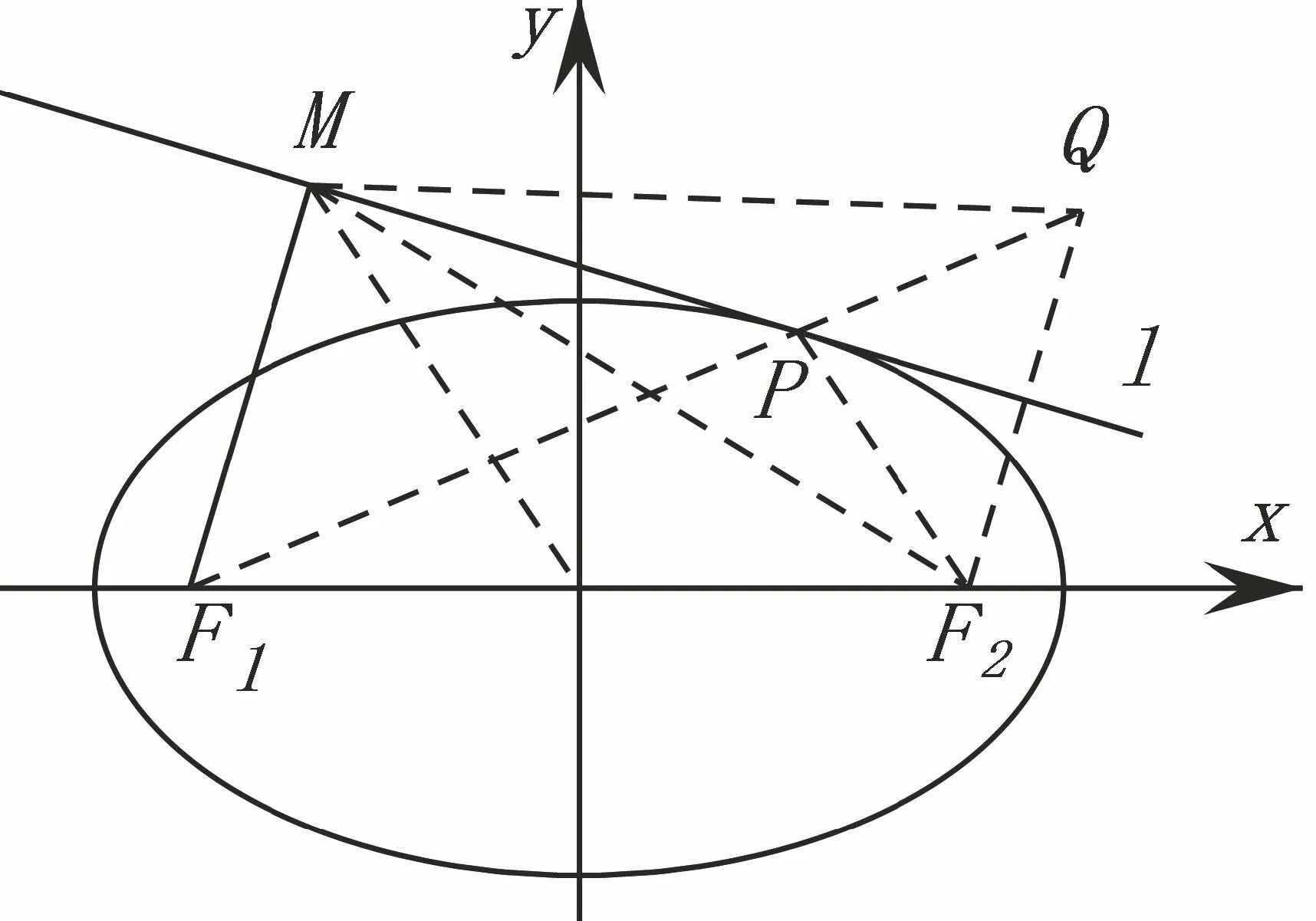
图4

在△MF1F2中,由余弦定理得2MF1·MF2·cos∠F1MF2①+②并整理得在△MF1F2中,由中线长公式得

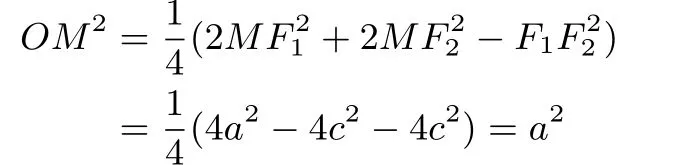
故M的轨迹为以O为圆心,a为半径的圆.

对于右焦点的情形,同理可证,不再赘述.

注 此例是《数学通报》2012年第11期刊登的第2087号问题.供题人用解析法证明了该问题.

类似的性质对于双曲线和抛物线也成立,从而得到下面的定理5和定理6,因为其证明根据前四例的方法容易给出,有兴趣的读者可以尝试自己给出证明,这里就不再赘述.

定理5双曲线的焦点在双曲线切线上的射影的轨迹是以双曲线的中心为圆心,且过实轴顶点的圆.

定理6 抛物线的焦点在抛物线切线上的射影的轨迹是经过抛物线的顶点且垂直于其对称轴的一条直线.

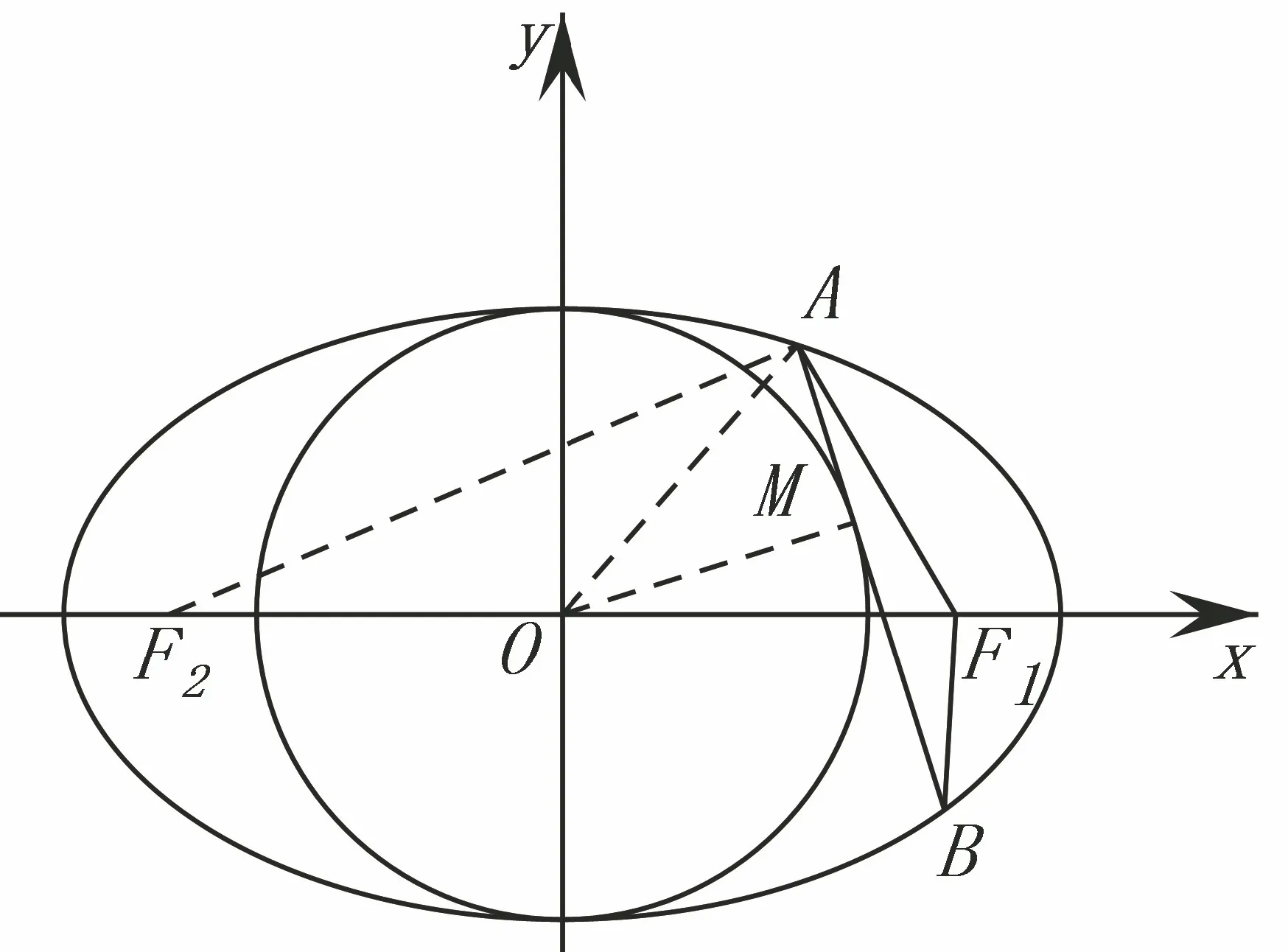
图5

解 如图5,连结AF2,OA,OM,设AF1=x,则AF2=2a−x.在Rt△OAM 中,由中线长定理可得,

即AM=a−x.所以AF1+AM=a.同理BF1+BM=a.从而△ABF1的周长为2a.

三、总结反思

上面五个例子可以看出,利用平面几何知识解决解析几何问题,不但可以避开繁琐的代数运算,简化解题过程,而且解法简洁优美,更好地体现了圆锥曲线的几何性质.因此对于解析几何问题,不应一味地运用解析法,而应该将解析法和平面几何方法相结合,从而得到解决问题的最优解法,同时可以更好地提高解题能力.

[1]郇维中.同一法证明圆锥曲线光学性质及应用举例[J].数学通报,2011,6;46 53.