基于小波框架的非局部曲面去噪

李晓慧，王 聪

（河海大学 理学院，江苏 南京 211100）

基于小波框架的非局部曲面去噪

李晓慧，王 聪

（河海大学 理学院，江苏 南京 211100）

提出了一种基于小波框架的非局部曲面去噪方法。该方法首先平滑了曲面法线方向上的平均曲率，然后根据基于小波紧框架的变分模型校正了含噪声曲面。变分模型由正则项和保真项构成。其中，正则项为包含小波框架的L1范数项，保真项为离散曲面的平均曲率和点坐标的最小二乘项之和。最后，进行了数值实验验证了所提出模型和算法的有效性和实用性。

小波框架；非局部曲面去噪；平均曲率；Laplace-Beltrami

现实生活中，使用三维扫描仪获得曲面的同时往往夹杂着许多噪声，例如：高斯白噪声，脉冲噪声等。从一个非光滑的曲面上去除噪声并且保持其原有特征，即为曲面去噪。近些年来，曲面去噪越来越受到各国学者的关注，尤其是三角网格曲面去噪。

变分曲面去噪模型和基于PDE的曲面去噪模型[1-5]，在过去十多年已取得了很大成功。Deschaud[6]提出了一种基于曲面离散点集的非局部去噪方法，即用设计好的距离方程描述局部曲面，近而根据变分模型去噪。Yoshizawa[7]也提出了类似地非局部去噪方法，不同的是用局部径向基函数替代了原先的最小二乘函数。Gilboa[8]提出一个非局部扩散过程是由一个加权差分的非局部二次方程的快速下降得到的，近而也得到了相应的快速去噪方法。最近，Dong[9]引进了一个非局部的热方程用来曲面去噪，即用设计好的距离函数定义相似权重，且在一个隐式曲面上，用一个水平集公式解决了PDE演变。

文中一种基于小波框架的非局部曲面去噪方法，不但实现了非局部曲面扩散流在网格曲面上表示，而且实现了小波框架在三家网格曲面的应用。第一步，通过多次迭代过程，光滑了一个三角网格曲面法线上的平均曲率；第二步，操作含噪声的曲面去适应这个处理过的光滑的法向量曲率场，即建立了曲面去噪的变分模型，并且在变分模型中引入了小波框架。实验证明，该方法可以有效地去除曲面噪声且保持曲面细节。

1 理论基础

1.1 符号定义

一般地，含噪声的曲面模型S軌可表示为

其中，ε为噪声扰动，Nor∈Rn3为曲面离散点的法线，S为原始曲面。令三角形网格M表示一个光滑曲面M的一个分段线性近似。M的图表集用（Ω，S）表示，Ω奂R2是一个开的参考域，S是相一致的坐标映射。三角网格曲面M由三角形Ti（i=1，…，Ni）的集合T（覆盖M）和定点Si（i=1，…，Nv）的集合S来定义，这里Si表示第i个顶点。

在变分去噪公式中，本文引入一个关键算子，即Laplace-Beltrami算子。在M上的Laplace-Beltrami算子是作用于一个光滑函数η上的局部算子，记作ΔM。在三角网格曲面M上Laplace-Beltrami算子ΔM是的离散化，记为L，且其在顶点Si的值由下式给出：

离散的小波紧框架已经得到了广泛应用[11-13]。在离散的情况下，一个图像是一个二维的数组，这个数组可被理解为处于离散网格下的一个向量。离散的小波紧框架的分解可被表示为一个矩阵乘法w，相应地，通过酉扩展原理[14]，可以得到重构算子 wT，并且wTw=I。在实现的过程中，两个矩阵乘法通过用快速的张量积来实现紧小波框架的分解和重构，实质上就是通过一系列的滤波器做图像的卷积。

但是，由于曲面和图像之间的拓扑结构的不同，因此不能直接应用小波框架来进行曲面去噪。最近，Fan[15]通过在Hilbert空间里进行双重Gramian分解，构造了非张量积紧小波框架，Dong[11，16]引入了一个曲面的多尺度的表示，构造了一个数据矩阵和相一致的小波框架矩阵。三角形网格M=（S，T），顶点集S：= {S（k），k=1，2，…，n}，顶点 S（k）的（x，y，z）坐标表示为S（k）=（S1（k），S2（k），S3（k））T。对于每个k=1，2，…，n，如果顶点S（k）的度为6，就可找到S（k）的6个相邻点，且定义为{P（k，1），P（k，2），…，P（k，6）}。 对于每个i=1，2，3，数据矩阵Fi由邻近点的函数值的集合和在顶点的函数值的集合组成，Fi是R7×n中的一个矩阵，定义如下

这里，（P1（k，j），P2（k，j），P3（k，j））T，j=1，2，…，6是P（k，j）的（x，y，z）坐标。定义F={F1，F2，F3}。最后，如果一些顶点的度d小于6，用这d个邻近点值的平均值来产生剩余的个邻近点值；如果d大于6，将选取其中6个值来生成。

接下来，Dong[11]定义了一个面具矩阵U∈R7×7，即

其中，U的第1行是一个低通滤波器，U的第2-7行是高通滤波器。

在U中，每个滤波器的系数与顶点的邻域是协调的。下面定义曲面上的1层小波分解算子为：

这里α：={α1，α2，α3}， 矩阵αi=UFi。 重构算子 wT可定义为

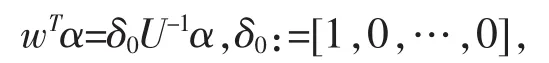
行向量u：=[1，1，1，1，0，0，0]是U-1的第一行，且uU=δ0=[1，0，……，0]。因此，定义wT为wT（α）=u（α）= {u（α1），u（α2），u（α3）}，显然，wTwS=S。

1.2 非局部变分光滑

在定义域Ω上，考虑下面函数的极小化

其中，λ>0是正则化参数，W是一个带权重的梯度算子。相一致的Euler-Lagrange扩散流可表示为：

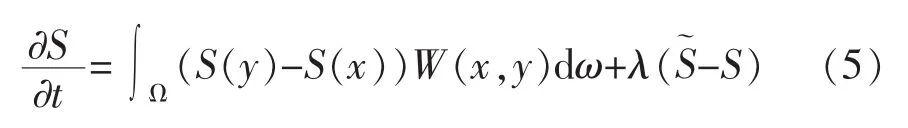
其中，x，y∈Ω，W（x，y）是权重函数。这里W（x，y）满足W（x，y）≥0且是对称的，即W（x，y）=W（y，x）。

在三角网格曲面M上，式（5）的离散化形式为

这里Si表示S在第i个顶点的值（i=1，…，Nv），N（i）是与第i个顶点相连的点的集合。

对于xyz坐标下的Sk（k=1，2，3），式（6）的规范化形式变为

若使Wij=ωij且ωij由式（3）定义，则式（7）可用平均曲率流在M上的空间离散化来表示，即

其中，S0是初始曲面，从左边起，式（8）的第一项是正则项，第二项是保真项。

由于对于曲面方程来讲，平均曲率是一个梯度流，因此，平均曲率流有着很强的正则化作用。在离散背景下，平均曲率流用一定的速度在法线方向上移动每个顶点，等于平均曲率在顶点的离散近似。

根据式（2），本文提出了下面的非局部算子，即M上的带权的Laplace-Beltrami算子

其中，ωij如（2）定义，而Wij取决于第i个顶点和第j个顶点之间的相似性度量。

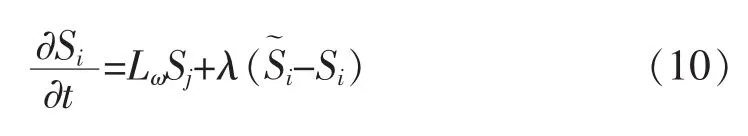
2 基于小波紧框架的曲面去噪

设H是三角网格曲面M上的平均曲率，它由曲面的两个主曲率累加得到，即H（S）=k1+k2。是法线的平均曲率向量场。

对于三角网格曲面，式（9）中权重的选择方式，应该描绘两个局部曲面块间的相似性，本文采用平均曲率值来刻画。因此，定义下面的权重

其中，参数σ控制两个区域块的相似性大小。

文中提出一种基于小波紧框架的非局部曲面去噪方法。这个曲面去噪方法这个非局部方法由下面的算法描述，在第一步通过一系列线性形式解决式（11），接着在第二步最小二乘问题中，插入光滑的法线平均曲率向量场，通过LSQR迭代方法来解决问题。这里由式（2）定义，Lω由式（9）定义。

算法1

初始化：给定含噪声曲面S軌步骤1：求解H：

3 数值实验

在本节中，选取了3个最常用的三角网格曲面模型‘bunny’、‘elephant’和‘fandisk’进行验证算法效果。在数值实验模拟中，本文在原始模型的法线上加入了均值为0，方差为0.2的高斯白噪声。算法的去噪效果如图1所示。

图1 自上而下：bunny、elephant、fandisk；自左而右：原始曲面、含噪声曲面、去噪后曲面

图2 自上而下：bunny、elephant、fandisk；自左而右：含噪声曲面、Zhang[17]、Ours

从图1可以清晰地看出，本文提出的曲面去噪算法的去噪效果极好，有效地保持住了曲面的棱角细节，例如：bunny模型的耳朵轮廓，elephant模型的眼睛等。

紧接着，文中又将产生的数值实验结果与Zhang[17]中的算法结果进行了对比。对比结果见图2。

由图2可以看出，本文提出的去噪算法的去噪效果普遍优于Zhang[17]中的结果。尤其是对于bunny和elephant两个曲面模型的处理，本文提出的算法更能有效地保持特征细节。

为了进一步说明本文所提出算法的优越性，我们又计算了SNR值。见表1。SNR的表达形式定义如下：

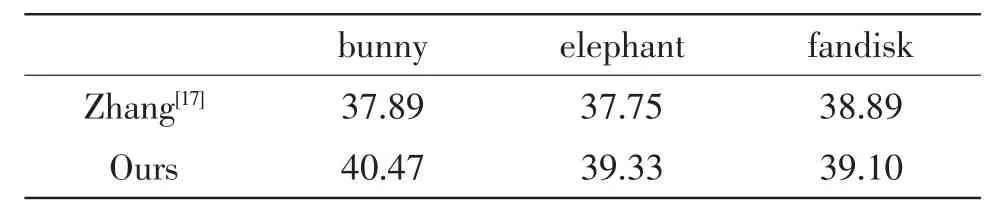
表1 SNR值的比较

由表1不难看出，本文得到的去噪结果的SNR全部高于Zhang[17]，这说明了本文所提出的去噪算法不仅视觉上优越于Zhang[17]，而且数值上也优越于Zhang[17]。因此，该算法具有一定的推广价值。

4 结 论

文中提出了一个基于小波框架的非局部曲面去噪的变分方法。该方法首先平滑曲面法线方向上的平均曲率，然后根据含小波紧框架的最小二乘模型校正了曲面。实验证明该方法能有效地去除曲面上的噪声，同时保持住有效地曲面细节特征。因此，在工程应用中，具有一定的推广意义。

[1]Clarenz U，Diewald U，Dziuk G，et al.A finite element method for surface restoration with smooth boundary conditions[J].Computer Aided Geometric Design，2004，21（5）:427-445.

[2]Xu G， Pan Q， Bajaj C L.Discrete surface modelling using partial differential equations[J]. Computer Aided Geometric Design，2006，23（2）: 125-145.

[3]Tasdizen T，Whitaker R，Burchard P，et al. Geometric surface processing via normal maps[J]. ACM Transactionson Graphics，2003，22（4）: 1012-1033.

[4]Ohtake Y，Belyaev A，Bogaevski I.Mesh regularization and adaptive smoothing[J].Computer-Aided Design，2001，33（11）:789-800.

[5]Morigi S.Geometric surface evolution with tangential contribution[J].Journal of Computational and Applied Mathematics，2010，233（5）:1277-1287.

[6]Deschaud J E，Goulette F.Point cloud non local denoising using local surface descriptor similarity [J].laprs，2010，9（1-3）:109-114.

[7]Yoshizawa S，Belyaev A，Seidel H P.Smoothing by example:mesh denoising by averaging with similarity-based weights[C]//IEEE International Conference on Shape Modeling and Applications. 2006:9-9.

[8]Gilboa G，Osher S.Nonlocal linear image regularization and supervised segmentation [J]. Multiscale Modeling and Simulation，2007，6（2）: 595-630.

[9]Dong B，Ye J，Osher S，et al.Level set based nonlocal surface restoration[J].Multiscale Modeling and Simulation，2008，7（2）:589-598.

[10]Meyer M，Desbrun M，Schroder P，et al.Discrete Differential-geometry operators for triangulated 2-manifolds [J].Mathematicsand Visualization，2014，6（8-9）:35-57.

[11]Dong B，Jiang Q T，Liu C Q，et al.Multiscale representation of surfaces by tight wavelet frames with applications to denoising[J].Applied and Computational Harmonic Analysis，2016，41（2）: 561-589.

[12]Dong B，Shen Z.MRA-based wavelet frames and applications:image segmentation and surface reconstruction[C]//Spie Defense，Security，and Sensing.2012，8401（7）:3837-3849.

[13]Mallat S.A wavelet tour of signal processing:the sparse way[M].Academic press，2008.

[14]Ron A，Shen Z.Affine systems in.The analysis of the analysis operator[J].Journal Function Analysis，1997，148（2）:408-447.

[15]Fan Z T，Ji H，Shen Z.Dual Graminan analysis: duality and unitary extension principle[J].Math. Comp.，2015，85:239-270

[16]Dong B， Jiang Q， Liu C， et al.Multiscale representation of surfaces by tight wavelet frames with applications to denoising [J].Applied and Computational Harmonic Analysis，2016，41（2）: 561-589.

[17]Zhang H，Wu C，Zhang J，et al.Variational mesh denoising using totalvariation and piecewise constant function space[J].IEEE Transactions on Visualization and Computer Graphics，2015，21（7）:873-886.

Wavelet frame based nonlocal surface fairing

LI Xiao-hui，WANG Cong
（College of Science，Hohai University，Nanjing 211100，China）

This paper proposes a wavelet frame based variational model for surface fairing.We extend nonlocal smoothing techniques for image regularization to surface smoothing or fairing，with surfaces represented by triangular meshes.Our method is able to smooth the surfaces and preserve features due to geometric similarities using a mean curvature based local geometric descriptor.We present an efficient two step approach that first smoothes the mean curvature normal map，and then corrects the surface to fit the smoothed normal field.This leads to a fast implementation of a feature preserving fourth order geometric flow.We demonstrate the efficacy of the model with several surface fairing examples.

wavelet frame；nonlocal surface fairing；mean curvature；Laplace-Beltrami

TN919.8

A

1674－6236（2017）10-0178-04

2016-09-22稿件编号：201609203

国家自然科学基金项目（11101120）；中央高校基本科研业务费专项基金项目（2015B38014）

李晓慧（1992—），女，山东聊城人，硕士研究生。研究方向：小波分析及其应用。