轴向载荷下圆柱滚子轴承滚子端面与挡边接触位置的多目标模糊优化设计

张亚军，张雨奇

（1.杭州轴承试验研究中心有限公司，杭州 310022；2.贡比涅技术大学，法国 贡比涅 60200）

在大多数应用中，向心滚子轴承不仅要承受径向载荷，还要承受轴向载荷，带挡边的圆柱滚子轴承是其中之一。文献［1］有关于向心滚子轴承轴向承载能力的介绍。轴向承载能力与材料的疲劳强度无关，而与滚子端面和引导挡边的接触和润滑条件有关。在没有流体润滑时，轴向载荷会使滚子端面和挡边之间产生摩擦，如果载荷条件恶劣，则会迅速发生破坏。而球端面滚子与挡边间易形成油膜，会降低摩擦因数与接触温度。球端面滚子与平端面相比，在较高的轴向载荷下不发生咬合现象。球端面与挡边的接触对于接触应力、接触变形、油膜厚度、摩擦因数、摩擦力矩等均有影响。若想得到最大的油膜厚度、最小接触应力及摩擦因数等，需找到最佳接触位置。

文献［2］介绍了接触位置寻优的一种试验方法，该方法与图解法相同，求解不准确，且计算程序仅考虑了载荷与变形，油膜厚度、摩擦因数等都是把位置确定后再进行核算，其成本较高。鉴于此，通过对接触位置受力及流体润滑分析，建立以接触应力、接触变形、油膜厚度为多目标的模糊优化模型，用模糊优化法求解。并求解最佳模糊水平截集，确定最佳接触位置。引入模糊数学的基本思想，不仅解决了多目标优化问题，同时也兼顾了一些难以用模型来表达的主观和客观因素，得到在不同最优水平值下的优化方案，以供用户选择。

1 模型的建立

1.1 目标函数

滚子端面和挡边接触如图1所示，A为接触点，θ为挡边角度，S为滚子球端面半径，R为滚子半径，h为挡边高度，t为挡边倒角，r为滚道油沟半径，Fr为径向载荷，Fa为轴向载荷。以θ，S为设计变量，假设滚子端面和挡边的接触为球与平面的点接触。

图1 滚子端面和挡边接触Fig.1 Contact between roller end face and rib

1）目标函数1：最小油膜厚度

滚子与挡边接触状态如图2所示，量纲一的最小油膜厚度为［3-4］

图2 滚子与挡边接触示意图Fig.2 Contact diagram between roller end face and rib

式中：U为速度参数；G为材料参数；W′为载荷参数；Q为接触载荷；E0为当量弹性模量；α1为黏度压力系数；n0为黏度；u为平均速度；Rx为曲率半径。

（1）式可化简为

滚子与挡边受力示意图如图3所示，假设滚子球端面与挡边的接触为点接触。

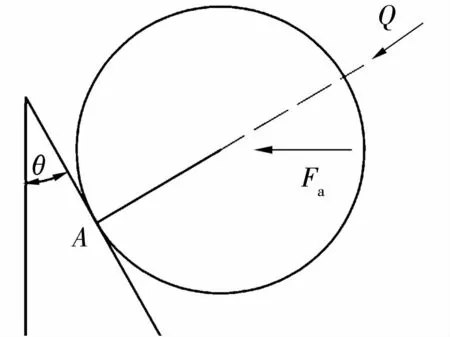
图3 受力示意图Fig.3 Diagram of force

1.2 约束函数

由几何关系可知，滚子与挡边间接触位于挡边倒角与滚道之间，即

1.3 优化模型

以θ，S为设计变量，令 θ＝X（1），S＝X（2），设计变量 X＝［X（1），X（2）］T，最小目标函数

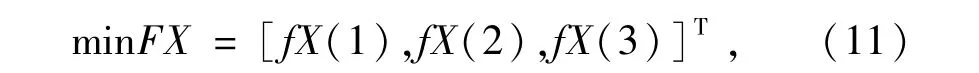
其中：fX（1），fX（2），fX（3）分别为以油膜厚度、接触应力、变形量为目标函数。

约束条件为

2 优化过程及方法

2.1 目标函数的单目标优化

在满足（12）式约束条件的情况下，求 X＝［X（1），X（2）］T。

2.2 多目标优化的设计模型

以fX（1）为目标函数，以 fX（2），fX（3）为约束条件。

2.3 多目标模糊优化设计模型［5-7］

（16）式由于对 fX（2），fX（3）约束太严格，使fX（1）得益较少，其结果偏重 fX（2），fX（3），而且也可能不收敛，可在fX（2）和 fX（3）的约束中加上允许放宽值，约束条件变为

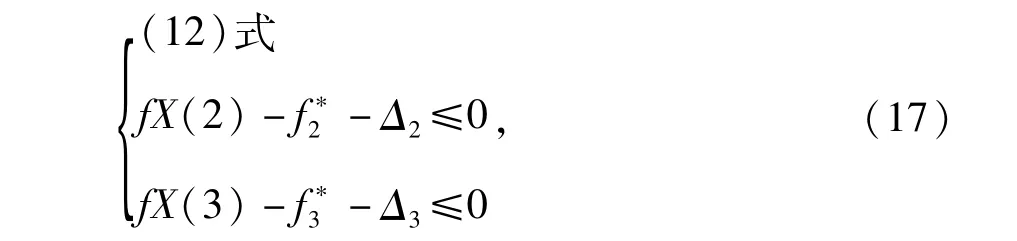
式中：Δ2，Δ3分别为允许放宽值，可引入模糊优化设计确定其值。

模糊优化数学模型与普通优化数学模型类似，只是其中包含有模糊因素（即水平截集）。建立模糊优化模型，需确定隶属函数。所谓隶属函数就是在容许到不容许界限之间的过渡区容许度（隶属度）的变化，变化复杂，但一般取最简单的直线变化（图4中的AC段）。图4中，μ为隶属度；λ为水平截集；P0为模糊函数在过渡区的变化；PT，Pλ分别为其在允许区和不允许区的临界值（B点和C点）。

图4 隶属函数关系图Fig.4 Graph of membership function relation diagram

水平截集为λ，令P＝σ，则应力与隶属度的关系为

2.4 模糊优化模型的求解

模糊优化模型的求解方法有基本解法、最优水平截集法、近似模糊集合法，实际中均很少应用。文献［4］中提出了综合评判求解最优水平截集后，使水平截集法得到广泛应用，下文介绍用综合评判法求解最优水平截集λ*。

设主观不确定因素为：S1为设计力量，S2为加工技术，S3为成本，S4为材料性能，S5为管理水平，则因素集 U＝［S1，S2，S3，S4，S5］，设决断集为α＝［0，0.1，0.2，…，0.8，0.9，1］。

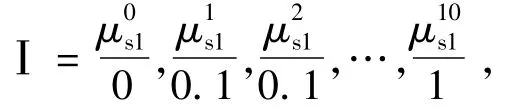
3 优化结果和分析

对滚子球端面和挡边进行多目标优化设计，以NF209轴承为例，其结构参数为：d＝45 mm，D＝85 mm，B＝19 mm，R＝5 mm，h＝2 mm，t＝0.3 mm，r＝0.8。Fr＝10 kN，Fa＝5 kN。

3.1 单目标优化设计

分别对（17）～（19）式求单目标优化并分别计算每种优化状态下另2种情况的结果，见表1。

表1 单目标优化Tab.1 Single objective optimization

3.2 多目标模糊优化设计

设主观因素集 U＝［S1，S2，S3，S4，S5］＝［0.4，0.2，0.2，0.1，0.1］，代入（24）式得最优水平截集，由（21）式得多目标优化设计计算结果：水平截集为0.83，X（1）＝0.03，X（2）＝90.02。

4 结论

1）选取3个目标函数进行优化求解可以平衡轴承的整体性能，结果更接近实际工况，但会损失某单一目标值。综合评判法求解为最优方案。

2）模糊优化设计不仅解决了多目标函数的问题，同时也兼顾一些难以用模型来表达的主观因素和客观因素，使优化方案更接近实际工况。通过模糊化可得到不同的最优方案，以供用户选择。

3）分析结果可指导试验分析，因素集的选取要根据具体制造工艺及经验进行调整。