要答案自己做

文︳陈万龙

要答案自己做

文︳陈万龙

课堂不仅是时时发生错误或出现意想不到的事情的地方，更是师生互相学习、共同发展的天地。意外情况的发生，为师生展示自我提供了契机。然而，部分教师由于备课时过分依赖参考资料，造成了教学上的偏颇或失误，导致教学专业水平下降。其实，数学教师也要“下水作文”：解答问题、探索问题，做到“拳不离手、曲不离口”，才能保持进取精神。教师做题即研究，只有先做题，才可以避免习题的机械重复，使练习做到少而精。教师通过做题，发现题目本身及其答案的疏漏，并促进学生更加深刻地理解知识、掌握技能，领悟数学思想方法。要答案，自己认真做——这是特级教师沈唯刚老师30多年教书生涯的经验总结。对此笔者深有体会，并与大家分享亲身经历的几个小插曲。

一、“老师，这样的做法有问题”

案例1过x轴上一点P向圆C：x2+（y-2）2=1作两切线，切点分别为A，B，则△ABC面积的最小值是（）。

这是高三复习课上的一道题。当时有一位学生给出了与参考答案几乎一样的解答过程。

设AB与PC的交点为E，则S△PAB=B·PE=又因为点P在x轴上，所以PC取最小值时，就是C点到x轴距离的最小值，即PC=CO＝2时，△PAB的面积最小，最小值为。

学生大都认为解答过程没有问题。正当我为此同学的解答感到高兴时，一位同学站起来说道：“老师，这样的做法有问题。”我心里一惊：“有问题！”好在自己还算有点经验：“请把你的想法跟大家说一说。”这位同学不慌不忙地说：“只有当AE= PE时，面积才能取到最小值。但在这里AE=PE是不可能的，并且这样也只能是求出最大值，而事实上，当PC=CO时只能求得最小值。因此，可以肯定这样的做法是有问题的。”真是一语点醒梦中人：“既然取不到，那么怎样求解此题呢？同学们可互相交流、探讨。”几分钟后，有同学上台展示了。随后，我和学生对上述成果进行了认真的分析和细致的研究，一致认为是正确无误的：均是通过设角变量，化为此角变量的函数关系求解，这是处理这类问题的一般方法。

教学反思：教师只有事先认真做题了，才知道已有答案解法的错误。若不是把“球”抛给学生，这个问题的处理必定会失败，甚至有可能使课堂出现冷场局面。教师只有通过事先做题，才能避免这类事情的发生，使自己在课堂上处变不惊。即使是学生在课堂上的展示非常正确，教师也可以有意示错，激起学生探究的热情，更好地促进学生认知的发展。

二、“老师，这道题本身就有问题”

案例2已知椭圆M的两个焦点分别为F（1-1，0），F（21，0），P是椭圆上的一点，|PF1·||PF2|=，且满足∠F1PF2=，则椭圆M的方程是_______。

一位同学上台展示了他的解法：设|PF1|=m，|PF2|= n。由已知得mn=，又由∠F1PF2=，得m2+n2-2mncos=4。从而有（m+n）2=m2+n2+2mn=20，即（2a）2=20，得a2=5。所以b2=a2-c2=4，故椭圆M的方程为=1。

当大部分学生认为此种解法干净利落时，一位数学成绩中等的学生怯生生地说：“老师，这道题本身就有问题。”教室里顿时雅雀无声。该生上台展示了他的解题过程：

设点P（x，y），则有：

我和同学们仔细检查了这两种解法，可以肯定两种解法的思路都正确，解题的恒等变形与推理过程完全正确。这是为什么？我坚信这是编题者忽视了一个重要性质，所能取得的最大值问题。于是我改变教学计划，让学生充分讨论、交流，最后达成共识，得到结论：若椭圆=1（a＞b＞0）上的点P对椭圆两焦点F1，F2的张角θ（0＜θ＜π)余弦值的最小值为-1。此时角θ取得最大值。

教学反思：两位同学的解法跟我的预设没有差别，竟然得出了相互矛盾的结论，这是我始料未及的。我趁机将问题的研究权交给了学生。学生通过充分思考，挖掘思维潜力，有效地促进思维的深度参与。这样看来，教师只有通过先做题，才能了解问题的难易程度，然后抓住错题，变废为宝，让解题指导更具针对性。

三、“老师，我的解法比你的更简单”

这是一次月考中的一道题。从考试的结果看，几乎所有的学生都是按通性、通法求解的，但不是因计算复杂出错，就是因运算量大半途而废，无功而返。为了鼓励学生的信心，我和学生一道进行了详细的解答。

解：由题意知A（-2，0），直线l：y=k（x+2）。

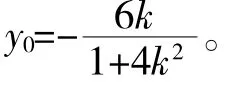
运算确实极其复杂，我要求学生对此解答认真反思，看看有没有值得借鉴的。此时，一位同学说：“老师，我的解法比你的简单多了。”我非常高兴，让他将自己的解法和其余同学一起分享。

解：设B（2x0，2y0），则=1，且线段AB的中点N（x0-1，y0）。

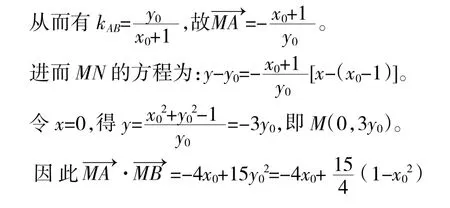
故当x0=-时，取得最大值，为。

学生们对此解法感到非常惊讶也很佩服，我的心情也久久不能平静。此同学利用线段AB的中点坐标将斜率表示出来，而这恰恰抓住了此题的本质特征，真是思之越深，解之越简。

教学反思：学生对本题的简明解法，确实让人赏心悦目，拍案叫绝。学生学习数学的发散思维，在这里也得到了难能可贵的展示。反复回味上述简单解法，他那快捷明朗、机智灵活的思维，恐怕是我们教师都难以做到的。这无疑告诉我们，教师要放下架子，真正做到教学上以学生为主体，以教师为主导，让学生在自主探索、交流合作的过程中获得对数学较为全面的体验，体验做数学的乐趣。教师送给学生一个信任，学生会还你一个奇迹。

四、“老师，此题就只有这样一种解法？”

案例4求函数y=sinx+cosx+sinx·cosx的最大值。

在高三的一次复习课上，我再次选用了这样一个问题。其实，在学习必修课本时就出现过类似的问题，不过，还是有同学不知怎样处理。我给出了如下的解法：

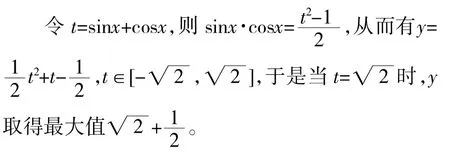
当很多同学都为自己想不到问题的解答而显得有点沮丧时，一个同学站起来说：“老师，此题就只有这样一种解法吗？但这与您平时常说应将此类问题转化为只含有一个角的某个三角函数的关系式不相符。”这位同学提出了一个很值得思考的问题。“不瞒大家说，我确实没有这样想过。今天就借此机会，我们一起来研究研究。”经老师这样一说，同学们热情高涨，跃跃欲试。不一会，同学A进行了如下解答：y=sin（x+）+sin2x，当x=时，sin（x+）与sin2x均能取得最大值1，故有y的最大值为

这样解答真是令人眼前一亮，解答过程不仅简洁、新颖，还突破了惯用的换元法。“本题真的就不能转化为一个角的某个三角函数。”这时同学B上台板演了他的解答：

很明显，这也是一个非常不错的解答。同学A的解法虽然简单，但若求其最小值就无能为力了。而同学B的解法很好地解决了这一问题，可以说同学B的解法更具一般性。

教学反思：在教师都没有想到的情况下，学生通过自身的努力得到了本题的不同解法，可谓是层层递进，突破难点，课堂达到高潮。教学中对问题的解答，教师必须让学生真正参与，及时根据学生的信息反馈对解题过程作出调控。特别是当学生的思路与教师的设想有差距，但对深入地理解问题又具有一定价值时，教师要因势利导，教会学生寻求思路的方法，引导学生分析方法的优劣。只有这样，才能使不同层次学生的解题能力得以提高。

结束语：我们知道教师做题并不比学生高明，有时学生能发现你还未发现的错误与疏漏，学生的解答可能比你的更简洁。教师认真地做题是讲题的必要条件。只有认真研究问题，研究解法、变式，研究学生解决问题时可能出现的难点或疑点，才能在课堂上很好地开发利用动态生成资源，才能在讲解时充分暴露你解题的思维过程，从而使学生在潜移默化中学会分析问题、解决问题的思维方法，真正做到从学会到会学，从会学到会创。

（作者单位：华容县第二中学）