用统一的代换证明两个著名的几何不等式

浙江省开化县第二中学 (邮编：324300)

初数研究

用统一的代换证明两个著名的几何不等式

浙江省开化县第二中学曹嘉兴(邮编：324300)

a2-(b-c)2=(a+b-c)(a-b+c)=(2p-2c)(2p-2b)=4(p-b)(p-c)=4y，

同理可得

b2-(c-a)2=4(p-c)(p-a)=4z，

c2-(a-b)2=4(p-a)(p-b)=4x.

由海伦公式可得

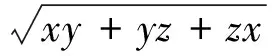
下面就用统一的代换(p-a)(p-b)=x，(p-b)(p-c)=y，(p-c)(p-a)=z，给出两个著名的几何不等式的新证法.

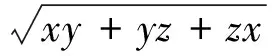
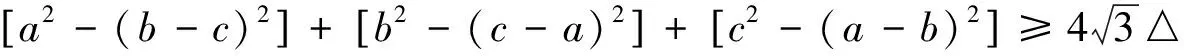
⟺(x+y+z)2≥3(xy+yz+zx)

⟺x2+y2+z2≥xy+yz+zx

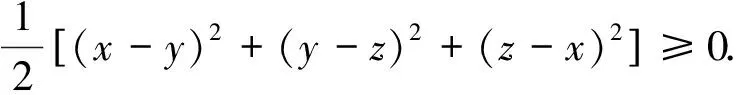
故原不等式成立.

由最后的不等式不难看出当且仅当x=y=z，也就是p-a=p-b=p-c,即a=b=c时，等号成立，故当且仅当△ABC为正三角形时等号成立.

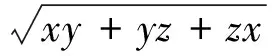
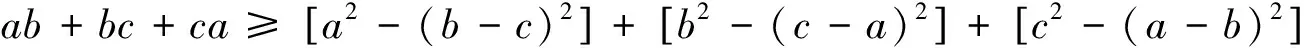
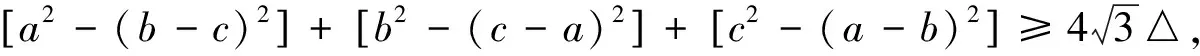
⟺(x+y+z)2≥3(xy+yz+zx)

⟺x2+y2+z2≥xy+yz+zx

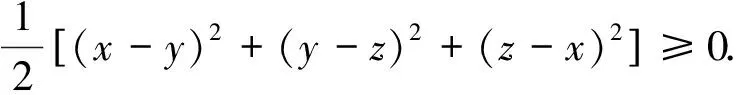
故原不等式成立.

由最后的不等式不难看出当且仅当x=y=z，也就是p-a=p-b=p-c,即a=b=c时，等号成立，故当且仅当△ABC为正三角形时等号成立.

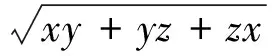
2017-03-19)