基于一种新型趋近律的分数阶Duffling不确定系统的自适应滑模同步
毛北行
(郑州航空工业管理学院理学院,河南 郑州 450015)
基于一种新型趋近律的分数阶Duffling不确定系统的自适应滑模同步
毛北行
(郑州航空工业管理学院理学院,河南 郑州 450015)
基于一种新型趋近律研究了分数阶不确定Duffling系统的自适应滑模同步控制问题,利用自适应滑模方法设计了滑模函数和控制器,得到了主从系统取得自适应滑模混沌同步的充分条件。结果表明:选取适当的控制器以及滑模函数下,主从系统取得滑模混沌同步,给出了严格的推理过程和数学证明,最后仿真算例表明该方法有效。
分数阶Duffling系统; 自适应滑模;混沌同步
Mandelbrot曾指出在自然界中存在着大量的分数维[1-2],采用分数阶对系统进行建模能更好的揭示对象的行为和本质。1995年,Oustaloup并设计了第一代分数阶控制器,研究和对比分析表明分数阶控制器有更好的鲁棒性等优点。分数阶滑模结合了分数阶微积分和滑模控制的双重优点,成为非线性控制的重要方法,并在各个领域也得到了广泛应用[3-9]。文献[10]设计了一类分数阶不确定动力系统的终端滑模控制问题,文献[11]研究了一类不确定系统的自适应滑模终端混沌同步控制问题。本文基于一种新型趋近律研究了分数阶不确定Duffling系统的自适应滑模同步控制问题, 得到了主从系统取得自适应滑模混沌同步的充分条件。结果表明:选取适当的控制器以及滑模函数下,主从系同能取得滑模混沌同步。仿真算例表明该方法有效。
1 滑模趋近律的设计
利用新型幂次函数fal(x,β,δ)[12]设计趋近律,函数定义如下:
(1)
其中β>0,表示幂次函数的指数,0<δ<1,δ为fal(x,β,δ)在原点附近正负对称线段的区间长度,由定义1可知,当x的绝对值小于设定的δ时,x的增益δβ-1较大,反之,增益较小。本文设计如下新型滑模趋近律:
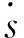
(2)
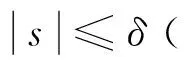
2 系统描述与预备知识
定义1Caputo分数阶导数定义为[13]
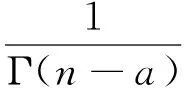
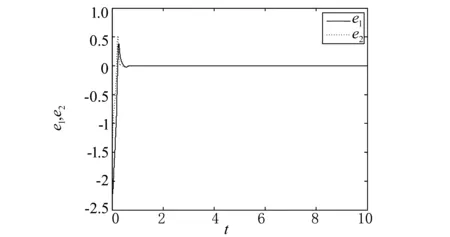
n-1<α 考虑分数阶Duffling混沌系统: (3) 式中,a,b,c均为系统参数,ω表示余弦函数的频率幅值。当a=-1,b=0.25,c=0.5,α=0.873时出现混沌吸引子。以上述系统作为主系统,设计从系统为如下系统: (4) (5) 假设 为正常数。 说明 双曲正弦函数的反函数为 引理1 对任意的x均有,函数 以下分情况讨论:x≥0时,h(x)≥0显然成立。 当x<0时, h′(x)<0 由函数的单调性不难得到在(-∞,0]上h(x)递减,从而 h(x)>h(0)=0 定理1 在假设1下,设计控制器 由于 从而根据分数阶微积分理论,不难得到 Δf(y)+d(t)+u(t)]+ -εs·fal(s,β,δ)-ks·arsh(s)+g(t)s≤ 因ε>0,k>0,s≠0时,由函数fal(s,β,δ)和引理1不难得到,εsfal(s,β,δ)>0,并且ksarsh(s)>0,函数fal(s,β,δ)对自变量s有显著放大作用, 作为分数阶Duffling系统的特例,以下考虑整数阶Duffling混沌系统: (6) 以上述系统作为主系统,设计从系统为如下系统: (7) (8) 因此不难将定理1在特殊情形下的结论平推,得到如下推论: 推论1 在假设1下,设计控制器 上式求导得到: Δf(y) +d(t) +u(t)] + -εs·fal(s,β,δ)-ks·arsh(s)+g(t)s≤ 以下证明部分同定理1,略。 利用龙格库塔法进行数值仿真,系统参数 a=-1,b=0.25,c=0.5,ω=1,α=0.873 定理1中选取 Δf=-0.05siny1,d(t)=0.2cost, β=0.5,δ=0.02,γ=15,ε=15 系统初始值设置为: (x1(0),x2(0))=(0.1,0.2), (y1(0),y2(0))=(0.5,-0.6), 图1 定理1中系统的误差曲线Fig.1 The systems errors of theorem1 文中基于Lyapunov稳定性理论和分数阶微积分利用自适应滑模方法研究了分数阶Duffling系统的一种新型趋近律的自适应滑模同步问题,研究表明:设计适当的滑模函数和控制器可以实现主从系统滑模混沌同步。同时,仿真算例也表明了方法的有效性. [1]MANDELBROTBB,vanNESSJW.FractionalBrownianmotions,fractionalnoisesandapplications[J].SiamReview,1968,10(4):422-437. [2]MANDELBROTBB,Thefractalgeometryofnature[M].NewYork:W.H.Freeman&CoLtd,1974. [3]SHAHIRIM,GHADRIR,RANJBARN,etal.Chaoticfractional-ordercoulletsystem:synchronizationandcontrolapproach[J].CommunNonlinearSciNumericalSimulation, 2010,15(3):665-674. [4]HAMAMCISE,KOLKSALM.Calculationofallstabilizingfractional-orderPDcontrollersforintegratingtimedelaysystems[J].ComputationMathematicsApplication,2010,15(4):1267-1278. [5]MATOUKA.Chaosfeedbackandsynchronizationoffractional-ordermodifiedautonomousVanderpol-Dufflingcircuit[J].CommunNonlinearSciNumericalSimulation,2011,16(2):975-986. [6] 丁金凤,张毅. 基于按指数律拓展的分数阶积分的El-Nabulsi-Pfaff变分问题的Noether对称性[J].中山大学学报(自然科学版),2014,54(6):150-154. DINGJinfeng,ZHANGYi.NeothersymmetriesforEl-Nabulsi-Pfaffvariationalproblemforextendedexponentialfractionalintegral[J].ActaScientiarumNaturaliumUniversitatisSunyatseni,2014,53(6):150-154. [7]MOHADESZADEHM,DELAVARIH.Synchro-nizationoffractionalorderhyper-chaoticsystemsbasedonanewadaptiveslidingmodecontrol[J].IntJDynamControl,2015,10(7):435-446. [8]DELAVARIH,GHADERIR,RANJBARA,etal.Fuzzyfractionalorderslidingmodecontrollerfornonlinearsystems[J].CommunicationsinNonlinearScienceandNumericalSimulation, 2010, 15 (4):963-978. [9] 毛北行, 李巧利. 一类分数阶Genesio-Tesi系统的滑模混沌同步[J]. 中山大学学报(自然科学版),2017,56(2):76-79.MAOBeixing,LIQiaoli.SlingmodechaossynchronizationofaclassoffractionalorderGenesio-Tesisystems[J].ActaScientiarumNaturaliumUniversitatisSunyatseni,2017,56(2):76-79. [10]DADRASS,MOMENIHR.Fractionalterminalslidingmodecontroldesignforaclassofdynamicalsystemswithuncertainty[J].CommunicationsinNonlinearScienceandNumericalSimulation, 2012,17(1):367-377. [11] 徐瑞萍,高明美. 自适应终端滑模控制不确定混沌系统的同步[J].控制工程,2016,23(5):715-719.XURuiping,GAOMingmei.Synchronizationofchaoticsusyemswithuncertaintyusingadaptiveterminalslidingmodecontroller[J].ControlEngineeringofChina, 2016, 23(5):715-719. [12] 周涛. 基于一种新型趋近律的自适应滑模控制[J]. 控制与决策,2016,31(7):1335-1338.ZHOUTao.Adaptiveslidingcontrolbasedonanewreachinglaw[J].ControlandDecision,2016, 31(7): 1335-1338. [13]PODLUBNY.Fractionaldifferentialequation[M].SanDiego,CA,USA:AcademicPress, 1999:715-719. [14] 梅生伟,申铁龙,刘志康.现代鲁棒控制理论与应用[M]. 北京: 清华大学出版社, 2003. Self-adaptive sliding mode synchronization of fractional-order uncertainty Duffling systems based on a new reaching law MAO Beixing (College of Science, Zhengzhou University of Aeronautics, Zhengzhou 450015, China) The problem of self-adaptive sliding mode chaos synchronization of fractional-order uncertainty duffling systems based on a new reaching law is studied in the paper. The sliding mode functions and controllers are given out using self-adaptive sliding mode approach and got the sufficient conditions for the master-slave systems getting sliding mode synchronization . It is proved that master-slave systems are sliding model chaos synchronization under proper controllers and sliding mode surface. The strict deduce and proof in mathematics are given out in the paper. Numerical simulations examples of chaotic system verify the effectiveness of the proposed method. fractional-order Duffling systems; self-adaptive sliding mode ;chaos synchronization 10.13471/j.cnki.acta.snus.2017.04.011 2017-03-11 基金项目:国家自然科学青年基金(NSFC11501525);河南省高等学校青年骨干教师资助计划项目(2013GGJS-142) 毛北行 (1976年生),男;研究方向:复杂网络与混沌同步;E-mail:bxmao329@163.com O482.4 A 0529-6579(2017)04-0064-04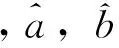
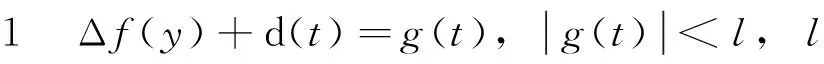
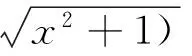
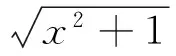
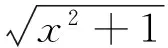
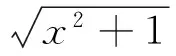
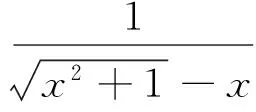
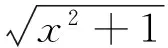

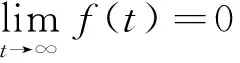
3 主要结果
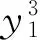
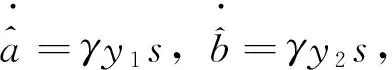
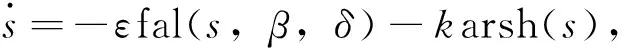

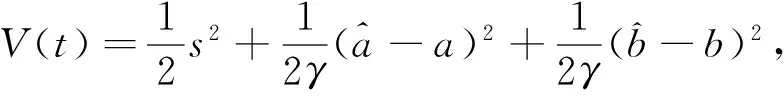

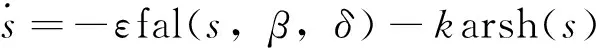
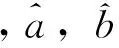
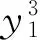
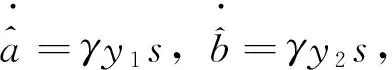
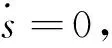
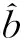
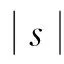
4 数值仿真
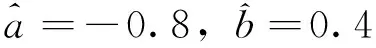
5 结 论

