轮胎带束层结构变化对固有频率的影响研究
朱新静,朱作勇,赵鹏翔,冯希金
(赛轮金宇集团股份有限公司,山东 青岛 266045)
轮胎是汽车与地面接触的唯一部件,它的动力学特性影响汽车的动力性、经济性、操纵稳定性和噪声。
研究轮胎在各种复杂激励下的振动和噪声响应特性,首先要研究轮胎的固有频率和模态特性,常用的研究方法有试验方法[1-3]、解析方法和有限元分析方法[4-5]。
本研究基于Abaqus非线性有限元分析软件建立三维轮胎的振动模态分析方法,求出轮胎径向各阶振型,并进行实际轮胎的振动模态试验,分析轮胎结构带束层方案改变对轮胎固有频率的影响规律,以期为后续整车配套过程中遇到的振动和舒适性问题提供解决思路。
1 轮胎固有频率和模态的有限元求解方法
1.1 动力学系统的有限元求解方程
根据动力学系统的基本理论,求解动力学响应的基本方程为

如果忽略阻尼的影响,则运动方程简化为
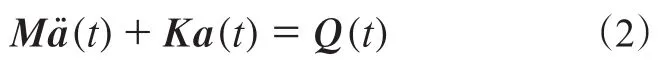
若运动方程(2)的右端项为零,则可以进一步简化为
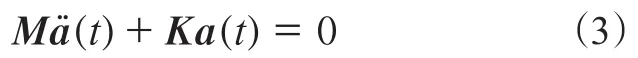
运动方程(3)为系统的自由振动方程,可以求解出系统的无阻尼固有频率和模态。
运动方程(1)的求解方法有直接积分法和振型叠加法,考虑到计算成本和计算效率,通常采用振型叠加法。振型叠加法的基本思路是先求解系统的自由振动方程(3),得到系统的无阻尼固有频率和固有振型,然后用固有振型对运动方程(1)进行交换,最后对各自由度的运动方程进行积分并叠加,从而求得。
1.2 固有频率和模态的有限元求解方法
运动方程(3)的求解有4种方法:矩阵反迭代法、子空间迭代法、Ritz向量直接叠加法和Lanczos向量直接叠加法。矩阵反迭代法算法简单,比较适合求解数目较少的特征值的情况,子空间迭代法是将矩阵反迭代法推广应用于同时利用若干个向量进行迭代的情况,即用于求解更多特征值的情况。而Ritz向量直接叠加法和Lanczos向量直接叠加法的共同特点是直接生成一组Ritz向量或者Lanczos向量,对运动方程进行缩减,然后通过求解缩减的运动方程的特征值问题,进而得到原系统的特征解,从而避免了矩阵反迭代法和子空间迭代法的迭代步骤,具有更高的计算效率。本研究采用的是Lanczos向量直接叠加法。
1.3 轮胎有限元模型
建立205/55R16光面轮胎动力学有限元模型。轮胎二维有限元模型如图1所示,将二维模型进行周向旋转形成如图2所示的三维有限元模型。

图1 轮胎二维有限元模型

图2 轮胎三维有限元模型
采用标准轮辋,充气压力为250 kPa,轮胎负荷为零。
单元格类型设定为减缩积分模式,即四角形单元设定为CGAX4R,三角形单元设定为CGAX3。橡胶材料属性定义为Neo-Hooke模型,帘线材料属性定义为线弹性模型。
1.4 径向振动模态仿真结果
轮胎的振动行为较复杂,从其宏观的振动形态来看,大体可以分为径向振动模态、横向振动模态和周向振动模态,本工作主要针对径向振动模态进行研究。
径向振动模态是轮胎振动的主要形式之一,反映了轮胎在不同振动频率下的径向变形,与车辆的乘坐舒适性有很大关系。径向各阶振动模态的仿真结果如图3所示。
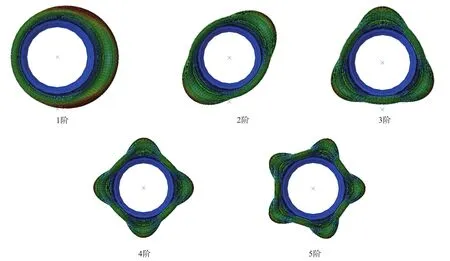
图3 径向各阶振动模态的仿真结果
2 轮胎固有频率和模态的试验方法
2.1 振动模态试验装置
为了验证有限元分析结果,进行轮胎振动模态的测量试验。轮胎振动模态试验装置如图4所示。

图4 轮胎振动模态试验装置
试验采用单点激振、两点响应测振的方式。在轮胎的中心圆周上均匀设置24个测振位置,试验过程中通过移动力锤的方法实现对这24个位置振动信号的测量。本次试验采用单向加速度传感器,每次试验可提取单一方向的加速度信号,根据更换传感器的位置获得径向模态和横向模态。
振动模态试验装置通常自带信号处理软件,可以直接得到各阶固有频率。
2.2 径向振动模态试验结果
径向各阶振动模态的试验结果如图5所示。
从图5可以看出,仿真计算结果与试验结果吻合。

图5 径向各阶振动模态试验结果
2.3 不同带束层结构的轮胎方案
为了研究不同带束层结构对轮胎固有频率的影响,选取205/55R16光面轮胎,改变轮胎带束层的材质、角度和宽度,采用仿真方法和室内测试方法分析轮胎带束层对轮胎固有频率的影响规律,并对照仿真与室内测试的结果,完善仿真方法,为后续研发预测奠定基础。
表1列出了此次的所有设计方案,包括钢丝材质、带束层宽度及带束层角度。对比方案如下。

表1 轮胎设计方案汇总
(1)带束层材质对固有频率的影响:1#—4#综合对比;
(2)带束层角度对固有频率的影响:3#,5#和6#综合对比;
(3)带束层宽度对固有频率的影响:3#,7#—9#综合对比。
3 结果与讨论
3.1 带束层材质对固有频率的影响
表2示出了4种不同带束层材质轮胎的固有频率模拟仿真计算结果和试验结果。
其中,4种材质的弹性模量(E)数据对比为EA=EB<EC<ED;4种材质的单根面积数据对比为EA=EB<EC<ED;4种材质的单丝密度(EPI)数据对比为EC=ED<EA<EB。
由表2可以看出,D材质的试验结果和仿真结果固有频率均低于其他3种材质。
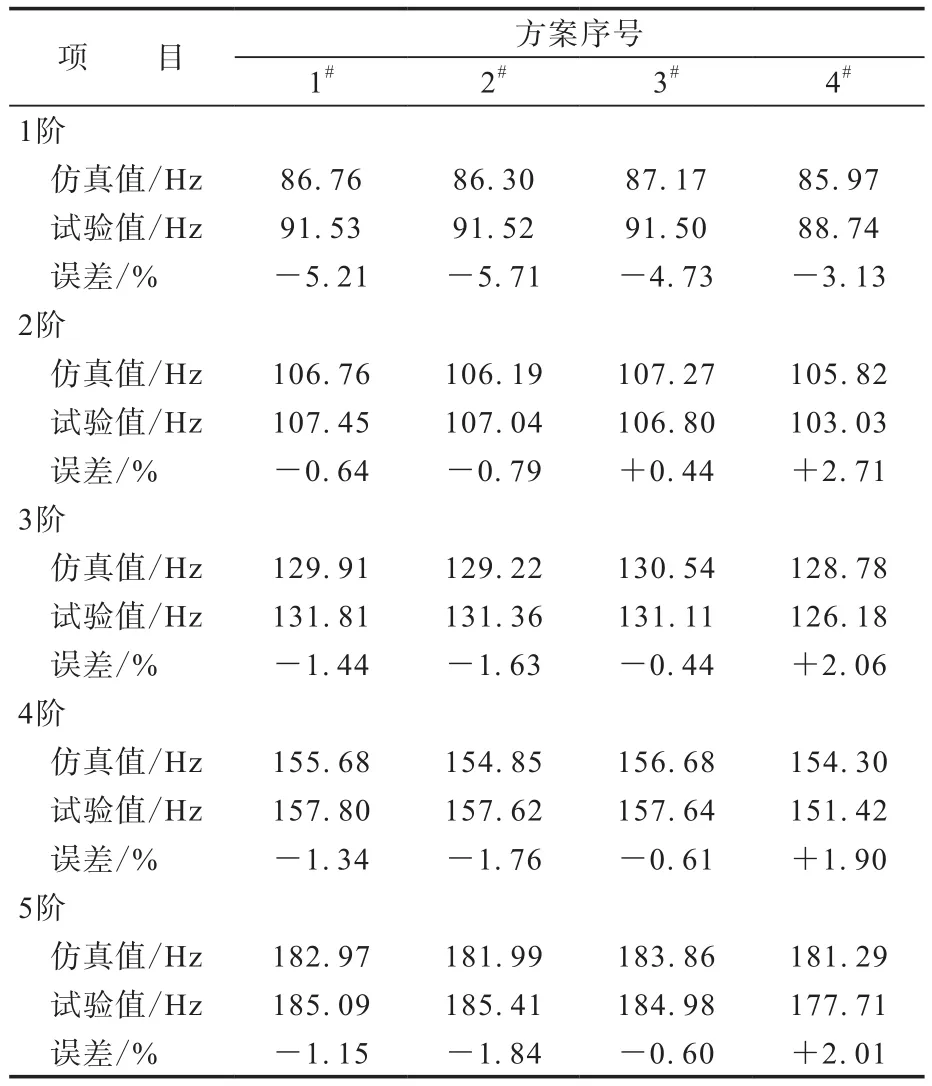
表2 不同带束层材质轮胎的固有频率试验和仿真结果
4种材质的仿真结果与试验结果趋势基本一致,1阶固有频率计算误差约为5%,2阶以上小于4%。试验结果差异不明显,但试验结果影响因素较多,而仿真结果受影响较小,更能反映材料对固有频率的影响趋势。
3.2 带束层角度对固有频率的影响
表3示出了3种不同带束层角度轮胎的固有频率模拟仿真计算结果和试验结果。
从表3可以看出,1阶仿真结果与试验的误差小于5%,2阶误差小于3%,3—5阶误差小于1.5%。
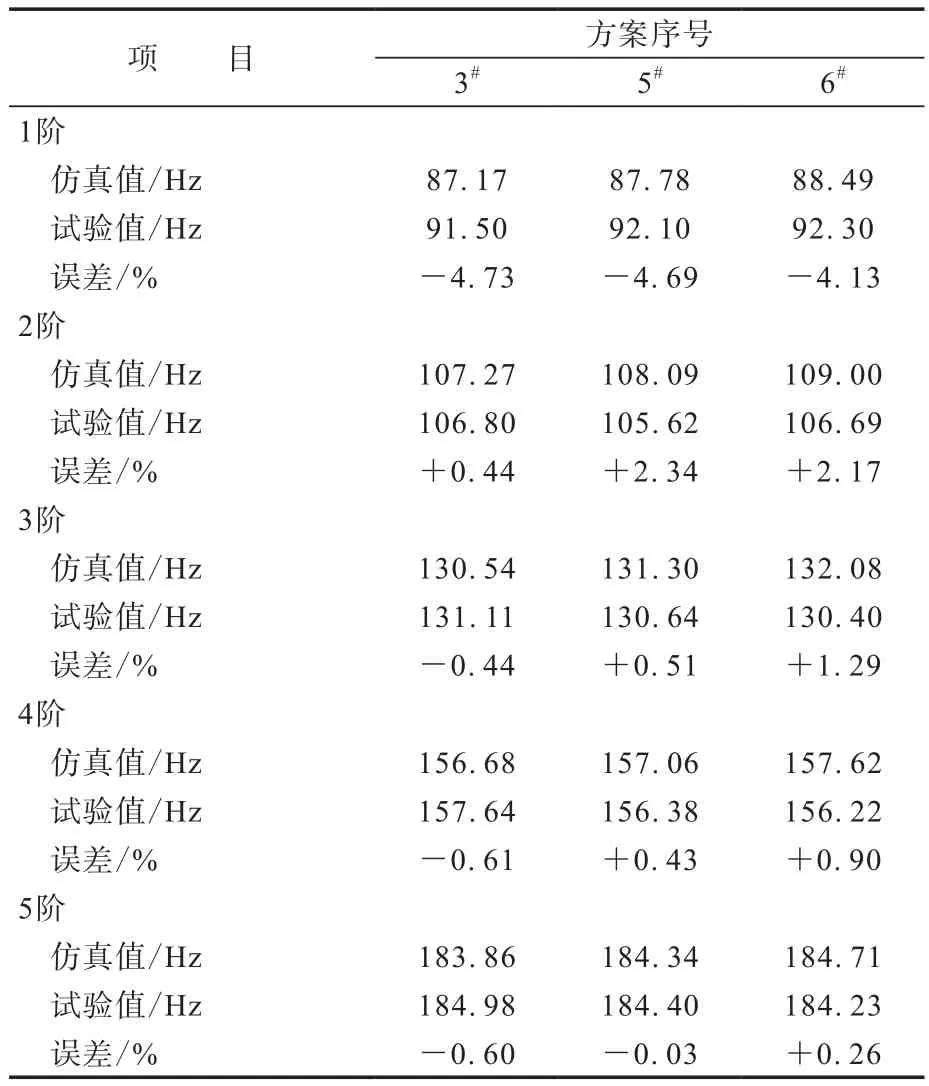
表3 不同带束层角度轮胎的固有频率试验和仿真结果
当带束层角度由27°变化为21°时,不同方案各阶固有频率的仿真计算值差别不大,约为1 Hz。而从试验结果来看,误差均小于1 Hz,因此可以判定,带束层角度改变对轮胎的固有频率影响较小。
3.3 带束层宽度对固有频率的影响
表4示出了4种不同带束层宽度轮胎的固有频率的模拟仿真计算结果和试验结果。带束层宽度关系为:8#<7#<3#<9#。
由表4可以看出,1阶仿真结果与试验结果误差小于5%,2阶误差小于3%,3—5阶误差小于2%。
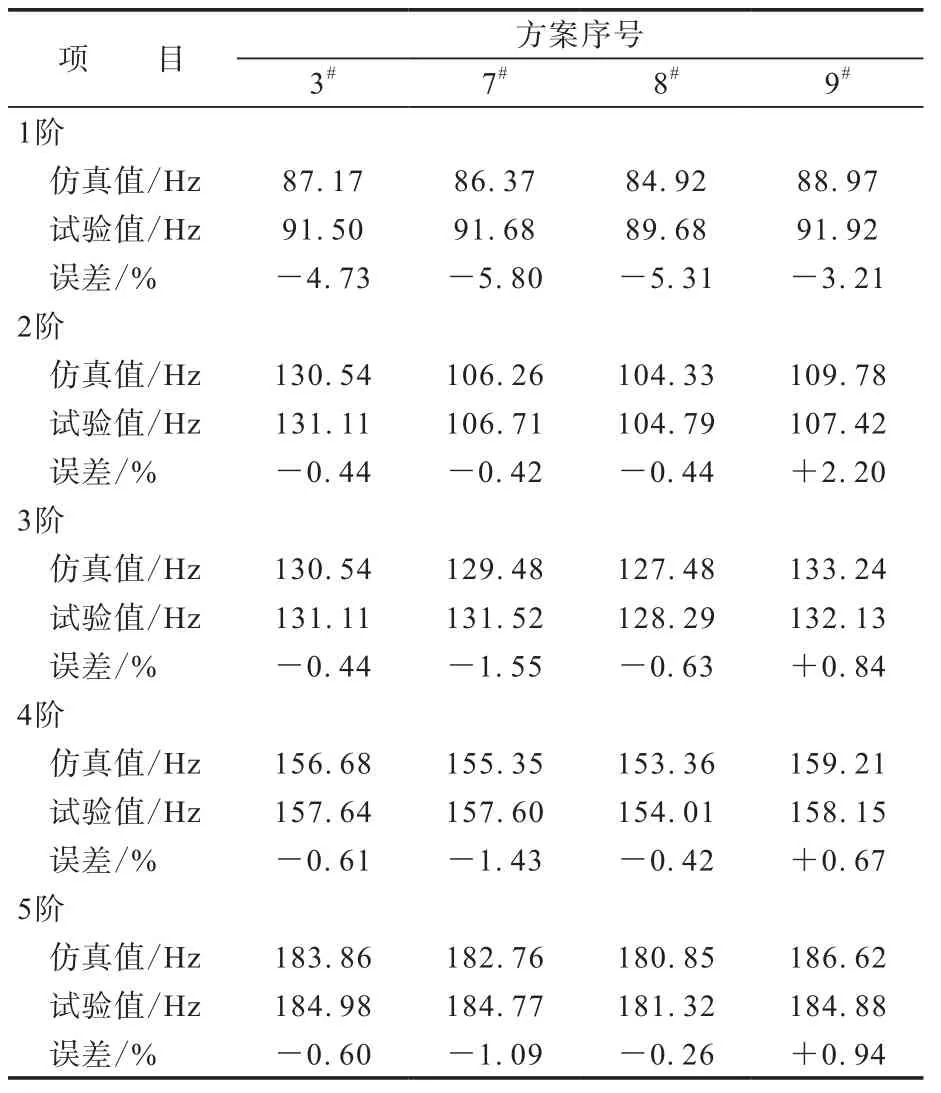
表4 不同带束层宽度轮胎的固有频率试验和仿真结果
每一阶次下,随着带束层宽度的增加,固有频率提高,最窄带束层方案与最宽带束层方案差异值为2~5 Hz,随着阶次增加,差异明显。
4 固有频率和模态测试的影响因素
4.1 轮辋材质
针对5#方案中进行了锻铝轮辋及钢制轮辋的测试对比,对比结果见表5。
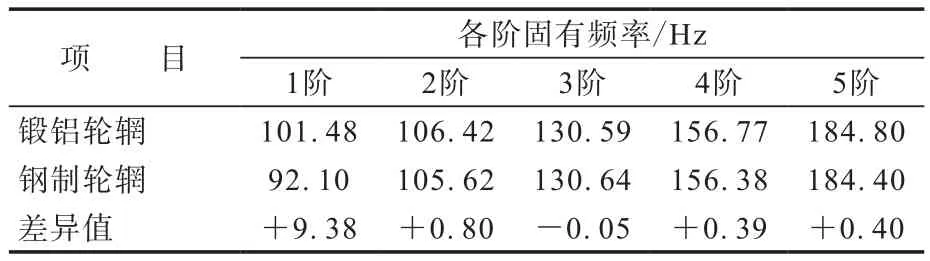
表5 轮辋对固有频率测试的影响对比
由表5可以看出,轮辋对1阶测试结果影响较大,锻铝轮辋测试结果较钢制轮辋测试结果高约10 Hz,2—5阶结果差异小于1 Hz。
4.2 轮辋约束条件
目前试验室内模态测试采用的约束条件分为自由条件及固定条件两种,本工作分别对两种约束条件进行对比测试,测试结果见表6。
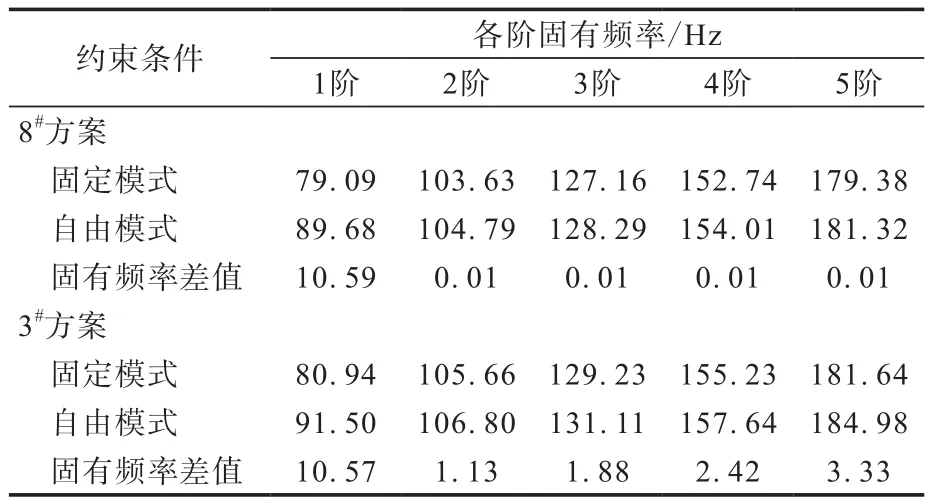
表6 约束条件对固有频率的影响对比
由表6可以看出,自由及固定两种约束条件主要影响1阶模态固有频率,自由状态下的固有频率比固定状态下的高约10 Hz,2—5阶模态比固有频率高0~3 Hz。
5 结论
本工作开发了轮胎固有频率和模态的有限元仿真技术,进行了不同带束层结构的多个方案固有频率和模态的仿真计算及试验,结论如下。
(1)轮胎的固有频率和模态的仿真计算结果和试验结果非常接近,两者误差小于5%,尤其是2阶以上的误差小于4%,因此有限元方法是可靠的。
(2)在21°,24°和27°范围内,带束层角度对径向振动固有频率影响较小。
(3)带束层宽度和帘线种类对固有频率有一定影响。
(4)测试轮辋类型和约束方式对固有频率影响较大,对其他阶的固有频率影响不大。

