浅谈极限的几何意义在高等数学教学中的运用

刘琼玲++王林林

【摘要】极限是高等数学的核心内容之一，对极限定义的理解常常是高等数学教学的难点.本文从数列极限的几何意义入手，借助几何意义的直观性来理解极限的定义，详细分析了极限的有界性、唯一性、保号性等重要性质，并举例说明了如何从几何意义的角度寻找部分问题的解题思路.

【关键词】极限；几何意义；数列

【基金项目】国家自然科学基金（11501561）；中国矿业大学基本科研业务费项目（2014QNA58）.

一、引言

极限思想贯穿整个高等数学始终，是高等数学学习的基础，高等数学中的许多概念及运算法则都是建立在极限的基础之上，因此，在高等数学教学中，使学生充分理解极限的定义、内涵和性质等是十分必要的.而通过几何意义体现出的生动活泼的极限思想，能够提高学生的学习兴趣，加深学生对极限本质的认识，使得这一概念不再仅仅是一种形式化的表达.

在教学过程中，首先，从几何意义的角度给出直观的几何解释，提起学生的学习兴趣，使得学生对概念或性质等有个直观的印象和初步的理解，然后，进行严格的理论推导，可使学生理解起来相对容易，更加容易掌握定义和性质的内涵，会收到较好的教学效果.

二、数列极限的定义和几何意义

（一）定义（ε-N语言）[1]

对于数列{xn}及常数a，ε>0（无论多么小），总存在正整数N，当n>N时，恒有|xn-a|<ε，则称a是{xn}的极限，或称{xn}收敛于a，记作

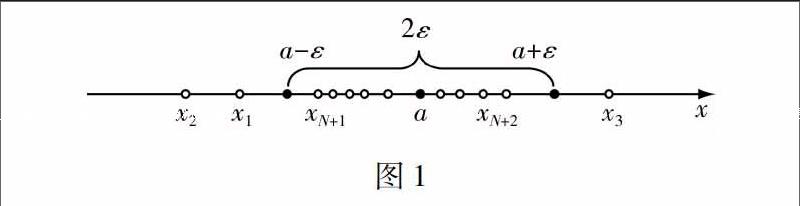
（二）几何意义

在定义中|xn-a|<εa-ε0，可以找到一个正整数N，只要n>N，所有xn都落在开区间（a-ε，a+ε）内，只有有限项（至多N项）在这个区间外面（如图1）[2].

随着n的增大，xn代表的点越来越“密集”在点a的附近.

结合数列的几何意义可以更加有效地向学生讲解数列极限的有界性、唯一性、保号性以及数列子列的收敛性等性质.

三、从几何意义的角度理解数列极限的性质

（一）有界性：如果数列{xn}收敛，则数列{xn}一定有界

分析设 limn→∞xn=a，根据上述几何意义，对于任一给定的正数ε，一定都有正整数N，数列{xn}从第N+1项开始都落在区间（a-ε，a+ε）里面，不妨取ε=1，那么{xn}从某一项开始都落在区间（a-1，a+1）里面，剩下的有限项自然是有界的，取一个既包含区间（a-1，a+1）又包含剩下的有限多项的闭区间[-M，M]即可证明结论成立.

（二）唯一性：如果数列{xn}收敛，则极限唯一

（四）数列子列的收敛性：如果数列{xn}收敛于a，则它的任一子列{xnk}都收敛于a

分析设 limn→∞xn=a，根据极限的几何意义，对于任一给定的正数ε，都存在正整数N，数列{xn}从第N+1项开始都落在區间（a-ε，a+ε）里面，在区间（a-ε，a+ε）外面只有数列{xn}中的有限项，而{xnk}作为{xn}的子列，自然也只有有限项落在区间（a-ε，a+ε）外面，于是可以找到正整数N*，使得{xnk}从第N*+1项开始都落在区间（a-ε，a+ε）里面，这就说明{xnk}同样收敛于a.

对于函数f（x）的极限，可以类似地讨论其几何意义并从几何意义的角度分析其性质，这里就不再累述.

四、运用几何意义分析问题并寻找证题思路

部分关于极限的证明题，同样可以从几何意义的角度来理解，从而找到解决问题的正确思路.

分析因为 limk→∞x2k-1=a且 limk→∞x2k=a，根据几何意义可知，对于任一给定的正数ε，可以找到共同的正整数N，数列{x2k-1}和{x2k}均从第N+1项开始都落在区间（a-ε，a+ε）里面，在区间（a-ε，a+ε）外面只有{x2k-1}和{x2k}中的有限项，因此，在区间（a-ε，a+ε）外面必然只有数列{xn}中的有限项，这就说明了{xn}也是收敛于a.

在高等数学中，类似的问题还有很多，例如，导数[3]、微分中值定理、定积分等等，均有其几何意义，从几何直观出发对相应的问题进行分析可以加深对概念或问题内涵的理解，使得抽象复杂的数学问题变得形象直观，在教学中合理运用这些几何意义，不仅能够使得教师的教学活动事半功倍，更能提高学生分析问题和解决问题的能力.

【参考文献】

[1]同济大学数学系.高等数学：上册[M].北京：高等教育出版社，2007.

[2]张兴永，杨宏晨，吴宗翔，逄世友，赵迁贵.高等数学：上册[M].北京：煤炭工业出版社，2014.

[3]王芳，汪晓勤.HPM视角下“导数几何意义”的教学[J].数学教育学报，2012，21（05）：57-60.