三维角联锁机织复合材料的冲击破坏有限元模拟分析

马 倩，王 可，金利民

(1. 盐城工业职业技术学院 纺织服装学院，江苏 盐城 224005；2. 中国科学院 上海应用物理研究所，上海 201204；3. 东华大学 纺织学院，上海 201620；4. 武汉纺织大学 湖北省纺织新材料及其应用重点实验室，湖北 武汉 430200)



三维角联锁机织复合材料的冲击破坏有限元模拟分析

马 倩1，王 可1，金利民2，3，4

(1. 盐城工业职业技术学院 纺织服装学院，江苏 盐城 224005；2. 中国科学院 上海应用物理研究所，上海 201204；3. 东华大学 纺织学院，上海 201620；4. 武汉纺织大学 湖北省纺织新材料及其应用重点实验室，湖北 武汉 430200)

为研究层层接结三维角联锁机织复合材料的抗高速冲击性能，以指导抗冲击材料的结构设计，通过有限元分析的方法，计算此材料在具有不同入射速度弹体冲击下的动态响应。通过对比各种冲击条件下弹体的速度与时间曲线、加速度与时间曲线、材料渐进破坏扩展及最终破坏形态等的结果发现：冲击过程中，弹体的速度变化可被划分成2个阶段；弹体的加速度波动情况可直接反映复合材料靶体吸收弹体动能的动态规律；此外，经纱发生波浪状屈曲的区域是该类材料的重要结构部位，应在设计抗冲击型三维角联锁机织复合材料时进行局部强化与结构优化。

三维角联锁；复合材料；高速冲击；有限元分析

目前，具有质量轻、强度高、力学性能突出等一系列优点的三维纺织结构复合材料已得到日益广泛的研究与应用[1-3]。其中，三维角联锁机织复合材料也因其较为显著的力学性能优势，得到了越来越多的关注。

在三维角联锁机织结构中，通过经纱与纬纱这2个纱线系统的相互缠绕和交织，形成了稳定而坚固的织物结构。根据经、纬交织层数的不同种类，又可进一步地细化为层层接结、贯穿接结2种角联锁机织结构，分别被赋予了各自的性能与优势[4-5]，且可在工程实际应用中根据需要来研究经纬纱的排列规律，设计不同的三维角联锁组织结构，以适应特定的工程应用条件，体现了该种织物的结构多样化与多功能性[6-8]。在这种情况下，以三维角联锁机织物作为复合材料的增强相，同时以高性能树脂作为复合材料的基体相制作而成的复合材料则自然具有了很好的力学性能，在各种力学工况中都显示出较为突出的优势[9-11]。鉴于三维角联锁机织复合材料的抗分层能力，其也被广泛地应用于抗冲击领域，通过考察这类材料在高速冲击载荷条件下的破坏与吸能行为，进而优化设计可应用于抗高速冲击领域的复合材料结构[12-14]。尽管如此，现有文献中对三维角联锁机织复合材料在高速冲击条件下破坏机制的阐述仍不够完善与深入。

本文运用有限元分析的方法，在“纱线-树脂”尺度的细观结构模型上计算一种层层接结三维角联锁机织复合材料在具有不同初始速度(500、600、800 m/s)弹体的冲击下的破坏行为。对比分析以上3种不同冲击速度情况下弹速的变化历程、弹体加速度的变化历程、材料渐进破坏扩展过程以及材料最终的破坏形态等指标，阐述此类结构材料的抗高速冲击力学行为，以期为抗冲击三维角联锁机织复合材料的结构优化与设计提供指导。

1 材料与模型

1.1 材 料

本文研究的复合材料由层层接结三维角联锁机织物增强体与不饱和聚酯树脂基体所构成。选用的三维角联锁机织物由南京玻璃纤维研究院提供，基体是由亚什兰复合材料聚合物集团生产的一种热固性树脂，即聚酯树酯AROPOLTMINF 80501-50。增强体、基体以及弹体的材料规格见表1。

表1 增强体、基体与弹体的材料规格Tab.1 Specifications of reinforcement, matrix and projectile

图1为复合材料的结构示意图。作为复合材料增强相的三维角联锁机织结构由经纱和纬纱构成。纬纱平行排列，经纱则沿着材料的厚度方向衬入，形成对材料整体的束缚作用，从而保证结构的稳定性。再经由树脂基体的固化作用，形成坚固的复合材料结构。

图1 层层接结三维角联锁机织复合材料的细观模型图Fig.1 Micro-structural model of layer-to-layer 3-D angle-interlock woven composite

1.2 有限元模型

通过ABAQUS有限元分析软件，Windows XP 32位版本操作系统，建立三维角联锁机织复合材料与球形弹体冲击系统的有限元模型，如图2所示。模型中，3种冲击条件下的弹体初始速度分别为500、600、800 m/s，复合材料的左、右两端面被完全固定(见图2(a))。系统的网格化结果如图2(b)所示，网格的划分原则主要是考虑其对有限元计算结果精确性的影响。根据模型大小合理确定网格格距，特别是在形状不太规则的复合材料树脂基体的短边、尖锐的边角等处划分较多较细的网格，以此保证网格的合理精细度以及计算的精度。

模型中的各部件性能参数设置中，织物增强体、树脂基体以及弹体的参数列于表1。由于本文研究所关注的主要分析对象为复合材料靶体，故将弹体设为在冲击过程前后无任何变形的刚体。

图2 三维角联锁机织复合材料冲击系统的有限元模型Fig.2 Finite element model for impact system of 3-D angle-interlock woven composite. (a) Impact system; (b) Mesh scheme

2 结果与讨论

2.1 速度与时间关系曲线

图3 弹体速度与时间关系曲线Fig.3 Velocity vs. time curves. (a) Different impact velocity; (b) Part of curve at 500 m/s impact velocity

图3示出各种不同冲击情况下的弹速与时间关系曲线。从图中可看出，弹体在冲击过程中，其速度的变化可划分为2个阶段。

第1阶段：弹速急降阶段。弹体与复合材料表面发生接触的瞬间至弹体贯穿材料(初始弹速较大时，800 m/s与600 m/s)，或未能击穿，弹体速度降为0而被靶体捕获(初始弹速较小时，即500 m/s)，当弹体与复合材料表面发生侵彻作用后，材料即进入破坏阶段。此刻，冲击应力波沿树脂以及经、纬2个系统纱线的延伸方向上以一定的应力波速在材料内部迅速扩展，从而将高速冲击载荷迅速传递到复合材料靶体的整体结构。应力波速根据下式计算[15]。

式中：c为应力波在介质中的传播速度；E为高应变率下介质的弹性模量；ρ为介质的密度。

当弹体逐步侵彻至织物增强体后，由于在弹体前进的路径上分布着一定数量的纱线增强体，使得弹体所受阻力也急剧加大。当各纱线达到最大断裂强度后即发生断裂失效，进而吸收大量的弹体动能。以上因素导致弹速急剧下降。

第2阶段：弹速平稳阶段。此阶段中，对于初始弹速足够大(800、600 m/s)的情况，由于弹体的初始动能较大，令其可击穿复合材料靶体并且以一定的剩余速度(800、600 m/s初始弹速时，剩余速度分别为163.2、1.8 m/s)射出。因弹体不再受其他任何外在作用力，故其速度保持平稳。当弹体的速度不够大(500 m/s)时发现，弹体的速度下降为0后，即因弹体的初始动能较小而未能击穿复合材料靶体，反而被靶体所捕获。此时，由于复合材料靶体具有一定的弹性回复效应，故而反弹弹体使之在复合材料靶体内部发生持续一段时间的小幅度振动(见图3(b))。

2.2 加速度与时间关系曲线

弹体的加速度变化规律可直观反映侵彻过程中其承受复合材料靶体反作用力的变化情况。图4示出各冲击情况下弹体的加速度与时间关系曲线。

图4 弹体加速度与时间关系曲线Fig.4 Acceleration-time curves

从图4中可看出，对应于不同的初始弹速，加速度曲线皆出现了类似的屈曲波动现象。出现如此波动现象的原因是：一方面，由于高速冲击情况下，三维角联锁机织复合材料靶板耗散、吸收冲击能量的主要表现是树脂基体与纤维增强体的开裂及断裂失效。当二者因高能冲击作用达到各自的失效阈值而破坏时，即对弹体造成较大的阻力，从而在加速度曲线图上出现了对应的峰值。实际情况中，在弹体侵彻复合材料的过程中，连续不断地发生弹体与树脂基体、弹体与纤维增强体的相互作用，树脂基体与纤维增强体皆发生了连续的破坏与断裂失效，从而使得加速度曲线图上出现一连串的峰值；另一方面，相比于树脂基体，纱线增强体的力学性能明显更好，可吸收更多的冲击能量，因而是复合材料的主要承力组分，故当弹体侵彻纱线部分时会承受较大的阻力，当纱线达到最大失效强力而发生断裂时，此时弹体所受的阻力最大，其加速度也随之出现更为明显的峰值。

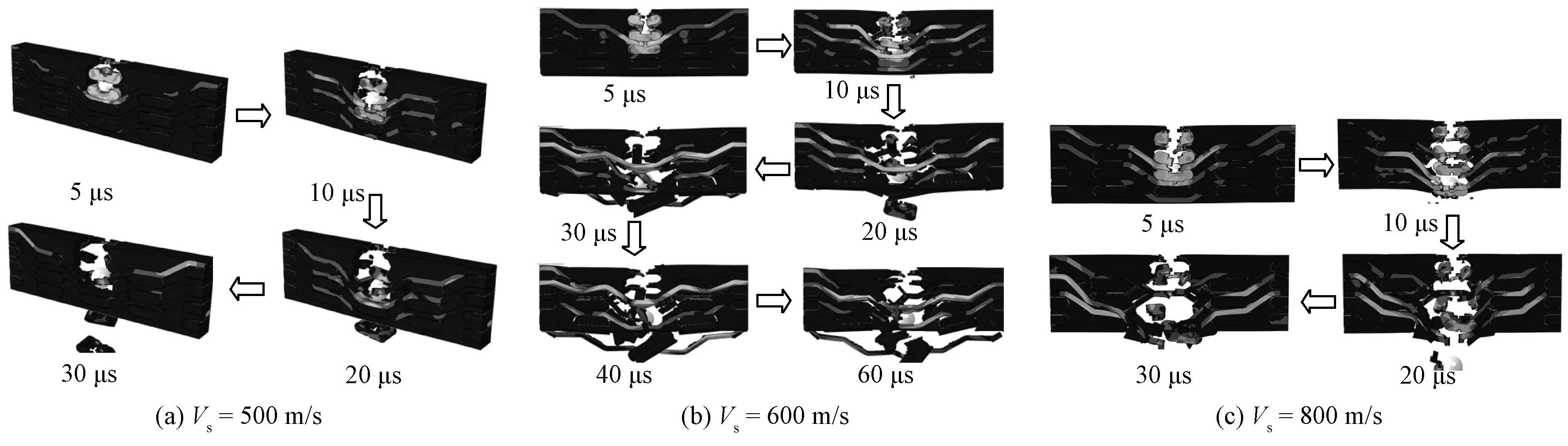
图5 材料渐进破坏形态Fig.5 Progressive damage morphologies of composite subjected to impact loading

图6 复合材料冲击破坏形态Fig.6 Damage morphology of composite undergoing impact loading. (a) Surface; (b) Cross-section

此外在图4中还可发现，弹体初始速度越大，其加速度峰值也越大。这是由于弹体速度越高，其在单位时间内侵彻的基体或增强体的量也越大，得到的反作用力也就越强烈，故加速度峰值也越大。

2.3 破坏形态

为说明三维角联锁机织复合材料在高速冲击下的结构破坏机制，以有利于抗冲击复合材料的结构优化设计，有必要考察复合材料靶体的渐进破坏扩展的情况。图5示出复合材料在不同冲击情况下，不同冲击时刻点的破坏形态。

从图5可看出，对于三维角联锁机织复合材料，树脂与纤维的开裂、纤维的抽拔与断裂为其主要的破坏模式。此外，弹体冲击轨迹上的材料破坏特别剧烈，应力波主要是沿着纱线的延伸方向，尤其是沿着经纱的长度方向传播，且以较高的速度向材料结构的其他区域扩散，从而有利于复合材料的整体承力，如图6所示。

此现象与文献[16]所描述的具有相似经纬纱交织结构的三维角联锁机织复合材料的弹道冲击破坏模式一致。

为探究材料在高速冲击下的关键结构区域，以便于抗冲击材料的结构优化设计，图7示出三维角联锁机织复合材料在不同弹速下的最终破坏形态。从图中可清楚观察到非直接受弹体冲击区域的裂纹(图中箭头指示处)。这些区域都位于靠近经纱上发生波浪状屈曲部位的基体上。由此可推断，由于应力波主要是沿着经纱的长度方向进一步扩展，此外还鉴于此结构类型材料的应力集中效应，最易发生开裂破坏的区域即位于上述各部位，故在设计抗冲击三维角联锁机织复合材料时，应特别注重此类效应，可采用局部加强或结构优化的方法来强化材料的力学性能。

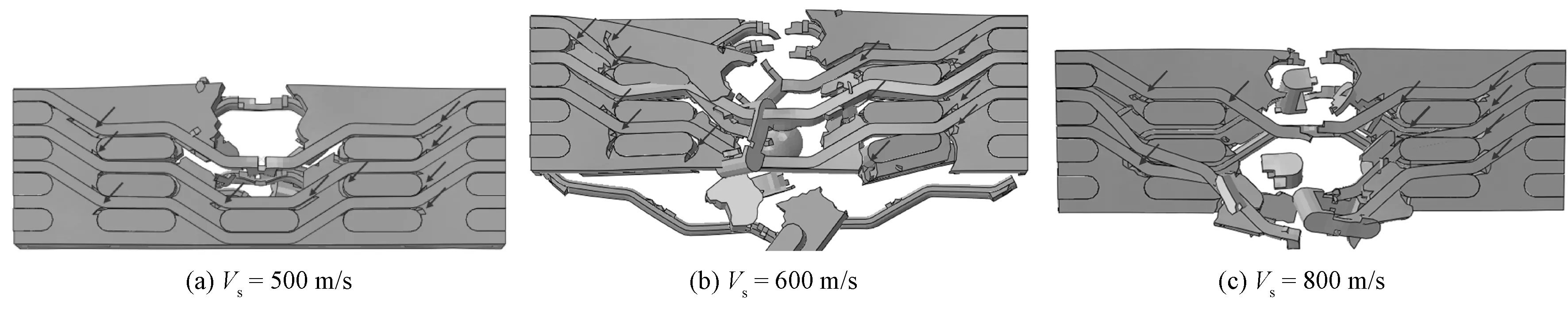
图7 最终破坏形态Fig.7 Ultimate damage morphology of composite

3 结 论

1)三维角联锁机织复合材料在高速冲击过程中，弹体速度的变化主要经历2个阶段，即弹速急降阶段与弹速平稳阶段，由冲击过程中树脂与增强体的破坏规律所决定。

2)弹体加速度的波动规律是弹体承受靶体反作用力的直接体现，因此可直接反映靶体的吸能与破坏规律。

3)对于三维角联锁机织复合材料，树脂与纤维的开裂、纤维抽拔与断裂为其主要的破坏模式。此外，应力波主要是沿着经纱的长度方向传播，以较高的速度向材料结构的其他区域扩散，从而有利于复合材料的整体承力。

4)经纱发生波浪状屈曲的区域是三维角联锁机织复合材料的重要结构部位。在设计抗冲击三维角联锁机织复合材料时，应特别注重这点，可采用局部加强或结构优化的方法强化材料的性能。

FZXB

[1] MOURITZ A P, BANNISTER M K, FALZON P J , et al. Review of applications for advanced three-dimensional fibre textile composites[J]. Composites Part A, 1999, 30: 1445-1461.

[2] MIRAVETE A. 3-D Textile Reinforcements in Composite Materials[M]. Cambridge: Woodhead Publishing Limited, 1999: 9-65.

[3] HU J, JIANG Y. Modeling formability of multiaxial warp knitted fabrics on a hemisphere[J]. Composites Part A, 2002, 33(5): 725-734.

[4] TONG L, MOURITZ A P, BANNISTER M K. 3D Fiber Reinforced Polymer Composites[M]. Boston: Elsevier Science Ltd, 2002: 1-12.

[5] 金利民. 三维角联锁机织复合材料三点弯曲疲劳性能与结构效应[D]. 上海：东华大学, 2012: 1-3. JIN Limin. Fatigue behavior and structural effects of 3-D angle-interlock woven composites undergoing three-point bending cyclic loading[D]. Shanghai: Donghua University, 2012: 1-3.

[6] 聂建斌, 卢士艳. 角联锁织物的组织设计[J]. 纺织学报, 2006, 27(3): 90-91. NIE Jianbin, LU Shiyan. Construction of angle-interlock woven fabric[J]. Journal of Textile Research, 2006, 27(3): 90-91.

[7] 白燕. 正则多重纬角联锁机织物的快速设计[J]. 纺织学报, 2013, 34(2)：61-64. BAI Yan. Rapid design of regular multiple weft angle interlocking fabric[J]. Journal of Textile Research, 2013, 34(2): 61-64.

[8] 许鹤, 唐予远, 马菲, 等. 角联锁结构中经纬纱排列的数字表达及其规律[J]. 纺织学报, 2015, 36(10)：29-32. XU He, TANG Yuyuan, MA Fei, et al. Digital expression and regularity of warp and weft repeat in angle-interlock structure[J]. Journal of Textile Research, 2015, 36(10): 29-32.

[9] CHEN X, SPOLA M, PAYA J G, et al. Experimental studies on the structure and mechanical properties of multi-layer and angle-interlock woven structures[J]. Journal of the Textile Institute, 1999, 90(1): 91-99.

[10] TAN P, TONG L Y, STEVEN G P. Micromechanics models for mechanical and thermomechanical properties of 3-D through-the-thickness angle interlock woven composites[J]. Composites: Part A, 1999, 30(5): 637-648.

[11] LAPEYRONNIE P, GROGNEC P L, BINÉTRUY C, et al. Homogenization of the elastic behavior of a layer-to-layer angle-interlock composite[J]. Composite Structures, 2011, 93(11): 2795-2807.

[12] CUI F, SUN B, GU B. Fiber inclination model for finite element analysis of three-dimensional angle interlock woven composite under ballistic penetration[J]. Journal of Composite Materials, 2010, 45(14): 1499-1509.

[13] LI Z, SUN B, GU B. FEM simulation of 3-D angle-interlock woven composite under ballistic impact from unit cell approach[J]. Computational Materials Science, 2010, 49(1): 171-183.

[14] TANG Y Y, SUN B Z, GU B H. Impact damage of 3D cellular woven composite from unit-cell level analy-sis[J]. International Journal of Damage Mechanics, 2010, 20(3): 323-346.

[15] SMITH J C, FRANK L. Stress-strain relationships in yarns subjected to rapid impact loading: partⅤ: wave propagation in long textile yarns impacted trans-versely[J]. Textile Research Journal, 1958, 28: 288-302.

[16] LUAN K, SUN B, GU B.Ballistic impact damages of 3-D angle-interlock woven composites based on high strain rate constitutive equation of fiber tows[J].International Journal of Impact Engineering,2013,57:145-158.

Modeling analysis on impact damage of 3-D angle-interlock woven composite based on finite element

MA Qian1, WANG Ke1, JIN Limin2，3,4

(1.CollegeofTextileandClothing,YanchengVocationalInstituteofIndustryTechnology,Yancheng,Jiangsu224005,China; 2.ShanghaiInstituteofAppliedPhysic,ChineseAcademyofSciences,Shanghai201204,China; 3.CollegeofTextiles,DonghuaUniversity,Shanghai201620,China; 4.HubeiKeyLaboratoryofAdvancedTextileMaterials&Application,WuhanTextileUniversity,Wuhan,Hubei430200,China)

In order to study high-velocity impact resistance of a 3-D angle-interlock woven composite (3DAWC) and guide the structural design of impact resistance materials, the dynamic mechanical responses of such composite subjected to the ballistic impact at serious striking velocities (500 m/s, 600 m/s and 800 m/s) were calculated by finite element analysis. By comparatively analyzing the velocity-time curves and acceleration-time curves of the projectiles with different striking velocities, as well as the progressive damage evolution and ultimate damage morphologies of composite targets, it is found that the velocity degradation process of the project can be divided into 2 stages. The fluctuation in acceleration can directly indicate the dynamic absorption law of 3DAWC target on kinetic energy of projectile. In addition, the bent regions in warp yarns are key structural parts for 3DAWC. Such local regions, therefore, should be strengthened and performed structural optimization for the design of impact-resistance type of 3DAWC.

three-dimensional angle interlock; composite; high-velocity impact; finite element analysis

10.13475/j.fzxb.20160805206

2016-08-24

2017-01-25

江苏省高校优秀中青年教师境外研修计划项目(苏教师(2014)24号)；江苏高校品牌专业建设工程一期项目(PPZY2015C254)；江苏高校优秀科技创新团队计划资助项目(苏教科(2015)4号)；生态纺织教育部重点实验室(江南大学)开放课题(KLET1505)；湖北省纺织新材料及其应用重点实验室(武汉纺织大学)开放课题(Fzxcl2017001)

马倩(1987—)，女，讲师，硕士。主要研究方向为纺织复合材料。金利民，通信作者，E-mail: lmjin@sinap.ac.cn。

TS 101.2

A