原液着色涤纶交织混色织物的颜色预测模型

李启正，朱炜婧，金肖克，祝成炎

(1. 浙江理工大学 材料与纺织学院、丝绸学院，浙江 杭州 310018；2. 浙江理工大学 杂志社，浙江 杭州 310018；3. 浙江科技学院 艺术设计学院，浙江 杭州 310023)



原液着色涤纶交织混色织物的颜色预测模型

李启正1,2，朱炜婧1,3，金肖克1，祝成炎1

(1. 浙江理工大学 材料与纺织学院、丝绸学院，浙江 杭州 310018；2. 浙江理工大学 杂志社，浙江 杭州 310018；3. 浙江科技学院 艺术设计学院，浙江 杭州 310023)

为准确预测色纱交织后形成的空间混合颜色，对以往圆柱形纱线的织物几何结构模型进行了改进，并提出了织物几何结构模型中纱线压扁系数的计算方法；在现有有色纤维混合和色纱交织混合颜色预测模型的基础上，构建了一个带经验系数和中间函数的新模型用于原液着色涤纶交织混色织物的颜色预测，并提出采用牛顿迭代确定经验系数的方法。为检验模型的准确性和有效性，设计并织造了单组纬显色和双组纬显色，4种经纬密度组合以及32种组织结构共288块原液着色涤纶长丝交织混色织物。研究结果表明：与以往固定形式的颜色预测模型相比，新模型的预测精度良好；在不同场合下，新模型可调整经验系数，以适用于不同类型色纱交织混合颜色的更准确预测。

机织物；原液着色涤纶；交织混色；空间混色；颜色预测；颜色模型；织物几何结构

将数种基本色的有色纱线进行交织，可获得丰富的织物空间混合颜色，如能实现颜色的准确预测和色差的有效控制，交织混色技术可替代大部分织物的印染工序。原液着色纺丝属于纤维本体着色，整个过程不产生印染废水，能耗低。采用原液着色纤维生产有色面料并替代传统织物的水印染工艺，这是清洁纺织的重要发展方向。原液着色涤纶织物色牢度好、挺括耐用，在军队服装、职业服、户外纺织品、窗帘等领域的应用日益广泛。原液着色纤维织物空间混合颜色的数字化表征、预测和计算机配色是交织混色技术推广和应用的关键[1]。色纱交织后的空间混合颜色可通过小样法、圆盘混色法、图像平均计算和比例法等进行预测。但圆盘混色和图像平均计算法预测精度较低，小样法费时费工；比例法根据织物表面各色纱的比例、线密度和颜色，以及织物经纬密度等的数学运算进行颜色预测，是一种快速且可通过计算机执行的颜色预测方法[2]。典型的研究有：Dimitrovski等[3]基于CIEL*a*b*色空间计算的交织颜色预测模型(简称LAB模型)；Kiyosawa等[4]基于色深K/S值(简称K/S模型)和反射率R(简称R模型)[5]计算的交织颜色预测模型；Mathur等[6]基于log(K/S)计算的交织颜色预测模型(简称LOG(K/S)模型)；陈子晗等[7]基于三刺激值(XYZ)计算的交织颜色预测模型(简称XYZ模型)；Chae等[8]基于反射率指数加权的Warburton-Oliver颜色预测模型(简称W-O模型)。

以上相关研究以其特定的交织混色织物为例，基于不同的颜色特征值进行交织混合颜色的计算和预测。但上述研究所用的织物几何结构都是理想的圆柱体纱线交织结构，颜色预测模型的形式也是固定的。文献[8-9]对已报道的机织物颜色预测模型进行了初步的优化和比较认为，大部分模型在预测精度和适用性方面还有不少局限。本文以具有广阔应用前景的原液着色涤纶长丝交织织物为例，研究适合其使用的、具有较好预测精度的，并具有一定适用性的颜色预测方法及计算模型。

1 织物几何结构模型的设计

1.1 模型的假设

为便于计算，以往交织混色织物颜色预测所用的几何结构模型中，通常假设纱线为理想的圆柱形，在交织过程中，纱线不发生压扁和扭曲变形。早在1937年，Peirce就提出了织物的几何结构模型设计理论，认为织物中经纬纱线的截面为圆形，但在经纬纱相互交织的地方会有弧形形变，其余为直线线段，织物中经纬纱交织处的屈曲波高等于经纬纱理论直径之和乘以压扁系数[10]。为考虑纱线在交织后的压扁情况，Kemp和Hearle等分别提出了跑道形[11]和透镜形[12]纱线截面理论。为简化模型且使模型具有一定的适应性，纱线形态的一致性仍是重要的假设；但需引入纱线压扁系数对纱线理论直径进行修正，因此，本织物几何结构模型的建立基于以下假设：

1) 织物中的纱线在交织后不发生弯曲和滑移等形态变化；

2) 织物中纱线各部分的颜色均匀一致，不受光照和交织屈曲的影响；

3) 织物中纱线的直径为理论直径乘以压扁系数，经纬纱线的压扁系数一致。

1.2 色纱比例的计算

以纬面5枚缎纹组织为例，推导织物表面经纬色纱比例(覆盖率)的计算公式。理想的二维织物几何结构如图1所示。

图1 纬面5枚缎纹织物几何结构示意图Fig.1 Schematic diagram of filling faced satin weave with unit of 5×5 repeat

图1中：dj为经纱直径；dw为纬纱直径；pj为织物中相邻经纱的间距；pw为织物中相邻纬纱的间距；Aj、Aw和Ao分别为经纱、纬纱和间隙在织物表面所占的比例，%；nj为1个组织循环内的经组织点数，示例中为5；nw为1个组织循环内的纬组织点数，示例中为20；n为组织循环数，示例中为5，如经纬组织循环相等，则存在关系n2=nj+nw。

因此，织物表面的经纬色纱及间隙比例可通过式(1)～(3)进行计算。

(1)

(2)

(3)

式中:ρj和ρw分别为织物成品的经、纬密度，根/cm；d为纱线直径，cm。其中ρ=1/p，Aj+Aw+Ao=1。

根据上述理想的织物几何结构，织物表面经纬纱线和间隙所占的理论色纱比例可通过纱线的真实直径、织物成品的经纬密度和织物组织进行计算。

1.3 纱线压扁系数的计算

本文研究中的原液着色涤纶长丝没有捻度，在交织和不交织的情况都会发生压扁形变，因此，不宜直接使用理想色纱比例进行交织混合颜色的预测。纱线压扁系数引入的主要目的在于修正理论色纱比例，因此，研究关键点在于找到可用于参照的织物表面真实色纱比例。

织物表面的真实色纱比例受纱线压扁、扭曲、滑移和遮盖等复杂因素的影响，本文提出基于图像处理技术的色纱真实比例统计方法。以实际织造的双纬显色织物色卡Ⅰ为例。首先采用高精度扫描仪(扫描分辨率为1 200像素)将织物色块与印刷胶片尺(精度为0.01 cm)一起进行扫描，再将扫描图放大到足够程度，采用图像处理软件框选单位面积内各色纱所占的图像像素，形成专色图，再采用直方图统计各专色在单位面积内所占的像素，计算各色纱所占的面积比例(图2)。本例中，双组纬显色织物共需要对16种组合的织物表面真实色纱比例进行统计。实际操作中发现，只要扫描稿精度足够，严格按照图像边缘进行颜色框选，不同操作人员统计得到的色纱比例误差在3%以内，证实本文方法用于统计真实色纱比例是准确可行的。

图2 色纱真实比例的统计方法Fig.2 Statistical method of yarn coverage actual percentage. (a) Diagram of pixel unit selected; (b) Histogram statistics results

将纱线压扁系数θ引入纱线直径的计算公式中，如式(4)所示。

(4)

式中：d为纱线直径，cm；Nt为纱线线密度，tex；δ为纱线的体积密度，g/cm3。

假设A为理论色纱比例，A′为图像统计得到的真实色纱比例，△A为理论色纱比例和真实色纱比例之间的偏差，则

(5)

式中：下标j、w、o分别代表经纱、纬纱和间隙；下标1和2代表甲纬和乙纬。

以织物色卡Ⅱ为例，采用迭代计算可得到压扁系数θ取值为1.21时，△A有最小值0.056。经过压扁系数的修正，理论色纱比例与真实色纱比例之间的偏差从修正前的14.1%降低到了5.6%。研究结果表明，压扁系数的引入大大提高了理论色纱比例的准确性，此压扁系数可应用于其他规格交织混色织物的色纱比例修正中。

2 实验部分

2.1 织物色卡的设计与制作

为使本文研究构建的颜色预测模型对于原液着色涤纶长丝织物具有较好的适用性，以常规原液着色涤纶FDY全拉伸丝为原料，设计了2种类型4种经纬密度组合共288块织物色样，并在喷水提花织机上进行织造，工艺参数见表1。

表1 交织混色织物色样的规格Tab.1 Specifications of interwoven color mixing fabrics

注：R、G、B、C、M、Y分别代表颜色红、绿、兰、青、品红、黄。

2.2 颜色的测试条件和计算

采用Datacolor SF600分光测色计测定色纱和交织混色织物的反射率。分光光度计测色孔径选用SAV(9 mm)，不包含镜面光泽，波长范围为400 ～700 nm，间隔为10 nm，仪器校准后误差△ECMC为0.14。色纱颜色采用玻片缠绕法进行反射率测定，交织混色织物采用正面单层进行反射率测定。

色纱色样和织物色样通过分光光度计测得反射率R(λ)后，根据CIE标准照明体D65的光谱能量分布和CIE1964 10°标准色度观察者的光谱三刺激值，求得D65光源、10°视场下纱线和织物对应的CIE1976L*a*b*颜色值。

3 颜色预测模型的构建

3.1 预测模型的推导

正常光照条件下，织物表面不同颜色的色纱会对入射光进行吸收、反射和散射，间隙则会对光线进行透射和吸收，由于色纱和色点非常细小，在一定距离外，人眼不能单独分辨这些细小的颜色，便产生了颜色的混合感觉。基于二光通理论和混沌介质的Kubelka-Munk理论给出色样反射率R与其吸收系数K和散色系数S之间的函数关系，可用于交织混色织物颜色预测计算时反射率R和色深K/S值之间的转换。研究发现，CIEL*a*b*值、反射率R、色深K/S值和三刺激值XYZ等色组分的加权和模型用于原液着色涤纶长丝交织织物的颜色预测时，预测精度和适用性并不好；基于大量的交织混色织物颜色预测实践，在总结前人对纤维混合和色纱混合颜色预测研究的基础上，本文提出如下模型建立思路。

文献[13]指出利用对数函数降低极值点和端点的思路将色纱K/S值求对数，建立了基于log(K/S)加权和的颜色预测模型，提高了模型的预测精度，表明中间函数有助于修正某些异常值，提高模型整体的预测精度；根据Stearns-Noechel[14]、Friele[15]等对有色纤维混色的预测经验和前期的研究[16]，经验系数有助于调整模型，以适合不同类型的纤维混色，提高模型的适用性。基于以上分析，设想建立关于色深K/S值的中间函数f[(K/S)λ]，从而使式(6)成立。

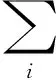
(6)

中间函数的定义如式(7)所示，其中σ为经验修正系数，其值根据实验和预测结果确定，对于不同规格纱线和品种的色样，σ有不同的最佳取值。

(7)

根据式(8)中Kubelka-Munk关于反射率R和K/S值之间的函数关系，式(7)可换算为式(9)用于计算机程序计算。

(8)

(9)

根据色组分i的光谱反射率和式(9)，可求得各色纱和组分的f[(K/S)i,λ]；根据色纱比例和式(6)，可求得各波长下织物的f[(K/S)mix,λ]；根据式(7)的逆运算式(10)和式(8)的逆运算式(11)，即可求得相应波长下交织混色织物的反射率Rλ。

(10)

(11)

3.2 经验系数σ的计算

为适应不同类型和不同规格试样的颜色预测，在颜色预测模型中引入经验系数σ，可对模型的预测进行适当修正。根据定义，K/S值不能为负数，因此，σ的有效取值范围为0～1。

为寻找合适的σ值，使2.1中制作的所有交织混色织物颜色预测的平均色差最小，将288块交织混色试样放在同一个模型中进行多次迭代计算，得到全部交织混色织物颜色预测CMC(2∶1)平均色差与σ取值之间的关系，如图3所示。由图可看出σ值与预测平均色差呈现一个明显的U形分布关系，因此，必然存在一个最佳σ值，使得整体预测色差最小，预测精度最高。从图中可发现，σ=0.275时，288个色样的平均CMC(2∶1)预测色差达到最小，为3.175。同时，从图中还可看出，σ在底部的一定范围内，整体预测平均色差的变化比较小。

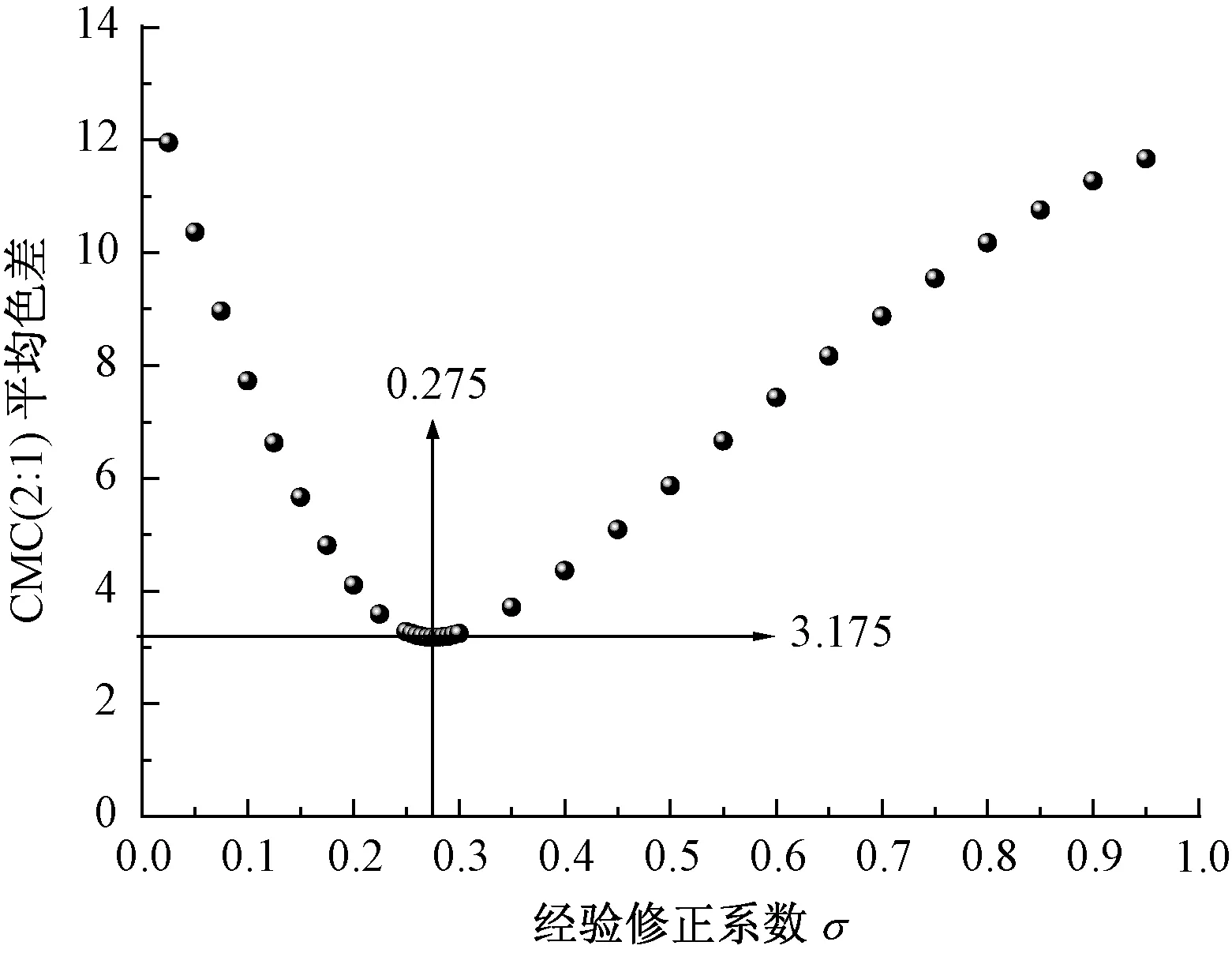
图3 经验系数与全部色样颜色预测平均色差之间的关系Fig.3 Relationship between experience coefficient and average predicted color-difference of all samples

4 模型的比较与评价

已报道的交织混合颜色预测模型研究中，部分研究基于理想圆柱形纱线结构模型给出了色纱比例的计算方法；部分研究直接采用了真实的色纱比例用于颜色计算，取得了较好的预测结果。需要指出的是，准确和可运算的色纱比例计算方法是计算机颜色预测和配方计算的前提和基础。

整体看来，直接采用实际色纱比例进行计算的模型一般都得到了较好的预测结果，此外，精细织物的颜色预测也比粗糙织物的预测精确，因此，色纱比例的准确性也是颜色模型预测精确与否的关键因素。为平行比较各模型用于原液着色涤纶长丝交织织物颜色预测时的适用性和准确性，以下模型所用的色纱比例均采用本文提出的修正织物几何结构模型进行计算。

4.1 新模型的预测结果

根据1.2的理论色纱比例计算方法和3.1建立的颜色预测模型，纱线压扁系数θ取值为1.21，经验修正系数σ=0.28时，采用新模型对4种规格色卡的288个织物色样进行颜色预测。为便于比较，符合行业习惯并适应色度学发展，对预测颜色值与实际光谱颜色值之间的CIELAB、CMC(2∶1)和CIEDE 2000(2∶1∶1)3种色差进行统计，结果如图4所示。将其中288个CMC(2∶1)色差按照组织编号次序进行柱状图统计，结果如图5所示。

图4 新模型用于全部交织色样颜色预测的色差箱线图Fig.4 Color-difference box-plots of all samples predicted by new model

图5 全部交织色样颜色预测的CMC(2∶1)色差分布Fig.5 Color prediction result and CMC(2∶1) color-difference distribution of all interwoven fabric samples

图4的色差箱体统计表明，新模型对单组纬或双组纬显色、不同经纬密度组合及不同组织结构的原液着色涤纶长丝交织织物均具有良好的预测性能，288个色样的平均CMC(2∶1)色差已降至3.18，且在288个色样中，有83%的色样其CMC(2∶1)色差小于或等于5，因此对于采用理论色纱比例来计算的预测模型来说，新模型具有良好的预测精度，并可保持稳定的预测性能。

图5中从左至右的色样序号为织物色样的名称排序，即Ⅱ(A)→Ⅱ(B)→Ⅱ(C)→Ⅰ。Ⅱ系列色样有几个较为明显的大色差集中区，经分析发现，这些大色差主要为绿色纬线与米色经线的交织色样。统计还发现，192个Ⅱ系列色样中，CMC(2∶1)预测色差大于4的有57个色样，其中只有8个不是绿色系色样。经多次实验测试比较，绿色纱线的反射率测试结果是正确且可靠的。对于出现上述现象的原因，本文有如下2点解释。

1) 模型的经验系数是根据色差计算结果进行迭代计算得到的，根据文献[17]开展的对色差公式颜色辨别特性的研究，所有色差公式，包括CMC色差公式在绿色(green)和蓝绿色(blue-green)区域的预测性能是最差的，因此，这部分织物的色差比较大。

2) 根据CIE对光响应平均值的研究，人眼对明视曲线(photopic vision)范围内的绿光辨别能力最强。图6示出明视曲线和青色、绿色纱线的反射率，450～500 nm区域为蓝光范围，500～570 nm为绿光范围。本文研究选用的绿色纱线反射率大部分落在明视范围内，而选用的青色纱线只有一小部分落在明视范围内，故新模型得到的颜色预测结果中，绿色系交织混色织物的预测色差最大。新模型对于含绿色纱线织物的颜色预测较敏感，与明视曲线辨认特征相符。

图6 明视曲线和青色、绿色纱线的反射率Fig.6 Photopic vision curve and reflectance curves of cyan and green yarns

4.2 模型的平行比较

在印刷和染色工业中，一般要求色差控制在1以内，但根据以往对机织物颜色预测的研究，CIELAB色差控制在2～5之间便被认为已具有较好的预测精度[18]。将新模型和6个已报道的颜色预测模型共同用于288块交织织物色样的颜色预测，并将预测结果与分光光度计测试结果进行色差比较，结果如表2所示。

表2 不同模型用于全部色样颜色的预测Tab.2 Color prediction of all fabric samples by different models

7种模型的预测结果中，K/S模型预测效果最差，基本不能反映织物交织后的真实颜色；R和XYZ这2个预测模型预测结果接近，但二者的预测精度都不高；CIELAB和LOG(K/S)模型颜色预测性能良好，且预测精度与Mathur[6]在涤/棉交织混色预测中的结果接近；W-O模型和本文提出的新模型的预测性能最好，CMC(2∶1)平均色差已接近3，但预测效果最好的还是本文提出的新模型，CIELAB、CMC和CIEDE2000 3种色差的平均值都是最低的。

相比较固定形式的W-O模型，新模型的优势还在于对不同规格的试样类型，可选用不同的经验系数，以使得其在各种情况下都有更好的适用性。对2.1中制作的4种规格的试样进行单独迭代计算，可得到4种规格试样平均颜色预测色差最小时的经验系数，结果如表3所示。

表3 不同经验系数取值时各系列色样颜色预测结果Tab.3 Color prediction results of each set of fabrics with different empirical coefficients

注：N表示本文新模型。

当经验修正系数σ=0.28时，全部色样整体预测平均色差达到最小(CMC(2∶1)=3.18)。σ的取值区间在0.22～0.36时，分别得到不同规格系列色样的最佳预测结果。相比较固定形式的颜色预测模型，新模型通过微调经验系数可更好地适应不同规格的色样。本文研究中，只要σ的取值在建议的合理范围内，并不会造成其他系列色样预测精度的明显降低，因此，经验系数σ为0.28可用于本文研究各规格原液着色涤纶交织混色织物颜色的准确预测。

值得一提的是，本文研究中所用FDY纱线的压扁系数(θ=1.21)是基于Ⅰ系列色样求得的，然后将此压扁系数用于所有色样的色纱比例修正，再将所有288块织物色样用本文介绍的7个模型进行颜色预测，纱线压扁系数的引入明显降低了全部7个模型的预测色差，模型的预测精度平均提高1个CMC(2∶1)色差单位。

5 结 论

1) 以往圆柱形纱线的织物几何结构模型在计算低捻度纱线和非紧密交织织物的理论色纱比例时存在较大的误差，引入纱线压扁系数有助于修正理论色纱比例。实际中可采用扫描加直方图法统计织物表面的真实色纱比例，操作方法直观，设备要求低，精度高，适用于不同原料和规格织物纱线压扁系数的推算。

2) 交织混色织物的混合颜色为织物表面各色纱组分及间隙的颜色贡献之和。反射率、三刺激值和CIEL*a*b*等都可用于各颜色组分的贡献值计算，但这些模型的预测精度不足。

3) 中间函数和经验系数有助于提高模型的预测精度和适用性。较以往固定形式的颜色预测模型，新模型在预测精度方面取得了明显的进步。另外，新模型的优势在于在不同场合下可调整经验系数，以适用于不同规格色样的更精确预测。

FZXB

[1] 金剑, 李鑫, 王颖,等. 原液着色纤维产业“十三五”发展路径[J]. 中国纺织, 2016(12):64-65. JIN Jian, LI Xin, WANG Ying, et al. Development path of dope-dyed fiber industry in 13th Five Year Plan[J]. China Textiles, 2016(12):64-65.

[2] 章斐燕, 金亦佳, 李启正, 等. 空间并置混色色织物颜色预测方法的比较研究[J]. 丝绸, 2014, 51(11): 22-27. ZHANG Feiyan, JIN Yijia, LI Qizheng, et al. Comparative study of color prediction methods of yarn-dyed fabrics with spatial juxtaposition[J].Journal of Silk, 2014, 51(11): 22-27.

[4] KIYOSAWA T, ZHENG J, KOMATSU T, et al. Color prediction of union fabric considering mutual reflection between yarns[J]. SEN-I Gakkaishi, 2006, 62(9): 212-217.

[5] KIYOSAWA T, ZHENG J, TAKATERA M, et al. Color prediction of union fabrics considering mutual reflection between yarns: a new color prediction model using apposed color mixture theory[J]. SEN-I Gakkaishi, 2007, 63(5): 117-122.

[6] MATHUR K, HINKS D, SEYAM A F M, et al. Towards automation of color/weave selection in jacquard design: model verification[J]. Color Research & Application, 2009, 34(3): 225-232.

[7] 陈子晗. 织物结构设计与织物色彩关系的研究与应用[D]. 上海：东华大学, 2015：46-66. CHEN Zihan. Research and application of the relationship between fabaric structure and fabric color[D]. Shanghai: Donghua University, 2015：46-66.

[8] CHAE Y, XIN J H, HUA T. Color prediction models for digital Jacquard woven fabrics[J]. Color Research & Application, 2016, 41(1): 64-71.

[9] ZHANG S S, LIU X Y, YU W D. Evaluation and model of woven fabric color[J]. Advanced Materials Research, 2013, 627: 195-199.

[10] 蔡雨, 郑天勇, 景书娟, 等. Peirce 平纹机织物结构模型的计算精确度[J]. 纺织学报, 2012, 33(1): 48-53. CAI Yu, ZHENG Tianyong, JING Shujuan, et al. Verification of the Peirce′s model for the geometric structure of the plain woven fabrics[J]. Journal of Textile Research, 2012, 33(1): 48-53.

[11] 彭淑静. 圆环形织物的织造研究[D]. 天津: 天津工业大学, 2006: 4. PENG Shujing. Research on weaving of annular shaped fabrics[D]. Tianjin: Tianjin Polytechnic University, 2006: 4.

[12] HEARLE J W S, GROSBERG P, BACKER S. Structural mechanics of fibers[J]. Yarns and Fabrics,1969, 28(1): 85-87.

[13] SEYAM A F M, MATHUR K. A general geometrical model for predicting color mixing of woven fabrics from colored warp and filling yarns[J]. Fibers and Polymers, 2012, 13(6): 795-801.

[14] STEARNS E I, NOECHEL F. Spectrophotometric prediction of color of wool blends[J]. American Dyestuff Reporter, 1944, 33(9): 177-180.

[15] FRIELE L F C. The application of color measurement in relation to fibre-blending[J]. Journal of the Textile Institute, 1952, 43: 604-611.

[16] LI Q Z, ZHANG F Y, JIN X K, et al. Optimized stearns-Noechel model to predict mixed color values of yarn-dyed fabrics[J]. Fiber, 2014, 70(9):218-224.

[17] 汪哲弘. 颜色视觉辨别特性及色差评价研究[D]. 杭州: 浙江大学, 2009: 57. WANG Zhehong. Study of color vision discrimination characteristics and color-difference evaluation[D]. Hangzhou: Zhejiang University, 2009: 57.

Model for predicting color mixing of dope-dyed polyester interwoven fabrics

LI Qizheng1,2, ZHU Weijing1,3, JIN Xiaoke1, ZHU Chengyan1

(1.SilkInstitute,CollegeofMaterialsandTextiles,ZhejiangSci-TechUniversity,Hangzhou，Zhejiang310018,China; 2.PeriodicalsAgency,ZhejiangSci-TechUniversity,Hangzhou,Zhejiang310018,China; 3.SchoolofDesign,ZhejiangUniversityofScience&Technology,Hangzhou，Zhejiang310023,China)

In order to more accurately predict the spatial mixed color of dope-dyed polyester interwoven fabrics, the classical cylindrical section fabric geometric structure model was improved, and the computing method of yarn flattening coefficient after interwoven was proposed. Then, a new color prediction model with intermediate function and empirical coefficient was built based on the analyses of existing fiber blended and yarn interwoven color prediction models, which is suitable for the dope-dyed polyester interwoven color mixing fabrics. Meanwhile, the iteration method for determining the optimal empirical coefficient was introduced. Finally, total 288 pieces of dope dyed polyester interwoven fabrics including 2 types of fabric specifications, 4 combinations of warp/weft density, and 32 weave structures, were woven for validation and evaluation on the accuracy and effectiveness of the new model. The results show that the prediction accuracy and applicability of new model are superior to those of the existing fixed form color prediction models. The advantage of new model is that its empirical coefficient can be adjusted for different types of interwoven fabrics so as to obtain a more accurate color prediction.

woven fabric; dope-dyed polyester; interwoven color mixing; spatial color mixing; color prediction; color model; fabric geometric structure

10.13475/j.fzxb.20160506708

2016-05-25

2017-04-14

国家国际科技合作专项项目(2011DFB51570)；浙江理工大学科研启动基金资助项目(15012164-Y)

李启正(1981—)，男，讲师，博士。主要研究方向为纺织颜色科学与技术。E-mail：liqizheng@zstu.edu.cn。

TS 156；TS 105.1

A