机床床身的动力学模型修正技术研究
葛泽稷,丁晓红,张 横
(上海理工大学 机械工程学院,上海 200093)
机床床身的动力学模型修正技术研究
葛泽稷,丁晓红,张 横
(上海理工大学 机械工程学院,上海 200093)
针对有限元建模中边界条件难以确定的问题,文中以某型床身为研究对象,以模型修正为目的,通过参数型模型修正方法,对模拟床身与地基之间边界条件的弹簧单元垂直方向的刚度进行参数化优化,以修正床身的有限元模型。通过这种修正技术实现了对床身有限元模型的修正,优化后床身频率以及振型与试验分析所得结果基本一致。结果表明,该方法可以有效地完成模型修正工作,修正结果也较为精确。
机床床身;模型修正;弹簧单元
在概念设计和图纸设计阶段,通过有限元仿真模型的预测,就能进行初步的产品结构动态特性的评价与优化改进。在另外一些情况下,如在无法或是很难进行实验时,有限元仿真是用于评价和决策的唯一手段。因此,提高有限元模型计算精度对实际的工程问题显得尤为重要[1]。
在当代的机床结构优化设计中,计算机辅助分析(Computer Aiding Engineering,CAE)的优势日益显现。不仅利用有限元模型的分析结果可使机床设计周期大幅缩短,而且可在设计初期利用有限元分析模型的结果取代传统的大量实际试验,从而降低设计成本。固然,有限元模型在处理复杂结构上具有明显的优势,但仅凭工程师的经验,欲建立一个与试验结果相一致的有限元模型有较大的困难。尤其当需分析的结构比较复杂时,且没有一个正确的数学模型,较难对后续响应分析做出准确的预测[2-4]。目前对于有限元模型中的建模误差可以归纳为3类[5]:(1)模型结构误差(Model Structure Errors)。结构的有限元模型不能真实地反映结构原有的特性;(2)模型参数误差(Model Parameter Errors)。主要指有限元模型的设计参数误差,这类误差主要由建模过程中设计参数的不确定性引起,是有限元模型修正研究主要的修正对象;(3)模型的离散化误差。有限元模型的自由度数偏低,通常出现于复杂结构离散化的情况,该类误差也可以视为结构误差的一种。
本文针对在机床床身的有限元模型与试验模型之间存在较大差异的问题,提出以结合有限元分析技术与试验模态分析技术的方法。利用试验获得的模态分析的结果来修正有限元模型,从而获得高精度的有限元模型。修正后的有限元模型可以作为后期相关分析的基础模型,如结构响应预测、动力修改、优化设计、可靠性分析、破损监测与故障诊断等工程应用服务。
1 有限元模型的修正
固有频率通常是动力学分析中最基本的参数,而且比模态向量更容易测量(仅限于低阶固有频率,高阶固有频率比低阶固有频率更容易受有限元模型离散程度的影响)[6]。试验测量频率Ft与有限元计算频率ft之间的相关程度通常表示为
C%=(Ft-ft)/ft
(1)
本文主要以H234磨床床身为研究对象,首先通过试验分析获得机床床身的前6阶固有频率及其振型;然后再建立其的有限元模型。由于难以精确模拟机床下的垫铁单元,因此考虑用弹簧阻尼单元来模拟垫铁单元。通过参数型模型修正的方法,以试验测量的频率与有限元分析得到的频率差值最小为目标函数,以弹簧刚度为设计变量,再对比相同频率下的振型是否一致。如果不一致,则继续修改。如果一致,则提取这些接触刚度的具体数值,来建立较为精确的有限元模型。
2 床身的试验模态分析
本文采用锤击法来测试机床床身的固有频率。试验的设备选用:加速度计选用奇石乐(Kistler)公司8395A2D0ATTA00型号三轴加速度传感器,测量范围±2 g,灵敏度2 000 mV/g;力锤选用奇石乐(Kistler)公司9728A20000型号力锤,锤击力范围0~20 000 N,灵敏度0.2 mV/N;数据采集卡选用NI公司的NI9234模拟输入模块;数据采集分析软件为ModalVIEW。图1为有限元模型中机床床身的前6阶固有频率及其对应的振型,表1为实际试验测试机床床身的前6阶固有频率。

图1 有限元模型中的床身的振型图

前3阶固有频率频率值/Hz振型描述第1阶101.3整体上下振动第2阶119.8床身的前后摆动续表1第3阶141.8床身的左右摆动第4阶236.1床身整体扭动第5阶255.0右端(头架一端)部分的前后晃动第6阶272.1左端(尾架一端)部分的前后晃动
3 有限元模型的建立及模型修正
图2所示为由床身-垫铁-地基组成的弹性系统,床身是通过垫铁与地基接触。有限元模型中通常直接在垫铁位置处建立约束,但这样会导致约束刚度与实际情况相比不符。上述建模方法误差主要来源于机床床身与地基之间接触刚度的模拟误差,这种误差使得机床床身的有限元模态分析结果不精确;而在本文则把该刚度作为弹簧阻尼单元来处理,如图3所示可见垫铁主要是垂直方向支撑,因此弹簧只需要设置垂直方向刚度,其他两个方向刚度较小可不设置。为了减少计算规模,对床身结构的有限元模型进行简化[7-8],把一些对有限元模型分析影响小的几何特征,如细小的螺栓孔以及细小的倒角结构进行简化处理,从而提高该部分的网格质量。

图2 床身垫铁图
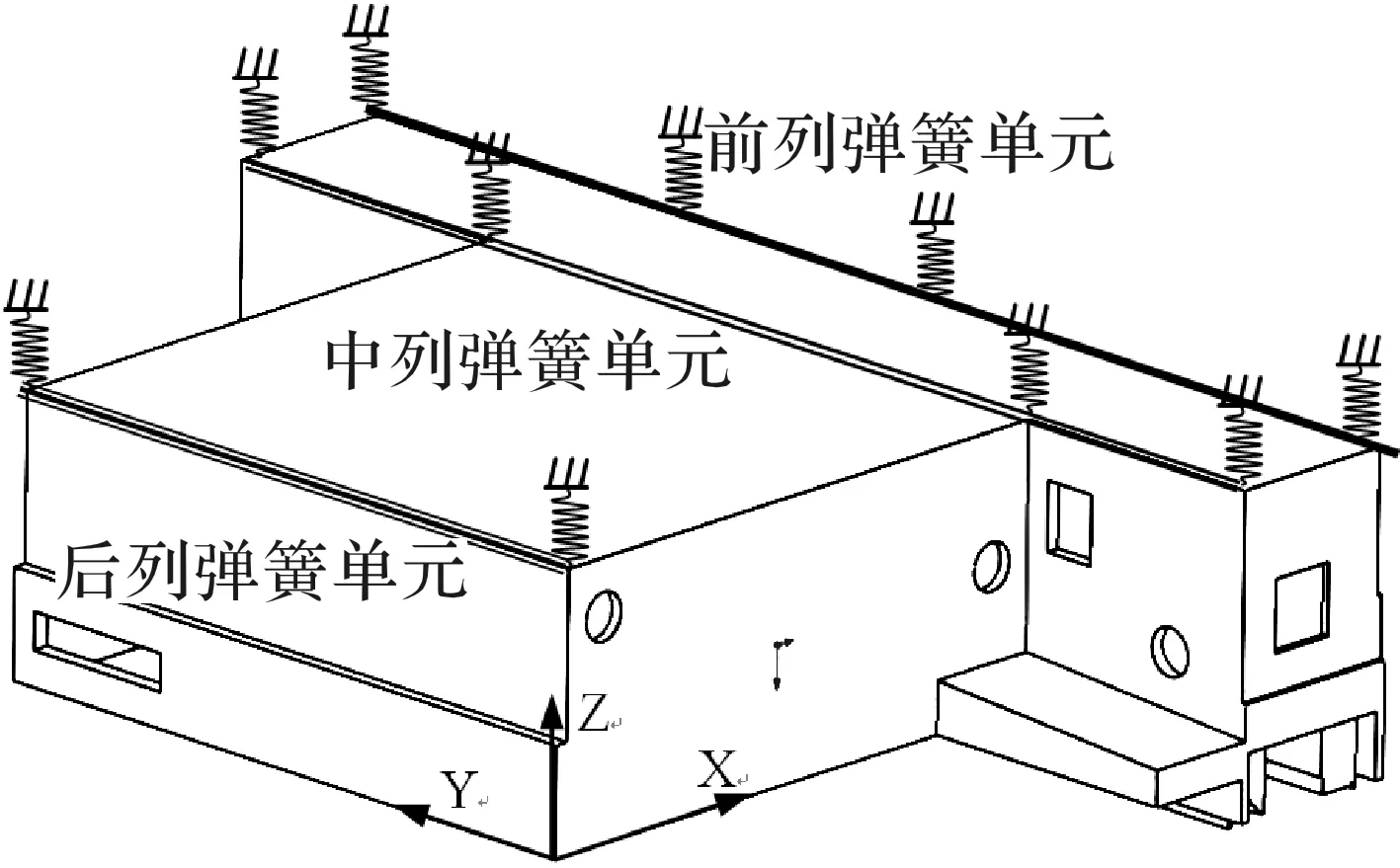
图3 模型修正的床身结构有限元模型
根据模型修正的对象不同,结构动力学模型修正可分为矩阵型修正方法和设计参数型修正方法。由于矩阵型修正方法修正后质量矩阵及刚度矩阵不再满足带状稀疏矩阵及对称性要求,从而使得修正结果失去物理意义,无法应用于工程实际,逐渐被参数型修正方法取代[9-11]。参数型修正方法本质上可归结为单目标参数的多变量优化问题,使用这种基于优化分析的模型修正法可以避免工作的盲目性,提高工作效率[12-13]。在机床床身的有限元模型中可以构造以前六阶固有频率为参数,并以机床床身与地基之间弹簧单元的垂直方向刚度作为设计变量,最小二乘法为目标函数[14-15],从而得到修正后的数学模型,如式(2)所示

(2)
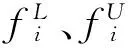
根据上述数学模型,通过迭代优化过程,寻找最终的设计空间参数向量,达到模型修正的目的。本文设计空间的设置以及优化后的弹簧刚度值如表2所示。

表2 设计变量参数表 /N·mm-1
4 优化后床身结构的模态对比
按优化后弹簧刚度参数对机床床身结构进行模态分析,可以得其到前6阶固有频率及其振型。表4所示的机床床身前6阶固有频率,图4为试验以及优化后床身的振型图。经分析可以看出,该床身的固有频率已于试验分析得到的频率一致且振型也一致,第1阶固有频率的误差为4.3%,第2阶固有频率的误差为0.2%,第3阶固有频率的误差为0.7%,第1阶固有频率的误差为0.6%,第1阶固有频率的误差为0.3%,第,1阶固有频率的误差为3.1%。可见优化前后的前6阶固有频率误差基本保持在5%的范围内。

图4 优化后各阶固有频率下的振型对比

阶数试验频率/Hz有限元分析频率/Hz误差/%第1阶101.396.94.3第2阶119.8120.00.2第3阶141.8142.80.7第4阶236.1237.60.6第5阶255.0255.80.3第6阶272.1280.53.1
5 结束语
本文针对床身有限元模型约束刚度难以确定的问题,运用参数型修正方法对机床床身与地基之间的接触弹簧单元垂直方向的刚度问题进行参数化优化,来修正床身的有限元模型。经过优化后的床身模态分析结果与试验结果误差控制在5%以内。通过这种尺寸优化技术实现了对床身模型的动力学修正,为模型修正提供了一种较为简单实用的方法。
[1] 郭勤涛,张令弥,费庆国.结构动力学有限元模型修正的发展—模型确认[J].力学进展,2006,36(1):36-42.
[2] 张松波,周建文.基于LMS Virtual.Lab 的汽车模态相关性分析与优化[J].汽车技术,2010(7):16-19.
[3] 杨勇明.基于有限元的蜗轮蜗杆传动性能模态分析[J].电子科技,2016,29(8):28-30.
[4] 杨广泽,马晓明.串联机械臂运动控制系统设计[J]. 电子科技,2016,29(3):71-74.
[5] Mottershead J E,Friswell M I.Model updating in structural dynamics: a survey[J].Journal of sound and Vibration,1993,167(2):347-375.
[6] 朱安文,曲广吉,高耀南,等.结构动力模型修正技术的发展[J].力学进展,2002,32(3):337-348.
[7] 洪清泉,赵康,张攀,等.OptiStruct&HyperStudy理论基础与工程应用[M].北京:机械工业出版社,2013.
[8] 王钰栋,金磊,洪清泉,等.HyperMesh&HyperView应用技巧与高级实例[M].北京:机械工业出版社,2013.
[9] 李德葆,陆秋海.工程振动试验分析[M].北京:科学出版社,2004.
[10] 张阿舟.实用振动测量与实验[M].北京:航空工业出版社,1997.
[11] 刘东,廖日东,左正兴.分析/试验模型相关及修正技术若干问题[J].强度与环境,2003,30(1):23-30.
[12] 刘江.ANSYS 14.5 Workbench机械仿真实例详解[M].北京:机械工业出版社,2015.
[13] 张洪才.ANSYS 13.0从人门到实战[M].北京:机械工业出版社,2010.
[14] 高星亮,张进忠,王祖光.基于模态参数计算边界条件的方法[J].振动测试与诊断,2005,25(1):56-60.
[15] 杨智春,王乐,李斌,等.结构动力学有限元模型修正的目标函数及算法[J].应用力学学报,2009,26(2):288-296.
Research of the Correction Technique of Dynamic Model of Machine Tools
GE Zeji,DING Xiaohong,ZHANG Heng
(School of Mechanical Engineering,University of Shanghai for Science and Technology,Shanghai 200093,China)
Aiming at the uncertain problems of boundary conditions in finite element analysis, this paper takes a machine tool bed as the research object, for the purpose of model updating, using the parameter model correction method to optimize vertical stiffness of the spring ,which simulate the stiffness between machine tool bed and ground, the optimization method is parametric optimization method, by this correction technology get model updating of machine tool bed in structural dynamics, the frequency and vibration mode of optimized bed are same with test analysis. Result shows that the method can effectively complete model updating work, the correct results are accurate.
machine tool bed;model updating;spring element
2016- 10- 31
上海市教委科研创新重点项目(13ZZ114);上海市研究生创新基金项目(JWCXSL1302)
葛泽稷(1992-),男,硕士研究生。研究方向:机床动力学特征分析。丁晓红(1965-),女,博士,教授。研究方向:机械优化设计。
10.16180/j.cnki.issn1007-7820.2017.08.019
TH391.9
A
1007-7820(2017)08-070-03

