基于主成分分析法和遗传算法优化支持向量机模型的泥石流危险度预测

基于主成分分析法和遗传算法优化支持向量机模型的泥石流危险度预测

一、引言

我国幅员辽阔，地形多山，泥石流灾害频发，其短时间内造成的巨大破坏严重威胁山区人民的生命财产安全[1-3]，因此对泥石流进行危险度预测有着至关重要的现实意义。

泥石流危险度受多个影响因子共同作用，且危险度与指标之间的复杂关系很难直观地表示出来。针对这一难题，许多专家学者进行了深入的探索和研究。陈华[4]等引入BP神经网络对泥石流危险度进行评价，沈简[5]等利用模糊数学建立了泥石流危险度综合评判模型，毛硕[6]等将层次分析法和灰色关联度法相结合对泥石流危险度进行了预测。以上研究均取得了一定的效果，但神经网络存在收敛速度过慢、局部最小值的缺陷，模糊数学本身的隶属度函数制定规则缺少必要的依据。

基于此，本文提出了主成分分析法和遗传算法优化的支持向量机模型，实现对泥石流危险度的预测。首先采用主成分分析法提取泥石流危险度影响因子的主成分，然后利用遗传算法优化支持向量机参数，训练得到PCA-GA-SVM模型，用该模型对预测泥石流沟样本的危险度进行预测，为泥石流危险度评价提供了一个新的思路。

二、基本原理

（一）主成分分析法

主成分分析法[7-8]是通过构造原变量的线性组合来得到维数较少且互不相关的新变量，这些新变量能够反映原始变量所提供的大部分信息，通过分析新变量来解决实际问题。其具体实现步骤为：设（X1, X2,…,Xn）是总体X的n个样本，每个样本观察m维变量，观测数据矩阵可记为：

首先计算该矩阵的协方差阵，为了避免不同变量间量纲差异导致的总体方差受较大方差变量控制的问题，根据公式将协方差阵化为其对应的相关系数阵。然后求出相关系数阵的特征值λ1≥ λ2≥ … λm≥0，计算得到它们对应的正交单位化特征向量e1,e2,…,em。第i个主成分的贡献率为λi/P，其中i=1, 2, 3, …,m，前q个主成分的累计贡献率为当前q个主成分累计贡献率达85%以上时，用这q个主成分来代替初始的影响因素进行分析，一般是满足工程要求的。

（二）遗传算法

遗传算法[9-10]是一种汲取自然进化基本思想寻求最优解的方法，有较强的全局优化特性和全局搜索能力。其基本思路为：任取一组参数作为支持向量机初始参数，并对参数进行编码，编码原则视具体情况需要，从而构造了第一代遗传群体；通过计算误差求出其适应度。若误差越大，则适应度越小；将所有适应度大个体遗传给下一代；通过对当前一代群体算子进行交叉、变异等遗传操作处理，产生下一代群体；重复以上步骤，不断优化支持向量机参数，直到参数满足条件或达到最大迭代次数。

（三）支持向量机

支持向量机[11-14]是由Vapnik于1995年根据统计学习理论提出的一种在有限样本下进行机器学习的方法，其原理如下：

其中：w称为可调的权值向量，b为偏置值，且w和Φ(Xi)均为n维向量。寻找最优的分类超平面亦即寻找最优的w和b。由于拟合误差的存在，引入ξ和ξ*作为松弛变量，采用ε-SVR模型建立带有约束条件的模型优化函数：

将(3)式分别对w和b求偏导并置零，反代回(3)式中就可以得到上述问题的对偶问题，找到对应的KKT条件，并使用二次规划优化算法（Sequential Minimal Optimization，SMO）作为训练算法依次计算得到参数对应的最优乘子同时构造得到预测函数：

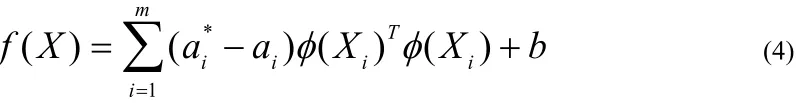
非线性映射Φ的表达式很难确定，故引入核函数（Kernel）将原始特征的内积平方和等价为映射后的特征内积平方和，从而间接的求解非线性映射Φ。满足泛函Mercer定理的核函数均可作为有效核函数，其中径向基核函数具有较宽的收敛域，为解决实际问题中最常用的核函数。

三、泥石流危险度预测

通过总结分析前人经验，采用云南省37条泥石流沟数据为样本（见表1），随机选择28条泥石流沟作为学习样本训练支持向量机模型，剩余9条泥石流沟作为预测样本。输出为泥石流危险度，分为4类：轻度危险、中度危险、高度危险和极度危险，对应数值分别为1、2、3、4。

其中，S1：一次泥石流（可能）最大冲出量（104m3）；S2：泥石流发生频率（次/100a）；S3：流域面积（km2）；S4：主沟长度（km）；S5：流域最大相对高差（km）；S6：流域切割密度（km/ km2）；S7：泥沙补给段长度比。

表1 云南省37条泥石流沟原始数据

（一）主成分分析

利用PCA对7个泥石流危险度影响因子进行分析，相关系数矩阵如表2所示，得到归一化特征值，各成分贡献率和累计贡献率如表3所示。从表3中可以看出，前4个主成分的累计贡献率为89.037%，基本能够反映原来7个变量所携带的信息。这3个主成分的表达式见式（5）。将提取出的3个线性无关的主成分代替原来的7个影响因素作为输入变量来建立支持向量机模型，模型维度由7维降低到3维，大大简化了模型的建立与运算。

表2 相关系数阵

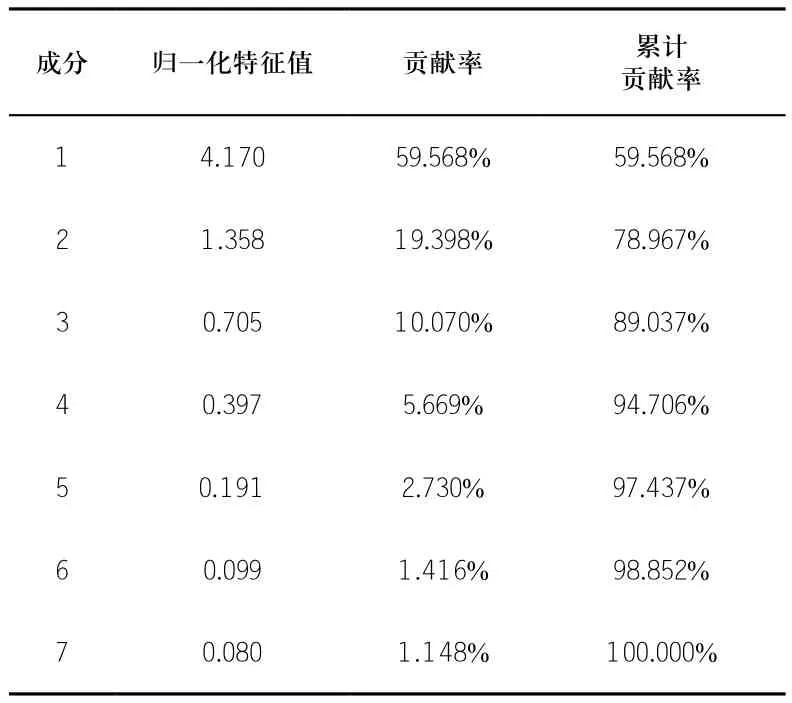
表3 归一化特征值、贡献率和累计贡献率

（二）模型建立

本文选取SVM的核函数为（RBF）径向基函数，同时运用MATLAB语言编写GA优化SVM模型参数程序，以式（5）的3个主成分作为输入变量，采用遗传算法确定SVM的参数C和g，种群数量n=20，终止代数为100，经过多次训练，得到最优的遗传算法适应度曲线如图1所示。确定SVM的最优惩罚参数为c=74.655，g=46.221。利用参数c和g确定的GA-SVM模型对学习样本进行训练和回判，结果如图2所示。

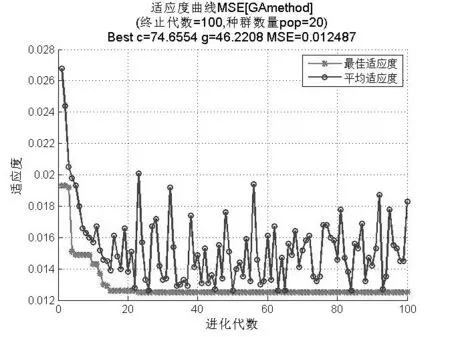
图1 遗传算法适应度曲线

由图2可以直观的看出，前28条泥石流中第2、16和27回判偏高，其余全部一致，回判准确率达89.3%，综合分析误差可知危险度为1类的泥石流仅有两条，数据信息较少影响对SVM模型的训练，回判出现误差，而且第27条黑水河泥石流发生频率较高，若发生泥石流易造成重大灾害，定为高危险等级（即3类）较为合理。因此该模型回判准确能够满足工程要求，可以用于预测样本的预测。

图2 学习样本回判结果

（三）预测结果与分析

将建立的PCA-GA-SVM模型用于预测样本的预测，同时运用未经主成分分析的学习样本原始数据训练GA-SVM模型，并对预测样本进行预测，两种模型预测结果如表4所示。

表4 两种模型预测结果

从表4中可以发现9条泥石流中仅小白泥沟预测偏高，其余全部一致，预测准确率达88.9%，而小白泥沟发生频率高，一次性冲出量大，定为4类危险度较为合理，表明运用PCA-GA-SVM模型预测泥石流危险度是有效的。此外，无论是将原始数据还是提取的主成分作为模型输入，支持向量机的泥石流危险度预测模型均有着很高的准确率，再次证明了支持向量机在解决小样本、非线性、高维数问题时具有独特的优越性。同时也可以看到，在运用主成分分析法降低样本维度缩短运行时间的情况下，模型的预测精度并未受到影响。

四、结论

1．泥石流危险度受多个影响因子间共同作用，主成分分析法降低了影响因子的维度，确定的3个主成分代表了7个变量所携带信息量的89.037%，有效地剔除了变量之间的冗余信息，提高了模型运行效率。

2．GA遗传算法具有易于实现、收敛速度快且能够找到全局最优解的特点，寻优得到了最优的支持向量机参数c=74.655，g=46.221，由此建立的PCAGA-SVM模型预测准确率达88.9%，预测精度满足工程要求。

3．泥石流危险度与多个影响因子间存在复杂的非线性关系，本文通过主成分分析法结合遗传算法优化的支持向量机模型较好地实现了泥石流危险度预测，但模型的普遍适用性还需要进一步验证。

[1] 陈鹏宇, 乔景顺, 彭祖武, 等. 基于等级相关的泥石流危险因子筛选与危险度评价[J]. 岩土力学, 2013(5): 1409-1415.

[2] 刘希林. 沟谷泥石流危险度计算公式的由来及其应用实例[J].防灾减灾工程学报, 2010(3)：241-245.

[3] 袁颖, 王晨晖, 周爱红. 泥石流危险性评价的支持向量机模型相关问题研究[C]//第十届全国工程地质学术年会论文集. 成都：科学出版社, 2016: 841-847.

[4] 陈华, 上官云龙. 基于BP神经网络的方法评价泥石流危险度[J].山西建筑, 2013(10): 89-90.

[5] 沈简, 饶军, 傅旭东. 基于模糊综合评价法的泥石流风险评价[J]. 灾害学, 2016(2): 171-175.

[6] 毛硕, 王运生, 曹水合. 基于可拓和组合赋权的泥石流危险性评价[J]. 工业安全与环保, 2016(1): 56-60.

[7] 孙占全, 潘景山, 张赞军, 等. 基于主成分分析与支持向量机结合的交通流预测[J]. 公路交通科技, 2009(5): 127-131.

[8] 姚智胜, 邵春福, 熊志华, 等. 基于主成分分析和支持向量机的道路网短时交通流量预测[J]. 吉林大学学报(工学版), 2008(1): 48-52.

[9] 陈伟根, 滕黎, 刘军, 等. 基于遗传优化支持向量机的变压器绕组热点温度预测模型[J]. 电工技术学报, 2014(1): 44-51.

[10] 吴景龙, 杨淑霞, 刘承水. 基于遗传算法优化参数的支持向量机短期负荷预测方法[J]. 中南大学学报(自然科学版), 2009(1): 180-184.

[11] VAPNIK V N. The Nature of Statistical Learning Theory[M]. New York: Springer-Verlag, 1995: 23-105.

[12] 孙继平, 佘杰. 基于支持向量机的煤岩图像特征抽取与分类识别[J]. 煤炭学报, 2013(S2): 508-512.

[13] 丁世飞, 齐丙娟, 谭红艳. 支持向量机理论与算法研究综述[J].电子科技大学学报, 2011(1): 2-10.

[14] 吴景龙, 杨淑霞, 刘承水. 基于遗传算法优化参数的支持向量机短期负荷预测方法[J]. 中南大学学报(自然科学版), 2009(1): 180-184.

（责任编辑：刘格云）

Debris Flow Risk Prediction Based on PCA-GA-SVM Model

王晨晖，张 超

WANG Chen-hui，ZHANG Chao

河北地质大学 勘查技术与工程学院，河北 石家庄 050031

Hebei GEO University, Shijiazhuang, Hebei 050031

为准确预测泥石流危险度，提出了基于主成分分析法（PCA）和遗传算法（GA）优化的支持向量机（SVM）模型。首先利用主成分分析法对7个泥石流危险度影响因子进行数据降维，将提取出的主成分作为支持向量机模型的输入向量，以泥石流危险度作为输出向量，并运用遗传算法寻优获得最佳支持向量机模型参数，最终建立了基于PCA-GA-SVM的泥石流危险度预测模型，并对9条泥石流沟的危险度进行预测，结果表明：PCA-GA-SVM模型的预测准确率达88.9%，满足工程要求。

泥石流危险度；主成分分析法；遗传算法；支持向量机

In order to predict debris flow risk accurately, support vector machine (SVM) model optimized by genetic algorithm (GA) based on principle component analysis (PCA) was proposed. First, using PCA to make data dimension reduction for 7 influencing factors of debris flow risk, then the extracted principle components were used as model input vectors, and debris risk degree as model output vectors, and the best SVM parameters were optimized by GA, finally the prediction model for debris flow risk based on PCA-GA-SVM was established, and it was used to predict the risk of 9 debris flow gullies. The result shows that the prediction accuracy of PCA-GA-SVM model is 88.9%, which meets general requirements of engineering.

debris flow risk; principal component analysis; genetic algorithm; support vector machine

P642.23

A

1007-6875(2017)02-0020-05

��日期：2017-03-02

10.13937/j.cnki.hbdzdxxb.2017.02.004

河北地质大学第十三届学生科技基金重点科研项目（KAG201607）。

王晨晖（1992—），男，河北邢台人，硕士研究生，主要从事地质灾害治理与防治研究。