六面体体元网格三维地质模型剖切算法①
张文东, 明志强, 刘培刚
(中国石油大学 计算机与通信工程学院, 青岛 266580)
六面体体元网格三维地质模型剖切算法①
张文东, 明志强, 刘培刚
(中国石油大学 计算机与通信工程学院, 青岛 266580)
针对常用的六面体体元网格三维地质模型, 提出了一种求剖切面的算法. 首先, 采用分层投影求交点的方式, 将地质体模型与切割面投影到同一平面, 三维空间下的地质体模型与切割面的剖切转化为二维平面上的四边形网格与切线段求交点的运算. 为减少判交次数, 先根据切线走势判断可能存在交点的区域, 再对可能区域进行精确判交. 其次, 找到并求出不能通过投影方式得到的交点. 然后, 将得到的所有交点按规则组成四边形网格, 对每个四边形三角化处理得到TIN形式的剖切面. 最后, 对该TIN面进行显示. 实验证明了对六面体体元网格三维地质模型剖切的可行性.
三维地质模型; 六面体体元; 剖面切割; 投影法; 不规则三角网
在三维地质体的可视化研究领域, 对地质模型进行剖面切割是一个重要的组成部分. 剖切后生成的剖切面方便分析不透明地质体基本内部构造及属性. 常用的三维地质建模方式有表面模型(主要是TIN模型)、体元模型和混合模型[1]. 不同的建模形式也决定了不同的剖切方法. 文献[2]提出基于TIN数据三维地质体的折剖面切割算法, 提高了算法效率, 但地质体模型基于边界表达, 剖切后形成的剖面不能直观有效的地表现内部构造. 文献[3]提出了基于四面体格网模型的地质体剖面生成算法, 该方法在求边与切面的交点时, 四面体的六个边都要与切面进行判断, 并有重复计算的情况, 降低了执行效率. 文献[4]提出一种基于AutoCAD平台的三维地质实体模型自动生成地质剖面的方法,该方法借助于现有的三维实体模型, 省去大量计算, 但剖切的三维实体模型是已存在的, 缺乏灵活性. 文献[5,6]引入虚拟现实中碰撞检测包围盒的方法, 可以有效的减少求交次数, 但包围盒树的构建与存储相对复杂. 文献[7,8]提出基于八叉树的快速构建三维地质剖面的算法, 该算法在一定程度上提高了切割效率, 降低时间复杂度. 本文提出六面体体元网格三维地质模型剖切方法, 被剖切的地质体模型是由多个六面体体元组成, 每个体元又由8个相邻原始地质数据点按一定规则组成,如图1所示, 剖切时切割面会与各六面体体元的边相交,采用分层投影求交点的方式求出各交点, 所有交点所构成的平面就是所求剖切面. 通过此方法得到的剖面可更准确客观地表达模型内部结构.

图1 三维坐标系下的地质模型
1 算法说明
实现三维地质模型的剖切, 首先要确定三维地质模型, 选择合适的切割面并进行剖切处理, 最后将剖切面三维显示. 本文使用六面体体元网格的地质体模型,该模型是一种结构化的体元模型, 基本结构是一系列六面体, 每个体元由8个数据点组成且有独立的描述和存储. 与四面体模型相比, 六面体在达到模型要求精度所用的节点数及网格数明显少于四面体模型[9]. 图2为三维地质剖切整体流程图. 本文将重点放在剖切面的生成上.
将地质体模型置于三维笛卡尔坐标系X-Y-Z中, 如图1所示, 用X方向表示地质体长, Y方向表示地质体宽,Z方向表示地质体深. 因为生成地质体模型的数据个数是已知的, 所以每个具体的地质体模型X, Y, Z三个方向上数据点的个数是确定的, 根据数据点个数可算出每个方向上六面体体元数量. 假定在Z轴方向有k个有效数据点, 说明在深度上有(k-1)层六面体体元, X轴方向若有i个数据点, 地质体长度上就有(i-1)层六面体体元, Y轴方向若有j个数据点, 宽度方向就有(j-1)层六面体体元.

图2 三维地质模型剖切流程图
2 算法步骤
实际的三维地质体模型多由非规则六面体体元组成, 图3为P1、P2、P3、P4、P5、P6、P7、P8八个数据点组成的单个体元剖切情况图, 六个面的大小不同.当剖切面为四边形A’B’C’D’时, 切面只与体元的顶面或底面相切, 使用投影求交点. 当剖切面为四边形ABCD, 出现剖切面与体元侧面相切的情况, 图中点E为侧面交点无法通过投影获取, 需要单独计算.
2.1 分层投影求交
进行分层投影求交, 分别将切割面与被切割地质体投影到二维X-0-Y面上(算法中用到的切割面要求不与平面X-0-Y平行), 分层投影次数由地质模型在Z轴方向的六面体体元层数决定, 每次投影后三维地质体变成只保留长和宽的四边形网格结构, 切割面变成一条线段, 把该线段记为L. 求三维剖切面变成二维上求线段与四边形各边交点的运算.

图3 单个体元剖切图
图4为一次投影结束后四边形网格与线段L相交情况. 假设地质体在Z轴方向有(k-1)层六面体体元, 每次投影后的平面是(i*j)个顶点组成的四边形网格, 就会有(i-1)*(j-1)个四边形, 每个四边形四条边分别记为:P1P2、P2P3、P3P4、P4P1.

图4 地质体模型与切割面投影后的二维形式
投影求交具体步骤为:
(1) 地质体模型与切割面完成一次投影, 分别得到四边形网格与线段L.
(2) 从网格坐标原点起始位置开始每次选择一个四边形, 让其四条边分别与线段L判交. 如果边P1P2与线段L有交点, 首先在二维空间下求出平面坐标(X, Y),然后映射回三维空间下求出三维交点坐标(X, Y, Z). 已知三维空间两点坐标P1、P2, 设点P1为(Xp1, Yp1, Zp1),点P2(Xp2, Yp2, Zp2), 由空间直线两点式方程可求出过P1、P2的直线方程.

因为交点坐标过空间直线方程P1P2, 将二维空间求得的交点坐标(X, Y)带入公式(1)可求出三维交点坐标(X, Y, Z). P2P3、P3P4、P4P1依次与线段L判交, 并记录每次的交点坐标.
(3) 选择下一个四边形并判断其合法性, 若没有超出网格四边形总个数(i-1)*(j-1), 执行该四边形与线段L的判交操作, 超出就退出本次投影求交.
(4) 对地质模型体元结构进行下一层的投影, 判断是否超出Z轴方向总层数(k-1), 若没有超出继续执行步骤(2)(3), 否则就退出全部投影求交.
2.2 投影求交优化
如果线段L依次与网格上每个边进行判交, 判交次数过多. 在实际的剖切过程中, 切割面不会与地质模型的所有边都有交点, 找出可能存在交点的区域以缩小判交范围. 因此在传统判交基础上进行了改进, 减少不必要的求交判断以提高效率.
在切割面与平面X-0-Y不平行的前提下, 投影后地质体模型与切割面的关系会有图5(a)(b)(c)三种情况,切割面投影后形成的线段L的斜率依次为负值、正值和零. 可在每次判交前确定线段L的斜率, 根据斜率确定判交的方向走势.

图5 投影后地质模型与切割面3种关系图
对图5(a)的情况, 先确定第一个交点所在四边形位置, 标记该交点出现在X轴方向本行第m1个四边形上;计算线段L斜率, 这里为负值, 可初步判断下次出现交点的四边形只能是下一行第m1个或m1之后的位置;Y轴方向行数加1, 新行的判交从该行第m1个四边形开始, 忽略m1之前的判交操作. 标记新行出现交点的四边形为第m2个; 依次类推执行至结束. 图5(b)的情况, 首先找到第一个交点出现的四边形, 标记该交点出现在X轴方向本行第n1个四边形上; 计算线段L斜率, 这里为正值, 可初步判断下次出现交点的四边形只能是第n1个或n1之前的位置; 行数加1, 新行的判交操作从第n1个开始依次往前递减执行, 忽略第n1个之后的判交.标记新行出现交点的四边形为第n2个; 依次类推执行至结束. 图5(c)的情况, 首先找到第一个交点同样标记位置; 计算线段L斜率, 这里为1; 此种情况所有交点坐标的X值相同, 按顺序求出对应不同Y值与Z值即可.
除去地质模型最后一层, 其他各层六面体体元底层与相邻下一层的顶层由相同的顶点组成, 因此每次投影后选择只对每个体元结构的顶面判交. 再加上最后一层体元结构的底面判交结果.
2.3 计算侧面交点
在每层投影求交时记录各交点出自该层哪一个四边形, 四边形用索引值区分. 图3中顶面M与底面M’有相同索引值, 顶面M中有交点A、B、A’、B’, 底面M’有交点C’、D’, 交点C、D落在M’之外, 此时体元出现与侧面相切.
P2、P6为已知数据点, 设点P2为(Xp2, Yp2, Zp2),P6(Xp6, Yp6, Zp6), 由空间直线两点式方程(2)确定过P2、P3的直线方程.

投影求交时得到A、B、C、D坐标值, 取其任意三点唯一确定平面ABCD. 设点A(Xa, Ya, Za), B(Xb, Yb, Zb),C(Xc, Yc, Zc). 已知三点不在同一直线, 由空间平面三点式方程(3)求出过A、B、C三点的平面方程. 联立方程(2)与方程(3)求出交点E.
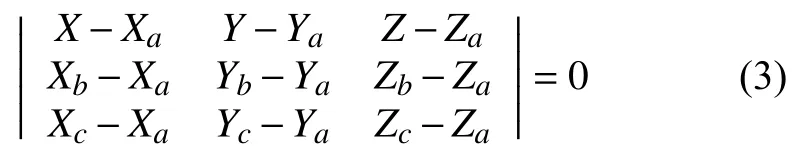
2.4 生成剖切面
判交结束得到投影层及侧面交点坐标, 将各交点坐标按一定规则相连得到要求的剖面. 如图6所示, 第t(1<=t 对四边形网格中每个四边形进行三角化处理[10],每个四边形分割为两个三角形, 如图7, 四边形P1’P2’P3’P4’可转化为三角形P1’P3’P2’和三角形P1’P4’P3’. 最终将四边形网格形式的剖切面转化成三角面片网格形式的剖切面, 方便剖切面三维显示. 图7 四边形三角化转换图 为验证算法的可行性及剖切效率, 使用本算法中六面体体元模型和文献[3]中四面体格网模型分别实现某地区地质体的三维显示并剖切, 切面投影后切线斜率为负值. 实验涉及到的硬件配置为: 操作系统windows7旗舰版, CPU主频2.2 GHz, 安装内存4 G(3.5 G可用). 两种方式都能获得近似一致的地质模型及剖切面. 图8(a)为六面体体元网格生成的三维地质模型,8(b)为生成的地质剖切面. 由实验效果图可知利用该方法可以准确的得到剖切面. 图8 实验效果图 由表1的实验结果可知, 六面体体元网格地质模型在剖切时间上明显比四面体格网模型地质体剖切时短,且数据点个数越多, 效果越明显. 表1 两种地质模型组织方式剖切时间比较 本文针对六面体体元网格的实体地质模型求剖切面. 结合该模型的特点在求交时主要使用了分层投影求交点的方法, 并对特殊切点进行了专门处理, 通过实验证明了此方法的可行性. 另外本算法在剖切时通过对切线走势进行预判断以及投影求交的方式与文献[3]中四面体格网模型的地质体剖切相比, 减少了判交次数, 提高了整体剖切效率. 本次求出的剖切面只以同一颜色进行了三维显示. 由于每个体元的属性可以被独立描述和存储, 每个原始数据都有自己的属性值, 而判交得到的新数据点属性值可根据邻近原始数据点获得, 不同属性值又可用不同颜色区分. 后期为更有效地展现体元网格剖切的优势, 会将每个数据点属性值应用到三维显示上, 得到一个用不同颜色值区分不同属性区的三维地质剖切面. 1刘苏. 三维地质模型可视化方法及应用. 中国高新技术企业, 2015, (30): 133–134. 2明镜, 潘懋, 屈红刚, 等. 基于TIN数据三维地质体的折剖面切割算法. 地理与地理信息科学, 2008, 24(3): 37–40. 3沈敬伟, 周廷刚, 刘德儿, 等. 一种基于四面体格网模型的地质体剖面生成算法. 西南大学学报(自然科学版), 2014,36(8): 123–129. 4刘光伟, 白润才, 吕进国, 等. 基于三维地质实体模型生成地质剖面图的应用. 辽宁工程技术大学学报(自然科学版),2010, 29(4): 557–559. 5李运锋, 刘修国. 基于方向包围盒投影转换的轮廓线拼接算法. 计算机应用, 2011, 31(12): 3353–3356. 6李伟波, 刘嘉, 陈耀华. 三维地层Tin模型剖切的改进算法.计算机应用与软件, 2013, 30(8): 158–161,169. 7赵龙, 闵世平, 代强玲. 基于八叉树的三维地质剖面生成算法. 计算机工程, 2014, 40(2): 250–255. 8Delamé T, Roudet C, Faudot D. From a medial surface to a mesh. Computer Graphics Forum, 2012, 31(5): 1637–1646.[doi: 10.1111/cgf.2012.31.issue-5] 9任辉龙, 巩生龙, 蔡永昌. 基于投影法三维模型全六面体网格的划分方法. 计算机辅助工程, 2013, 22(5): 122–128. 10邹新龙, 石丹, 刘茂, 等. 简单多边形的三角化算法. 环境技术, 2014, (增刊): 137–140. Hexahedral Voxel Grid 3D Geological Model Partitioning Algorithm ZHANG Wen-Dong, MING Zhi-Qiang, LIU Pei-Gang In view of the common hexahedral voxel grid 3D geological model, we introduce a 3D geological model partitioning algorithm. In the process of cutting, the cut surface will intersect with the edge of the hexahedral element.Firstly, the geological model and the cut plane are projected into the same 2D plane at the same time, the process of portioning between geological model and cut plane in the 3D is converted to an operation that looks for the intersection point between the line and the quadrilateral grid. In order to reduce the number of judgement intersections, we would find out the possible intersection area by the Line slope direction of cutting plane, then judge whether there is an intersection carefully. Next, we find other points of intersection that could not be got by projection, and connect the node coordinates according to certain rules form the quadrilateral grid and triangulation. Finally, we display the TIN. Experimental results prove that this method is feasible. three-dimensional geological model; hexahedral voxel; profile cutting; projection method; TIN 张文东,明志强,刘培刚.六面体体元网格三维地质模型剖切算法.计算机系统应用,2017,26(7):195–199. http://www.c-s-a.org.cn/1003-3254/5858.html 2016-10-27; 收到修改稿时间: 2016-12-12
3 算法实验


4 结语
(College of Computer and Communication Engineering, China University of Petroleum, Qingdao 266580, China)

