基于直接横摆力偶矩控制的中置轴汽车列车操纵稳定性研究*
任泽凯张京明张浩董金松张红卫
(1.交通运输部公路科学研究院,运输车辆运行安全技术交通行业重点实验室,北京 100088;2.哈尔滨工业大学,威海 264209)
基于直接横摆力偶矩控制的中置轴汽车列车操纵稳定性研究*
任泽凯1,2张京明2张浩1董金松1张红卫1
(1.交通运输部公路科学研究院,运输车辆运行安全技术交通行业重点实验室,北京 100088;2.哈尔滨工业大学,威海 264209)
建立了中置轴汽车列车4自由度参考模型及多自由度非线性仿真模型,并通过单移线实车试验验证了模型的正确性。利用模糊控制和PID控制方法建立了中置轴汽车列车横摆力偶矩控制(DYC)模型,通过TrukSim及Simulink建立了联合仿真平台,并进行不同附着系数路面上单移线仿真。仿真结果表明,施加DYC后,列车低附着系数路面横摆角速度后部放大系数和质心侧偏角后部放大系数分别减小26.5%、29.9%,最大铰接角速度减小18.4%,大幅改善了中置轴汽车列车的操纵稳定性,降低了折叠事故发生的可能性。
1 引言
GB 1589—2016中首次明确提出了中置轴汽车,中置轴汽车列车是我国货运列车向模块化较长货车列车方向发展的重要环节,在不久的将来必将得到广泛应用[1]。目前国内对中置轴汽车列车的研究尚少,因此,有必要对其操纵稳定性进行前瞻性研究,促进主动控制技术在交通运输领域的发展,确保运输安全。
汽车列车是多辆单车的组合,与单车相比较,运动自由度更多,运动状态更加复杂,容易出现“折叠”“摆振”等失稳现象[2]。受列车后部放大系数的影响[3],列车在高速行驶过程中变换车道时,更容易出现“挂车甩尾”“侧翻”等事故,严重影响运输安全。除在结构上对列车参数进行优化以提高其操纵稳定性外,还可以通过增加主动控制技术确保其运行安全[4~6]。
2 模型建立
2.1 参考模型建立
根据汽车动力学理论,对中置轴汽车列车进行简化。不考虑俯仰运动、侧倾运动及各向载荷转移,不考虑牵引销(环)处的垂直载荷及阻尼,假设轮胎侧偏特性处于线性区域,中置轴挂车双轴相距很近,可以简化为单轴,忽略空气阻力及滚动阻力,得到中置轴汽车列车单轨4自由度模型,如图1所示。
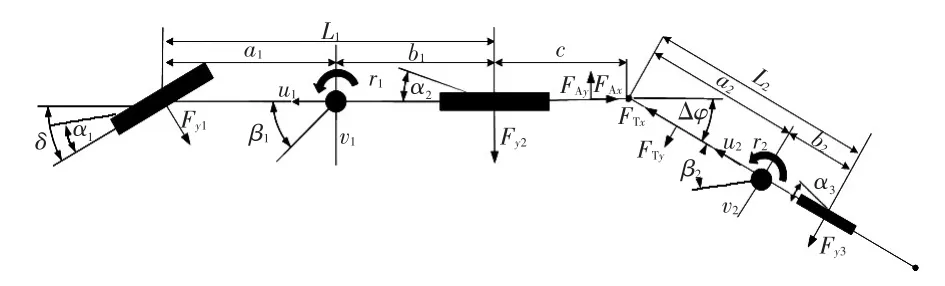
图1 中置轴汽车列车单轨模型
相比于普通半挂汽车,中置轴汽车列车的铰接点位于牵引车后桥之后,铰接点处垂直载荷很小,可以忽略除纵向力、侧向力以外的各向力和力矩,则牵引销处受力对整车横摆运动产生的力矩为FAy(b1+c),其对牵引车横摆运动产生的影响较半挂车大很多。因此,牵引车横摆运动方程为:
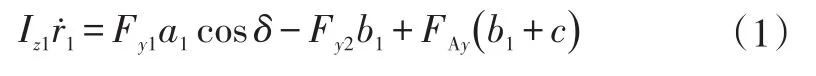
中置轴挂车的另一个特点是其质心靠近车轴处,牵引销处承载的垂直载荷比半挂车小得多,因此,中置轴挂车的横摆运动方程为:
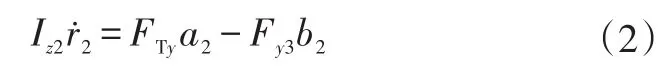
牵引车、中置轴挂车侧向运动方程为:

式中,r1、r2分别为牵引车和挂车的横摆角速度;m1、m2分别为牵引车和挂车的质量;u1、u2分别为牵引车和挂车的纵向速度;Iz1、Iz2分别为牵引车和挂车绕Z轴的转动惯量;a1、b1分别为牵引车质心到前轴和后轴的距离;a2、b2分别为中置轴挂车质心到牵引环和车轴的距离;Fy1、Fy2、Fy3分别为第1轴、第2轴、第3轴车轮的侧向力;FAy、FTy分别为牵引销和牵引环所受的侧向力;c为牵引销到牵引车后轴距离;β1、β2分别为牵引车和挂车的质心侧偏角;δ为转向轮转角。
假定轮胎侧偏特性为线性特性,则
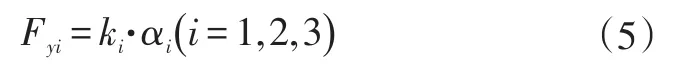
牵引车和中置轴挂车速度耦合方程为:
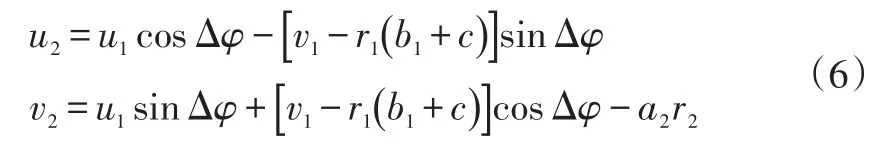
式中,v1、v2分别为牵引车和挂车侧向速度。
牵引车和中置轴挂车铰接点力耦合方程为:
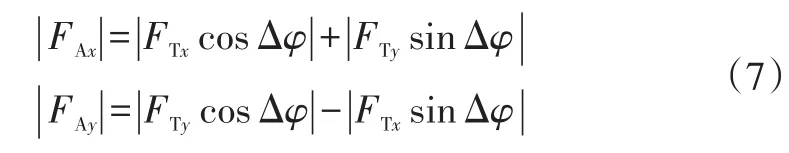
列车铰接角为牵引车和中置轴挂车车身纵线所成的夹角,受车厢尺寸的限制,本文研究的中置轴汽车列车的铰接角较半挂汽车列车小,其满足:

当Δφ、δ很小时,cosΔφ=1,sinΔφ=0,cosδ=1,则
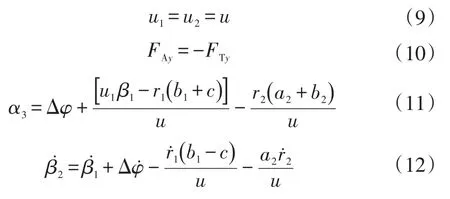
可得运动微分方程:
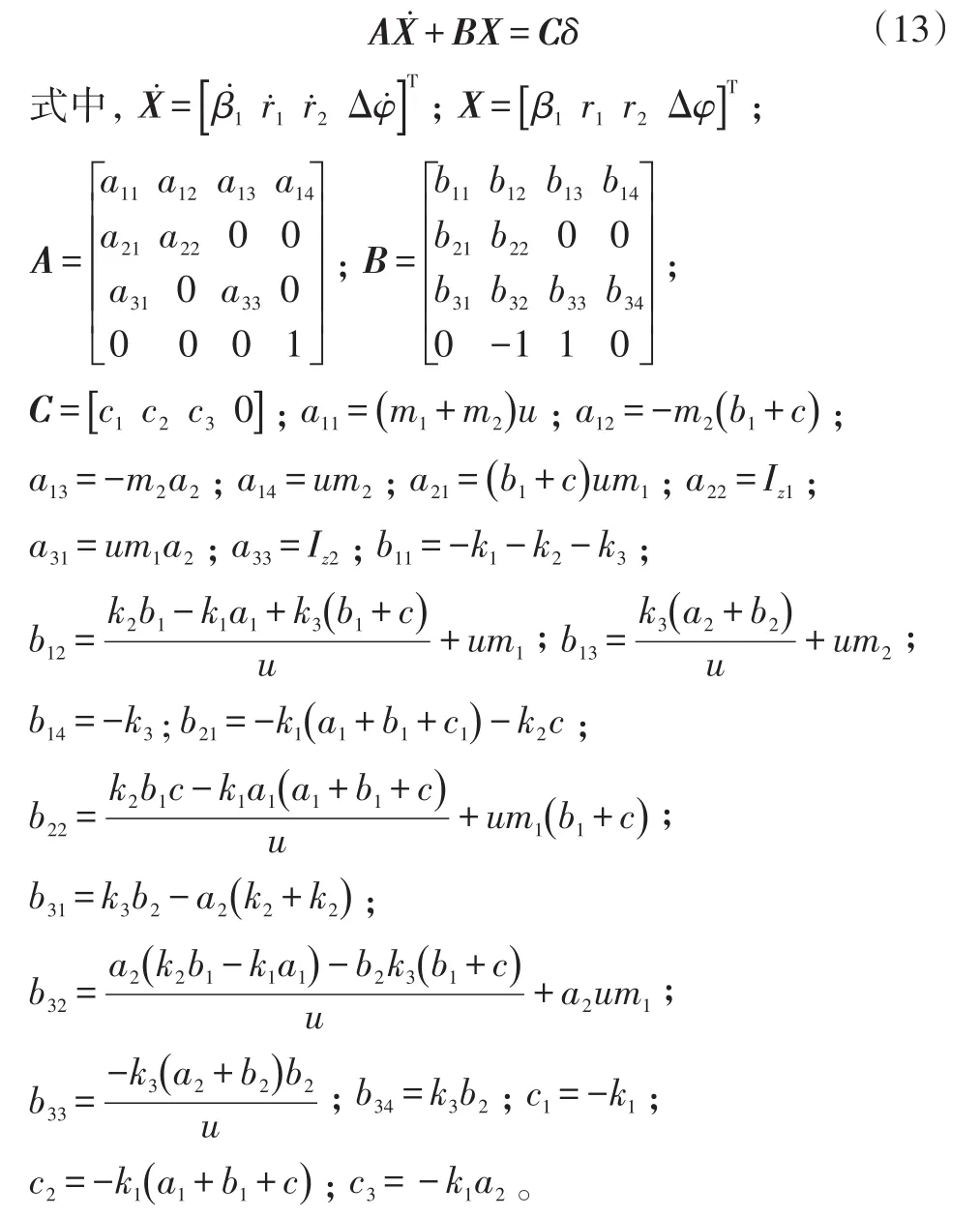

同时,考虑路面附着系数[7]须满足

式中,μ为路面附着系数。
则参考横摆角速度为:
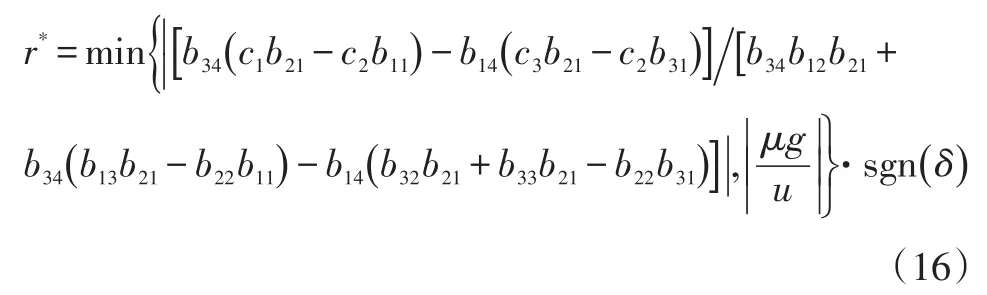
2.2 非线性仿真模型建立
采用汽车动力学仿真软件TruckSim建立多自由度非线性仿真模型,中置轴汽车列车的基本仿真参数如表1所示。

表1 中置轴汽车列车仿真参数
3 仿真模型的实车验证
根据GB/T 25979的要求对试验样车开展单移线试验。试验在列车满载状态下进行,转向盘输入为频率0.25 Hz的正弦信号,试验车速为80 km/h,试验样车如图2a所示,相关参数见表1。利用VBOX数据采集系统检测列车运行状态,RT陀螺仪安装在底盘横梁处,如图2b所示。


图2 试验样车及测试设备
利用VBOX、RT陀螺仪等设备检测列车的横摆角速度、质心侧偏角等关键指标,并利用前述TruckSim和Simulink仿真模型进行仿真验证,试验与仿真结果如图3所示。
对比实车试验和仿真的结果可以看出,反映中置轴汽车列车主要特性的关键参数变化趋势一致,吻合情况较好。因此,所建立的中置轴汽车列车仿真模型能够反映列车的响应特性,从而验证了理论模型的正确性及仿真模型的可靠性。
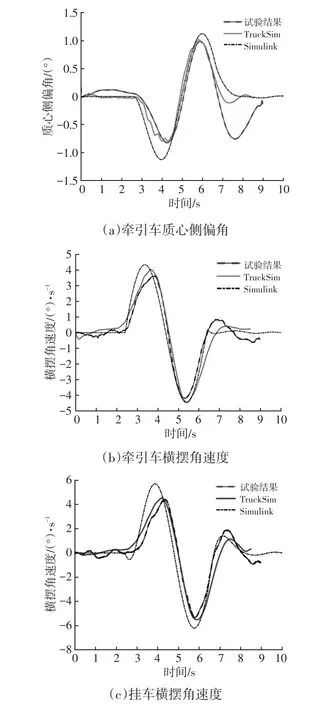

图3 试验与仿真结果
4 横摆力偶矩控制策略
中置轴汽车列车横摆力偶矩控制(Direct Yaw moment Control,DYC)原理如图4所示。设计原则是使牵引车横摆角速度跟随参考值,同时尽量降低铰接角速度以减小后部放大系数。采用模糊控制的方法动态调节DYC介入的门限。通过PID控制器计算所需制动力矩,并结合控制门限值最终确定实际输出制动力矩。通过制动力分配策略,控制列车某车轮进行制动(忽略侧向力的影响),以提供相应的横摆力偶矩,改善汽车列车的行驶稳定性。联合仿真顶层模型如图5所示。
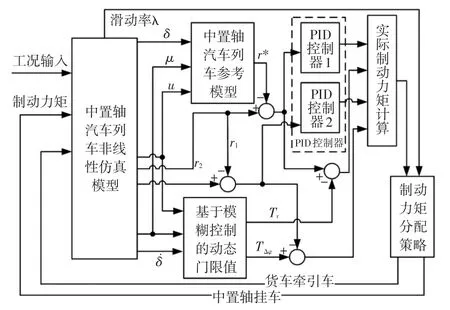
图4 横摆力偶矩控制原理
4.1 基于模糊控制的DYC介入门限策略
在不同车速、路面附着条件、车轮转角速度条件下,DYC介入的时机应不同[8]。本文利用模糊控制器,设计了不同工况下的DYC介入门限。控制器的输入信号为车速u、路面附着系数μ、车轮转角速率δ̇,输出值为横摆角速度偏差门限Tr和铰接角速度门限TΔφ。当实际横摆角速度与参考横摆角速度偏差大于Tr或铰接角速度大于TΔφ时,控制系统介入。
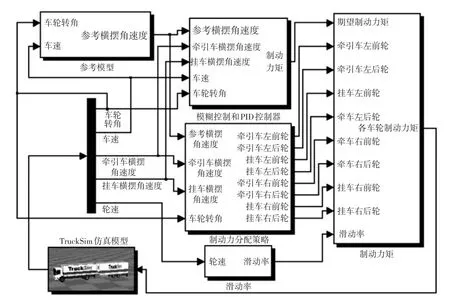
图5 联合仿真顶层模型
u的基本论域为[0,100],量化因子取100。μ的基本论域为[0,1],量化因子取1。δ̇的基本论域为[0,2.5],量化因子取2.5。Tr的基本论域为[0,0.05],比例因子取0.05。TΔφ的基本论域为[0,0.03],比例因子取0.03。模糊控制器输入、输出变量隶属度函数及模糊集合如图6所示,模糊规则如表2所示。
4.2 PID制动力矩计算模型
PID控制通过调节相关参数可以实现对目标对象良好的跟踪。汽车DYC通常以稳态横摆角速度响应作为跟踪对象。对于中置轴汽车列车而言,还应尽量减小铰接角速度,以降低后部放大系数,避免折叠事故,保持列车的稳定性。因此,本文选取由式(16)确定的参考横摆角速度作为货车牵引车的跟踪目标,选取铰接角速度作为中置轴挂车的跟踪目标,建立2个PID控制器计算DYC中所需的制动力矩。货车牵引车PID控制器的比例系数、积分时间常数、微分时间常数分别取0.85、0.20、0.45,中置轴挂车PID控制器的比例系数、积分时间常数、微分时间常数分别取0.80、0.30、0.40。


图6 模糊控制器输入输出隶属度函数
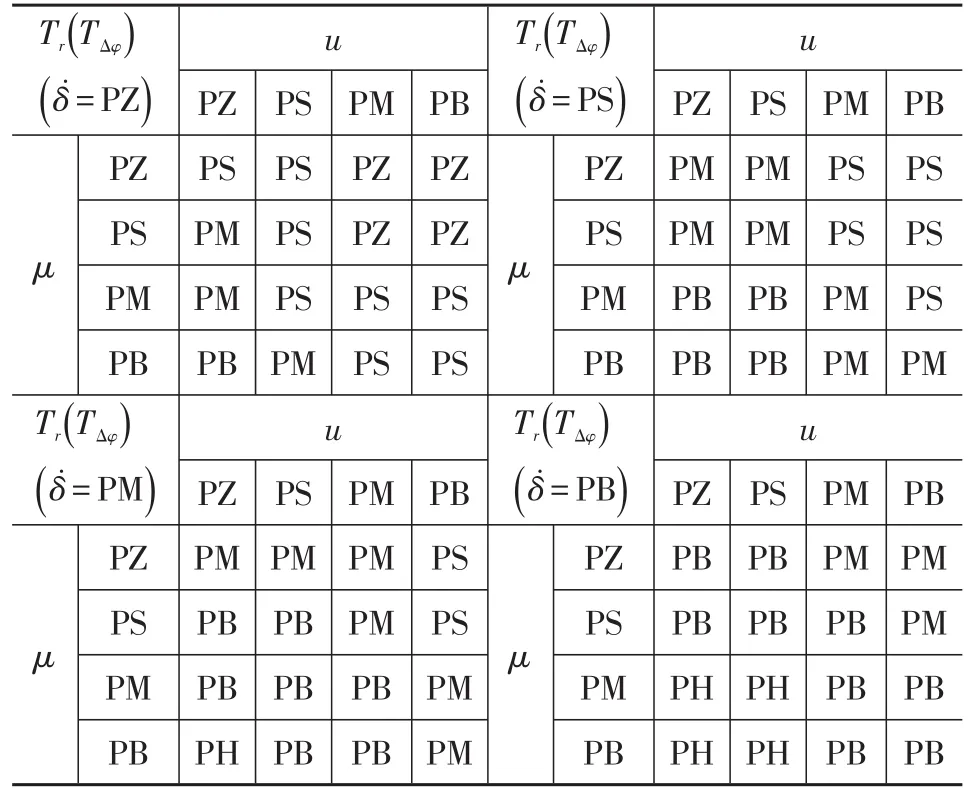
表2 模糊逻辑规则
4.3 制动力分配策略
不同车轮施加制动对DYC产生的效果不相同[9],对两轴货车牵引车的前外轮和后内轮施加制动力所产生的DYC效果最明显。DYC制动力分配方案除考虑横摆角速度外,还应考虑驾驶员的转向意图[10]。因此,本文增加了车轮转角速率δ̇作为参考,制定货车牵引车制动力分配策略如表3所示,其中,“+”“-”表示该值的符号。
根据GB 1589—2016的要求,中置轴挂车的质心应紧靠车轴。因此,可以认为对中置轴挂车同侧车轮施加制动力所产生的DYC具有相同的效果。传统单车DYC的输入信号通常为横摆角速度和质心侧偏角,考虑到影响汽车列车操纵稳定性的重要因素之一是铰接角速度,且本文研究的中置轴汽车列车中的中置轴挂车大部分载荷由挂车单独承担,对牵引货车的影响较小,故本文对中置轴挂车进行横摆力偶矩控制的目标是尽量减小铰接角速度。所以当铰接角速度大于0时,控制挂车左侧车轮;小于0时,控制挂车右侧车轮;等于0时,不对挂车车轮施加控制。
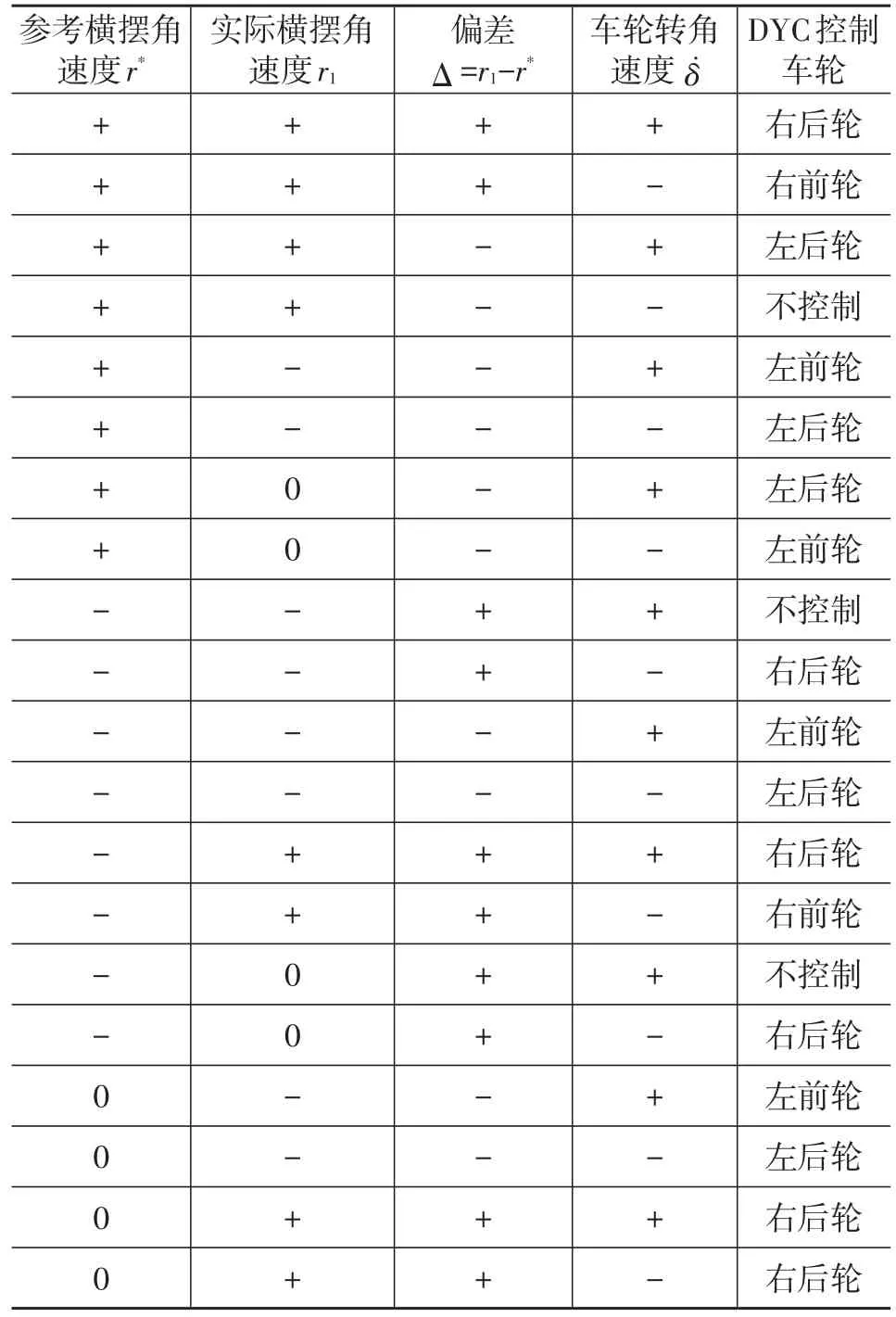
表3 货车牵引车制动力分配方案
为了防止车轮制动发生抱死,设定各车轮滑动率不超过0.25。
5 仿真分析
以本文建立的联合仿真模型为平台,选取单移线试验进行仿真,以横摆角速度、质心侧偏角等为指标,分析中置轴汽车列车DYC对汽车列车操纵稳定性的影响。低路面附着系数取0.4,高路面附着系数取0.8,移线宽度为3.5 m,仿真车速为80 km/h。仿真结果见表4及图7~图13。
图7所示为单移线试验轨迹仿真结果,其中,X、Y与整车坐标系方向一致。由表4和图7可以看出,施加DYC后,列车跟随目标轨迹效果更好,牵引车和中置轴挂车超调量明显减小。相比于高附着系数路面,不施加DYC的列车在低附着系数路面的轨迹超调量明显增大,调节时间也明显增加,而施加DYC后则有很大改善。

表4 单移线仿真结果
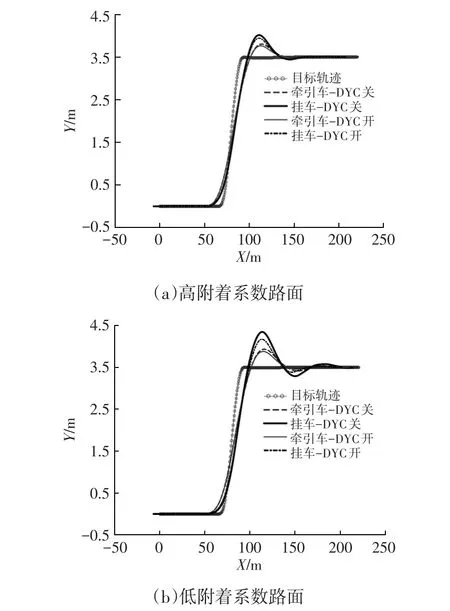
图7 单移线试验轨迹
图8所示为列车在两种附着系数路面上横摆角速度响应。可以看出,施加DYC后能明显降低牵引车和中置轴挂车的横摆角速度峰值,缩短进入稳态所需的时间,对挂车的横摆角速度改善尤为明显。由于路面附着系数降低,中置轴挂车的横摆角速度响应后部放大效果更加明显,较大的后部放大系数严重影响列车高速行驶稳定性[3]。施加DYC后,列车在低附着系数路面上的横摆角速度后部放大系数降低26.5%,这对提高列车的稳定性有重要意义。
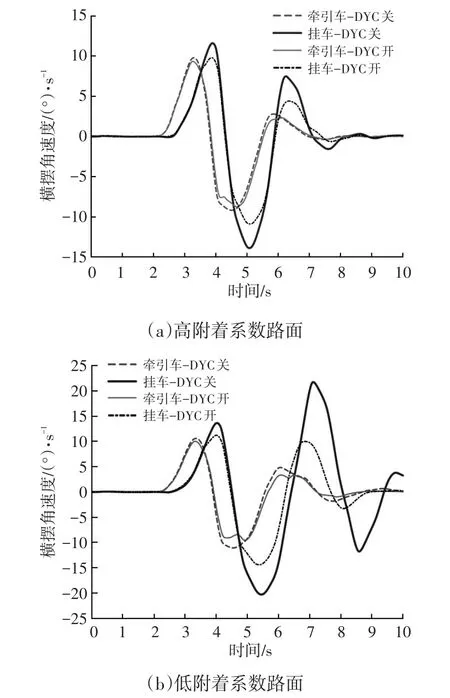
图8 横摆角速度响应
图9所示为列车铰接角速度在高、低附着系数路面上的仿真结果。铰接角速度是汽车列车须考虑的重要因素[11]。可以看出,在低附着系数路面上,列车铰接角速度幅值增加且振荡周期加长,极易造成折叠、侧翻事故。施加DYC后,列车的铰接角速度幅值大幅减小,低附着系数路面上改善效果达18.4%,且能快速进入稳定状态,大大降低了折叠事故发生的可能性,提高了列车稳定性。
质心侧偏角是影响汽车操纵稳定性的重要指标[12],其仿真结果见图10。由图10可以看出,施加DYC后,中置轴汽车列车质心侧偏角均明显减小,且响应更加迅速。在低附着系数路面上,质心侧偏角后部放大系数降低29.9%,这有利于及时调整列车运行方向,提高汽车列车的操纵性能。

图9 铰接角速度响应
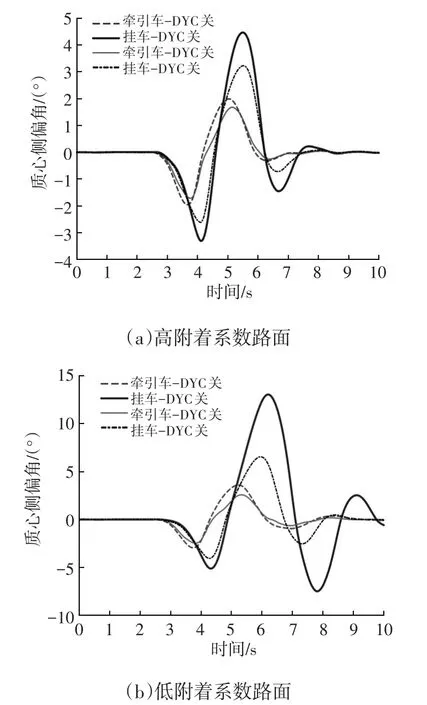
图10 质心侧偏角响应
侧倾角虽然不是汽车横摆力偶矩控制的直接对象,但由于汽车列车整体稳定性能得到提高,牵引车和中置轴挂车的侧倾角幅值也得到一定程度的降低,如图11所示,说明车身稳定性控制系统在一定程度上也能改善汽车抗侧翻性能[13]。
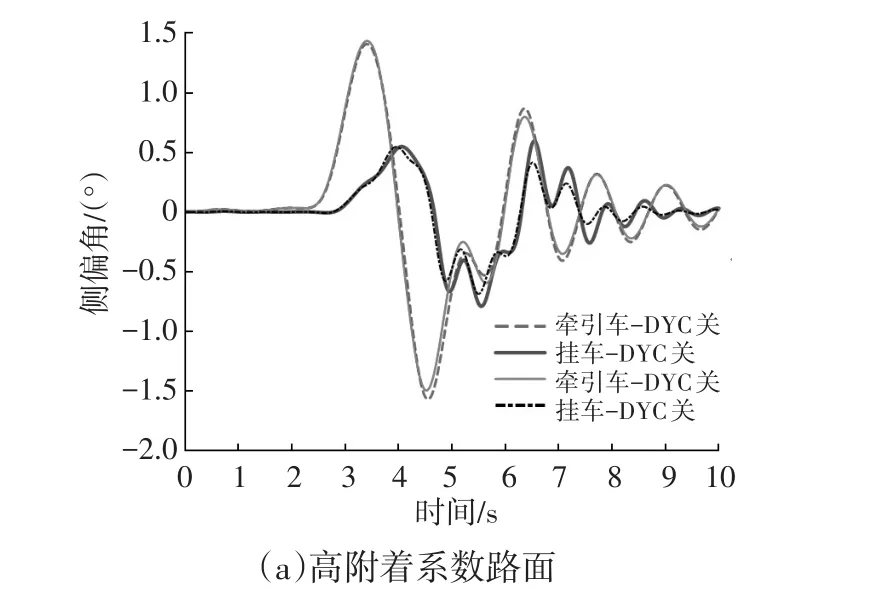

图11 侧倾角响应
车轮制动力矩仿真结果如图12所示。由图12可以看出,在列车运动状态变化较大的第4 s~第6 s,PID输出制动力矩较大,以便纠正列车姿态。此后列车趋于稳定状态,PID输出制动力矩较小。低附着系数路面上各轮制动更加频繁,以不断调整列车姿态。图13显示了中置轴汽车列车各车轮的滑动率。在高附着系数路面上,各车轮滑动率都很低,没有发生抱死,控制效果较好。在容易发生车轮抱死的低附着系数路面上,最大滑动率维持在目标值附近,车轮没有出现抱死,保证了良好的附着性能。
6 结束语
本文建立了中置轴汽车列车动力学模型,并通过实车试验验证了模型的正确性,为中置轴汽车列车的理论研究提供有益参考。以车速u、路面附着系数μ、车轮转角速率δ̇为输入,横摆角速度偏差门限和铰接角速度门限为输出,设计了中置轴汽车列车DYC介入门限策略,有利于DYC适应多种工况。同时,设计了货车牵引车和中置轴挂车在施加DYC时采用的制动力分配方案。通过仿真验证了所建立的DYC模型的有效性,较好地改善了中置轴汽车列车的操纵稳定性。下一步可以考虑横摆力偶矩控制和汽车列车ABS的集成控制,并考虑响应时间的影响,促进研究成果进一步实用化。

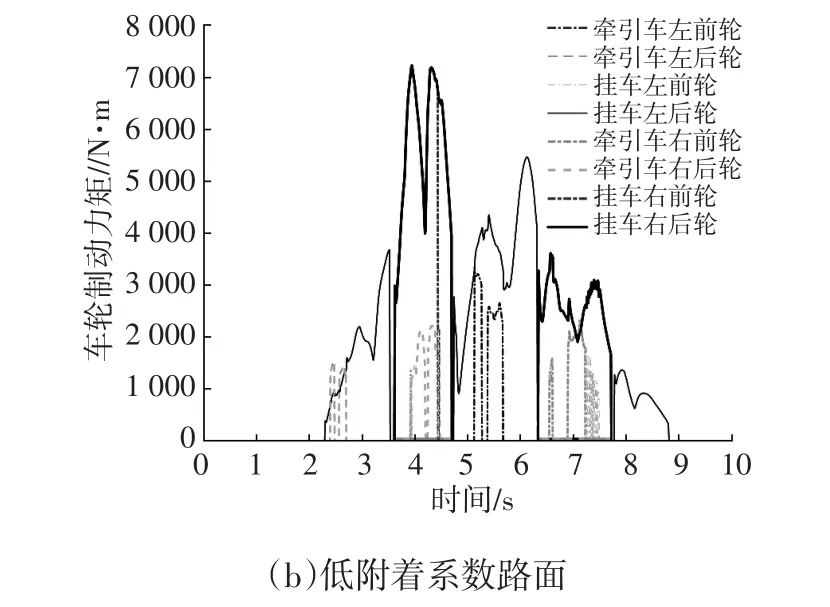
图12 车轮制动力矩

图13 各车轮滑动率
1 马增荣.中置轴货车列车-商品车公路运输未来的主流装备.物流技术与应用(货运车辆),2009(3):66~68.
2 Fayed M A E E,Ghany M A.Simulation of tractor semitrailer manoeuvre at high speed using MATLAB/ SIMULINK.InternationalJournalofHeavy Vehicle Systems,2011,18(4):341~358.
3 Dahlberg E,Stensson A.The dynamic rollover threshold-a heavy truck sensitivity study.International Journal of Vehicle Design,2006,40(1~3):228~250.
4 Hac A,Fulk D,Chen H.Stability and Control Considerations ofVehicle- Trailer Combination.Sae International Journal of Passenger Cars Mechanical Systems,2009,1(1):925~937.
5 Nagai R.Stabilization of Passenger Car-Caravan Combination Using Four Wheel Steering Control.Vehicle System Dynamics,1995,24(24):313~327.
6 Fernández M A A,Sharp R S.Caravan Active Braking System-Effective Stabilisation of Snaking of Combination Vehicles.Automotive and Transportation Technology Congress and Exposition,Barcelone,2001.
7 于志新,宗长富,何磊,等.基于LQR的重型半挂汽车列车稳定性控制策略.中国公路学报,2011,24(2):114~119.
8 李寿涛,马用学,郭鹏程,等.一种变逻辑门限值的车辆稳定性控制策略研究.汽车工程,2015(7):782~787.
9 Yamamoto M,Koibuchi K,Fukada Y,et al.Vehicle stability control in limit cornering by active brake.Jsae Review,1995,16(3):323.
10 余卓平,高晓杰,张立军.用于车辆稳定性控制的直接横摆力矩及车轮变滑移率联合控制研究.汽车工程,2006,28(9):844~848.
11 韦超毅.拖挂式房车列车操纵稳定性研究:[学位论文].镇江:江苏大学,2008.
12 王德平,郭孔辉,宗长富.车辆动力学稳定性控制的理论研究.汽车工程,2000,22(1):7~9.
13 金智林,翁建生,胡海岩.汽车侧翻预警及防侧翻控制.动力学与控制学报,2007,5(4):365~369.
(责任编辑 斛 畔)
修改稿收到日期为2017年3月13日。
Research on Handling Stability of Centre Axle Trailer Train Based on Direct Yaw Moment Control
Ren Zekai1,2,Zhang Jingming2,Zhang Hao1,Dong Jinsong1,Zhang Hongwei1
(1.Key Laboratory of Operation Safety Technology on Transport Vehicles,Research Institute of Highway,Ministry of Transport,Beijing 100088;2.Harbin Institute of Technology,Weihai 264209)
Reference dynamic model of centre axle trailer train with 4-DOF and nonlinear simulation model with multi-DOF were established.Single lane change test was carried out to verify the correctness of the models.Direct Yaw moment Control(DYC)model was constructed based on PID and fuzzy control.Single lane change test simulations with different road adhesion coefficients were carried out through the established co-simulation platform based on TruckSim and Simulink.Simulation results showed that DYC could improve handling stability of centre axle trailer train obviously as the rear amplifications for yaw rate and sideslip angle were reduced by 26.5%and 29.9%respectively.The maximum articulated angle rate was reduced by 18.4%and handling stability of centre axle trailer train was improved obviously, decreasing the possibility of jackknifing occurring.
Handling stability,Direct yaw moment control,Centre axle trailer train,Fuzzy control
操纵稳定性;横摆力偶矩控制;中置轴汽车列车;模糊控制
U469.5
A
1000-3703(2017)05-0006-08
交通运输部应用基础研究项目(2014319223020);中央级公益性科研院所基本科研业务费专项资金项目(2015-9019)。

