考虑非理想器件模型的电力电子系统状态方程分析法

凌亚涛 赵争鸣 杨 祎 李帛洋 袁立强

（清华大学电机系 电力系统及发电设备安全控制和仿真国家重点实验室 北京 100084）

考虑非理想器件模型的电力电子系统状态方程分析法

凌亚涛 赵争鸣 杨 祎 李帛洋 袁立强

（清华大学电机系 电力系统及发电设备安全控制和仿真国家重点实验室 北京 100084）

针对目前电力电子仿真软件存在的对功率开关器件电磁瞬态过程仿真不够准确，强刚性电路引起数值仿真计算发散等问题，提出一种基于量化状态系统（QSS）的离散状态事件驱动（DSED）仿真分析方法。该方法需要加入自动识别电力电子系统开关过程以及根据电路拓扑和所处状态自动列写状态方程的相关算法。针对该需求提出一种基于图论方法的状态方程及输出方程提取分析方法。首先，经理论分析得到，将选用的器件模型代入电路可以得到状态方程的标准形式；进而，提出电力电子系统电路的参数结构矩阵程式化列写方法，并基于此方法针对开关电路每一次开关器件切换都需要重新列写状态方程这一特点进行了相关分析。最后，对几个典型电力电子系统电路进行仿真计算，结果证明了该提取分析方法的有效性。

状态方程分析法 器件非理想特性 器件模型 离散状态事件驱动 仿真性能

0 引言

目前，各种商用电力电子仿真软件（如Matlab、PSpice、PSIM等）已经得到广泛应用。但在实际应用中，发现这些仿真软件都存在两个问题：①考虑功率开关器件非理想模型则计算时间非常长；②存在强刚性电路引起数值仿真计算发散。为解决这些问题，作者所在课题组提出了一种基于量化状态系统（Quantized State System, QSS）离散状态事件驱动（Discrete State Event Drive, DSED）仿真分析方法。

DSED方法中的核心数值算法为QSS算法，关于QSS算法的收敛性、准确度、算法稳定性等，已有不少文献进行了研究[1-6]，本文不再赘述。

电力电子系统建模一般是基于等效电路建立状态空间方程组。当采用理想开关模型时，即为二值电阻模型：通态为小值电阻，阻态为大值电阻；当考虑非理想开关模型时，则需采用较复杂的开关等效电路模型。不管采用哪种模型，所建立的电力电子系统模型均为状态空间方程组，如

所采用的核心数值算法QSS仍然为求解一阶常微分方程组（Ordinary Differential Equation, ODE）的算法。由于电力电子系统中电感电容较多，特别在考虑开关器件非理想模型时，电路中的电感电容成倍增加，这给列写独立的状态空间方程组以及构造状态方程的系数矩阵造成很大的麻烦：难以辨别独立状态方程真伪，且人工分析工作量很大。

不少文献就如何系统有序地提取电路独立状态方程给出了各种方案，比较经典的做法是利用网络图论，选取电容电压、电感电流作为状态变量[7-10]。也有方案不依赖图论，如文献[11]基于能量守恒原理，以节点电位和节点电位的积分共同作为状态变量来构造电路的状态方程。虽然给出的状态空间方程的系数矩阵很方便求取，但是为了得到标准形式的状态方程，该方法也需要对一个对称矩阵求逆。此外，在文献[11]提供的方法中，状态变量数为节点数的两倍，并且需要求解出所有节点电位的积分值，没有直接的意义；同时没有考虑电力电子电路中存在互感的情况，没有给出电路所有支路电量输出方程的计算方法或表达式。

为解决在考虑器件非理想模型时自动列写状态方程分析的问题，本文提出一种基于图论方法的状态方程及输出方程提取分析方法，该方法考虑了电路包含所有常见元件（含互感）的情况，也给出了描述电路所有支路电量的输出方程计算方法和表达式。首先对所选用器件模型进行简要介绍，进一步将该折线模型转化为方便提取状态方程的等效子电路形式。然后重点验证在应用器件的非理想模型时，所提的图论分析方法可以获得整个电力电子电路标准形式的状态空间方程和输出方程。本文对该网络分析方法存在的问题也进行了分析归纳，给出了一些解决思路和方法，并在器件非理想特性和线路杂散参数的情况下，分析了典型的电力电子电路仿真波形和仿真性能。最后对所提状态方程提取与分析方法进行了总结。

1 开关器件的非理想模型

以绝缘栅双极型晶闸管（Insulated Gate Bipolar Transistor, IGBT）器件非理想模型为例，在实现的方便性和结果的准确性两者之间折中，选择该器件的行为模型[12-14]。本文对IGBT的三端电容模型和折线模型这两种行为模型进行分析。

1.1 IGBT三端电容模型

IGBT三端电容行为模型如图1所示[14]。它将IGBT开通和关断瞬态过程各划分为五个阶段，在各个阶段内，这些元件值均为常数。但Rge、Cgc、Rce这三个元件在不同阶段有不同的取值，如栅极电阻值Rge在关断瞬态一般大于开通瞬态。Imos为栅极MOS电流，表达式为

式中，Vth为IGBT阈值电压；KP为计算系数。式（2）三个式子依次表征IGBT工作在截止、饱和、放大区。

图1 IGBT的三端电容行为模型Fig.1 Three-terminal capacitor behavioral model for IGBT

1.2 IGBT折线模型

图2为IGBT关断过程中的折线模型，其中，vce为IGBT与二极管换流时的端电压；ic为集电极电流；vge为栅射极电压；Vcesat、VDC、Vmax、Vg(on)、Vg(off)、Vml、Vth、IL、Itail分别为通态饱和压降、断态承压、关断尖峰电压、栅极开通、关断电压、米勒电压、阈值电压、负载电流和拖尾电流；t0～t5为6个时间节点；三条曲线（vce、ic、和vge）以各节点之间的线性、常数或指数衰减的形状表征。

图2 IGBT关断过程的折线模型Fig.2 Piecewise linear behavioral model for IGBT’s turn-off transient

为方便提取电路的状态空间和输出方程，折线模型等效子电路须满足基尔霍夫电流、电压定律。以图3所示半桥逆变器为例进行分析和说明。

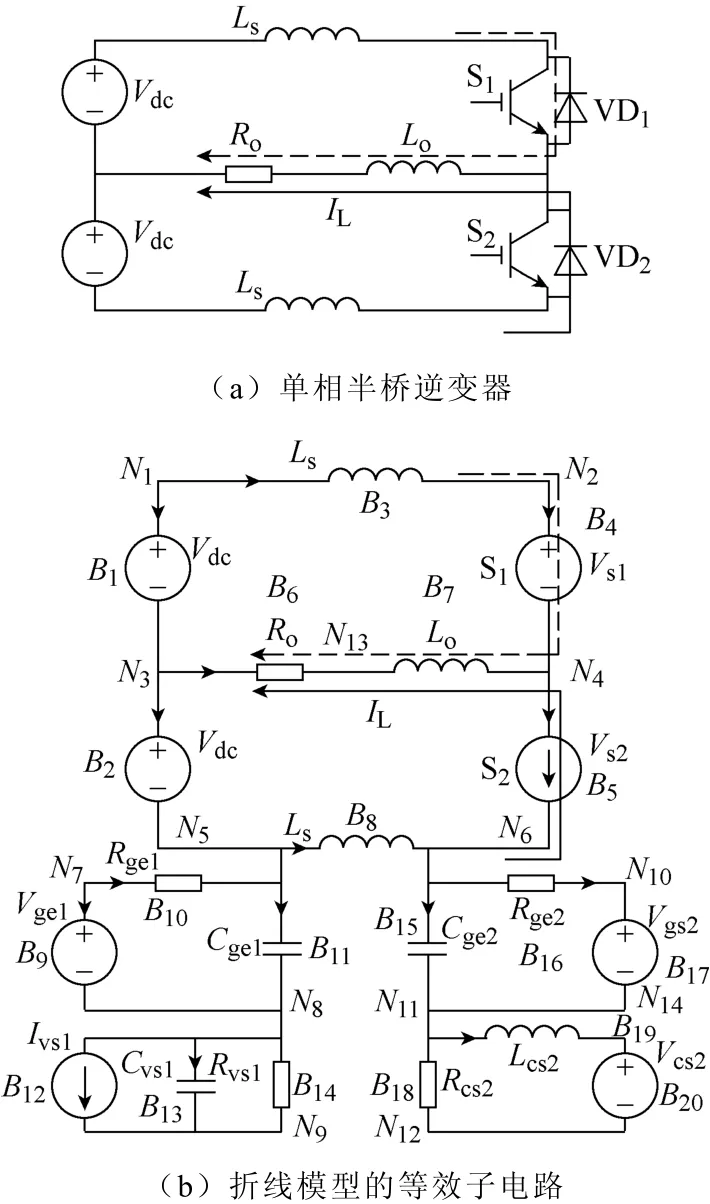
图3 单相逆变电路中器件折线模型的子电路实现Fig.3 Single-phase inverter and its sub-circuit implementation equivalent to the piecewise linear model

图3a中的负载电流IL正由S1换流至VD2。为使上管端电压与图2中 Vce相符，根据替代定理，将S1视作电压源，为使电流与图2中Ic相符，将VD2视作电流源。电压、电流值可由RLC电路给定，如图3b所示。

图3b中的Ni和Bj分别表示节点i和支路j，具体将在2.4节进行介绍与分析。对下半部左上角子电路进行分析，下标1表示与S1相关，电容Cge1端电压表征S1的Vge。在图2中t0～t1时段内，S1的Vge从Vg(on)指数衰减至Vml，于是可选择栅极参数（Vge1、Rge1、Cge1）及Cge1端电压初值，使Cge1端电压等于S1管中的Vge。

2 考虑非理想器件模型电路状态方程提取

本节参考文献[7-10,15,16]，利用电网络分析法，对电路状态方程和输出方程提取方法进行分析与推导。重点是将第1节中的两种模型代入电路，分析并验证该提取方法可得到标准形式状态方程。提出电路的参数结构矩阵的概念，编写提取状态方程的程序，给出程序流程步骤和应用实例。

2.1 电路状态方程的系统提取方法

推导状态方程的关键是确定独立电容电压和电感电流支路。图4给出了电路存在非独立状态变量的典型情况。图4a为只含电压源和电容的回路，显然C1和C2的端电压中只有一个可以作为独立状态变量。同样地，图4b中L1和L2的电流中只有一个可以作为独立状态变量。选取出独立状态变量可以简化状态方程，文献[9,10]选取的方法是在网络中选一棵规范树（normal tree）。规范树的选择依赖于对关联矩阵Qb的操作，将Qb列的顺序从左到右取为电压源、电容、电阻、电感、电流源，通过作初等行变换将Qb变换为阶梯形矩阵，从而可方便地找到所有线性无关的列，这些列对应的支路即构成规范树。可以证明，规范树的树中电容电压和树余中电感电流构成独立状态变量向量，证明见附录。

图4 电路中存在非独立状态变量的典型情况Fig.4 Typical conditions where dependent state variables exist in circuits

电路元件分为八类：树支电压源、电容、电阻、电感、连支电流源、电感、电阻和电容。基尔霍夫电流定律、电压定律以及支路元件端电压-电流关系可以完整描述电路所有电量的关系，即

式中，D、P分别为基本割集矩阵、回路矩阵，矩阵中的列顺序按照上述元件分类顺序排列，附录中对明D、P的表达式进行了说明；i、u分别为各支路电流和电压列向量，元素排列顺序与D、P相同；矩阵I为单位阵；下标T、L分别表示树支和连支；下标E、C、R、L、J分别表示电压源、电容、电阻、电感、电流源；上标T表示矩阵转置；RT、CT、GL、CL、LTT、LTL、LLT、LLL分别为树支电阻、树支电容、连支电导、连支电容、树支间、树支与连支间、连支与树支间、连支间电感值（含自感和互感）的矩阵。

整理式（3）～式（5）可得到状态方程为

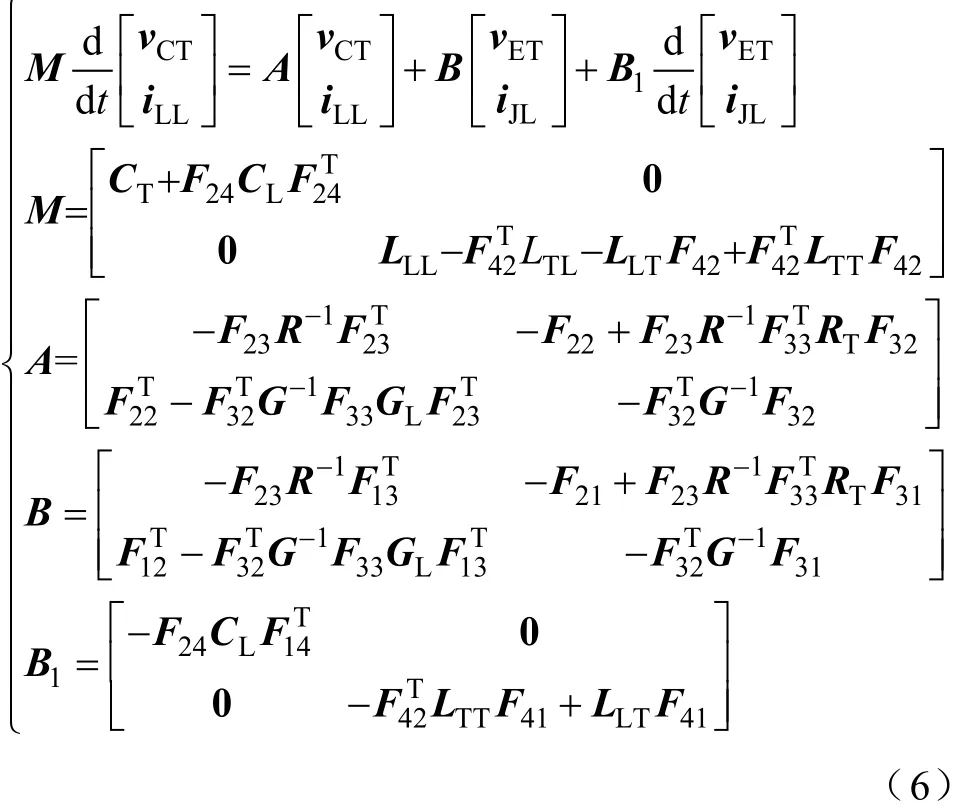
值得注意的是：D中的F34、F43、F44总为零矩阵。例如P中-表示树中电感支路在树余电阻支路形成回路中分布情况，而在规范树的选取过程中导致树余电阻只可能与树中电压源、电容或电阻支路形成回路，所以-总为零矩阵。

2.2 考虑器件行为模型的电路状态方程

本节将把第1节中的两种行为模型代入电路中得到标准形式状态方程。

2.2.1 考虑三端电容模型的状态方程

式（6）所示状态方程存在输入源导数项。在三端电容模型中，Imos作为iJL中的元素处理。当IGBT工作在饱和区时，Imos的导数为

式中，Vge、Vgc均为独立状态变量。

考虑电路只含一个IGBT时，若式（6）中B1为非零矩阵，则式（6）可整理为式中，B1M为B1对应Imos的列；B、iJ′L为将Imos提到等号左侧后B1、IJL中剩下的部分。

对式（8）求解的每一步长中，导数项系数中Vge、Vgc均取上一个步长计算结果，于是在DSED每一个计算步长中，对式（8）整理得状态方程

然后，对式（9）中的矩阵′M求逆。当电路具有一定规模，比如对于一个三相半桥逆变电路，考虑IGBT三端电容模型、母线杂散电感和三相输出电感等参数，方阵M′阶数约为22。若每个计算步长都需要对M′进行求逆，则求解效率会受到很大影响。当电路规模更加大时，M′阶数更高，对M′求逆会导致求解程序的效率更低。

可以证明矩阵B1是零矩阵。对电路建模，需考虑母线电容的等效串联电阻（Equivalent Series Resistance, ESR），于是采用三端电容模型时，电路总不存在只含电压源和电容的回路，各电压源和电容都属于规范树。P中-FiT4（i=1, 2, 3, 4）表示各树支路在树余电容形成回路中的分布，均为空阵。所以矩阵B1左上角的子阵是空阵。-F4T1表示树支电感支路在电流源连支形成回路中的分布，连支电流源指Imos。由于每个连支与树支只形成一个回路，而Imos已与Cge、Cgc两树支形成回路，所以-F4T1是零矩阵。从而可知，B1是零矩阵，式（6）是标准形式的状态方程，当式（6）写成式（1）的形式时，系数矩阵为AS、BS。

2.2.2 考虑折线模型的状态方程

考虑折线模型时，同样也不存在只含电压源和电容的回路，B1左上角子阵应当是空阵。-F4T1表示树支电感支路在电流源连支形成回路中的分布，以图3为例，电流源IVS1已与CVS1树支形成回路，所以-是零矩阵。从而可知，B1是零矩阵，式（6）是标准形式的状态方程。

值得注意的是：以图3为例，将上、下管分别当作电压、电流源，则Vs1、Is2出现在式（6）输入向量中，同时也是状态变量。每一步计算时，先计算Vs1、Is2等状态量，再将其代入剩下的状态方程进行计算。

2.3 电路输出方程的系统提取方法

提取电路输出方程具有重要意义，一方面可以了解所有支路的电量情况，同时也是仿真解算的必要条件。例如，图5为二极管的一种等效电路模型，当用其对实际二极管建模时，就需知道二极管所在支路的电压电流值，以判断功率二极管所处开关状态。

图5 二极管的一种等效电路模型Fig.5 One type of equivalent circuit model for diode

输出方程按元件分类，每一类按树支电流、电压和连支电流、电压的顺序组织，可得式（10）。

附录给出了电容支路输出方程系数矩阵。与前述分析类似，用本文两种器件模型时，可证明输入源导数项系数B1C、B1L、B1EJ均为零矩阵，输出方程总是状态变量与输入量的线性组合。

2.4 系统提取状态方程的程序与应用

本节将定义电路参数结构矩阵，给出提取含器件非理想模型电路状态方程和输出方程的程序步骤，并给出考虑三端电容模型的Buck电路和考虑折线模型的逆变电路这两个算例。

2.4.1 参数结构矩阵及步骤

根据2.1～2.3节，为获得电路状态和输出方程，须知道电路结构（Fij（i=1, 2, 3, 4；j=1, 2, 3, 4）子矩阵）和各支路元件信息。电路参数结构矩阵S某一行向量为

式中，c1～c6为用于示意的某一行6列数。这6列的定义如下：c1为该行对应的支路编号，按1, 2, 3…依次递增；c2为c1支路出点编号；c3为c1支路入点编号；c4为c1支路元件类型，0表示独立电压源，1表示独立电流源，2表示电容，3表示电阻，4表示电感，5表示互感；c5为c1支路的元件参数值；c6为与c1支路电感存在互感的一个电感支路编号。

需将电路当有向图处理，先给电路的每个节点、支路各按1、2、3连续编号，为各支路规定参考方向，按照编号和参考方向得到S。提取状态方程和输出方程系数矩阵的程序以矩阵S为输入，程序步骤见附录。

2.4.2 算例1（Buck电路）

图6为Buck电路，其中Ni、Bj分别表示节点i和支路j。N2与N4之间是图5的二极管等效电路，Ls为杂散电感，LO、RO为阻感性负载。采用IGBT的三端电容模型，本例仅为示意，除了断态理想二极管等效电阻RDM取为1MΩ，图6中其他电阻、电容、电感均分别取值为1Ω、1F、1H。

获取图6中的矩阵S后，将S代入程序，即可得到式（6）写成式（1）形式后的系数矩阵，即

图6 对Buck电路的编号Fig.6 Numbering for Buck circuit

式中，状态变量按5、8、11、14支路电容电压和2、7支路电感电流排列。可验证式（12）的正确性。此处未给出输出方程的系数矩阵。式（6）中对源求导的系数矩阵B1计算为零矩阵，与理论分析一致，此处也未给出。

2.4.3 算例2（全桥逆变电路）

将图3b的状态方程写成式（1）形式后的系数矩阵为

式中，状态变量按11、13、15支路电容电压和7、19支路电感电流排列。为了示意，所有元件参数值均取为1。此处未给出输出方程的系数矩阵，且式（6）中对源求导的系数矩阵B1在这里计算也为零矩阵，同样未给出。

2.4.4 算法的优缺点分析

该状态方程提取与分析法，可较方便地获得状态方程和输出方程系数矩阵，但仍然存在两个问题：①前文提及的对矩阵M求逆；②系统刚性。

关于对矩阵M求逆，观察式（6）可知，只有电容值改变才会引起M变化，而只有电阻（三端电容模型中的Rge、Rce和折线模型中子电路的电阻）改变时，程序可以使用上一步长M的逆。从这个角度出发，实现折线模型各阶段形状时，需尽量保持图3b中Cge1、Cvs1、Cge2、Lcs2不变，而只是改变Rge1、Rvs1、Rge2、Rcs2。

采用这两种模型时，各电压源和电容都在规范树中，所以连支电容矩阵CL为零矩阵。矩阵M左上角的子矩阵是一个对角矩阵，右下角子矩阵是一个对称矩阵，所以对M求逆可以使用一些优化算法。与文献[11]的算法比较，为获得标准形式状态方程，后者也需要对一个对称矩阵K1求逆，如

因为K1右下角是单位子阵，KC是一个对称矩阵。所以K1维数是电路节点数的2倍，M的维数是状态变量数。可见，为得到标准形式的状态方程，不可避免地需对这种类型的矩阵求逆。

至于系统刚性问题，当电路中元件参数值相差较大时，状态方程的刚性问题就会产生。比如，建模时将二极管视作二值电阻，各二极管开通关断时的阻值相差巨大，这会加剧系统刚性，该问题可在数值算法方面尝试克服，本专题其他文献针对此问题提出了更为适用系统刚性的后向DSED[17]和线性隐式DSED等方法，本文不再赘述。

3 DSED方法电路解算算例

本节结合DSED方法获得仿真计算波形，用以说明所提方法的有效性及优势。

仿真对象是如图7所示的三相两电平逆变器，用本文提出的状态和输出方程提取方法，列写电路参数结构矩阵S。此时式（1）中的系数矩阵AS、BS维数分别为17×17、17×7。此处只说明其中的状态变量按3、6、8、10、14、17、19、21、26、29、32、34支路电容电压和2、24、36、40、41支路电感电流排列。

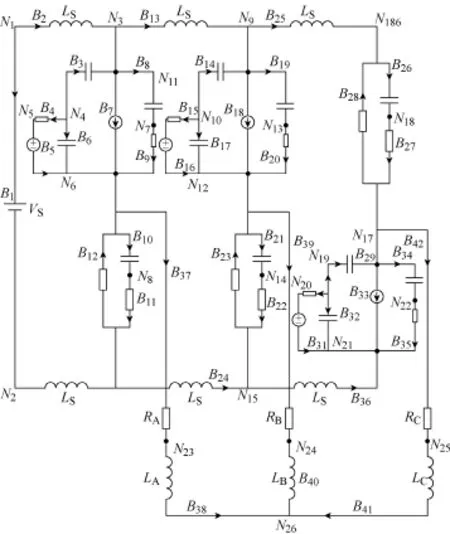
图7 三相两电平逆变器仿真模型Fig.7 Simulation models for three-phase two-level circuit

在提取状态方程和输出方程的基础上，运用DSED中的ODE算法得到了三相两电平逆变电路一个开关周期的仿真波形，如图8所示。其中，图8a为未采用DSED方法求解的电压、电流波形，图8b为采用了适用于系统刚性的ode23tb算法。各算法在三相两电平电路单开关周期仿真中的性能比较见表1。可见，该状态方程提取方法与DSED数值算法结合后，大大提高了电力电子电路求解的有效性和快速性。值得一提的是，表1中的仿真总耗时将状态方程提取和数值算法计算的耗时都计入在内，而前者耗时不到0.01s，对总耗时的影响很小。

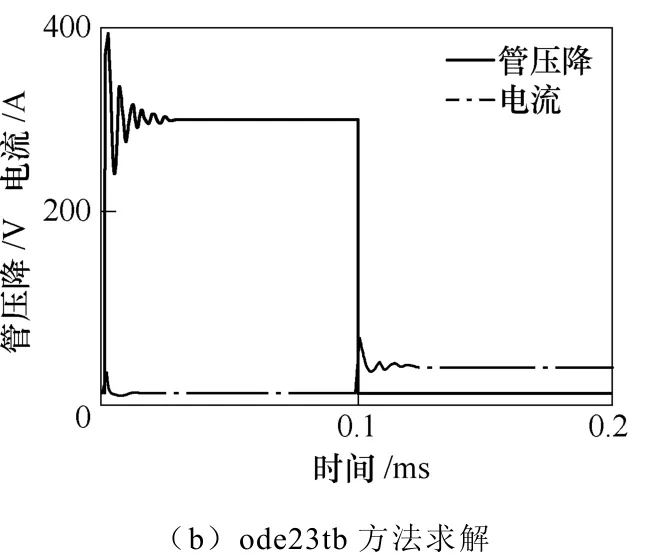
图8 三相两电平逆变电路的两种算法仿真波形Fig.8 Simulation waveforms with two algorithms for three-phase two-level circuit

表1 各算法在三相两电平电路单开关周期仿真中的性能比较Tab.1 Simulation comparison of various algorithms for three-phase two-level converter in one switching period

4 结论

1）本文介绍了IGBT的两种行为模型，并针对折线模型提出了其对应的等效子电路实现方法。提出了用网络图论提取状态方程的方法，推导输出方程的表达式，给出提取状态方程和输出方程的程序步骤。证明了将IGBT两种行为模型代入电路均可以得到标准形式的状态方程，且输出方程也是输入源和状态变量的线性组合。采用Buck和全桥逆变电路，验证了当考虑两种行为模型时，提取状态和输出方程程序的正确性。

2）本文分析了状态方程分析法存在的两个问题：需要频繁对一定规模矩阵求逆，对含器件数目较大的电路仿真计算的效率，是很大的挑战；系统刚性问题，并给出了部分解决方法和思路。进一步将基于图论的电路方程提取方法与DSED中ODE算法结合，用于计算电力电子电路。但是第3节中的算例只是对一个开关周期进行了仿真，所以提取状态方程的耗时很小。而对更大规模电路进行更长时间仿真时，状态方程提取的耗时可能对仿真速度产生一定影响，还需进一步研究、优化。

附 录

1. 关于树中电容电压和树余中电感电流构成独立状态变量的证明

规范树的选取基于网络分析中一个基本结论：一个n节点有向图的关联矩阵Qb中n-1列对应支路构成一棵树的充要条件是Qb中这n-1列线性无关。分析分两部分进行：

（1）先分析电容支路。由2.1节规范树的选取过程及选取前Qb列的顺序可知：①树中电压源和电容不构成回路，所以树中各电容电压相互独立；②树余中各电容支路都与树中电压源或电容构成回路，因此它们都可用树中电压源和电容支路电压线性表示。

（2）再分析电感支路。①任一树支电感电流iL可唯一确定一个割集CS。CS中除iL外其他连支如果含电容或电阻，则这些连支电容、电阻就会与iL及其他一些支路构成回路。但是由2.1节规范树的选取过程可知，连支电容、电阻都只能与树中非电感支路形成回路。因此，任一树支电感电流iL只能与树余中电感或电流源构成割集，即任意树支电感电流都可用树余中电感或电流源电流线性表示。②不存在只含树余中电感或电流源的割集，否则规范树的所有支路将必须位于该割集划出两子图中的一个子图Gsub，而树的定义决定了Gsub已经包含网络所有节点，这显然是矛盾的。

根据上述两部分分析可知：树余中电容电压可由树中电压源和电容电压线性表示，树中电感电流可由树余中电流源和电感电流线性表示，树中电容电压和树余中电感电流构成了完备的独立状态变量。

2. 获得电路状态方程和输出方程系数矩阵的程序步骤

（1）将原电路中IGBT用三端电容或折线模型等效子电路替换。按照2.4.1节的方式，对所有节点、支路进行编号，对所有支路规定参考方向，列出参数结构矩阵S 。

（2）根据S中第四列元素类型，提取电路的关联矩阵Qb，Qb的列从左向右依次对应电压源、电容、电阻、电感、电流源。根据2.1节的方法选规范树，并将Qb中列的顺序重新整理得到Q，Q的列从左向右依次对应规范树电压源、电容、电阻、电感和连支电流源、电感、电阻、电容。

（3）根据列分属于树支、连支，将第2节中基本割集矩阵D和基本回路矩阵P、Q分别写成如下分块形式。

根据第2节中对D、P的定义，根据Q求解出D、P。DT为阶数等于树支数的单位矩阵；PL为阶数等于连支数的单位矩阵。

至此，得到了系数矩阵中所有的Fij（i,j=1, 2, 3, 4）矩阵。

（4）根据步骤（2）和（3）的结果，再获取参数矩阵CT、CL、LTT、LTL、LLT、LLL、RT、CL。

（5）将结构矩阵和参数矩阵代入状态方程和输出方程的系数矩阵表达式。

3. 关于电容支路输出方程中系数矩阵的表达式

先将式（6）整理为

其中

式中，系数矩阵M-1A的行和列均按树支电容支路数和连支电感支路数来划分子块；系数矩阵M-1B、M-1B1的行均按树支电容支路数和支路电感支路数来划分，列均按照电压源数和电流源数来划分子块。

将式（10）中关于电容支路输出方程的系数矩阵都划分为4×2的分块矩阵，即

这些分块矩阵的维数都可由式（10）和式（A5）对照获得。划分的分块矩阵都可用式（A4）中M-1A、M-1B、M-1B分块子矩阵来表示，即1

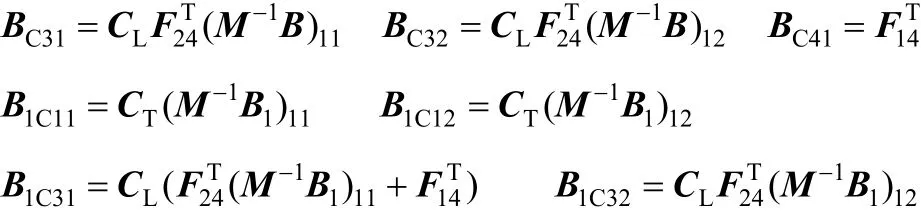
式中，AC21为单位矩阵；AC22、BC21、BC22、B1C21、B1C22、AC42、BC42、B1C41、B1C42为零矩阵。

[1] Cellier F E, Kofman E. Continuous system simulation[M]. New York： Springer Science and Business Media, 2006.

[2] Kofman E, Junco So. Quantized-state systems： a DEVS approach for continuous system simulation[J]. Transactions of the Society for Modeling and Simulation International, 2001, 18(3)： 123-132.

[3] Migoni G, Kofman E. Linearly implicit discrete event methods for stiff ODE’s[J]. Latin American Applied Research, 2009, 39(3)： 245-254.

[4] Cellier F E, Kofman E, Migoni G. Quantized state system simulation[C]//Grand Challenges in Modeling and Simulation, 2008： 504-510.

[5] Migoni G, Bortolotto M, Kofman E. Linearly implicit quantization-based integration methods for stiff ordinary differential equations[J]. Simulation Modelling Practice and Theory, 2013, 35(6)： 118-136.

[6] Migoni G, Kofman E. Quantizati-on-based simulation of switched mode power supplies[J]. Transactions of the Society for Modelling and Simulation International, 2015, 91(4)： 320-336.

[7] Wasynczuk O, Sudhoff S D. Automated state model generation algorithm for power circuits and systems[J]. IEEE Transactions on Power Systems, 1996, 11(4)：1951-1956.

[8] Allmeling J H, Hammer W P. PLECS-piece-wise linear electrical circuit simulation for simulation[C]// IEEE International Conference on Power Electronics and Drive Systems, 1999： 355-360.

[9] 张科. 建立多元有理函数域上RLC电网络状态方程的软件设计[D]. 武汉： 武汉理工大学, 2004.

[10] Chua Leon O, Lin Pen-Min. Computer-aided analysis of electronic circuits： algorithm and computational techniques[M]. Englewood Cliffs, N. J.： Prentice-Hall, 1975.

[11] 纪峰, 魏晓光, 吴学光. 线性开关电路电磁暂态分析的状态方程法[J]. 中国电机工程学报, 2016, 36(22)： 6028-6037. Gi Feng, Wei Xiaoguang, Wu Xueguang. State space method to analyze the electromagnetic transient of linear switching circuit[J]. Proceedings of the CSEE, 2016, 36(22)： 6028-6037.

[12] Sheng Kuang, Williams B W. A review of IGBT models[J]. IEEE Transactions on Power Electronics, 2000, 15(6)： 1250-1266.

[13] Kang Wangying, Ahn H. A parameter extraction algorithm for an IGBT behavioral model[J]. IEEE Transactions on Power Electronics, 2004, 19(6)：1365-1371.

[14] Ji Shiqi, Lu Ting, Zhao Zhengming, et al. Modelling of high voltage IGBT with easy parameter extraction[C]// IEEE 7th International Power Electronics and Motion Control Conference-ECCE Asia, 2012： 1511-1515.

[15] Foulds L R. Graph theory applications[M]. New York：Springer-Verlag, 1992.

[16] Bondy J A, Murty U S R. Graph theory[M]. New York： Springer, 2008.

[17] 李帛洋, 赵争鸣, 檀添, 等.后向离散状态事件驱动电力电子仿真方法[J]. 电工技术学报, 2017, 32(12)：42-49. Li Boyang, Zhao Zhengming, Tan Tian, et al. A backword discrete state event driven simulation method for power electronics based on finite state machine[J]. Transactions of Electrotechnical Society, 2017, 32(12)： 42-49.

（编辑 张玉荣）

State Space Method to Analyze the Power Electronics Circuits Considering Devices’ Non-Ideal Models

Ling Yatao Zhao Zhengming Yang Yi Li Boyang Yuan Liqiang
（State Key Laboratory of Control and Simulation of Power Systems and Generation Equipments Deptartment of Electrical Engineering Tsinghua University Beijing 100084 China）

At present, there are some problems in the simulation software of power electronics, such as rough simulation waveforms for device switching transients, non-convergence for stiff systems etc. Hence, our group has proposed an analysis method—discrete state event drive (DSED) based on quantized state system (QSS). In this method, the algorithm based on circuit topology and state is integrated that can identify the switching states of devices and extract state space equations. Thus, a graph-theory-based algorithm that can extract the state and output equations is proposed. It is proved theoretically that the state space equations of power electronic systems are always in norm-form. Furthermore, parameter-structure matrix is proposed. Some discussions are carried out to the problem that every time a switch alters its status, the coefficient matrices of state space equations must be recalculated. Finally, simulation results of classical circuits have verified the proposed method.

State space analysis method, device non-ideal characteristics, device models, discrete state event drive (DSED), simulation performance

TM46

凌亚涛 男，1992年生，博士研究生，研究方向为电力电子仿真算法。

E-mail： 1546517440@qq.com（通信作者）

赵争鸣 男，1959年生，教授，博士生导师，主要研究方向为大容量电力电子变换系统、光伏发电、电机控制、无线电能传输等。E-mail： zhaozm@tsinghua.edu.cn

10.19595/j.cnki.1000-6753.tces.170446

国家自然科学基金重大项目资助（51490680，51490683）。

2017-04-18 改稿日期 2017-05-15