砂土微宏观性质相依关系研究

易长圭

(湘潭大学 土木工程与力学学院, 湖南 湘潭, 411105)

砂土微宏观性质相依关系研究

易长圭

(湘潭大学 土木工程与力学学院, 湖南 湘潭, 411105)

为了研究砂土微观力学性质, 采用了离散单元法对砂土进行三轴试验模拟, 并引入抗转动模型来表征砂土颗粒的抗转动效应。通过对选取的不同法向接触刚度、刚度比、颗粒内摩擦角、滚动刚度系数以及塑性弯矩系数进行三轴排水数值试验, 得到了砂土不同微观参数与其宏观力学性质的对应关系。试验结果表明:法向接触刚度对砂土弹性模量影响显著, 并呈现正相关线性关系; 刚度比与砂土泊松比呈现较为显著的负相关线性关系; 颗粒内摩擦角对砂土宏观内摩擦角影响显著, 滚动刚度系数影响砂土残余强度, 塑性弯矩系数主要影响峰值强度。

离散单元法; 砂土; 微观参数; 宏观参数

离散单元法是上个世纪70年代由Cundall[1]提出的一种基于非连续介质力学的数值计算方法。其基本思想是把所研究材料离散为单个单元, 各个单元运动由牛顿第二运动定律控制。由于离散单元法在颗粒尺度上对物理量变化进行考量, 因此, 其得到了广泛应用。在岩土工程领域内, 离散单元法已经成功应用于砂土剪切[2]、结构性土压缩试验[3]、非饱和土吸力[4]等研究中。离散单元法计算原理虽然简单, 但由于接触模型参数属于颗粒尺度参数, 这些细观参数通常是未知的, 又无法通过试验直接获取, 所以选取一个合理的计算参数十分困难, 而在进行离散单元法模拟时, 只有细观计算参数正确的前提下, 才能获得一个合理的计算结果[5]。目前, 离散元微观参数的选取方式多种多样, 目前大多数研究者采用试错法[6]。针对微观参数选取的研究主要集中在细观颗粒力学分析以及宏观试验推导两个方面。武力等[7]将遗传神经网络与三轴试验离散元数值模拟结合起来, 并进行改性砂土颗粒离散元接触模型参数反演;邢纪波等[8]根据应力传播条件给出了颗粒间接触刚度的理论计算公式, 并给出了求解静态问题的自适应阻尼; 王泳嘉等[9]依据两弹性球受集中力作用情况, 得到了法向和切向刚度的理论公式; 此外,Mindlin[10]、Hentz[11]、张振南等[12]也通过相关研究得到了接触刚度表达式; 徐小敏[13]等通过室内三轴试验进行回归分析得到了宏微观参数之间的经验公式; 焦红光等[14]通过离散元模拟指出接触刚度与计算时步存在较大的关联; Alessio等[15]提出了岩土材料宏微观结合的微观本构模型, 并采用该模型对凝灰岩的本构模型参数进行了预测。

综上所述, 目前针对离散元微观参数和其宏观力学特征直接相依关系的研究较为少见, 本文运用大型离散元程序SDEC进行了大量的三轴试验模拟, 并将适用于模拟砂土力学性质的抗转动模型引入进程序中。针对模型中关键微观参数进行分析, 研究了刚度比、法向接触刚度、颗粒间摩擦角、滚动刚度系数以及塑性弯矩系数对砂土宏观力学性能的影响, 并详细分析了各个微观参数在宏观上所对应的力学响应, 得到了各个微观参数与砂土宏观参数的相依规律。

1 DEM抗转动模型

颗粒的不规则形状是影响砂土力学性能的主要因素。为充分表征砂土的力学性能, 在线性接触模型的基础上, 将Blheine所提出的抗转动模型引入进该数值计算中。如图1所示, 颗粒之间的相互作用受到法向接触、切向接触以及转动接触三个部分共同作用。

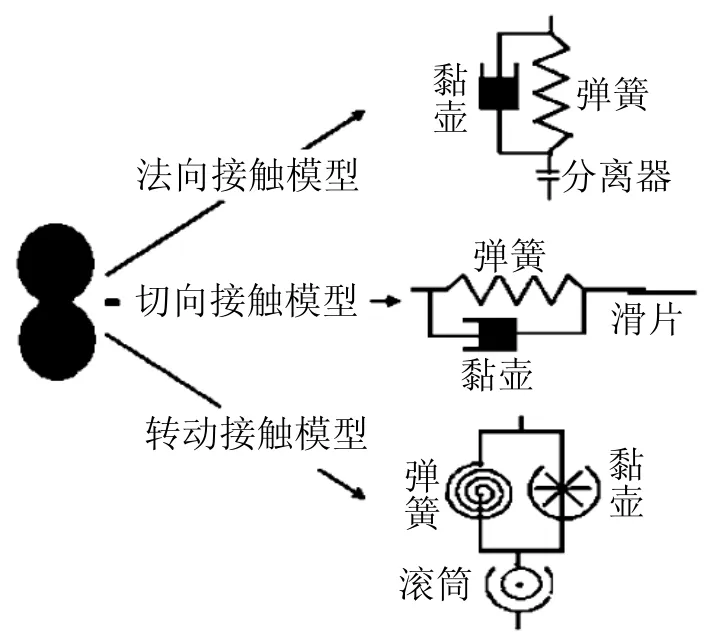
图1 颗粒抗转动接触模型

颗粒间法向接触力Fn和切向接触力Ft分别由2个方向上的颗粒相对位移及接触刚度控制, 计算公式分别为Fn= KnUn和ΔFt= KsdUs。式中: Un为法向位移; dUs为切向位移增量; Kn和Ks分别为颗粒间法向接触刚度和切向接触刚度。当颗粒间接触力Fn和Ft满足关系Ft≥ Fntanμ时, 颗粒之间不产生滑动, μ为颗粒间摩擦角。

图2给出了接触模型不同部分的力学响应关系。从图2(c)可以看出, 转动弯矩逐渐从零增长到最大值, 其值与相对转动角呈现出一定的关系, 具体计算式为ΔMr= krΔθr。式中, kr= βKsr2为颗粒滚动刚度,其中β则表示无量纲滚动刚度系数, r表示接触颗粒的平均半径, Δθr为两接触颗粒间单位时间内的相对转动角。颗粒间最大转动弯矩可由方程Mp= ηr|Fn|计算, 式中, η为无量纲塑性弯矩系数。

图2 接触模型力学特征

2 模型验证

为验证该离散元模型正确性, 采用抗转动模型对Labenne砂土进行三轴试验模拟, 并与相关文献的试验数据进行对比分析。Labenne砂土物理性质如表1所示。

三轴试验采用开源离散元程序SDEC进行模拟, 试样为50 mm × 50 mm × 50 mm立方体, 试样由8 120个颗粒组成(图3(a)), 边界为六面刚性墙体, 在固结过程中, 六面刚性墙体往试样中心移动直到达到指定围压。剪切过程中, 周边墙体通过伺服控制其应力不变, 以达到稳定围压的状态, 而上下墙体同时以一定速率向中心移动进行剪切。为充分模拟Labenne砂土性质, 首先在100 kPa围压下对接触模型微观参数进行标定, 得到合理微观参数如表2所示。然后采用所标定参数, 进行200 kPa围压下三轴试验模拟, 并与室内试验数据进行对比, 结果如图3(b)、3(c)所示。

表1 Labenne砂土物理性质

表2 接触模型参数

由图3(b)可知, 在不同围压下, 数值试验应力—应变曲线和室内试验曲线吻合良好, 所采用抗转动模型能较为准确地描述砂土应力—应变的非线性关系。从图3(c)可知, 在固结排水状态三轴试验中, 采用抗转动模型可反映试样剪切过程中的先剪缩后剪胀现象, 能准确描述剪切过程中试样体积变化。

图3 模型试验及试验结果对比

3 三轴试验设计

为研究砂土中微观力学性能对其宏观力学性质的影响, 采用离散单元法进行不同微观参数下的三轴试验模拟。模拟所采用围压均为200 kPa, 颗粒密度为2650 kg/m3, 时步长为10-7s。所选取微观参数分别为法向接触刚度、刚度比、颗粒内摩擦角、塑性弯矩系数和滚动刚度系数。具体实施方案如表3所示。

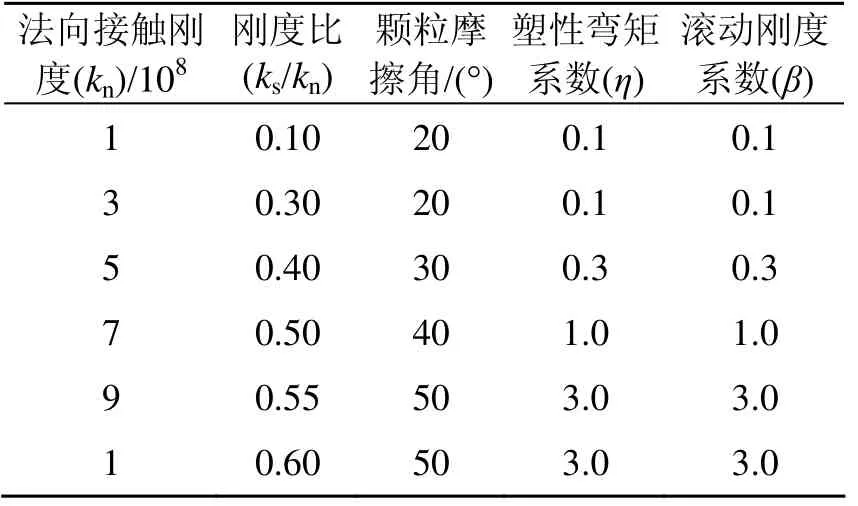
表3 三轴数值试验方案

4 结果与分析

4.1 微观弹性参数

图4 微观弹性参数宏观响应

维持其他微观参数不变的情况下, 分别改变刚度比和法向接触刚度进行三轴剪切试验, 得到了刚度比与泊松比以及法向接触刚度与弹性模量之间的关系, 结果如图4所示。

由图4(a)可知, 随着刚度比从0.1增长至0.6, 砂土泊松比从0.23下降至0.13, 刚度比与砂土泊松比呈现出明显的负相关线性关系。此外, 从图4(b)可知, 随着法向接触刚度从1 × 108增长到1 × 109N/m,试样弹性模量从156 kPa增长至907 kPa, 且颗粒间法向接触刚度和试样弹性模量呈现出良好的正相关线性关系。

4.2 不同微观强度参数下应力—应变关系

通过整理试验过程中不同颗粒内摩擦角、不同滚动刚度系数以及不同塑性弯矩系数下的试样强度变化曲线, 得到相关偏应力—应变关系如图5所示。从图5可以看出, 颗粒间内摩擦角以及2个抗转动系数均对峰值强度有一定影响, 而仅滚动刚度系数对试样残余强度产生影响。

由图5(a)可知, 随着颗粒间摩擦系数的增大, 峰值应力逐渐增大, 但颗粒间摩擦角增长至40°后, 随着摩擦角增大,峰值应力上升趋势逐渐减慢。由图5(b)可知, 随着滚动刚度系数增大, 峰值强度和残余强度均呈现增大趋势, 但当滚动刚度系数大于1.0时, 峰值强度以及残余强度几乎不再变化。由图5(c)可知, 塑性弯矩系数从0.1增长至0.3时, 峰值强度从394 kPa增长至480 kPa, 而随着塑性弯矩系数继续增大至1.0后, 峰值强度不再产生变化。

图5 应力应变关系曲线

4.3 不同微观强度参数下的体变

通过整理试验过程中不同颗粒内摩擦角、不同滚动刚度系数以及不同塑性弯矩系数下的试样体积变化曲线, 得到如图6所示结果。

由图6(a)可知, 颗粒间摩擦角对体积变化影响显著, 尤其体现在后期剪胀阶段。摩擦角从20°增至40°时, 试样最大体变值从7.1%增至9.4%。而颗粒间摩擦角继续增长至50°时, 体变值仅增加了0.6%。

图6 体变关系曲线

从图6(b)可以看出, 滚动刚度系数对体积变化的影响较小, 仅在后期剪胀阶段存在一定影响。随着滚动刚度系数从0.1增长至1.0, 最大体变量从9.7%增长至10.7%, 但当滚动刚度系数继续增加至3.0时, 最大体变量几乎不再变化。由图6(c)可知, 塑性弯矩系数几乎不对试样的体变产生影响。

5 结论

通过采用离散单元法对砂土性质进行表征, 并采用室内试验与数值试验相结合的方法对所建立模型进行验证, 建立了符合砂土力学性质的离散元模型。通过一系列三轴排水试验模拟, 确定模型中微观参数与砂土宏观力学性质之间的对应关系, 得到如下主要结论: (1) 抗转动模型能较好地描述砂土非线性应力—应变关系以及剪缩、剪胀等体积变化特征。(2) 刚度比对泊松比呈现较为明显地影响, 并随着刚度比的增大, 泊松比逐渐降低,两者呈现明显线性关系。(3) 法向接触刚度对弹性模量影响较大, 随着法向接触刚度增大, 弹性模量逐渐增大, 且两者呈现较好的线性关系。(4) 颗粒内摩擦角对颗粒宏观摩擦角影响较大; 滚动刚度系数对残余强度有较为明显地影响; 塑性弯矩系数主要影响试件应力峰值强度。

[1] Cundall P A. A Computer model for simulating progressive large scale movements in blocky rock system [C]// Proceedings of the Symposium of the International Society of Rock Mechanics. Nancy, France, 1971: 11-19.

[2] Thornton C. Numerical simulations of deviatoric shear deformation of granular media [J]. Geotechnique, 2003, 50(1):43-53.

[3] Jiang Ming-jing, Yu H S, Harris D. Bond rolling resistance and its effect on yielding of bonded granulates by DEM analyses [J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2016, 30(7): 723-761.

[4] Liu S H, Sun D A. Simulating the collapse of unsaturated soil by DEM [J]. Int J Numer Anal Meth Geomech, 2012, 26:633–46.

[5] 周健, 贾敏才. 土工细观模型试验与数值模拟[M]. 北京: 科学出版社, 2008.

[6] Manuel J M M, Luis E M R. Discrete numerical model for analysis of earth pressure balance tunnel excavation [J]. Journal of geotechnical and geoenvironmental engineering, 2015, 131(10): 1 234–1 242.

[7] 武力, 屈福政, 李守巨. 土压平衡盾构改性砂土离散元模型参数反演方法研究[J]. 大连理工大学学报, 2013, 50(6):860–866.

[8] 邢纪波, 俞良群, 张瑞丰, 等. 离散单元法的计算参数和求解方法选择[J]. 计算力学学报, 1999, 16(1): 47–51, 99.

[9] 王泳嘉, 邢纪波. 离散单元法及其在岩土力学中的作用[M]. 沈阳: 东北工学院出版社, 1991.

[10] Mindlin R D. Compliance of elastic bodies in contact [J]. Journal of Applied Mechanics, 1949, 71(3): 258–269.

[11] Hentz S, Daudevile L, Donze F V. Identification and validation of a discrete element model for concrete [J]. Journal of Engineering Mechanics, 2012, 130(6): 709–719.

[12] 张振南, 葛修润, 李永和. 基于虚内键理论的材料多尺度力学模型[J]. 固体力学学报, 2006, 27(4): 325–329.

[13] 徐小敏, 凌道盛, 陈云敏, 等. 基于线性接触模型的颗粒材料细–宏观弹性常数相关关系研究[J]. 岩土工程学报,2010, 32(7): 991–998.

[14] 焦红光, 李靖如, 赵继芬, 等. 关于离散元法计算参数的探讨[J]. 河南理工大学学报(自然科学版), 2007, 26(1):88–93.

[15] Alession N, Bernhard S, Marek L. Application of artificial neural network for identification of parameters of a constitutive law for soils [J]. Lecture Notes in Artificial Intelligence, 2013, 2 718(2): 545–554.

(责任编校: 江河)

Research on relationships between microscopic and macroscopic properties of sand

Yi Changgui
(College of Civil Engineering and Mechanics, Xiangtan University, Xiangtan 411105, China)

To investigate the microscopic mechanical properties of sand, a series of consolidated drained triaxial test is performed via discrete element method. In addition, the rolling resistance contact model is added into simulations.Five different microscopic parameters are discussed, namely, the normal contact stiffness, the stiffness ratio, the internal friction angle, the coefficient of rolling stiffness, as well as the coefficient of plastic moment. Finally, the relationship between microscopic parameters and macroscopic properties of sand is obtained. The results show that the normal contact stiffness shows a positive linear correlation with the Young’s Modulus, and the stiffness ratio shows a negative linear correlation with the Possion’s ratio, and the internal friction angle has a significant influence on friction angle; the coefficient of rolling resistance is chosen to control the residual strength; the coefficient of plastic moment play a major role in peak stress.

discrete element method; sand; microscopic parameters; macroscopic parameters

TU 433

: A

1672–6146(2017)03–0064–05

10.3969/j.issn.1672–6146.2017.03.014

易长圭, yichangguixtu@163.com。

: 2017–04–13