不确定随机神经网络的几乎必然指数稳定

张景发

(华南理工大学 数学学院, 广东 广州, 510640)

不确定随机神经网络的几乎必然指数稳定

张景发

(华南理工大学 数学学院, 广东 广州, 510640)

为了探讨带有时变时滞的不确定随机神经网络的几乎必然指数稳定问题, 通过构造一个合适的李雅普诺夫函数, 利用李雅普诺夫函数法、随机分析法及线性矩阵不等式得到了不确定随机神经网络的几乎必然指数稳定的充分条件, 验证了已知条件满足引理, 表明带时滞的随机系统在时滞小于某个上界时，带时变时滞的不确定随机神经网络是几乎必然指数稳定的。所给出的判据是由线性矩阵不等式表示的, 该判据是否有解可以通过Matlab工具箱快速地得到解决。

随机神经网络; 几乎必然指数稳定; 李雅普诺夫函数; 线性矩阵不等式; 时滞

过去几十年以来, 神经网络这一领域不断地被发展、研究, 获得了大量的研究成果, 并广泛地运用于组合优化、信号过程、模式识别等领域[1–3]。这些领域的运用都紧紧地依赖于神经网络的动力学行为,其中稳定性是神经网络动力学行为中最重要的性质[4–11]。由于系统建模、测量误差、系统线性化等原因,神经网络常常受到参数不确定和随机干扰因素的影响, 导致系统动力学行为不理想或系统性能差。文献[12–19]研究了参数不确定因素或者随机干扰因素。另外, Deng等[20]研究了带有马尔科夫链的随机微分方程的几乎必然指数稳定性, Guo等[21]研究了一类时滞系统的几乎必然指数稳定。上述文献只是研究了不确定随机神经网络的鲁棒稳定性及渐近稳定等问题, 但是对于带有不确定性和时滞的随机神经网络的几乎必然指数稳定的研究文献比较少。本文研究一类带有区间实变时滞的不确定随机神经网络的几乎必然指数稳定。

1 预备知识

一般地, (Ω, Γ,{Γt}t≥0,ρ)表示全概率空间, 滤子流{Γt}t≥0包含所有的零测子集且右连续。ω(t)=[ω1(t),ω2(t),…,ωm(t )]为定义在全概率空间上的m维布朗运动。Rn表示n维欧几里德空间,表示欧几里德空间的范数。Rn×n表示n×n维的实矩阵集合, In为nn维单位矩阵。对于对称矩阵A∈Rn×n,λmax(A)、λmin(A)分别表示矩阵A的最大特征值及最小特征值。AT表示矩阵A的转置。对于对称正定矩阵X和Y, X-Y＞0表示对称正定的。对称矩阵中符号*表示对称位置的元素的转置, diag{M1, M2,…,Mn}表示对角矩阵的简写。考虑一般的随机微分方程

这里x(t)∈Rn表示神经元的状态向量, τ1(t)、τ2(t)是2个不同的神经元时变时滞,是m维布朗运动, f(x(t), t)是恰当维的向量函数, g(x(t), t)是恰当维的矩阵函数。为简单起见, 假设f(0)=0和g(0)=0, 因此可知x(t)≡0是方程(1)的平凡解。

假设1 设随机微分方程(1)的f、g是Borel可测, 并且存在2个非负常数K1、K2使得对于任意x、,t≥0,有。

定义1 如果方程(1)的解对于所有的满足, a.s.则随机微分方程(1)的平凡解是几乎必然指数稳定的。设C2,1(Rn×[t0,+∞];R+)表示Rn×[t0,+∞]上关于x两次连续可微, 关于t一次连续可微的所有非负函数V(x(t), t)的全体。对任意的(x,t)∈Rn×[t0,+∞], 则对V(x(t), t)有如下伊藤微分公式:

本文考虑如下形式的不确定随机神经网络

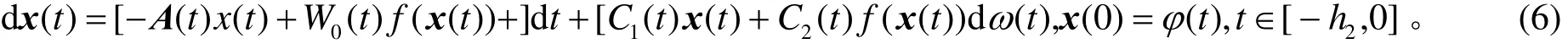
假设2 系统参数不确定矩阵ΔA(t),ΔW0(t),ΔC1(t),ΔC2(t)满足假设3 激活函数f(x(t))每个分量fi(⋅)是连续函数, 存在实数, 使得对于任意的xi∈R 有, 定义对角矩阵

引理1[21]假设存在函数V(x(t), t)∈C2,1(Rn×[t0,∞];R+)和常数p＞0, c1＞0, c2＞0, c3≥0使得对于任意的x≠0, 当t≥t0时,

则随机微分方程(1)的平凡解是几乎必然指数稳定。

引理2[22]对于适当维的矩阵Ψ11, Ψ12,Ψ22, 且满足当且仅当。

引理3[23]对于任意向量x, y∈Rn, 矩阵P∈Rn×n且P＞0, 那么2xTy≤xTP-1x+yTPy成立。

引理4[24]假设M, N, X是适当维的实矩阵, 且矩阵X满足X=XT, 则对于所有F(t)满足FT(t)⋅F(t)≤I, 有X+MF(t )N+NTFT(t )MT＜0,当且仅当存在标量ε＞0使得X+ε-1MMT+εNTN＜0。

引理5[21]假设引理1和假设1成立, 那么存在一个正数τ∗使得对于任意初值, 当τ＜τ∗时随机微分方程(3)的解有该引理表明随机微分方程(1)的平凡解是几乎必然指数稳定时, 随机时滞微分方程(2)的平凡解也是几乎必然指数稳定的。

2 几乎必然指数稳定判据

通过引理2, 本文找到一个合适的李雅普诺夫函数, 并利用LMIs的方式得到如下定理。

定理1 如果存在正定矩阵P, 正定对角矩阵D=diag(d1, d2,…,dn)以及实数α≥0, 使得

3 总结

本文通过构造一个正定的李雅普诺夫函数, 利用李雅普诺夫函数法、随机分析方法及线性矩阵等式得到了不确定随机神经网络的几乎必然指数稳定的充分条件, 然后根据定理得出带时变时滞的不确定随机神经网络的几乎必然指数稳定。

[1] Haykin S. Neural Networks: A Comprehensive Foundation [M]. New Jersey: Prentice Hall, 1998.

[2] Joya G, Atencia M A, Sandoval F. Hopfield neural networks for optimization: study of the different dynamics [J].Neurocomputing, 2002, 43(3): 219–237.

[3] Young S S, Scott P D, Nasrabadi N M. Object recognition using multilayer Hopfield neural network [J]. IEEE Transctions on Image Processing, 1997, 6(3): 357–372.

[4] Wang Y Y, Xie L H, De Souza C E. Robust control of a class of uncertain nonlinear systems [J]. Systems Control Letters,1992, 19(2): 139–149.

[5] 李晶晶. 不确定时滞系统的稳定性[J]. 科技信息, 2012(35): 25–26.

[6] Guo Y X. Mean-square global asymptotic stability of stochastic recurrent neural networks with distributed delays [J].Applied Mathematics and Computation, 2009, 215(2): 791–795.

[7] Wang Q, Liu X Z. Exponential stability of impulsive cellular neural networks with time delays via Lyapunov functions [J].Applied Mathematics and Computation, 2007, 194(1): 186–198.

[8] He Y, Liu G P, Rees D, et al. Stability analysis for neural networks with time-varying interval delay [J]. IEEE Transctions on Neural Networks, 2007, 18(6): 1 850–1 854.

[9] Huang H, Cao J. Exponential stability analysis of uncertain stochastic neural networks with multiple delays [J]. Nonlinear Analysis: Real World Applications, 2007, 8(2): 646–653.

[10] Wang Z, Lauria S, Fang J, et al. Exponential stability of uncertain stochastic neural networks with mixed time-delays [J].Chaos, Solitons and Fractals, 2007, 32(1): 62–72.

[11] Wang Z D, Fang J A, Liu X H. Global stability of stochastic high-order neural networks with discrete and distributed delays [J]. Chaos,Solitons and Fractals, 2008, 36(2): 388–396.

[12] Liao X X, Mao X R. Stability of stochastic neural networks [J]. Neural, Parallel and Scientific Computations, 2001, 4(2):205–224.

[13] Guo Y X. Mean square global asymptotic stability of stochastic recurrent neural networks with distributed delays [J].Applied Mathematics and Computation, 2009, 215(2): 791–795.

[14] Huang C X, He Y G, Wang H N. Mean square exponential stability of stochastic recurrent neural networks with timevarying delays [J]. Computers and Mathematics with Applications, 2008, 56(7): 1 773–1 778.

[15] Syed Ali M. Stochastic stability of uncertain recurrent neural networks with Markovian jumping parameters [J]. Acta Mathematica Scientia, 2015, 35(5): 1 122–1 136.

[16] Kim J H. Delay and its time-derivative dependent robust stability of time-delayed linear systems with uncertainty [J]. IEEE Transactions on Automatic Control, 2001, 46(5): 789–792.

[17] Liu B, Liu X Z. Robust stability of uncertain discrete impulsive systems [J]. IEEE Transactions on Circuits and Systems II:Express Briefs, 2007, 54(5): 455–459.

[18] Chen W H, Lu X M. Mean square exponential stability of uncertain stochastic delayed neural networks [J]. Physics Letters A, 2008, 372(7): 1 061–1 069.

[19] Yu J J, Zhang K J, Fei S M. Further results on mean square exponential stability of uncertain stochastic delayed neural networks [J]. Communications in Nonlinear Science and Numerical Simulation, 2009, 14(4): 1 582–1 589.

[20] Deng F Q, Luo Q, Mao X R. Stochastic stabilization of hybrid differential equations [J]. Automatica, 2012, 48(9): 2 321–2 328.

[21] Guo Q, Mao X R, Yue R X. Almost sure exponential stability of stochastic differential delay equations [J]. SIAM Journal on Control and Optimization, 2016, 54(4): 1 919–1 933.

[22] Boyd S I, Ghaoui L, Feron E, et al. Linear matrix inequalities in system and control theory [M]. Philadelphia: Society for Industrial and Applied Mathematics, 1994.

[23] Mao X R. Stochastic Differential Equations and Applications [M]. 2nd ed. England: Horwood Publishing Limited, 1997.

[24] Xie L, Fu M, De Souza C E. H∞control and quadratic stabilization of systems with uncertain via output feedback [J].IEEE Transactions on Automatic Control, 1992, 37: 1 253–1 256.

(责任编校: 刘刚毅)

The almost sure exponential stability of uncertain stochastic neural networks

Zhang Jingfa
(School of Mathematics, South China University of Technology, Guangzhou 510640, China)

By constructing a appropriate Lyapunov function, and utilizing Lyapunov functional method, stochastic analysis method and linear matrix inequalities, the sufficient conditions for the almost sure exponential stability of uncertain stochastic neural networks are derived, which can verify the given conditions are satisfied with the lemma.The result shows that the same stability of systems with time-varying delays when time-varying delys are less than a upper bound. The given conditions are in the form of linear matrix inequalities, so it is easy to get its solution by Matlab Toolbox when checking the stability conditions of the systems.

stochastic neural networks; almost sure exponential stability; Lyapunov functions; time-varying delays

TP 183

: A

1672–6146(2017)03–0013–07

10.3969/j.issn.1672–6146.2017.03.004

张景发, 502462024@qq.com。

: 2017–02–22