基于改进即时学习算法的湿法冶金浸出过程建模

牛大鹏，刘元清

（东北大学信息科学与工程学院，辽宁 沈阳 110819）

基于改进即时学习算法的湿法冶金浸出过程建模

牛大鹏，刘元清

（东北大学信息科学与工程学院，辽宁 沈阳 110819）

针对湿法冶金浸出过程中存在的多变量、非线性和多工况等问题，采用基于即时学习算法的最小二乘支持向量机建立浸出率的预测模型。将时间有序性引入到即时学习算法学习集的选取规则中以确定系统当前工作点的建模邻域，从而提高模型精度；引入累计相似因子以提高所建模型的实时性，并利用自适应相似度阈值来判定是否需要重新建立当前工作点的局部模型。将改进的建模方法应用到湿法冶金浸出过程浸出率的预测中，仿真结果表明，所建模型具有较高的精度和实时性，可用于湿法冶金工业生产过程。

湿法冶金；浸出过程；即时学习算法；最小二乘支持向量机；时间有序性；累计相似因子

引 言

湿法冶金具有金属回收程度高、对环境污染较小等显著优点，很适合于处理低品位矿石资源，在我国黄金冶炼生产中具有重要的地位。金的湿法冶金工业生产过程包含浸出、压滤洗涤和置换等多个工序，机理复杂，其准确机理模型的建立非常困难。随着神经网络、支持向量机回归、偏最小二乘回归等建模方法的出现，基于生产过程历史数据的经验模型，近年来得到了广泛应用[1-6]。

在湿法冶金工业过程中，生产工况和设备特性等会随着时间发生变化，如设备老化、催化剂钝化、原材料因生产任务的改变而改变等，因此所建立的经验模型必须随系统特性的变化及时更新，才能准确预测过程特性。实时准确的过程模型是工业生产在线优化和控制等后续研究的基础和前提。

目前，一些学者采用即时学习方法进行基于数据的经验模型研究和过程参数估计，从而使所建模型在工况变化时能够快速自动调整[7-10]。文献[11]提出了一种多模型建模的方法，通过选择更相似的样本集建立即时学习模型以更好地描述当前过程。文献[12]采用多个模型的加权平均对新旧数据进行增减，利用更新局部模型的办法来替代单一的全局模型。文献[13]则提出了在线动态更新模型的方法以替代全局静态模型，取得了较好的效果。然而，目前针对湿法冶金生产过程的建模研究还主要集中在机理模型和离线混合模型等方面。

在基于即时学习[14-18]的建模方法中，学习集的选取和局部模型的建立是最为关键的环节。传统的即时学习算法一般根据数据样本间的空间距离进行学习集的选择，而不考虑数据的时间特性。同时，在进行局部建模时，对每个工作点都重新进行局部建模，建模计算量较大。本文提出将时间有序性引入到即时学习算法中，即根据一定的规则确定每个数据的时间权重，将其应用到即时学习算法数据库的选取规则中，使所选建模数据与当前工作点充分接近，从而提高所建模型的准确性。同时，利用累计相似因子来确定学习集的大小，并基于自适应相似度阈值来判定是否需要重新建立局部模型，以提高算法的实时性。最后，将改进的即时学习策略应用于湿法冶金典型工序——浸出过程[19-21]浸出率的预测以验证其有效性。

1 基于即时学习算法的在线建模方法

与全局学习方法相比，基于即时学习的局部模型在建立时样本数据较少。为了保证所建模型的性能，本文采用适用于小样本数据建模的最小二乘支持向量机[22-26]（LSSVM）来建立局部模型。

与传统的基于数据驱动的建模方法不同，即时学习算法是根据系统当前工况，依据某种准则，从系统大量输入输出的历史信息中找出与该工作点相近的模态，构造算法的学习集，从而实现对当前工作点的估计输出。可以看出，该算法无须事先建立系统的全局模型，而是在线划定当前工作点所属区间(学习集)，并随着工作点的变化，滚动建立系统的若干局部模型，以满足实时测量与控制的需要。

根据当前工作点的输入Xq和历史数据库中的输入Xi计算它们的距离与其夹角大小，公式如下

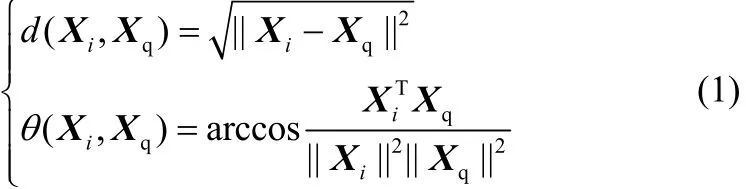
从数据库中选取与当前工作点最靠近的k组数据，构造即时学习集。其历史数据库中的输入数据与当前工作点的相似度计算公式如下

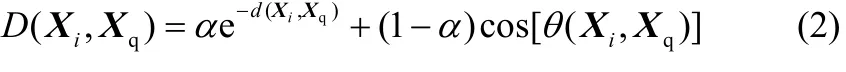
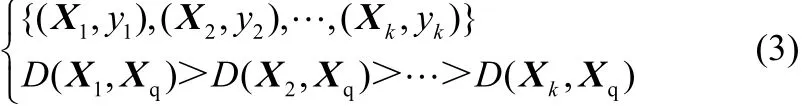
局部建模问题即转化为优化问题

极小化J()δ求得系统当前工作点的模型参数δ，进而可得到其局部模型

最小二乘支持向量机具有计算简单、学习速度快等优点，特别适用于在线建模。在由即时学习算法得到建模所需的数据集后，本文采用最小二乘支持向量机（LSSVM）进行局部建模。对于一组输入样本，LSSVM 利用非线性映射将训数据集映射到一个高维特征空间，从而使非线性函数估计问题转化为高维特征空间中的线性函数估计问题[27-28]。设建模数据集如下

式中，Xq为当前工作点输入，Xi为历史样本输入。

利用LSSVM算法将建模样本数据集映射到高维线性特征空间，并构建局部最优回归函数

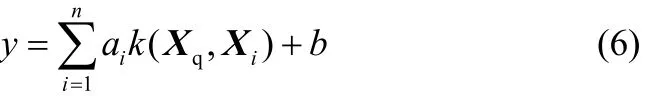
式中，ai为拉格朗日乘子；b为偏差；y为输出；Xq为当前工作点的输入向量为核函数

2 基于时间有序性的即时学习算法

在工业生产中，设备特性和工况等过程特性会随着时间发生变化，因此在选取学习集的时候有必要考虑数据的时间特性。本文将时间有序性引入到即时学习算法中，以获取更为合理的学习集并用于局部模型的构建。

2.1 时间权重的确定

定义 1 时间权向量的熵I。熵是信息的一个度量。熵值越大，则数据所含有的信息量越小。时间权向量的熵反映了对样本的集结过程中权重包含信息的程度。

定义2 时间度。“时间度”的大小体现了对时序的重视程度，即当越小时，表明越注重距离当前工作点较近期的数据；当越大时，表明越注重距离预测时刻较远期的数据。

时间度的赋值规则：当λ=0.1时，说明非常重视近期数据；当λ=0.5时，说明同样重视所有时期数据；当λ=0.9时，说明非常重视远期数据。

W的确定准则：时间权向量 W的确定，既要充分考虑主观的专家经验知识，也要兼顾时间样本点本身所包含的客观信息。因此，论文采用一种主客观相结合的方法来确定时间权向量。时间度根据赋值规则和专家知识选取，W的确定即转化为如下非线性规划问题

2.2 累计相似因子

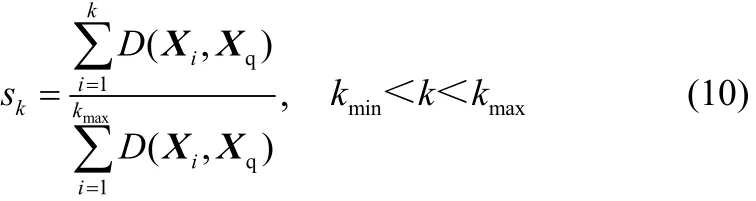
式中，分母表示当前时刻所有与Xq相似样本的相似度总和，分子表示具有最大相似度的前k组样本的贡献之和。与经典的主元分析类似，直接按照贡献度来选择 k，或者设定在贡献度的某一范围内选择k，这样就能获得大部分相似样本。由于sk可以通过相似度将Xq与相似样本集联系起来，比直接选择k具有更明确的意义，从而使得建立局部模型时所选择的样本数据更为合理；同时，累计相似因子的引入也可在一定程度上减小局部模型建立时所需学习集的规模，从而能够提高建模的实时性。

2.3 基于时间有序性的即时学习算法

JIT学习算法解决了寻找全局泛化误差最小模型的难题，提高了建模的灵活性。然而，在实际工业过程中，由于设备特性和生产工况会随着生产过程的进行而改变，若以传统的选取规则从数据库中选取学习集，会影响所建模型的性能。因此，本文针对这一问题，将时间有序性引入到学习集的选择规则中，使学习集的选取更为合理，以提高所建模型的准确性。

基于时间有序性的学习集选取准则

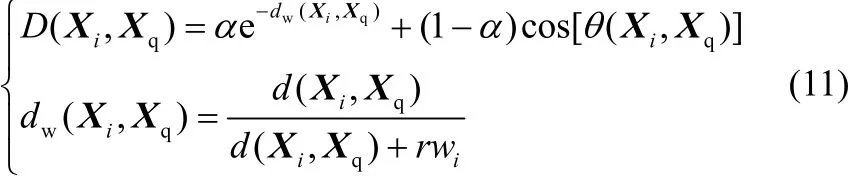
式中，r为可调参数。输入数据Xq变化不大时可选择较大的r值；输入数据Xq变化较剧烈时可选择较小的r值。

算法过程具体如下：

（1）由式（1）计算当前工作点的输入Xq与历史数据的输入Xi的距离和余弦值；

（2）若余弦值小于零，则舍弃这个历史数据；

（3）利用2.1节中时间权重的确定方法得到各个信息向量的时间权重值；

（4）根据事先确定的累计相似因子，利用式（10）确定即时学习集的大小；

（5）根据式（11）的选取准则确定学习集；

（6）利用LSSVM进行建模，得到局部模型。

3 基于自适应相似度阈值的模型更新

即时学习算法对于每个输入数据都需要重新建立局部预测模型，导致计算量较大，模型更新频繁。由于连续生产过程的工作条件不会发生频繁的大范围变化，本文基于相似度阈值判定是否进行重新建模以更新局部模型，从而降低计算量，提高算法的实时性，即：首先基于自适应思想对相似度阈值进行动态确定，若当前工作点的相似度小于所确定的阈值，则说明系统动态特性变化缓慢或已在当前工况稳定工作，此时保留前一时刻所建立的局部模型，并利用投影算法[30]预测当前时刻的输出，而无须重新建立局部模型。具体描述如下：

假定当前工作点时刻为t，输入为Xt。将相似度阈值预先设定为一个小正数，即D*=。计算Xt与前一时刻工作点Xt-1的相似度指数，若，则不更新局部模型，此时利用投影算法来计算当前工作点的输出

式中，y*为系统的期望输出，可用学习集中样本的平均值代替。

基于相似度阈值判定是否重新建立局部模型的具体步骤如下：

（1）初始化相似度阈值，令D*=， 为小正数；

（3）利用更新后的模型对当前工作点的输出进行预测；

（4）读取下一时刻的工作点；

（5）重复步骤（2）～步骤（4）。

4 湿法冶金浸出过程建模

湿法冶金是利用某种溶剂对原料中的金属进行提取和分离的冶金过程。浸出过程是湿法冶金的重要生产工序，浸出液的质量直接决定了后续生产工序的质量。浸出率是浸出过程重要的生产指标，直接影响整个湿法冶金生产过程的有价金属回收率，从而对整体产量、生产效率等指标产生影响。目前浸出率的检测方法大多是离线化验检测，检测时间长、成本高。因此，建立浸出率的预测模型对湿法冶金生产过程的质量检测及控制具有重要的意义。

正常工况下，浸出率是矿石流量、矿浆浓度、矿石平均粒径、固相中初始金品位、流入矿浆中氰离子浓度、溶解氧浓度和氰化钠添加量的函数，即

式中，e为浸出率，Qs为矿浆流量（↓），Cw为矿浆浓度（↑），d为矿石平均粒径（↓），Cs0为固相中初始金品位，Co为溶解氧浓度（↑），QCNi为第i个浸出槽的氰化钠添加量（↑）。考察各因素对浸出率的影响关系，↑表示浸出率随影响因素的增大而增大，↓表示浸出率随影响因素的增大而减小。

矿石粒径可以通过分析原料得到。由于通常使用同一厂家的原料，本文中将其看作常数。初始氰离子浓度的不足可以通过后续氰化钠的添加来弥补，对浸出率的影响较小，本文将其忽略。最终将建模样本的输入向量确定为局部模型的输出即为浸出率e。

本文通过实验对改进的即时学习算法进行验证，并与传统的基于相关性的即时学习策略进行对比。验证所使用的数据来自湿法冶金半实物仿真平台，它是由课题组在工业现场研究开发的浸出率预测系统，已经应用到实际的生产当中，获得了较好的实际应用效果。实验的样本是通过该系统收集了两个运行月的过程有关运行数据, 其中矿浆流量、矿浆浓度和溶解氧浓度是在线测量的，而由于仪器仪表及生产成本的限制，氰离子浓度是通过采样然后进行离线化验的，采样间隔为2 h。将收集到的运行数据分为两组，一组用于训练，一组用于测试验证。由于生产过程比较平稳，采样数据没有太大波动，所以根据专家知识，并经多次仿真实验对比确定相关参数如下：α=0.7，λ=0.4，r=0.4。

实验一：选取300组数据作为样本集，30组数据作为测试样本进行仿真验证。LSSVM 建模过程中相关参数采用交叉验证法确定。预测结果如图 1所示。模型预测性能采用最大相对误差（EMAX）、均方根误差（RESE）和相对均方根误差（RRMSE）进行评价。基本即时学习算法所建模型与改进即时学习算法所建模型误差对比如表1所示。

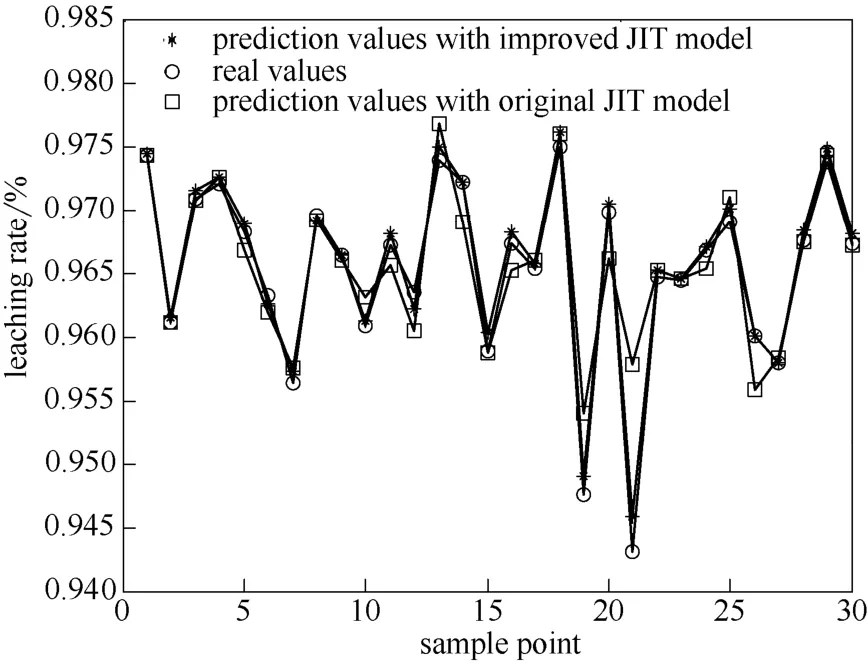
图1 浸出率预测结果Fig.1 Leaching rate prediction results

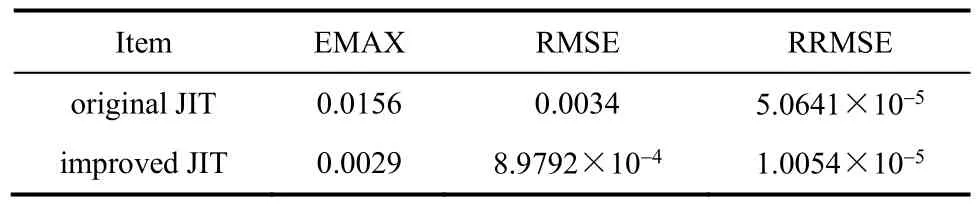
表1 模型性能评价Table 1 Model performance evaluation

从表1中可以看出，基于时间有序性的即时学习算法所建模型的预测值，其最大相对误差、均方根误差、相对均方根误差都要明显小于采用基本即时学习算法所建的模型。通过比较图1所示的预测仿真曲线，也可以看出基于改进即时学习算法的模型预测曲线对浸出率的拟合效果比改进前得到了明显改善。因此，改进的基于时间有序性的即时学习算法提高了建模的准确性。

实验二：选取N(N＞100)组数据，其中后30组数据作为测试样本，来验证改进的模型更新策略的有效性。N为300时的预测结果如图2所示，基本即时学习算法所建模型与基于时间有序性实时的即时学习算法所建模型误差对比如表2所示。

从图2和表2中可以看出，采用基于时间有序性的改进即时学习算法所建模型的预测值比采用基本即时学习算法所建模型的预测值更准确。

当N为400、700、1000、1300和1600时，引入时间有序性和基于自适应相似度阈值的模型更新策略后，改进的即时学习算法建模所用时间和基本的即时学习算法建模所用时间的对比如表 3所示。可见，改进算法建模所用时间比基本算法有所减少，虽然在数据库规模不大时表现不明显，但当数据库大于1000时，改进算法建模用时远小于基本算法。

综上，改进的即时学习算法能够在保证模型准确性的前提下提高建模的实时性，特别是当历史数据库规模较大时，改进算法建模的实时性体现得更为明显。

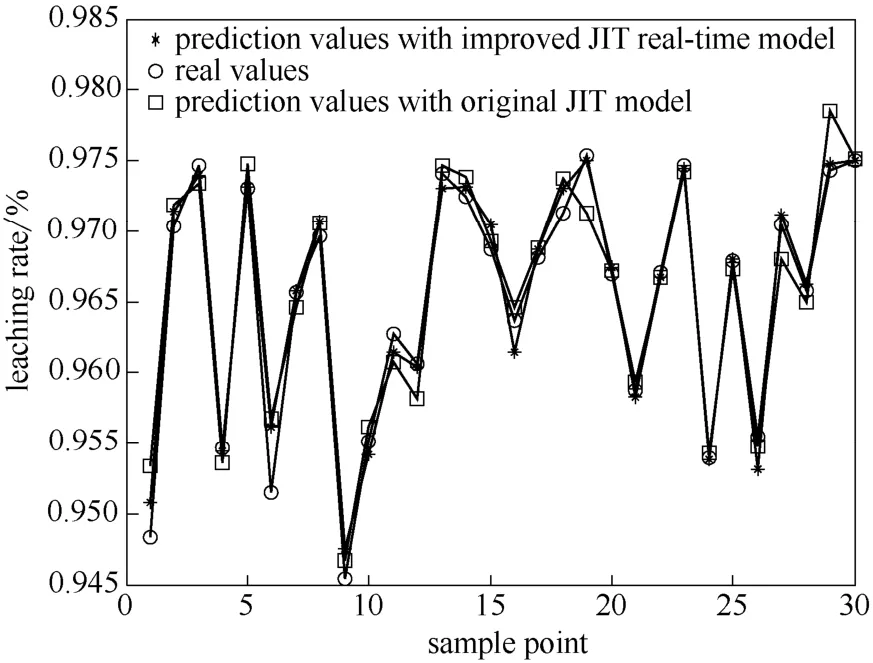
图2 N为300时的浸出率预测结果Fig.2 Leaching rate prediction results when N is 300

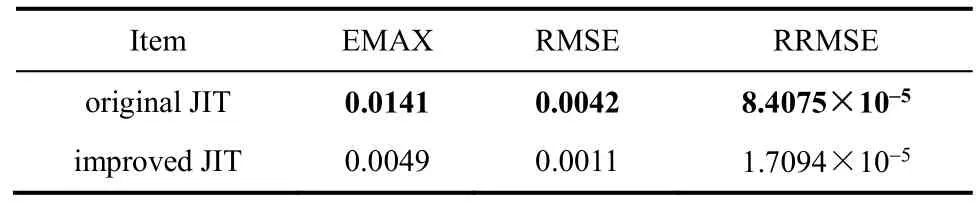
表2 模型性能评价Table 2 Model performance evaluation

表3 改进前后的算法建模时间对比Table 3 Cost time of modeling based on improved algorithm and basic JIT

5 结 论

本文将时间有序性引入即时学习算法，结合时间权重计算历史数据与当前工作点的相似度用于学习集的选取，并引入累计相似因子来确定学习集的规模，提高了所建模型的准确性和实时性。同时，为了克服基本即时学习算法计算量大、耗时较长等缺点，基于自适应相似度阈值来确定是否重新进行局部建模，若当前输入数据与局部模型对应的工况接近，则保留前一时刻基于即时学习算法所建立的局部模型，并利用投影算法计算当前时刻的预测输出，而当生产工况变化时则利用改进的即时学习算法重新进行局部建模以更新模型，从而在保证所建模型准确性的前提下提高了建模的实时性。在湿法冶金浸出过程中的仿真验证表明，本文所提出的改进即时学习算法比基本的即时学习算法具有更好的性能，可用于湿法冶金实际工业生产之中。

[1] CHENG L, LIU W, HOU Z G, et al. Neural network based nonlinear model predictive control for piezoelectric actuators [J]. IEEE Transactions on Industrial Electronics, 2015, 62 (12)： 1-1.

[2] ZHAO C H, WANG F L, GAO F R, et al. Adaptive monitoring method for batch processes based on phase dissimilarity updating with limited modeling data [J]. Industrial & Engineering Chemistry Research, 2007, 46 (14)： 4943-4953.

[3] FENG K, LU J, CHEN J. Nonlinear model predictive control based on support vector machine and genetic algorithm [J]. Chinese Journal of Chemical Engineering, 2015, 23 (12)： 2048-2052.

[4] ZHAO C H, WANG F L, LU N Y, et al. Stage-based soft-transition multiple PCA modeling and on-line monitoring strategy for batch processes [J]. Journal of Process Control, 2007, 17 (9)： 728-741.

[5] LIU Z T, FENG Z H. Research on two-dimensional landslide model control system based on support vector machine modeling [J].Applied Mechanics & Materials, 2014, 580-583： 947-953.

[6] LIU R L. Modeling soft sensor based on support vector machine and particle swarm optimization algorithms [J]. Control Theory &Applications, 2006, 23 (6)： 895-894.[7] ZHAO C H, GAO F R. Online fault prognosis with relative deviation analysis and vector autoregressive modeling [J]. Chemical Engineering Science, 2015, 138 (22)： 531-543.

[8] ZHANG X, LI Y, KANO M. Quality prediction in complex batch processes with just-in-time learning model based on non-Gaussian dissimilarity measure [J]. Industrial & Engineering Chemistry Research, 2015, 54 (31)： 7694-7705.

[9] 綦欢, 叶贞成, 钱锋,等. 乙烯裂解炉燃料气消耗的实时优化 [J].计算机与应用化学, 2015, 32 (12)： 1457-1461.QI H, YE Z C, QIAN F, et al. Real-time optimization for fuel gas consumption of ethylene cracking furnace [J]. Computers and Applied Chemistry, 2015, 32 (12)： 1457-1461.

[10] 周丽春, 靳鑫, 刘毅,等. 即时局部建模在填料塔液泛气速预测的应用 [J]. 化工学报, 2016, 67 (3)： 1070-1075.ZHOU L C, XIN X, LIU Y, et al. Just-in-time local modeling for flooding velocity prediction in packed towers [J]. CIESC Journal,2016, 67 (3)： 1070-1075.

[11] 罗健旭, 邵惠鹤. 应用多神经网络建立动态软测量模型 [J]. 化工学报, 2003, 54 (12)：170-177.LUOJ X, SHAO H H. Developing eveloping dynamic soft sensors usingmultipleneural networks [J]. Journal of Chemical Industry and Engineering (China), 2003,54(12)： 170-177.

[12] DU W L, GUAN Z Q, QIAN F. The time series soft-sensor modeling based on Adaboost LS-SVM[C]//The 8th World Congress on Intelligent Control and Automation (WCICA),Jinan, 2010： 1491-1495.

[13] WANG H Q, LI P, GAO F R, et al. Kernel classifier with adaptive structure and fixed memory for process diagnosis [J]. AIChE Journal,2006, 52 (10)： 3515-3531.

[14] BONTEMPI G，BIRATTARI M, BERSINI H. Lazy learning for local modeling and control design [J]. International Journal of Control,1999,72 (7/8)： 643-658.

[15] USHIDA S, KIMURA H. Just-in-time approach to nonlinear identification and control [J]. Journal of SICE, 2005, 44 (2)： 102-106.

[16] PAN T H, LI S Y, WANG X. A multi-model modeling approach to nonlinear systems based on lazy learning[C]//Proceedings of the 24th Chinese Control Conference. 2005： 268-73.

[17] LIU Y, GAO Z L, LI P, et al. Just-in-time kernel learning with adaptive parameter selection for soft sensor modeling of batch processes [J]. Industrial and Engineering Chemistry Research, 2012,51 (11)： 4313-4327.

[18] SU Q L, MARTIN W H, RICHARD D B, et al. Just-in-time-learning based extended prediction self-adaptive control for batch processes [J].Journal of Process Control, 2016, 43： 1-9.

[19] LIMA L R P D A, HODOUIN D. Simulation study of the optimal distribution of cyanide in a gold leaching circuit [J]. Minerals Engineering, 2006, 19 (13)： 1319-1327.

[20] LIAM L R P D A. Some remarks on the reactor network synthesis for gold cyanidation [J]. Minerals Engineering, 2006, 19 (2)： 154-161.

[21] HU G, MAO Z Z, HE D K, et al. Hybrid modeling for the prediction of leaching rate in leaching process based on negative correlation learning bagging ensemble algorithm [J]. Computers & Chemical Engineering, 2011, 35 (12)： 2611-2617.

[22] LIU Y, WAN H Q, LI P. Adaptive local learning based least squares support vector regression with application to online modeling for fermentation processes [J]. Journal of Chemical Industry and Engineering,2008, 59 (8)： 2053-2057.

[23] GE Z Q, SONG Z H. A comparative study of just-in-time-learning based methods for online soft sensor modeling [J].Chemometrics and Intelligent Laboratory Systems, 2010, 104 (2)： 306-317.

[24] NIU D P, SUN Y, WANG F L. Optimization of advertising budget allocation over time based on LS-SVMR and DE [J]. Automation Science &Engineering IEEE Transactions on, 2014, 10 (4)：1076-1082.

[25] LIN W Q, JIAN-ZHONG F U, YA-ZHOW X U, et al. Thermal error modeling &compensation of numerical control machine tools based on on-line least squares support vector machine [J]. Computer Integrated Manufacturing Systems, 2008, 14 (2)： 295-299.

[26] SUN L, YU F, ZHANG D, et al. Online modeling for wood drying based on least squares support vector machine [J]. Chinese Journal of Scientific Instrument, 2009, 30 (9)： 1991-1995.

[27] SERAFINI T, ZANGHIRATI G, ZANNI L. Gradient projection methods for quadratic programs and applications in training support vector machines [J]. Optimization Methods & Software, 2005, 20(2/3)： 353-378.

[28] 葛志强, 刘毅, 宋执环. 一种基于局部模型的非线性多工况过程检测方法 [J]. 自动化学报, 2008, 34 (7)： 792-797.GE Z Q, LIU Y, SONG Z H. Local model based monitoring for nonlinear multiple mode process [J]. Acta Automatica Sinica, 2008,34 (7)： 792-797.

[29] 刘毅, 金福江, 高增梁. 时变过程在线辨识的即时递推核学习研究 [J]. 自动化学报, 2013, 39 (5)： 602-609.LIU Y, JIN F J, GAO Z L. Online identification of time-varying processes using just-in-time recursive kernel learning approach [J].Acta Automatica Sinica, 2013, 39 (5)： 602-609.

[30] 孙维, 王伟, 朱瑞军. 即时学习算法在非线性系统迭代学习控制中的应用 [J]. 控制与决策, 2003, 18 (3)： 263-266.SUN W, WANG W, ZHU R J. Iterative learning control for nonlinear system using lazy learning method [J]. Control and Decision, 2003,18 (3)： 263-266.

Modeling hydrometallurgical leaching process based on improved just-in-time learning algorithm

NIU Dapeng, LIU Yuanqing
(School of Information Science & Engineering, Northeastern University, Shenyang 110819, Liaoning, China)

Least squares support vector machine (LS-SVM) based on just-in-time (JIT) learning algorithm was used to build prediction model of leaching rate, when considered multi-variable multi-mode nonlinear characteristics of hydrometallurgical leaching process. Time order was introduced into selection rule of JIT learning set for the determination of modeling neighborhood of current operating point, so as to improve modelling accuracy. A cumulative similarity factor was adopted to improve real-time performance of the model and an adaptive similarity threshold was used to determine necessity of updating local model of the current operating point. The simulation results for hydrometallurgical leaching process show that the improved modeling method has high precision and good real-time performance in leaching rate prediction, which can be used in hydrometallurgical industrial production.

hydrometallurgy; leaching process; just-in-time learning algorithm; least squares support vector machine; time order; cumulative similarity factor

date：2016-12-23.

NIU Dapeng, niudapeng@ise.neu.edu.cn

supported by the National Natural Science Foundation of China (61673092, 61304121, 61533007) and the Fundamental Research Funds for the Central Universities (N150404017).

TP 301.6

A

0438—1157（2017）07—2873—07

10.11949/j.issn.0438-1157.20161803

2016-12-23收到初稿，2017-03-24收到修改稿。

联系人及第一作者：牛大鹏（1980—），男，副教授。

国家自然科学基金项目（61673092，61304121，61533007）；中央高校基本科研业务费专项资金（N150404017）。