间歇过程点对点迭代学习控制的初始状态误差分析
洪英东,熊智华,江永亨,叶昊
(清华大学自动化系,北京 100084)
间歇过程点对点迭代学习控制的初始状态误差分析
洪英东,熊智华,江永亨,叶昊
(清华大学自动化系,北京 100084)
针对间歇过程点对点跟踪控制问题,在轨迹更新的迭代学习控制算法框架下,针对非理想初始状态情况下3种不同的初始误差,通过2D Roesser模型对其进行描述并分析其收敛性。给出了不同的情况下系统相对参考轨迹的零误差跟踪或者收敛到特定邻域的条件,在零误差跟踪不能实现的情况下给出了邻域的范围。通过数值模型仿真验证了给出的收敛条件和收敛边界,并分析了不同因素对收敛边界的影响。
初始状态;迭代学习控制;2D系统理论;点对点跟踪
引 言
由于多样化和精细化工的需求,间歇过程在工业生产中的比例越来越高[1]。由于间歇过程具有重复运行等特性,迭代学习控制(ILC)方法得到了广泛的研究[2-3]。ILC方法通常是跟踪一条预设的完整轨迹,但是在很多应用中,比如快速热处理过程[4]、发酵过程[5]等,都只要求跟踪整条轨迹中若干特定时间点的输出。因此,点对点ILC控制成为了目前的一个研究热点[6-7]。间歇过程的ILC方法通常假设每个批次的初始状态满足理想条件,即系统在每个批次的初始状态误差均为零。但是在间歇式反应生产过程中,由于每个批次的反应物初始浓度等条件往往会产生一定的偏差,因此通常难以满足该初始状态理想条件。
有很多的学者讨论过,在初始条件非理想的情况下,迭代学习控制算法可能发散的问题[8]。针对全轨迹跟踪问题中初始状态非理想的情况,Park等[9]分析了P型和PID型迭代学习控制算法的跟踪误差和初始状态误差边界的关系。孙明轩[10]提出了带初始误差校正的迭代学习控制算法,Chi等[11]提出了一种针对随机初始状态的自适应迭代学习控制算法,这些算法都解决了一些特定初始误差情况下的跟踪误差问题。同时,因为批次过程既有时间方向的特性,又有批次方向的特性,2D模型也常常被引入对迭代学习控制算法进行分析[12-13]。Fang等[14]采用2D理论对不同初始状态下的迭代学习控制方法进行了收敛性分析,其收敛性条件中要求批次和时间都趋于无穷,但是在重复运行的过程中,时间通常是有限的,这一点一般不能够得到满足。Guan等[15]针对连续系统,通过采样的2D离散模型分析了初始状态误差模和有界的PD型迭代学习算法的收敛情况。对于线性时变的2D系统的一般性收敛条件分析,Li等[16]、Meng等[17]分析了在初始误差有界的情况下,在2D Roesser模型下的传递函数矩阵模的上确界存在且小于 1,系统的误差有界。之后Meng等[18]进一步分析了初始误差趋于0时系统跟踪误差的收敛情况。不过他们的分析结果都仅考虑了初始误差有界和误差趋于零的情况,也没有给出明确的收敛界。而且均没有针对点对点跟踪问题进行分析。
目前的点对点跟踪问题研究,主要集中于利用非跟踪点自由度来加快收敛速度[19-20],而缺少对初始状态误差的分析。对于这一问题,针对线性时不变系统,采用2D模型理论分析了不同初始条件下,针对系统相对于更新的参考轨迹的所有时间点的误差,算法的收敛判定条件和收敛界,并进一步通过数值仿真验证了本文的理论。
1 点对点迭代学习控制
1.1 系统描述
考虑如下线性时不变间歇过程的一般状态空间模型

其中,t和k分别代表采样时间和运行批次,t∈[0, N],N为采样点数,x∈RN、u∈R、y∈R分别为系统的状态、输入和输出,A、B、C分别为相应的系统参数矩阵,d代表过程干扰和测量噪声。
对于点对点ILC问题,其控制目标为在特定的时间点集M={t1,t2,…,tM},M ≤ N,要求输出跟踪给定值ydM=[yd(t1),…,yd(tM)]T。
针对上述点对点ILC问题,选取的方法是设计一条经过这些目标点的轨迹并在批次间对其进行更新。轨迹更新的基本思想是在关键时间点轨迹不变,而在非关键点上根据上一个批次的输出信息进行调整,采用如下的插值算法来更新轨迹[21]

其中,rk=[r(1,k),…,r(N,k)]T为第 k批次在所有时间点上的参考轨迹,Λk=diag{λk(1), λk(2),…, λk(N)},λk(t)为各采样时刻的轨迹更新系数,且λk(t)在 t∈M时取0,其他时间点上选取合适的值,使其满足[22]

其中yk=[y(1,k),…,y(N,k)]T为第k批次在所有时间点上的输出。
在批次间,选取常用的P型迭代学习控制算法

其中uk=[u(0,k),…,u(N-1,k)]T,ek=rk-yk,且ek=[e(1,k),…,e(N,k)]T为全轨迹的跟踪误差,L为学习率。
在点对点ILC问题中,只需要关心特定点集M上的跟踪误差ekM,可知ekM是ek一个子集,记为

其中


所以点对点问题的跟踪误差可以写成
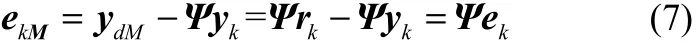
1.2 2D模型描述
根据系统的状态方程式(1)和跟踪误差关系式(6),并结合P-ILC的学习律式(4),可以把上述系统模型描述成一个2D Roesser模型[21]

其中

通过上述变换表述的2D Roesser模型,由于式(2)中更新轨迹参数λk(t)的引入,而且λk(t) 随着时间t变化,因此与一般的基于2D理论的迭代学习控制模型不同之处是参数为时变的,因此其状态转移矩阵特性也有相应的变化。
1.3 初始状态描述
假设理想初始状态为xr(0),则记第k批次的初始状态误差为Δx(0,k)=x(0,k)-xr(0)。Xu等[23]在分析初始状态问题时,给出了理想初始状态、和有界、固定偏差、随机有界偏差、队列偏差5种不同的情况。对于以上5种初始状态情况,在2D模型中重新对其进行描述,可以分为4类情况。
(a)批次间状态误差为0,即η(0,k)=0。该情况既包括初始状态理想,也包括初始状态非理想,但每次偏差均相同的情况。
(b)批次间误差模有界,即||η(0,k)||≤C。如发酵过程设定的初始温度,总是在期望温度的附近波动,则其误差的模有界[24]。
(d)队列偏差,即 x(0,k)=x(N,k-1),是指当前批次的初始状态为上一批次的结束状态[26]。
因为在化工生产间歇过程中,通常会在新批次开始时重置初始条件,不满足队列偏差的条件,因此下文主要讨论前3种初始误差情况。
2 收敛条件分析
在证明收敛条件以前,首先证明时变2D系统的一些性质。为方便起见,记
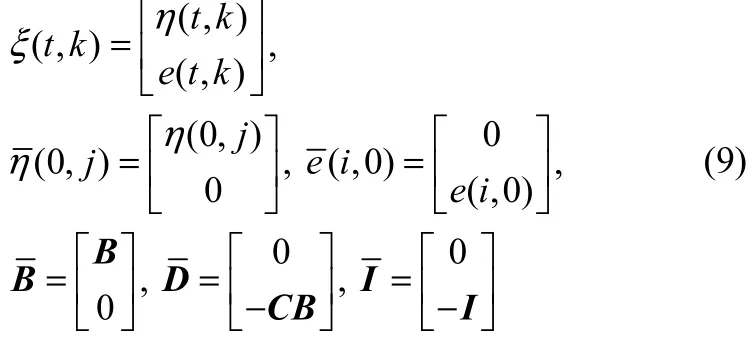
定义2D模型(8)中状态转移矩阵为

并定义如下状态转移矩阵

由2D理论可知[21]

并根据文献[27]的2D Roesser模型理论可以得到系统的全响应为

同时,根据之前的工作,还得到了如下时变2D系统状态转移矩阵的性质[28]。

根据以上的3个时变2D系统的性质,可以分析得到在2D系统下3种初始状态存在误差的收敛条件和收敛边界。在分析初始误差的影响情况下,假设过程干扰Δd(t,k) 都为0。
2.1 批次间无初始状态误差
证明:根据全响应公式(13),可得


定理1说明,在批次间无初始状态误差的情况下,只要转移矩阵在任意 t时刻都成立,则均可以实现零误差跟踪。
2.2 批次间初始状态误差有界
证明:同样根据全响应公式(13),可得
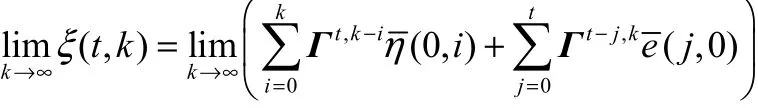
又因为||η(0,k)|| ≤C,则可得


进一步可得

定理2说明,在批次间初始状态误差有界的情况下,只要转移矩阵||||<1在任意 t时刻成立,系统跟踪误差会收敛到零附近的一个较小邻域内,且该邻域的范围大小由||Γ0,1||、|||和C 3个因素决定。
2.3 批次间误差模和有界
证明:根据定理2的证明可知

取 n3=2max(n1,n2),则当 n>n3时

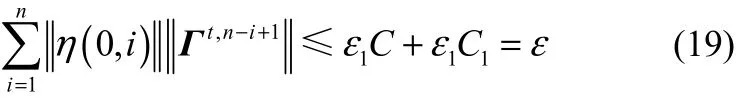
即∀ε,∃n3,满足当 n>n3时,
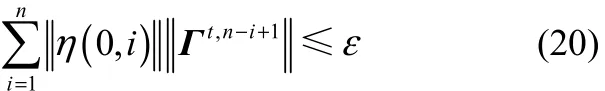
根据极限性质可得
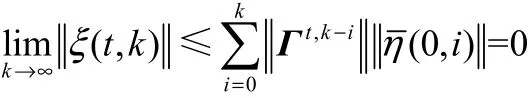
定理3说明,在批次间初始误差的模和有界的情况下,只要转移矩阵|||<1在任意t时刻成立,系统可以实现零误差跟踪。
根据全响应公式[式(13)],再根据线性系统的叠加性原理,可以知道,对于存在批次间干扰的情况,分析仍然适用,只需要再单独考虑过程干扰的影响即可。
3 数值仿真
一些典型的间歇反应过程,如以温度为调节量、产物为被控量的间歇反应过程[29-30],通过对其几个批次的输入输出数据进行系统辨识,可以将其描述成二阶线性状态空间模型。
选取如下的二阶线性非时变系统作为数值仿真实例[21]
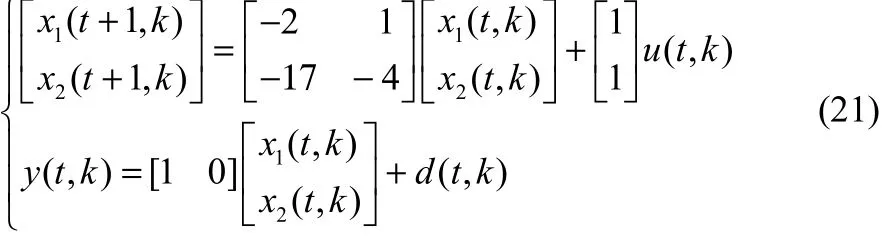
初始的输入为u(t,1)=0,∀t。仿真时间为5 s,采样时间为0.125 s,则采样点N为40。过程干扰取为[-0.01, 0.01]之间的平均分布。
选取的跟踪时间点集为M={1,10,15,25,31,40},图1给出了关键点跟踪目标和初始轨迹,跟踪目标为一个上升、保持、下降的过程,在热处理过程等间歇过程中较为典型。

图1 跟踪目标和初始轨迹Fig1 Key points and initial trajectory
采用如下的跟踪误差平方值来判断方法的性能

首先,把初始误差理想条件(包括初始状态为理想值和初始状态始终为同一偏差值)与初始状态误差有界的情况进行了仿真对比。
在误差界Bd为0时,即为初始误差理想情况。另外则为初始误差随机,但其模分别小于误差界Bd为 0.03和 0.06的两种情况(图 2)。控制律L=3,λ(t)=-0.65,此时的收敛条件为||||=0.9571<1。
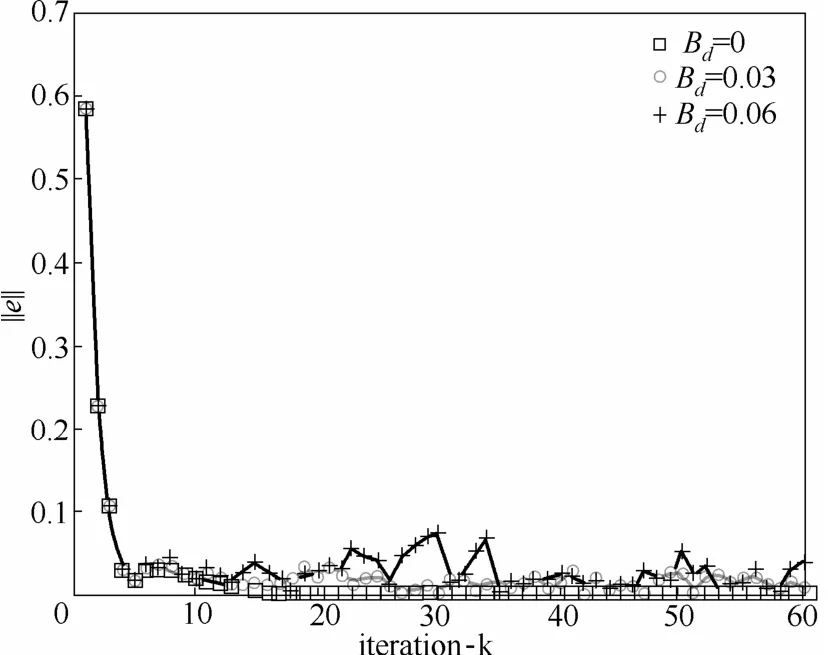
图2 批次间误差有界和误差为0的比较Fig.2 Comparison of bounded initial errors
可以看到,在初始状态误差有界的情况下,在轨迹更新的一般迭代学习控制律算法下,点对点ILC问题虽然不能实现零误差跟踪,但是其误差在与初始状态误差边界有关的一个小邻域内。
而在初始状态误差恒定,即批次间的初始状态变化为0的情况下,跟踪误差收敛到0。
通过对初始状态误差有界情况的分析可知,在同样的误差边界的情况下,收敛界的大小和||||的大小有关。|||的大小可以通过算法的学习律和轨迹更新参数来调整。因为||||代表了所有t时刻中单步转移矩阵模的最大值,因此如果要使得||||变小,首先要调节迭代学习控制律,使得其在关键点变小,再调节轨迹更新参数λ(t)即可。
图3给出了当误差界为Bd=0.06时,在满足收敛性条件的情况下,不同的|||对应的跟踪误差ekM收敛曲线。
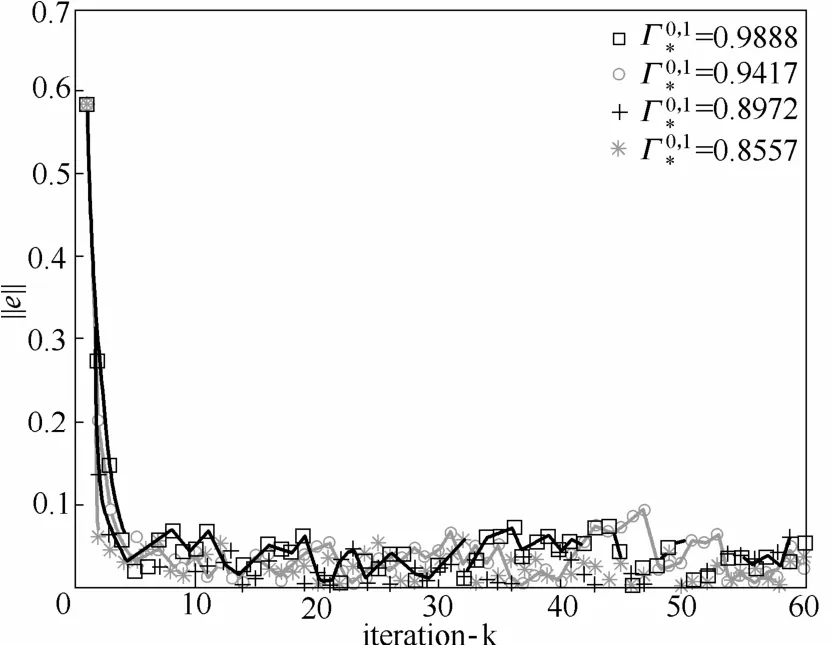
图 3 ||||对收敛界的影响Fig.3 Effects of ||| on convergence
对于误差模和有界的情况,取初始状态误差的形式为以下3种:

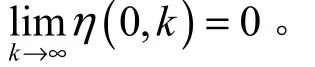
图4给出了上述3种情况下的仿真结果。

图4 误差和有界仿真Fig.4 Sequence of initial errors belong to l2
由图 4结果可以看出,在情况(iii)中,系统的跟踪误差收敛到0。而在(i)和(ii)的情况下,跟踪误差不为0,而是在0的一个邻域内。
说明当初始状态误差趋于零时,不能保证跟踪误差收敛到 0,只能保证误差收敛到一个有界的邻域内,而在误差模和有界的情况下,才能够保证误差收敛到0。
4 结 论
针对间歇过程点对点ILC问题,在轨迹更新的迭代学习控制算法下,基于二维线性系统理论,分析了3种初始条件情况下的收敛条件。
在批次间初始状态误差为零、误差和有界的情况下,可以通过算法参数设置使得跟踪误差收敛到零。在初始状态误差有界的情况下,证明了算法能够收敛到一个零附近的邻域的条件。
分析了如果不能够实现零误差跟踪,其收敛界的影响因素,也为针对初始误差情况下迭代学习控制算法的参数设计提供了准则。
[1] 宋建成. 间歇过程计算机集成控制系统. 北京: 化学工业出版社,1999.SONG J C. Computer Integrated Control System for Batch Process[M].Beijing: Chemical Industry Press, 1999.
[2] LEE J H, LEE K S. Iterative learning control applied to batch processes: an overview[J]. Control Engineering Practice, 2007,15(10): 1306-1318.
[3] 贾立, 施继平, 邱铭森. 一种间歇过程产品质量迭代学习控制策略[J]. 化工学报, 2009, 60(8): 2017-2023.JIA L, SHI J P, QIU M S. A novel iterative learning control for product quality control in batch process[J]. CIESC Journal, 2009,60(8): 2017-2023.
[4] CHI R, WANG D, HOU Z, et al. Data-driven optimal terminal iterative learning control[J]. Journal of Process Control, 2012, 22(10):2026-2037.
[5] 王志文, 刘毅, 高增梁. 时变间歇过程的 2D-PID 自适应控制方法[J]. 化工学报, 2016, 67(3): 991-997.WANG Z W, LIU Y, GAO Z L. 2D-PID adaptive control method for time-varying batch processes[J]. CIESC Journal, 2016, 67(3):991-997.
[6] ALHAZZA K A, HASAN A M, ALGHANIM K A, et al. An iterative learning control technique for point-to-point maneuvers applied on an overhead crane[J]. Shock and Vibration, 2014, (1): 261-509
[7] FREEMAN C T. Constrained point-to-point iterative learning control with experimental verification[J]. Control Engineering Practice, 2012,20(5): 489-498.
[8] LEE K H, BIEN Z. Initial condition problem of learning control[J].IEE Proceedings D-Control Theory and Applications, 1991, 138(6):525-528.
[9] PARK K H, BIEN Z. A generalized iterative learning controller against initial state error[J]. International Journal of Control, 2000,73(10): 871-881.
[10] 孙明轩. 初态学习下的迭代学习控制[J]. 控制与决策, 2007, 22(8):848-852.SUN M X. Iterative learning control with Initial state learning[J].Control and Decision. 2007, 22(8): 848-852.
[11] CHI R, HOU Z, XU J. Adaptive ILC for a class of discrete-time systems with iteration-varying trajectory and random initial condition[J]. Automatica, 2008, 44(8): 2207-2213.
[12] KUREK J E, ZAREMBA M B. Iterative learning control systhesis based on 2-D system theory[J]. IEEE Transactions on Automatic Control, 1993, 38(1): 121-125.
[13] GENG Z, JAMSHIDI M. Learning control system analysis and design based on 2-D system theory[J]. Journal of Intelligent &Robotic Systems, 1990, 3(1): 17-26.
[14] FANG Y, CHOW T W S. 2-D analysis for iterative learning controller for discrete-time systems with variable initial conditions[J]. IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications, 2003, 50(5): 722-727.
[15] GUAN W, ZHU Q, WANG X D, et al. Iterative learning control of linear continuous systems with variable initial states based on 2-D system theory[C]//Control Conference (CCC), IEEE, 2014:8812-8815.
[16] LI X D, HO J K L, CHOW T W S. Iterative learning control for linear time-variant discrete systems based on 2-D system theory[J].IEE Proceedings-Control Theory and Applications, 2005, 152(1):13-18.
[17] MENG D, JIA Y, DU J, et al. Necessary and sufficient stability condition of LTV iterative learning control systems using a 2-D approach[J]. Asian Journal of Control, 2011, 13(1): 25-37.
[18] MENG D, JIA Y, DU J. Stability of varying two-dimensional Roesser systems and its application to iterative learning control convergence analysis[J]. IET Control Theory & Applications, 2015, 9(8):1221-1228
[19] OWENS D H, FREEMAN C T, CHU B. Generalized norm optimal iterative learning control with intermediate point and sub-interval tracking[J]. International Journal of Automation and Computing, 2015,12(3): 243-253.
[20] CHU B, FREEMAN C T, OWENS D H. A novel design framework for point-to-point ILC using successive projection[J]. IEEE Transactions on Control Systems Technology, 2015, 23(3):1156-1163.
[21] 洪英东, 熊智华, 邱伟伟, 等. 基于 2D理论的点对点轨迹更新综合预测迭代学习控制[C]//第 27届中国过程控制会议(CPCC2016),2016.HONG Y D, XIONG Z H, QIU W W, et al. Two-dimensional based point-to-point reference trajectory updating integrated predictive iterative learning control for batch process[C]//Chinese Process Control Conference 2016, 2016.
[22] AN T J. Closed loop iterative learning control for point to point tracking problem with desired trajectory updating[J]. Information Technology Journal, 2014, 13(5): 859-863.
[23] XU J X, YAN R. On initial conditions in iterative learning control[J].IEEE Transactions on Automatic Control, 2005, 50(9): 1349-1354.
[24] 张华. 迭代学习控制问题初态研究[D].无锡: 江南大学, 2014.ZHANG H. Research of initial state for iterative learning control[D].Wuxi: Jiangnan University, 2014.
[25] SUN M X. Robustness of higher-order p-type learning control[J]. IET Control Theory & Applications, 1997, 14(1): 12-18.
[26] YANG, Z, CHAN C W. Conditional iterative learning control for non-linear systems with non-parametric uncertainties under alignment condition[J]. IET Control Theory & Applications, 2009, 3(11):1521-1527.
[27] ROESSER R. A discrete state-space model for linear image processing[J]. IEEE Transactions on Automatic Control, 1975, 20(1):1-10.
[28] CHEN C, XIONG Z, ZHONG Y. Design and analysis of integrated predictive iterative learning control for batch process based on two-dimensional system theory[J]. Chinese Journal of Chemical Engineering, 2014, 22(7): 762-768.
[29] RAY W H. Advanced Process Control[M]. New York: McGraw-Hill,1981.
[30] LOGSDON J S, BIEGLER L T. Accurate solution of differential-algebraic optimization problems[J]. Ind. Eng. Chem. Res.,1989, 28(11): 1628-1639.
Analyze initial state errors of point-to-point iterative learning control for batch process
HONG Yingdong, XIONG Zhihua, JIANG Yongheng, YE Hao
(Department of Automation, Tsinghua University, Beijing 100084, China)
To address problems of point-to-point tracking control for batch processes, three different initial errors of non-ideal initial states were analyzed and studied for convergence by 2 D Roesser model within the framework of tracking control algorithm. Conditions were provided to achieve zero or a neighborhood of zero tracking control errors between system and reference trajectory at various scenarios. For these unable to achieve zero tracking errors, boundaries of final tracking errors were given. Numerical simulation validated these convergence conditions and boundaries, and assessed effect of control parameters on these boundaries.
initial condition; iterative learning control; two-dimensional system theory; point-to-point tracking control
date:2017-01-22.
Prof. XIONG Zhihua, zhxiong@tsinghua.edu.cn
supported by the National Natural Science Foundation of China (61473162).
TP 13
A
0438—1157(2017)07—2826—07
10.11949/j.issn.0438-1157.20170106
2017-01-22收到初稿,2017-04-06收到修改稿。
联系人:熊智华。
洪英东(1990—),男,博士研究生。
国家自然科学基金项目(61473162)。

