桩基并联双螺旋型埋管换热器传热特性的数值仿真
朱税平,赵蕾,杨柳,王振宇
(1西安建筑科技大学环境与市政工程学院,陕西 西安 710055;2陕西省环境工程重点实验室,陕西 西安 710055;3西安建筑科技大学建筑学院,陕西 西安 710055;4同度可再生能源应用研究中心,江苏 昆山 215243)
桩基并联双螺旋型埋管换热器传热特性的数值仿真
朱税平1,2,赵蕾1,2,杨柳3,王振宇4
(1西安建筑科技大学环境与市政工程学院,陕西 西安 710055;2陕西省环境工程重点实验室,陕西 西安 710055;3西安建筑科技大学建筑学院,陕西 西安 710055;4同度可再生能源应用研究中心,江苏 昆山 215243)
摸清桩基并联双螺旋型埋管换热器的传热特性是进行合理设计、确保其高效运行的前提。建立了包含回水立管在内的桩基并联双螺旋型埋管换热器三维动态传热的仿真模型,利用其对现场实验的仿真复现及实心圆柱源热源模型解析解的对比验证了模拟结果的正确性。对桩身和土壤温度的模拟结果进行了分析,给出了沿管程、桩基内部以及周围土壤的温度分布。对连续和3种间歇运行模式下桩基并联双螺旋型埋管换热器的运行情况进行了仿真,揭示了其出口水温和单位管长放热量等性能参数的动态变化规律以及桩壁和周围土壤温度沿桩深和桩径方向的分布特征,提出了桩壁温度恢复百分比指标,定量评价了其在间歇运行模式下的温度恢复程度。表明了运停比越小,桩壁温度恢复程度越显著,但随着间歇运行周期的增加,每一间歇期的温度恢复程度呈现下降趋势。
计算流体力学;热传导;传热;桩基并联双螺旋型埋管换热器;实验验证;数值模拟;间歇运行
引 言
地源热泵系统因具有能耗低、换热性能好、环保等特点[1-3]而得到了迅速发展和应用。与传统的钻孔埋管换热器相比,桩基埋管换热器埋设于建筑物的混凝土桩基中,通过混凝土与周围土壤紧密接触,接触热阻更小,换热效率更高,可节省钻孔费用[4-5]。桩基埋管换热器有U型、W型、螺旋型埋管等形式[6-9]。在同一桩基内,螺旋型埋管比U型和W型埋管的换热面积更大,而且可减少管道连接的复杂性,有利于避免冷热支管温差所导致的两支管间的热交换,即热短路[10-11]。它作为一种全新的埋管换热器形式而受到关注。地埋管换热器设计是否合理决定着地埋管地源热泵空调系统的经济性和运行的可靠性[12-13]。例如 Cane等[14]指出实际工程中,由于缺乏可靠的设计方法和参数,北美地区地埋管换热器管长均比实际偏大10%~30%。目前,对桩基螺旋型埋管换热器的研究主要集中在传热模型上,如,刘俊红等[15-17]提出了“实心”圆柱源模型,方肇洪等[18-19]建立了考虑螺距影响的线圈热源模型,Man等[20]推导得出了使得模型更加接近实际情况的螺旋线热源模型。然而,上述解析解模型以定热流条件为前提,并忽略了回填料与土壤热物性的差别以及桩基中存在回水立管的影响。此外,部分学者对螺旋埋管通过数值解展开了研究。王蕊等[21]提出了二维轴对称传热模型,吴华剑[22]建立了桩基三螺旋埋管换热器数值模型,Zhang等[23-25]利用ANSYS CFX软件对单螺旋型埋管进行了三维数值模拟,Bezyan等[26]利用FLUENT软件对回水管绑扎在钢筋笼外部形式的桩基螺旋埋管换热器传热模型求解。总之,上述数值解模型中大多数因回水管的存在会使网格划分的难度增加、网格数量增大而被忽略,即使是包括回水管的桩基螺旋埋管研究中,也很少是工程实际中回水管绑扎在钢筋笼内部的形式。此外,根据热源叠加原理[27-28],桩基和土壤温度场对并联双螺旋埋管换热器的响应由各个单螺旋埋管内的水与混凝土、混凝土与土壤间的传热共同决定,其传热模型与桩基单螺旋型埋管换热器有明显的区别。这就导致对实际工程中应用的桩基并联双螺旋型埋管换热器传热模型研究的迫切需求。因此,本文针对桩基并联双螺旋型埋管换热器中的流动与三维传热问题建立了仿真数学模型,通过工程实测数据以及与实心圆柱源模型解析解的对比验证了数值解的可靠性之后,对桩身及周围土壤的温度分布及动态变化规律进行了分析;然后,结合建筑空调工程负荷特点,选定3种运停比,研究了各种间歇运行模式下桩基并联双螺旋型埋管换热器的传热性能以及沿桩深和半径方向不同位置处土壤温度的变化规律,采用温度恢复百分比为指标对桩基的温度恢复特性进行定量评价。
1 物理问题及数学模型
1.1 物理问题和控制方程组
桩基并联双螺旋型埋管换热器在土壤中的传热问题涉及管内水流与 PE管壁的对流换热以及桩基内钢筋混凝土和土壤中的导热过程。假定桩基内混凝土及土壤均为固体,其中的传热可视为纯导热[29]。管内的对流换热以及管外导热问题用连续性方程、动量方程和能量方程以及导热微分方程来描述,其通式统一描述可表示为[30]
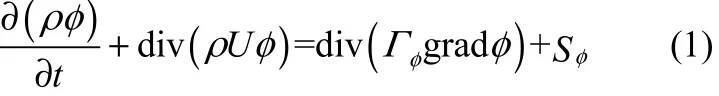
式中,ρ为水或固体的密度,kg·m-3;U 为水流速,m·s-1;φ为通用变量,可以代表u、v、w、T等未知变量;Sφ为广义源项;Γφ为广义扩散系数,m2·s-1。选用Realizable k-ε紊流模型对于管内的紊流换热进行求解。
1.2 几何模型以及网格划分
本研究的桩基并联双螺旋型埋管换热器,桩基深17 m,桩径为0.65 m;螺旋管埋深为16 m,每一根螺旋管螺距0.6 m、长62 m、管径25 mm,两根螺旋管交错盘旋;两进、回水管的中心间距分别为400和300 mm。选取半径3 m、高度20 m的圆柱体为计算区域,示意如图1所示。
利用 Gambit软件建立桩基及并联双螺旋埋管的几何模型,分别对螺旋管内、桩基内混凝土及桩外土壤区采用非结构化六面体/契形网格(Hex/Wedge)中cooper类型和非结构四面体网格(Tet Primitive)进行划分,采用Size function控制网格由密到疏变化,保证网格质量,网格结构如图2所示,网格数达482.4万。对控制方程离散化之后采用低 Reynolds数法进行管内紊流换热和管外导热问题的数值计算。
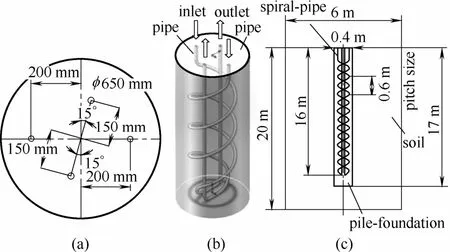
图1 数值仿真所涉及的桩基并联螺旋型埋管及其周围土壤计算区域的几何尺寸Fig.1 Simulation domain including double spiral pipes buried in parallel in pile-foundation with soil surrounding
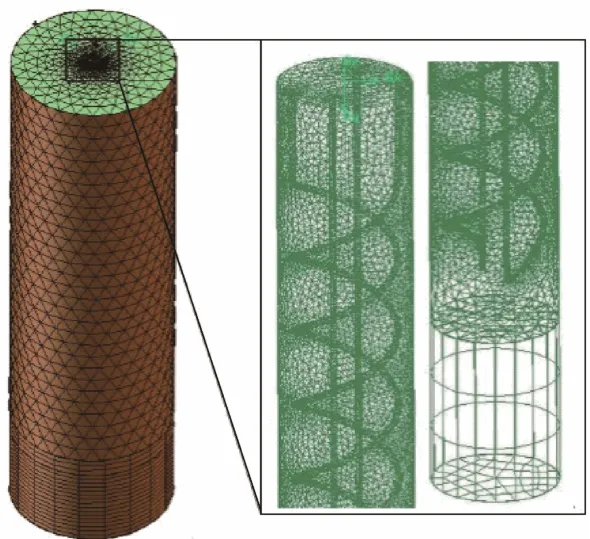
图2 3-D仿真区域及桩基内部网格划分情况Fig. 2 Grids generated in calculation domain
1.3 边界条件设置
三维数值仿真时边界条件设定情况见表1。
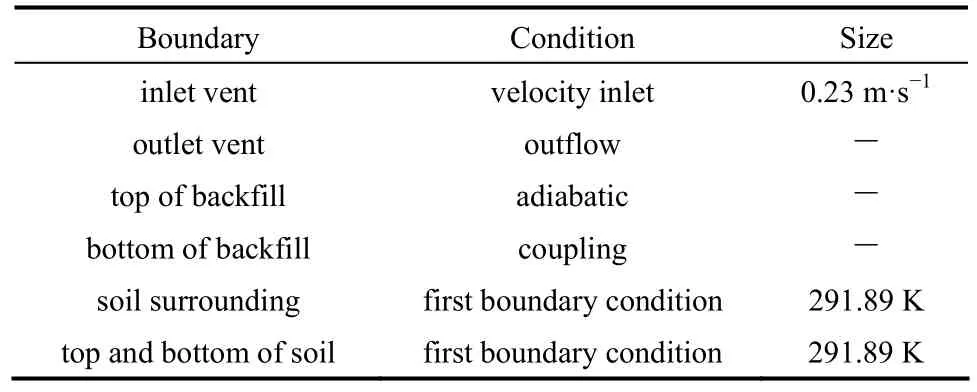
表1 边界条件的设定Table 1 Boundary conditions set for simulation
2 数值仿真结果验证
2.1 与实测结果的对比
为了验证数值解的准确性,对江苏某工程现场一17 m深的桩基并联双螺旋型埋管在冬季排热工况下连续运行20 h的传热实验进行了数值仿真。计算区域中各介质的相关物性参数依据现场实测值设定,见表 2。螺旋管进口的水流速度根据实测流量折算值设定,进口水温依照实测值的逐时拟合曲线来设定。土壤的初始温度依据实测数据设为 18.74℃。模拟结果与实测值对比如图3所示。
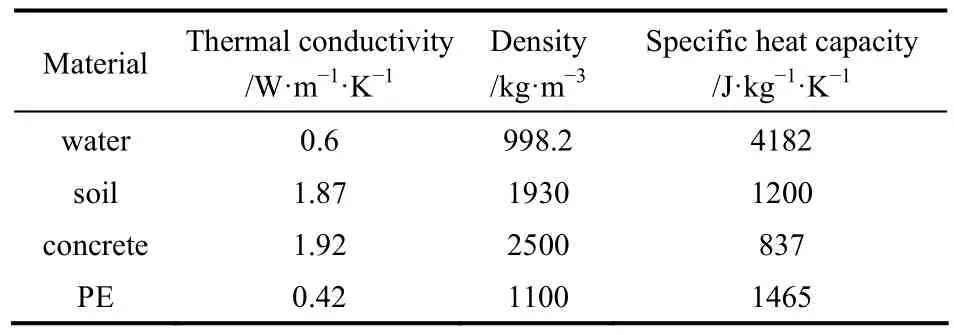
表2 计算区域中各物质的物性参数设定Table 2 Physical properties of materials within domain
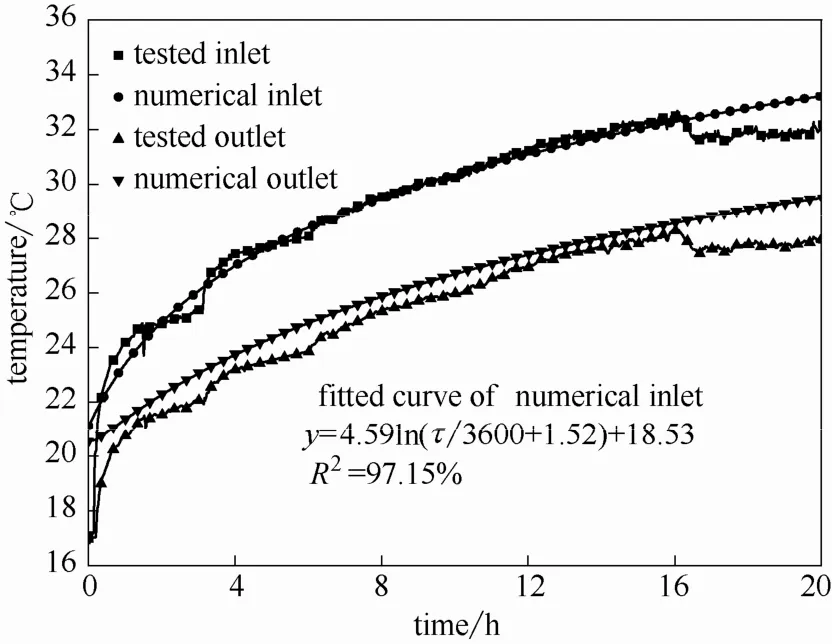
图3 出口水温实测值与模拟值的比较Fig.3 Comparison of measured and simulated inlet and outlet water temperature
图 3表明,进、出口水温差约为 3.7℃;最初0.5 h螺旋管出口水温模拟值与实测值的偏差是2.06℃,第16小时偏差仅为0.38℃,相对误差从11.1%降至1.4%;在第16.15小时之后,由于现场电压不稳定,实验被迫中止。但所获得的实验数据和模拟结果的对比可以表明该仿真模型解的可靠性。
2.2 与解析计算结果的对比
桩基断面尺寸通常远大于钻孔,桩体在地下换热器的传热过程中会产生不可忽视的影响,因而选用适合于桩基并联双螺旋型埋管换热器的实心圆柱热源模型及其解析解[11-13]对桩基埋管换热器的传热过程进行了求解,求解过程中的土壤热物性参数取值参照表2。选取第20小时时刻8 m深处水平截面的桩土温度的解析解与数值仿真解进行对比,如图4所示。
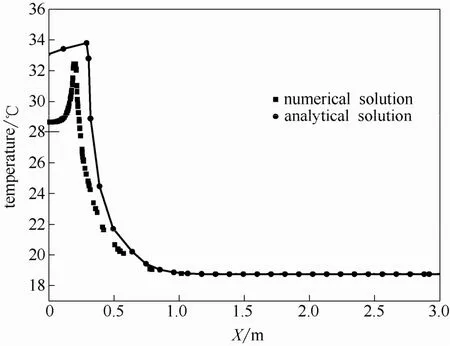
图4 桩土温度解析解与数值解的对比Fig.4 Comparison of analytical solution and numerical solution to pile soil temperature
图4表明,数值解与解析解在桩内偏差较大,例如X=0.1 m处相对误差达到14%,在X=0.5 m处相对误差已降到 5%以内,且在桩心、桩壁处温度的数值解较解析解小。这是因为桩土温度场的数值求解过程中,对桩内回填混凝土与土壤的热物性参数加以区分,且考虑了螺距及回水管的影响。距桩越远,土壤温度的数值解和解析解越接近,在大约X=0.8 m处之后土壤均维持在初始值温度。这表明,数值模型能更准确地揭示桩基内部螺旋埋管换热所引起的温度场的响应和分布。
3 模拟结果与分析
3.1 桩身的温度场分布
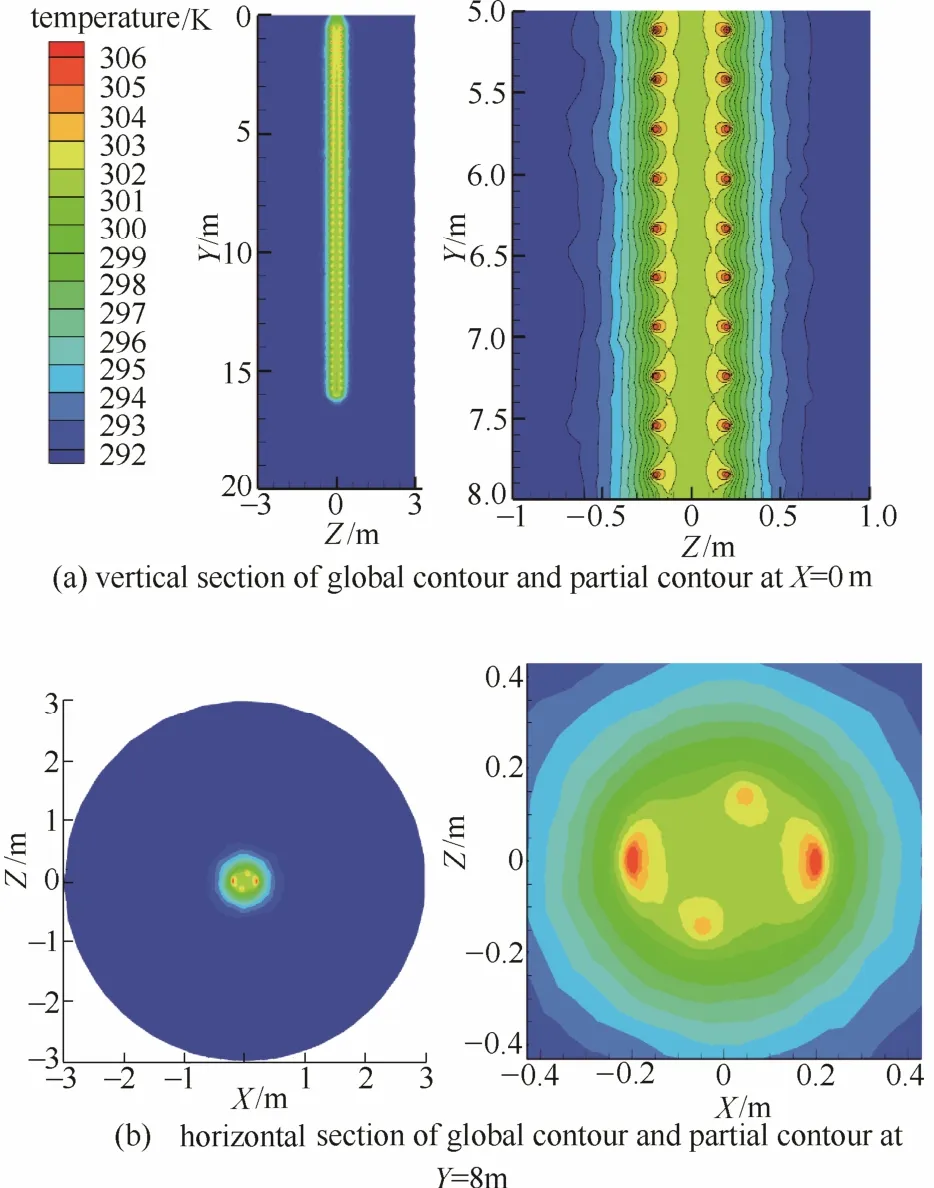
图5 第20小时桩基并联双螺旋型埋管计算区域内温度分布Fig.5 Simulated temperature distributions at 20th hour in domain with double spiral pipes in pile-foundation
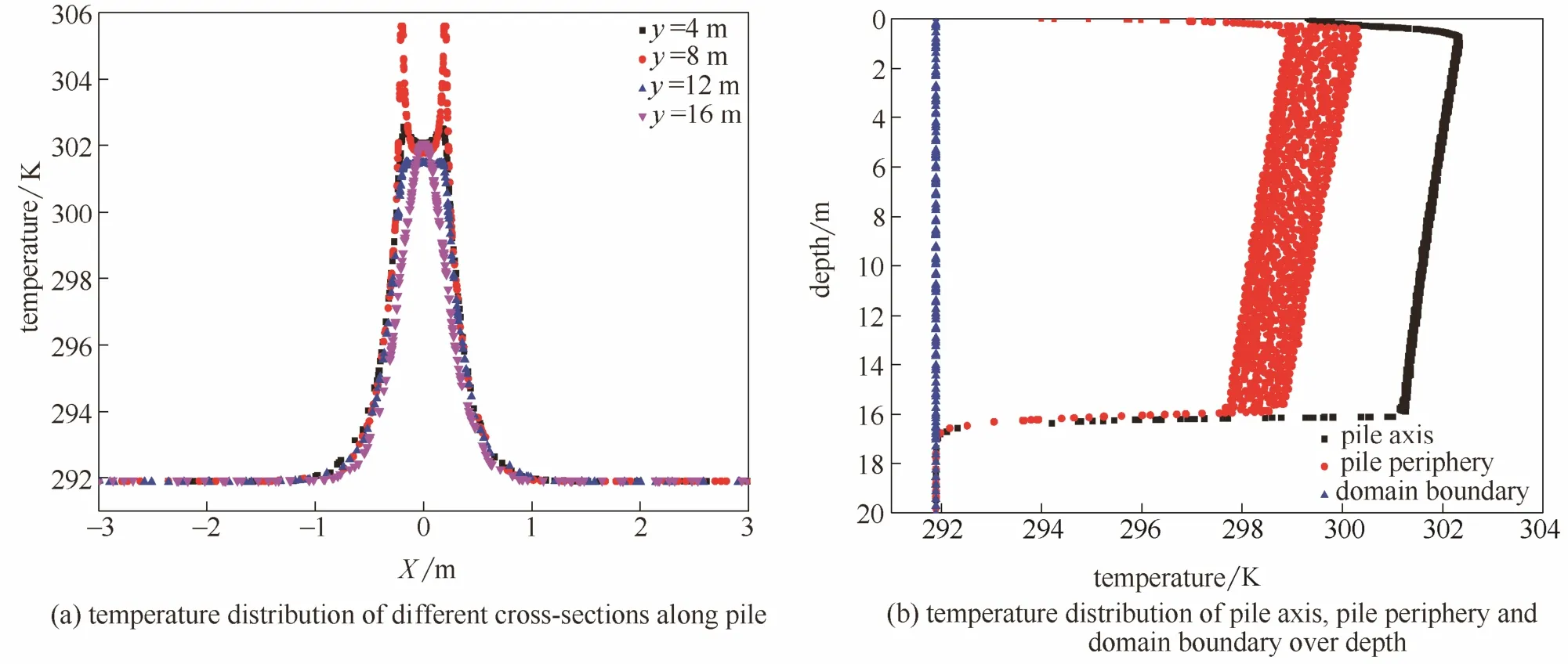
图6 第20小时计算区域内的不同深度的水平截面以及沿桩深方向桩心、桩周和计算区域外表面的温度分布Fig.6 Temperature distribution of different cross-sections along pile axis, pile periphery and domain boundary over depth at 20th hour
图5给出了第20小时时X=0 m及Y=8 m截面上温度的数值模拟结果。在系统排热工况下流体温度随着螺旋管长度的增加逐渐降低,入口温度高于出口温度。
模拟得到的第 20小时时刻沿不同桩深的水平截面上的温度分布以及桩心、桩周和土壤外表面温度沿桩深的分布如图6所示。由图可见,桩基内(水平方向-0.325~+0.325 m之间)在Y=4、8、12 m处桩心的温度最低,而在Y=16 m则相反(温度最高)。这是由于螺旋埋管内的水温沿着流动方向而降低[图5(a)],Y=16 m处为桩基并联双螺旋型埋管换热器底部,处在与混凝土接触的过渡面,因而温度随着与埋管距离的增加而降低,且桩基温度高于周围土壤温度。因为桩基体积有限,热容量有限,而土壤空间理论上可视为无限大,所以沿桩深方向土壤外壁的温度保持在291.89 K。在深度为1~16 m范围内桩心及桩壁温度沿桩深小幅度下降,在桩深17 m之后趋于定值291.89 K。沿桩深方向0~1、16~17 m内,桩心及桩壁温度变化显著,分别高达2.05、6.25℃以及 10.22、4.79℃,这是由流体与桩基及土壤之间的高温差所导致的。
3.2 沿管程的温度分布
为清楚地反映沿管程和回水立管的温度分布,对 X:Y:Z 取 1:16:1 缩放比例,第 20 小时时,沿管程的温度分布如图7所示。
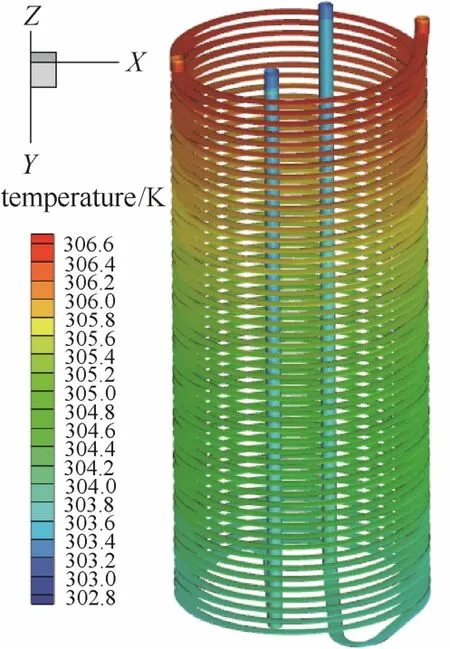
图7 第20小时沿管程和回水立管的温度分布Fig. 7 Temperature distributions along spiral pipes and the return riser at 20th hour
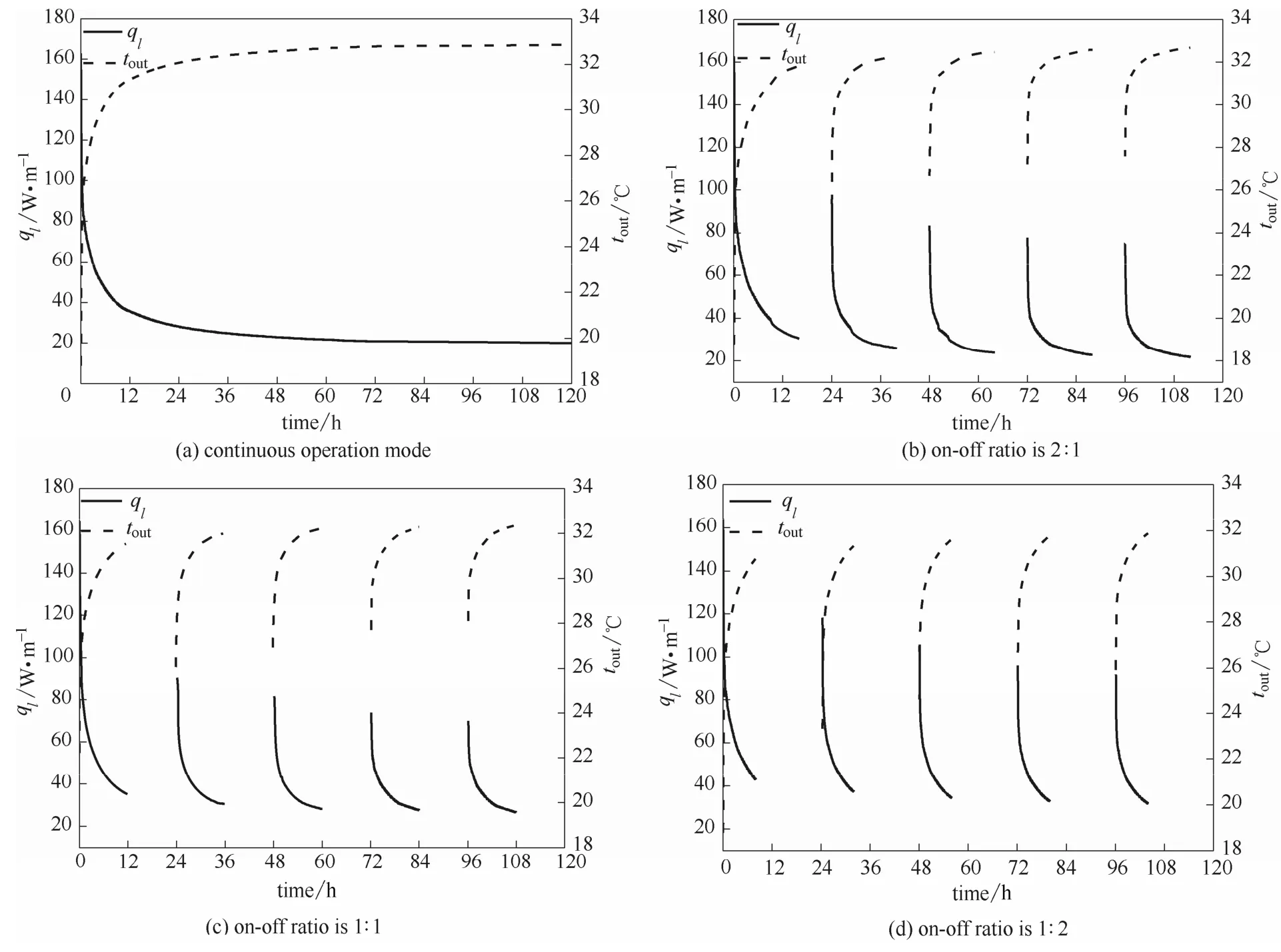
图8 连续和3间歇运行模式下5 d内单位管长换热量及出口水温的动态变化曲线Fig.8 Dynamic curves of qland toutin 5 d operations under continuous and three kinds of intermittent modes
虽然回水管位于相互交错盘旋的螺旋埋管内部,不可避免地受到周围埋管散热的影响,但回水管温度总体仍沿回流方向温度逐渐降低。回水立管的底部与顶部之间存在大约 0.5℃的温升,为流体进、出口总温变的 13.5%。可见,如忽略回水管的存在会造成一定的偏差。
4 间歇运行的传热与温度恢复特性
4.1 间歇运行模式的影响
为了考察桩基并联双螺旋型埋管换热器的间歇运行特性,取一天之中运停时间比分别为 2:1、1:1与1:2的间歇运行模式,对所模拟的桩基并联双螺旋型埋管换热器采用3种间歇模式和连续模式运行5 d的传热状况进行模拟,模拟时流体的进口温度及流速分别设为35℃和0.3 m·s-1,其他计算参数使用表1、表2的数据。
图8(a)~(d)给出了连续运行模式和3种间歇运行模式下单位管长换热量(即ql)和出口水温(tout)随时间的变化曲线。图8显示,连续运行模式下ql逐时下降,下降幅度逐渐减小;3种间歇运行模式下,ql总体趋势也是逐时下降,但每次间歇后,ql比上一运行期结束时有明显提高,但仍比其最初运行时低。这是因为土壤的温度虽然得到了一定程度的恢复,但并未恢复到初始温度。运行 1周后,4种运行模式所对应的ql分别为20.01、21.85、26.62和31.73 W·m-1,3种间歇模式下ql分别比连续运行模式下高 9.2%、33.03%和58.57%。连续运行模式下tout逐时上升,上升幅度逐渐减小,32 h之后基本趋于稳定;3种间歇运行模式下,tout总体趋势也是逐时逐渐上升,但每次间歇后,tout比上个运行期结束时有明显下降,但仍比其最初开始时出口水温高。运行1周后,4种运行模式所对应的tout分别为32.88、32.69、32.37和31.86℃。
4.2 沿桩深方向桩壁温度的动态变化规律
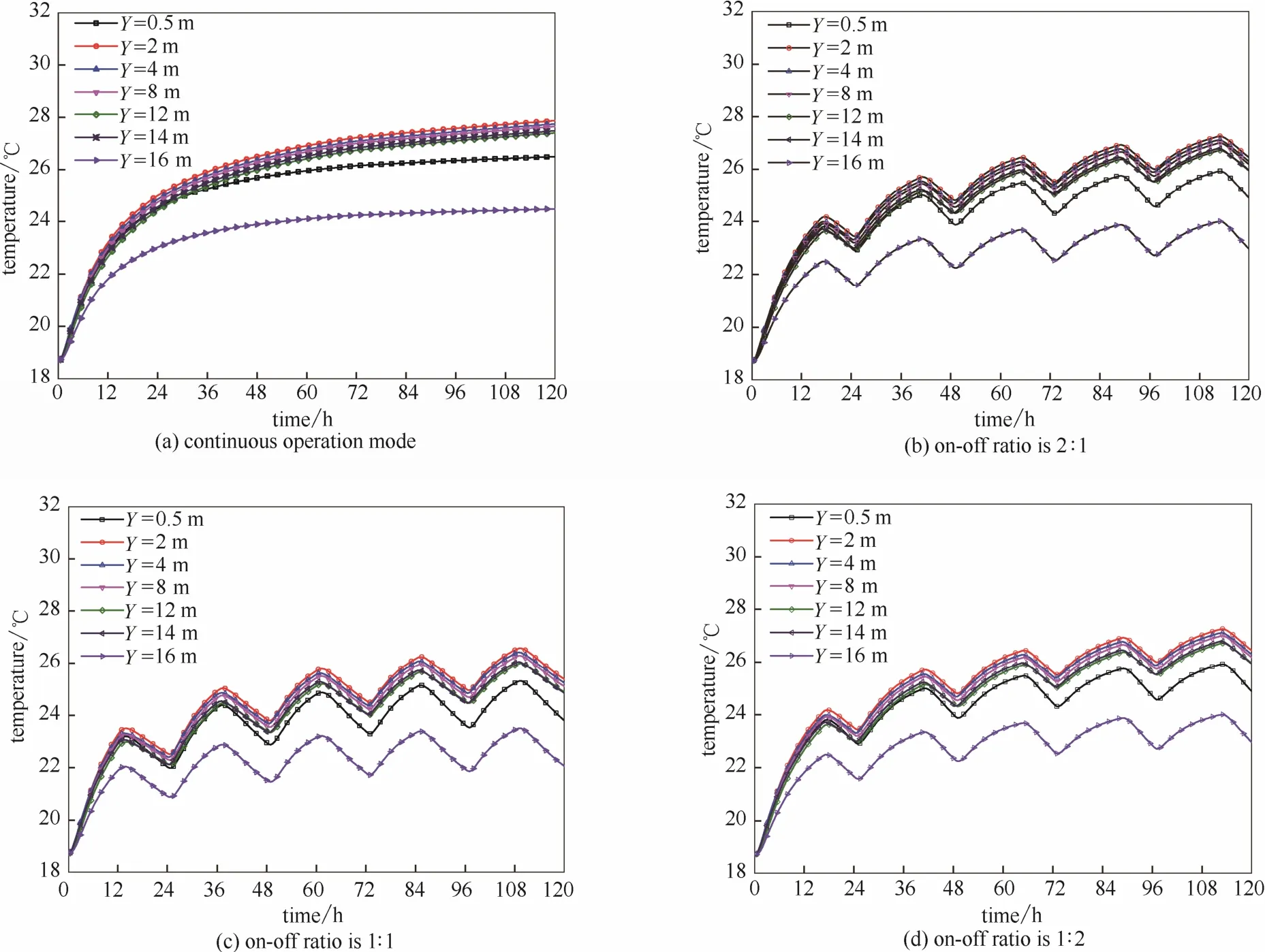
图9 连续和3种间歇运行模式下沿桩深方向不同位置处桩壁的温度动态变化曲线Fig.9 Dynamic curves of temperature along pile periphery at different depths under continuous and 3 kinds of intermittent operational modes
图9给出了连续和3种间歇运行模式下沿桩深不同位置处的桩壁动态温度曲线。深度为0.5、16 m处桩壁的温度明显不同于2~14 m各深度处的桩壁温度。这是由于0.5、16 m处桩壁温度受土壤顶面及底面传热的影响较大的缘故;而深度为2~14 m之间的桩壁温度主要由埋管的散热强度决定。
定义深度为2~14 m之间桩壁温度平均值为桩壁的平均温度,在连续运行5 d后,桩壁温度上升最显著,平均温度最高达到27.53℃,比土壤原始温度升高8.79℃。这是因为连续运行埋管的换热量最大。在3种不同间歇运行模式下桩壁温度呈波浪状上升,共出现5次峰值和5次谷值。运停时间比分别为 2:1、1:1 与 1:2 的情况下,5 d 之后桩壁的平均温度最高分别达到了26.16、25.08和23.81℃,温升分别为7.42、6.34和5.06℃。这表明桩基周围土壤温度变化与桩基埋管的停运比紧密相关,运行时间越长,温度变化越大;停止运行期间,桩壁的平均温度缓慢下降,得到一定程度的恢复。
4.3 沿径向土壤温度的时空分布规律
图10给出了不同运行模式下8 m深处温度沿径向的动态变化曲线,r表示与桩基轴心的距离。可见,在连续运行模式下,各位置处的温度均呈单调上升趋势,不同测点的上升幅度不同,但上升幅度均逐时减小。在120 h时刻,r为0.25~3 m的各监测点温度由近及远依次地升高了 12.12、8.91、6.46、3.92、1.75、1.07、0.72、0.13及 0.004℃。这是因为离螺旋埋管越近,温度升高越快,且幅度越大。因混凝土的热导率大于土壤的,故在桩内外测点的温升幅度相差较大。在3种间歇运行模式下,桩内、桩壁及土壤沿径向的的温度均呈波动上升趋势。其中,对于r>0.75 m的各点处的温度波幅几乎不因间歇运行模式不同而异。在间歇期间,由于埋管向土壤释放的热量逐渐减小以至为 0,所以土壤温度在间歇期内下降,得到一定程度的恢复。经过一周运行后,r=0.75 m处连续运行模式、运停比分别为 2:1、1:1与 1:2的 3种间歇运行模式所对应温度分别为 22.65、22.21、21.82和21.25℃。
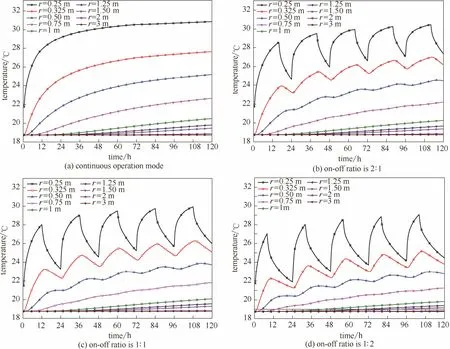
图10 连续和3种间歇运行模式下Y=8 m处沿径向不同位置处的温度动态变化曲线Fig.10 Dynamic curves of temperature along radius on Y=8 m under various modes under continuous and 3 kinds of intermittent operation mode
4.4 桩壁温度的恢复特性
在桩基埋管换热器间歇运行模式中,桩壁温度恢复的快慢及其程度对交替运行时桩基埋管换热器的换热性能起着重要的作用。因此,分别定义桩壁温度变化速度ζ1和桩壁温度恢复百分比ζ2来反映桩壁温度的恢复快慢和程度。
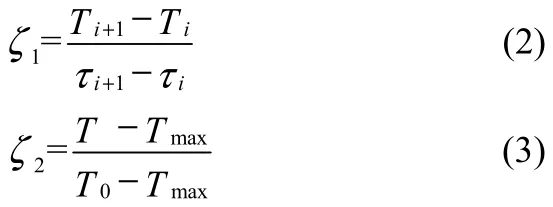
式中,Ti+1、Ti分别为埋管间歇第i+1和第i时刻桩壁的平均温度;τi+1、τi分别为埋管间歇第i+1和第i时刻;T0为土壤的原始温度;Tmax为某间歇阶段桩壁温度的最大值,T为 Tmax之后任意时刻的温度。
运停比为1:1的情况下,桩壁温度变化速度和恢复百分比分别如图11(a)、(b)所示。图11(a)显示,桩壁温度在最初停止运行的1~2 h内仍呈上升趋势,且上升速度逐渐减小。这是由于埋管换热器中滞留的水温35℃远高于土壤的温度,且土壤存在一定的蓄热能力。但是,桩壁温度大约上升0.3℃后才开始下降,且最初下降速度较快而后逐渐变缓并趋于稳定。图11(b)显示,间歇时段内桩壁温度的恢复百分比与时间呈正比,而随着天数的增加,温度恢复百分比逐渐降低。比如,运停比为1:1时第1天的桩壁温度恢复百分比为21.4%,而第3天已降为18.53%。
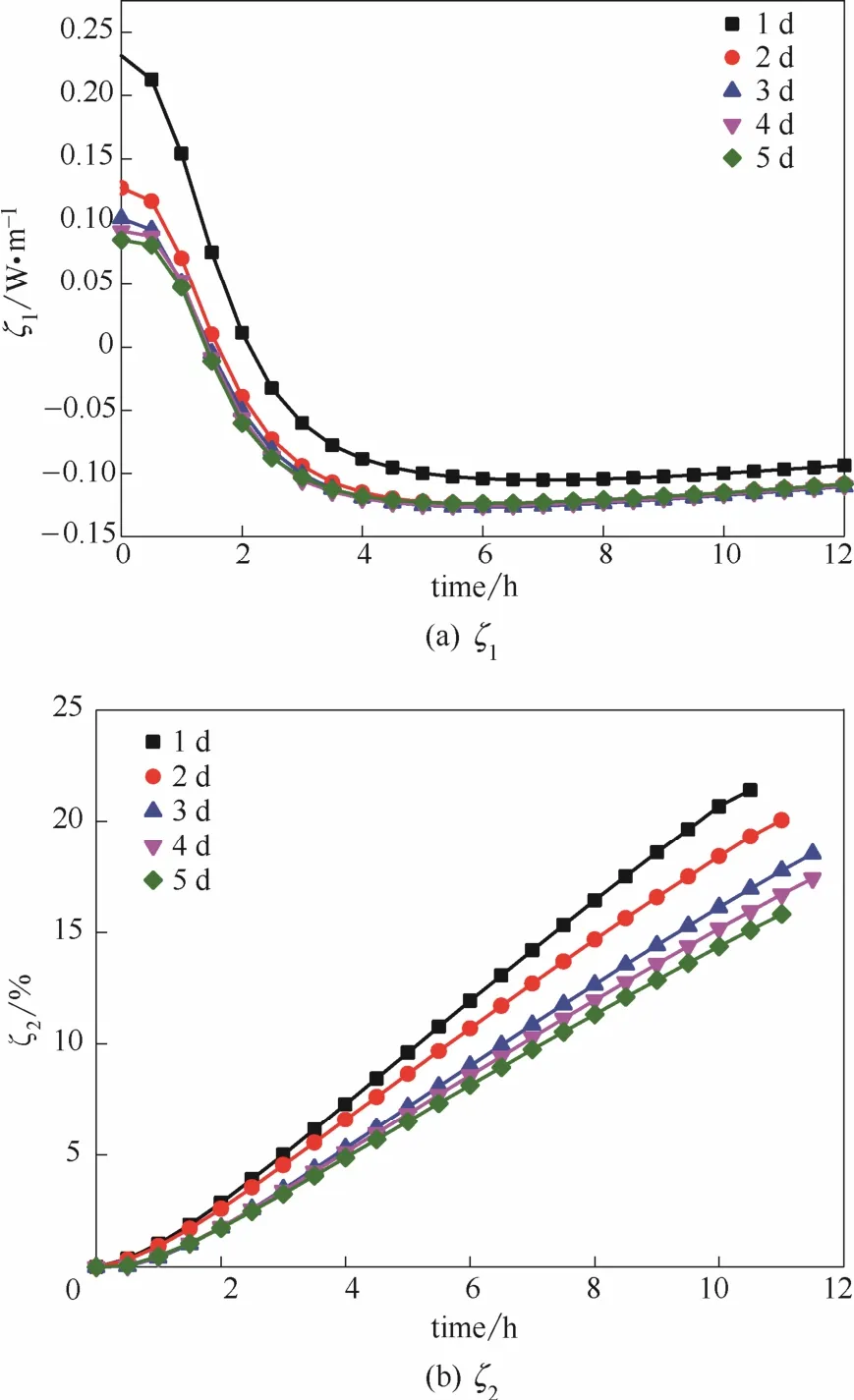
图11 运停比1:1的间歇模式下桩壁温度的ζ1和ζ2动态变化曲线Fig.11 Dynamic curves of ζ1and ζ2at pile wall under 1:1 intermittent mode
5 结 论
建立了包含回水立管在内的桩基并联双螺旋型埋管换热器传热问题的三维动态仿真模型,利用对现场实验的数值仿真复现验证了模拟结果的正确性。排热工况下的数值仿真结果表明了沿桩深方向0~1及16~17 m内,桩心及桩壁温度变化明显,土壤表面及底面的温度对近端桩壁温度的影响不可忽略,而在2~16 m范围内,其温度沿桩深方向逐渐降低,主要受桩基散热强度的影响。混凝土和土壤热导率的差异导致同一深度处桩内、外各测点的温升幅度相差较大,且随与螺旋埋管的距离增大而减小。
无论连续还是间歇运行模式下,单位管长换热量总体均呈逐渐下降趋势,下降的幅度逐渐减小,但间歇运行模式下,土壤和桩基的温度在每次间歇后得到了一定程度的恢复,换热量也有所回升。在埋管停止运行的最初1~2 h内,桩壁温度仍会上升,但上升速度减小,桩壁温度大约上升0.3℃达到最大值后才开始下降。在每一个间歇周期内,桩壁温度恢复百分比与间歇时间呈正比,随着天数的增加,温度恢复百分比逐渐降低。
[1] SARBU I, SEBARCHIEVICI C. General review of ground -source heat pump systems for heating and cooling of buildings[J]. Energy &Buildings, 2014, 70(1): 441-454.
[2] SELF S, REDDY B, ROSEN M. Geothermal heat pump systems:status review and comparison with other heating options[J]. Applied Energy, 2013, 101(1): 341-348.
[3] FAIZAL M, BOUAZZA A, SINGH R M. Heat transfer enhancement of geothermal energy piles[J]. Renewable and Sustainable Energy Reviews, 2016, 57: 16-33.
[4] BRANDL H. Energy foundations and other thermo-active ground structures[J]. Geotechnique, 2006, 56(2): 81-122.
[5] 桂树强, 程晓辉, 张志鹏. 地源热泵桩基与钻孔埋管换热器换热性能比较[J]. 土木建筑与环境工程, 2013, 35(3): 151-156.GUI S Q, CHENG X H, ZHANG Z P. Comparative analysis of heatexchange performance of energy piles and borehole heat exchangers in GSHP system[J]. Journal of Civil, Architectural & Environmental Engineering, 2013, 35(3): 151-156.
[6] CECINATO F, LOVERIDGE F A. Influences on the thermal efficiency of energy piles energy[J]. Energy and Buildings, 2015, 82:1021-1033.
[7] ZHAO Q, CHEN B M, LIU F. Study on the thermal performance of several types of energy pile ground heat exchangers: U-shaped, W-shaped and spiral-shaped[J]. Energy and Buildings, 2016, 133: 335-344.
[8] ZARRELLA A, CARLI M D, GALGARO A. Thermal performance of two types of energy foundation pile: helical pipe and triple U-tube[J]. Applied Thermal Engineering, 2013, 61(2): 301-310.
[9] PARK S, LEE D, CHOI H J, et al. Relative constructability and thermal performance of cast-in-place concrete energy pile: coil-type GHEX (ground heat exchanger)[J]. Energy, 2015, 81: 56-66.
[10] CUI P, LI X, MAN Y, et al. Heat transfer analysis of pile geothermal heat exchangers with spiral coils[J]. Apply Energy, 2011, 88(11):4113-4119.
[11] 茅靳丰, 李永, 张华, 等. 地埋管换热器热短路及其对热物性测试影响分析[J]. 化工学报, 2013, 64(11): 4015-4024.MAO J F, LI Y, ZHANG H, et al. Thermal short-circuiting and its influence on thermal response in borehole heat exchangers[J]. CIESC Journal, 2013, 64(11): 4015-4024.
[12] 陈超, 王永菲, 任艳, 等. 竖直U形地埋管换热器传热热阻计算方法比较[J]. 湖南大学学报(自然科学版), 2009, 36(12): 58-62.CHEN C, WANG Y F, REN Y, et al. Comparison of vertical U-tube ground heat exchanger thermal resistance calculation methods[J].Journal of Hunan University (Natural Sciences), 2009, 36(12): 58-62.
[13] SELAMAT S, MIYARA A, KARIYA K. Numerical study of horizontal ground heat exchangers for design optimization[J].Renewable Energy, 2016, 95: 561-573.
[14] CANE R L D, FORGAS D A. Modeling of GSHP performance[J].ASHRAE Trans., 1991, 97(1): 909-925.
[15] 刘俊红, 张文克, 方肇洪. 桩埋螺旋管式地热换热器的传热模型[J]. 山东建筑大学学报, 2010, 25(2): 95-100.LIU J H, ZHANG W K, FANG Z H. Solid cylindrical heat source model for pile ground heat exchangers with spiral coils[J]. Journal of Shandong Jianzhu University, 2010, 25(2): 95-100.
[16] 石磊, 张方方, 林芸, 等. 桩基螺旋埋管换热器的二维温度场分析[J]. 山东建筑大学学报, 2010, 25(2): 177-183.SHI L, ZHANG F F, LIN Y, et al. The 2-D thermal analysis of the coil ground heat exchanger inside piles[J]. Journal of Shandong Jianzhu University, 2010, 25(2): 177-183.
[17] DIAO N R, CUI P, LIU J H, et a1. R&D of the ground-coupled heat pump technology in China[J]. Frontiers of Energy and Power Engineering in China, 2010, 4(1): 47-54.
[18] ZHANG W K, YANG H X, LU L, et al. Investigation on heat transfer around buried coils of pile foundation heat exchangers for ground-coupled heat pump applications[J]. International Journal of Heat and Mass Transfer, 2012, 55(21/22): 6023-6031
[19] 李新, 方亮, 赵强, 等. 螺旋埋管地热换热器的线圈热源模型及其解析解[J]. 热能动力工程, 2011, 26(4): 476-479.LI X, FANG L, ZHAO Q, et al. The 2-D thermal analysis of the coil ground heat exchanger inside piles[J]. Journal of Engineering for Thermal Energy and Power, 2011, 26(4): 476-479.
[20] MAN Y, YANG H X, DIAO N R, et al. Development of spiral heat source model for novel pile ground heat exchangers[J]. HVAC & R Research, 2011, 17(6): 1075-1088.
[21] 王蕊, 赵静野, 陈晓春. 桩埋螺旋管地热换热器的数值模拟[J]. 北京建筑工程学院学报, 2013, 29(1): 25-29.WANG R, ZHAO J Y, CHEN X C. Numerical simulation for pile ground heat exchangers with spiral coils[J]. Journal of Beijing University of Civil Engineering and Architecture, 2013, 29(1): 25-29.
[22] 吴华剑. 桩基螺旋埋管换热器性能研究[D]. 重庆: 重庆大学,2012.WU H J. Study on performance of pile spiral pipe heat exchanger[D].Chongqing: Chongqing University, 2012.
[23] WANG D Q, LU L, ZHANG W K, et al. Numerical and analytical analysis of groundwater influence on the pile geothermal heat exchanger with cast-in spiral coils[J]. Applied Energy, 2015, 160:705-714.
[24] ZHANG W K, YANG H X, LU L, et al. The research on ring-coil heat transfer models of pile foundation ground heat exchangers in the case of groundwater seepage[J]. Energy and Buildings, 2014, 71:115-128.
[25] ZHANG W K, YANG H X, LU L, et al. The analysis on solid cylindrical heat source model of foundation pile ground heat exchangers with groundwater flow[J]. Energy, 2013, 55: 417-425.
[26] BEZYAN B, PORKHIAl S, MEHRIZI A A. 3-D simulation of heat transfer rate in geothermal pile-foundation heat exchangers with spiral pipe configuration[J]. Applied Thermal Engineering, 2015, 87:655-668.
[27] FANG Z H, DIAO N N, CUI P. Discontinuous operation of geothermal heat exchangers[J]. Tsinghua Science and Technology,2002, 7(2): 194-197.
[28] 杨卫波, 施明恒. 基于线热源理论的垂直 U型埋管换热器传热模型的研究[J]. 太阳能学报, 2007, 28(5): 482-488.YANG W B, SHI M H. Study on heat transfer model of vertical U-tube ground heat exchangers based on line heat source theory[J].Acta Energiae Solaris Sinica, 2007, 28(5): 482-488.
[29] PIECHOWSKI M. Heat and mass transfer model of a ground heat exchanger: validation and sensitivity analysis[J]. Int. J. Energy Res.,1998, 22(11): 965-979.
[30] 陶文铨. 数值传热学[M]. 2版. 西安: 西安交通大学出版社, 2001: 5.TAO W Q. Numerical Heat Transfer[M]. 2nd ed. Xi’an: Xi’an Jiaotong University Press, 2001: 5.
Numerical studies on heat transfer characteristics of pile heat exchanger with double spiral pipes buried in parallel
ZHU Shuiping1,2, ZHAO Lei1,2, YANG Liu3, WANG Zhenyu4
(1School of Environmental and Municipal Engineering, Xi’an University of Architecture and Technology, Xi’an 710055,Shaanxi, China;2Key Laboratory of Environmental Engineering, Xi’an 710055, Shaanxi, China;3School of Architecture, Xi’an University of Architecture and Technology, Xi’an 710055, Shaanxi, China;4Tong Du Renewable Energy Application Research Center, Kunshan 215243, Jiangsu, China)
It is critical to understand the heat transfer characteristics of pile heat exchanger (PHE) with double spiral pipes buried in parallel so that it can be designed feasibly and operated efficiently. Therefore, a 3-D dynamic simulation model as established to study the heat transfer processes of a pile heat exchanger in which double spiral pipes and the return risers were buried in parallel. And the numerical simulation results were validated by the data obtained in an in-situ test and analytical solution of the solid cylindrical heat source model. The temperature distributions along the pipes, in the pile body and soil surrounding are illustrated and analyzed. A continuous and three intermittent heat transfer processes of this PHE were simulated dynamically. Such parameters as the dynamic outlet water temperatures of the buried parallel double spiral pipes and the heat transfer rate per unit pipe length are revealed. The temperature variations at different locations on the pile wall and in the soil surrounding along the pile depth and in radial directions are analyzed. The index of pile wall temperature recovery percentage isproposed to quantify the temperature recovery degree under different intermittent operational modes. It is found that the smaller the on-off ratio, the more significantly the temperature recovery degree along the pile wall can be achieved. But the recovery degree in each intermittent period tends to decrease as the operational cyclic increases.
computational fluid dynamics; heat conduction; heat transfer; pile heat exchanger with double spiral pipes buried in parallel; experimental validation; numerical simulation; intermittent mode
date:2016-12-12.
Prof. ZHAO Lei, leizhao0308@ hotmail.com
supported by the National Key Technology Research and Development Program of China (2014BAJ01B01).
TK 521
A
0438—1157(2017)07—2730—09
10.11949/j.issn.0438-1157.20161741
2016-12-12收到初稿,2017-04-06收到修改稿。
联系人:赵蕾。
朱税平(1991—),女,硕士研究生。
国家科技支撑计划项目(2014BAJ01B01)。

