静电场作用下电介质系统的平衡态及其稳定性
韩光泽,马乐晗
(华南理工大学物理系,广东 广州 510641)
静电场作用下电介质系统的平衡态及其稳定性
韩光泽,马乐晗
(华南理工大学物理系,广东 广州 510641)
热力学平衡态是系统能量最低状态,在没有外界作用的条件下任何非平衡态最终都会趋向平衡态,热力学系统只有在平衡态才能用统一的状态参量来描述。电磁场能够有效地强化传热传质过程,对电介质系统的平衡及其稳定性有明显的作用。利用热力学定律将电场能量引入热力学基本微分式,构建了电场作用下电介质系统的熵函数,利用平衡态及其稳定性的熵判据导出了静电场作用下电介质系统的平衡条件及稳定条件。相比没有电场作用,平衡条件要求系统各相的等效压强、等效化学势和平行极板间电场强度相等;稳定条件要求产生电场的电荷量与电势呈正比。电场作用下的等效压强包括了电场极化作用的力学效果,力学平衡由压强和电极化力共同决定;等效化学势包括了电场极化势能的效果,相平衡由浓度和电势能共同决定。热力学结论与电动力学及统计物理的结论一致,已被实验证实。
热力学;熵;相平衡;汽液平衡;稳定性
引 言
热力学平衡态是热力学体系具有状态函数的理论基础,是指在没有外界影响的条件下,系统各部分的性质长时间内不发生变化的状态[1]。任何非平衡态在没有外界做功或传热的条件下经过一定的时间最终都会趋向平衡态;孤立系统无论其初始状态如何复杂,最终也一定会达到平衡状态。当系统处于不平衡的状态时,系统内部各部分的状态参量互不相同,无法用统一的状态参量来描述整个系统;只有当系统处于平衡状态时,各种宏观物理量才具有确定的值。热力学系统的平衡态是其能量最低的状态,利用平衡状态参量的数据可以判断一个给定系统有多大的利用价值[2]。当热力学系统与外界环境或系统各部分达到平衡时,系统的宏观热力学参量一定满足特定的热力学方程,这就是系统的平衡条件。由于自发的热扰动造成的涨落或者是外界的干扰,系统的状态可能出现暂时的、微小的偏离平衡态的现象,如果系统能够依靠自身的特性恢复到原来的状态,就是稳定平衡态[3]。稳定性不仅是指处于一定条件下的系统具有不发生变化的能力,更主要的是指系统所具有的抗干扰能力。稳定性给予了热力学函数的变化以一定限制。系统稳定性的含义不仅可以用于宏观热力学,还可以推广到化学平衡、生态系统、动力学等各个方面[4]。
热力学平衡判据是用来判断系统是否达到平衡态的热力学函数,是通过热力学第一定律和第二定律从宏观上揭示平衡态存在的根源,并确定对各种约束类型系统所应使用的形式以及确定平衡条件和稳定条件的准则,具有普遍适用性。经典热力学研究的是处于平衡态的系统[5],判断一个系统是否处于平衡状态对于研究一个具体的实际系统具有非常重要的意义。只有知道了平衡条件和平衡稳定条件,才能研究物质系统的热力学性质;系统的相图、临界态和化学反应方向等都是通过平衡条件和平衡稳定条件得到的。将系统所处的实际约束条件与相应的平衡及稳定条件比较,可以判断相应热力学过程是否存在以及是否有实际价值[6-8]。因此,热力学平衡判据是研究平衡态热力学的先决条件。
电磁场技术已经发展成为一门覆盖领域广泛、应用方式多样的综合性技术,例如,利用电场强化传热传质过程[9-16]、利用电热效应制冷[17-18]等已有诸多的文献报道。这些文献大多是关于电场作用下电介质系统的某些热力学特征的实验研究或理论研究,关于在电场作用下电介质系统平衡态及其稳定性问题还未见文献报道。电场与电介质的相互作用对热力学系统的平衡态及其稳定性必定有影响,系统的平衡条件及稳定条件因电场的作用也会发生变化。因此有必要研究电场作用下热力学系统的平衡及其稳定性质。经典热力学具有普遍适用性,热力学基本方程适用于所有热力学系统,包括电场作用下的电介质热力学系统[19]。本文从热力学的基本原理出发,结合电磁学理论和电介质理论,导出电场作用下热力学系统的平衡判据,并由此研究电介质热力学系统的平衡条件及稳定条件。
1 平衡态及其稳定性的熵判据
1855年德国物理学家和数学家克劳休斯在研究热机循环的过程中引进了熵的概念,并提出了具有普遍意义的克劳休斯不等式[1-2]

式(1)也被认为是热力学第二定律的数学表述,其中等号对应于可逆过程,大于号对应于不可逆过程。孤立系统与外界既没有能量交换也没有物质交换,Q=0;孤立系统中发生的任何过程都是自发的,而自然界的任何自发过程都是不可逆的。因此对孤立系统有[20]

式(2)表明,孤立系统中的任何过程只能沿熵增加的方向进行,这就是熵增加原理。当系统达到平衡状态,不再发生变化时,系统的熵达到最大值,即孤立系统的平衡态对应熵取最大值的状态。设孤立系统的熵是S(x1,…,xn),将熵变在极值点做泰勒展开[1]

因此,孤立系统的熵取极大值的充要条件是

由δS=0可以确定熵的极值点,因此它决定了平衡态的必要条件;由δ2S<0可以确定极大值,因此这就是系统平衡态的稳定条件。如果在约束条件下,系统的熵对于各种可能的变动有若干个极大值,则其中最大的对应稳定平衡,其他对应亚稳平衡。熵判据只适用于孤立系统,但实际的系统都不是孤立的。通常做法是将与所研究的系统有相互作用的所有外界都包括在一起,构成一个扩大的孤立系统。
2 电场作用下电介质系统的熵函数
设在某一微小过程中,系统从外界吸收了热量δQ,同时外界对系统做的各种形式的功是∑δW,则热力学第一定律可以普遍地表示为 dU=δQ+∑δW。由于做功是能量的传递与转换过程,该式也可理解为系统热力学能(内能)的变化等于系统所包含的各种形式能量变化的和[21-22]。除传热外,系统可以通过多种形式的功与外界交换能量。当有电场作用于多组分热力学系统,系统热力学能的微分可以普遍地表示为[23-24]

设有如图1所示的孤立系统,两块面积为A、相距为L、相互平行放置的带电量为q金属板产生匀强电场,由两相(α相和β相)组成的电介质系统位于金属极板间。金属板表面附近的电位移等于电荷面密度 D=σ=q/A,极板间电介质系统的体积是V=AL,则系统的电场能量可以表示为[25]We=(D2/2ε0ε)V=(L2/2ε0)(q2/εV),对于多组分系统 ε是各组分介电常数的摩尔平均值。当系统发生相变时,各相的极板面积和电荷量发生变化,极板间距不变。通常情况下可忽略电场强度对介电常数的影响[25],介电常数的微分可以表示为dε=ερdρ=∑Μi(ερ/V)dni-(ρερ/V)dV,该电场能量的变化可以表示为
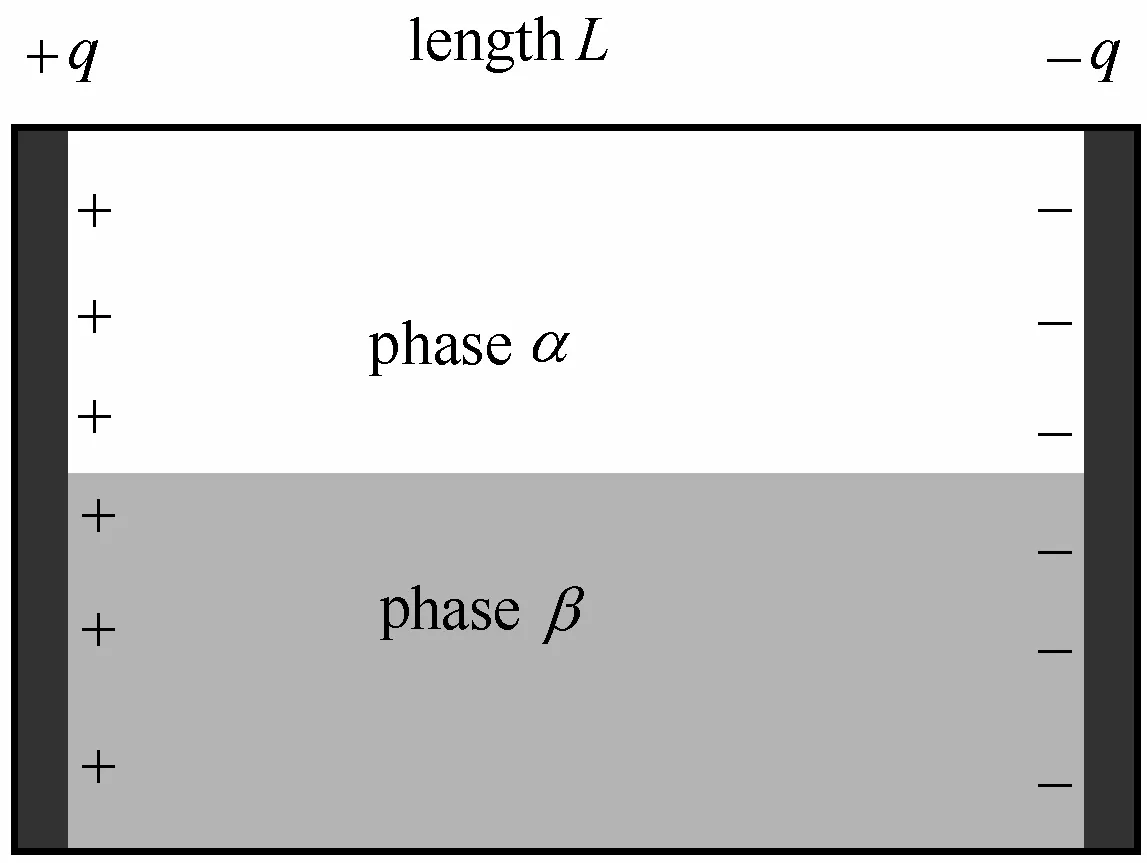
图1 电场中的两相系统Fig. 1 Two-phase system in electric field

将式(6)代入式(5)得

令式(7)中自变量的系数

则可以由式(7)将该电介质系统的熵函数表示为

这个熵函数表达式同样具有普遍性,既可用于整个系统,又可用于系统中的每一相。
3 静电场作用下电介质系统的平衡条件和稳定条件
3.1 平衡条件
对于图1所示的电介质系统,每一相的热力学能、体积、物质的量和电荷量可以独立变化,但整个系统的总量不变,即该孤立系统的约束条件为

将熵微分式(9)分别应用到系统的α相和β相,并利用约束条件式(10)得整个系统的熵变化

由于该微分式右侧的自变量都是独立变量,因此如果系统的熵变化要满足平衡条件式(4),式(11)中的每一项都必须等于零

这就是电场作用下电介质系统的平衡条件。
3.2 平衡稳定条件
对熵的一阶微分式(9)再做一次变分得系统熵的二阶变分


极板所带的电荷量与系统的温度和压强无关,即(∂q/∂T)p′,n,ζ=(∂q/∂p′)T,n,ζ=0。将这 4 个微分式以及代入熵的二阶变分式(13)整理得

由于式(15)中的δT、δp′、δn 和δζ都是独立变量,因此为了满足稳定条件式(4)δ2S<0,式(15)中的每一项都应该小于零,即
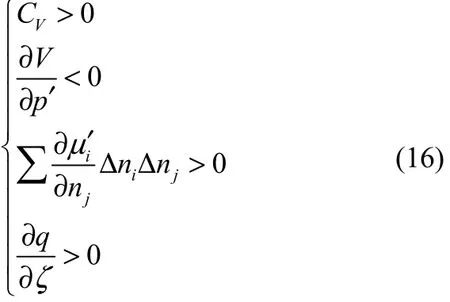
这就是电场作用下电介质系统的稳定条件。
3.3 平衡条件及稳定条件的要求
电介质系统的平衡条件式(12)中 Tα=Tβ、p′α=p′β和μι′α=μι′β分别是热、力学和相变平衡条件;而第 4项ζα=ζβ是电场作用所必须满足的平衡条件,可称为电平衡条件。将关系式D=ε0εE代入定义式(8)可得ζ=EL,因此ζ就是两极板间的电压。该条件要求两极板间的电压在两相的部分必须相等。这个条件自然可以得到满足,因为金属极板是一个等势体,同一块极板分别位于两相中的部分的电势必定相等。由于需要满足经典热力学中的均匀性要求,两块金属极板平行放置,因此两相间的电势相等也等价于两相的电场强度相等。虽然两相的电势和场强相等,由于两相的介电常数不同,两相的电位移和极板上的电荷密度不相同。
稳定条件式(16)的第1项CV>0是热稳定条件;当系统某一区域因热扰动导致温度升高时,必有热量从该区域流出,即δQ<0,由定义式δQ=CVdT及该条件可知,此时必有dT<0,从而使其温度恢复到与周围相同。第2项∂V/∂p′<0是力学稳定条件;当系统某区域因扰动导致体积增大时,则由该条件可知其压强必变小,由此导致该区域受到来自周围的压缩而恢复到压强均匀的平衡态。第3项是化学或扩散 稳 定 条 件 , 对 两 相 系 统 等 价 为 ∂μι′/∂ni>0 和∂μι′/∂nj<0;当由于涨落等因素造成某种物质在某区域富集时,该条件要求这种物质的化学势升高,而其他物质的化学势降低;这种化学势的变化将导致该种物质流向周围化学势较低的区域,周围的其他种物质流向该区域,使得该区域恢复到均匀的平衡状态。第 4项∂q/∂ζ>0是电场作用所必须满足的稳定条件,称为电稳定条件。电稳定条件要求金属极板的电荷量与极板的电压呈正比,当由于涨落或扰动造成极板某区域的电荷量增加时,由该条件可知其电势必上升,电势上升将导致电荷流向周围低电势区域,使极板的电荷恢复到均匀的平衡状态。由电磁学理论[26],∂q/∂ζ>0条件自然能得到满足,因此电场作用下的平衡是稳定平衡。
在图1所示的模型中,金属极板垂直于相界面。当系统物质发生相变时,分别位于α相和 β相中的极板面积以及极板上的电荷都会发生变化,因此电荷重新分布对系统的平衡条件及稳定条件都有影响。如果带电金属极板平行于相界面,也就是两块极板分别位于两相,则极板面积和电荷量固定,因此在相变过程中电荷分布不变。利用上面相同的方法可得出,电场参量可以改变系统的平衡条件,但对系统的稳定性没有影响。
4 静电场作用下的力学平衡条件和相变平衡条件
除热平衡条件外,式(12)给出的平衡条件不同于经典热力学中的平衡条件。式(12)力学平衡条件中的压强可称之为电场作用下的等效压强,从定义式(8)知
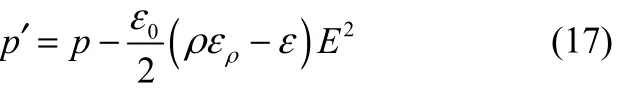
式中,右侧第1项p是施加电场作用后系统的真实压强;由电场能量微分式(6)可知,第 2项(-ε0ρερE2)/2来自于介电常数随密度的变化,第3项ε0εE2/2来自于电介质体积的变化,这两项都是电场作用产生的力学效应。
为了进一步明确等效压强式(17)的物理含义,再看一个特例。如图2所示,电场只作用在系统的下半部分。在这样的系统中两相的体积固定,因此等效压强式(17)中没有了与体积变化相关的第3项。设电场作用后,上、下部分的真实压强分别是p和pE。由式(17)得两部分的等效压强,p′α=p和p′β=pE-(ε0/2)ρερE2,再由力学平衡条件式(12) p′α=p′β得
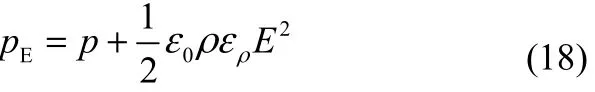
式(18)说明,平衡系统两相的真实压强不相等。电动力学已证明[25],由于分子结构的差别,静电场在电介质界面产生有力的作用,界面力与系统内部的压强一起共同构成了力学平衡条件,这一结论已被实验证实[27-28]。在图 2中这种电场界面力由α相指向β相,由此造成β相的压强大于α相的压强。这种情况类似于液滴,由于表面张力作用,液滴内部的压强大于外面的压强。
式(12)相变平衡条件中的化学势称为电场作用下的等效化学势,由定义式(8)

图2 电场中的电介质系统Fig. 2 Dielectric system in electric field
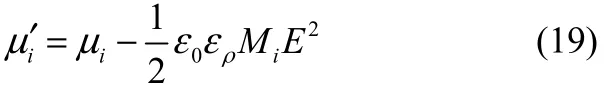
式(19)右侧第 1项就是常规的化学势,与物质的温度和浓度有关;第2项是单位摩尔物质的电场极化能量。式(19)表明,电场作用下物质的流动方向将由物质的浓度分布和电场分布共同决定。由于电场作用使物质的等效化学势减小,介电常数较大的物质将向电场较强的区域富集,平衡后系统的浓度不均匀,这一现象也已被实验证实[29-30]。这一热力学结论与动力学的结论一致,电偶极子在电场中受到沿场强梯度方向的作用力[25],在这个力作用下偶极分子向场强较强的区域运动,导致该区域浓度增加。
对于气体电介质,从相变平衡条件也可以得到等效压强,而且与统计物理学的结论一致。在图 2中,α相的化学势是μ′α=μ0(T)+RTln(p/p0),由式(19)得β相的等效化学势μ′β=μ0(T)+RTln(pE/p0)-ε0ερME2/2。再由相变平衡条件μ′α= μ′β得

通常由电场引起的压强变化比系统本身压强小很多pE/p≈1,因此可以利用泰勒级数展开得 ln(pE/p)≈(pE-p)/p。再利用理想气体方程pVm=RT及关系式M=ρVm可以将式(20)改写为与式(18)完全相同的形式。
设粒子在势场中的势能是εp,由 Boltzmann分布知粒子数密度是n=n0exp(-εp/kT),k是Boltzmann常数[1]。电介质单位体积电势能是φ=-ε0(ε-1)E2/2[25],单个粒子的电势能是εp=-ε0(ε-1)E2/2n。利用理想气体方程[2]p=nkT和Boltzmann分布得静电场作用下气体的压强

对于流体电介质,利用Clausius-Mossotti定律[31]有关系式ρερ=(ε-1)(ε+2)/3,对于气体电介质ε+2≈3,代入式(21)得到与式(20)完全相同的形式。
式(18)和式(19)是普遍化的,这两个公式适用于任何物质。只要将某一温度下物质的介电常数等物性参数代入,就可以计算出不同电场强度下压强和化学势的改变量,也就知道了静电场对系统平衡态的影响程度。例如,20℃时在场强为 1 MV·m-1的电场作用下水的压强增加了9.56 kPa,化学势减少了 0.17 J·mol-1;甲苯的压强增加了 8.91 Pa,化学势减小了0.001 J·mol-1。因为水的介电常数(80)远大于甲苯的介电常数(2.4),所以电场对水的影响远大于对甲苯的影响。
5 结 论
利用热力学定律建立了静电场作用下电介质系统的熵函数,该熵函数可以有效地描述系统的平衡态和稳定性。静电场能够改变电介质系统的平衡条件,对平衡态的稳定性也提出了新的要求。电场作用下电介质系统的平衡条件要求系统各相的温度、等效压强、等效化学势和由平行极板产生的电场强度相等;稳定条件还要求产生电场的电荷量与电势呈正比。等效压强表明,电场对电介质有力的作用,系统的力学平衡由系统的真实压强和电场界面力共同决定。等效化学势表明,电场作用下物质的扩散与温度、浓度和电场作用有关。
符 号 说 明
A ——电极板面积,m2
Cp,CV——分别为等压热容、等容热容,J·K-1
D ——电位移,C·m-2
E ——电场强度,V·m-1
k ——Boltzmann 常数,J·K-1
L ——极板间距,m
Mi——第i种组分的分子量
ni——第i种组分的物质的量,mol
p, p′ ——分别为压强、电场作用下等效压强,Pa
Q ——热量,J
q ——电荷量,C
S ——熵,J·K-1
T ——热力学温度,K
U ——内能,J
V, Vm——分别为体积、摩尔体积,m2
W ——功,J
We——电场能量,J
ε, ε0——分别为介电常数、真空介电常数,F·m-1
εp——单个粒子电势能,
J——极板间电压,V
μi——第i种组分的化学势,J·mol-1
ρ——密度,kg·m-3
σ——电荷面密度,C·m-2
φ——电势能,J
[1] 林宗涵. 热力学与统计物理学[M]. 北京: 北京大学出版社, 2007: 4.LIN Z H. Thermodynamics and Statistical Physics[M]. Beijing:Peking University Press, 2007: 4-16.
[2] SANFORD K, GREGORY N. Thermodynamics[M]. Cambridge:Cambridge University Press, 2012: 4-21.
[3] 高执棣, 韩德刚. 化学热力学[M]. 北京: 高等教育出版社, 1997:205-217.GAO Z L, HAN D G. Chemical Thermodynamics[M]. Beijing:Higher Education Press, 1997: 205-217.
[4] RAO Y V C. Chemical Engineering Thermodynamics[M]. New Delhi:Universities Press, 2015: 194-208.
[5] ATKINS P, JULIO D P. Physical Chemistry[M]. Ninth Edition.Oxford: Oxford University Press, 2010: 153.
[6] 王补宣, 杜小泽. 细竖管内流动凝结液膜的稳定性分析[J]. 化工学报, 2000, 51(1): 7-11.WANG B X, DU X Z. Stability analysis of film during flow condensation in vertical small diameter tube[J]. Journal of Chemical Industry and Engineering(China), 2000, 51(1): 7-11.
[7] 吴双应, 易甜甜, 肖兰. 基于多目标函数的亚临界有机朗肯循环的参数优化和性能分析[J]. 化工学报, 2014, 65(10): 4078-4085.WU S Y, YI T T, XIAO L. Parametric optimization and performance analysis of subcritical organic Rankine cycle based on multi-objective function[J]. CIESC Journal, 2014, 65(10): 4078-4085.
[8] 吴双应, 汪菲, 肖兰. 基于低温烟气余热发电的 Kalina 循环热经济性能分析[J]. 化工学报, 2017, 68(3): 1170-1177.WU S Y, WANG F, XIAO L. Thermo-economic performance analysis of Kalina cycle based on low temperature flue gas waste heat power generation[J]. CIESC Journal, 2017, 68(3): 1170-1177.
[9] HAQUE M F, MSHELIA E D, ARAJS S. Effect of electric fields on heat transfer in liquids[J]. Journal of Physics D: Applied Physics,1992, 25(5): 740-744.
[10] DONG Z G, CHENG D L, HUANG X. Experimental study of pool boiling heat transfer enhancement with r123 under non uniform electric field[J]. Research Journal of Applied Sciences, Engineering and Technology, 2013, 5(6): 2138-2141.
[11] 韩光泽, 杜尚永, 陈明东. 外场作用下多组分质量传递Maxwell-Stefan方程及其应用: 电场作用下球形颗粒中的扩散[J].化工学报, 2012, 63(2): 416-423.HAN G Z, DU S Y, CHEN M D. Maxwell-Stefan equation of multicomponent mass transfer under the influence of external field and its application: diffusion in spherical particle enhanced by electric field[J]. CIESC Journal, 2012, 63(2): 416-423.
[12] 韩光泽, 陈佳佳. 电场强化对流传热的热力学机理[J]. 华南理工大学学报(自然科学版), 2013, 41(12): 125-128.HAN G Z, CHEN J J. Thermodynamic mechanism of convective heat transfer enhanced by electric field[J]. Journal of South China University of Technology (Natural Science Edition), 2013, 41(12):125-128.
[13] HAN G Z, CHEN M D. Microwave peak absorption frequency ofliquid[J]. Science in China (G), 2008, 51(9): 1254-1263.
[14] 陈明东, 韩光泽, 郭平生. 微波场作用下的溶质扩散通量[J]. 工程热物理学报, 2008, 29(11): 1950-1952.CHEN M D, HAN G Z, GUO P S. Solute diffusion flux under microwave enhancement[J]. Journal of Engineering Thermophysics,2008, 29(11): 1950-1952.
[15] 韩光泽, 过增元. 导热能力损耗的机理及其数学表述[J]. 中国电机工程学报, 2007, 27(17): 98-102.HAN G Z, GUO Z Y. Physical mechanism of heat conduction ability dissipation and its analytical expression[J]. Proceedings of the CSEE,2007, 27(17): 98-102.
[16] ASAKAWA Y. Promotion and retardation of heat transfer by electric fields[J]. Nature, 1976, 261(5557): 220-221.
[17] JIA Y B, SUNGTAEK Y J. A solid-state refrigerator based on the electrocaloric effect[J]. Applied Physics Letters, 2012, 100(24):242901.
[18] SUCHANECK G, GERLACH G. Materials and device concepts for electrocaloric refrigeration[J]. Physica Scripta, 2015, 90(9):094020.
[19] WOOD S E, BATTINO R. Thermodynamics of Chemical Systems[M]. Cambridge: Cambridge University Press, 1990: 331.
[20] ADKINS C J. Equilibrium Thermodynamics[M]. Third Edition.Cambridge: Cambridge University Press, 1983: 96.
[21] 韩光泽, 华贲, 陈清林, 等. 能量的普遍化表达式与能态公设[J].华南理工大学学报(自然科学版), 2001, 29(7): 48-50.HAN G Z, HUA B, CHEN Q L, et al. The general energy expression and the energy state postulate[J]. Journal of South China University of Technology (Natural Science Edition), 2001, 29(7): 48-50.
[22] HAN G Z, HUA B, CHEN Q L. Generalized expression of exergy in the thermodynamics[J]. Science in China(A), 2002, 45(1): 70-75.
[23] HAN G Z, HUA B. Energy postulate and generalized expressions of energy and exergy[C]//Proceedings of ECOS 2004. Guanajuato,Mexico, 2004, 23(1): 753-760.
[24] HAN G Z, WANG H J. Generalized expression of chemical potential with influence of external fields and its applications: effect of charged particles on droplet condensation[J]. Fluid Phase Equilibria, 2013,338(11): 269-273.
[25] LANDAU L D, LIFSHITZ E M. Electrodynamics of Continuous Media[M]. 2nd Edition. Oxford: Pergamon Press, 1984: 52-92.
[26] STRATTON J A. Electromagnetic Theory[M]. New Jersey: John Wiley & Sons, 2007: 85-92.
[27] HAKIMT S S, HIGHAM J B. An experimental determination of the excess pressure produced in a liquid dielectric by an electric field[J].Proceedings of the Physical Society, 1962, 80(1): 190-198.
[28] ISRAELSSON U E, JACKSON H W, PETRAC D. Liquid/vapour phase separation in 4He using electric fields[J]. Cryogenics, 1988,28(2): 120-125.
[29] LEE K Y C, KLINGLER J F, HARDEN M M. Electric field-induced concentration gradients in lipid monolayers[J]. Science, 1994,263(5174): 655-658.
[30] GAO G T, OH K J, ZENG X C. Effect of uniform electric field on homogeneous vapor-liquid nucleation and phase equilibria(Ⅱ ):Extended simple point charge model water[J]. The Journal of Chemical Physics, 1999, 110(5): 2533-2538.
[31] BOTTCHER C J F. Theory of Electric Polarization[M]. Amsterdam:Elsevier, 1973: 75-137.
Equilibrium state and its stability of dielectric system acted by electrostatic fields
HAN Guangze, MA Lehan
(Department of Physics, South China University of Technology, Guangzhou 510641, Guangdong, China)
Thermodynamic equilibrium state has the lowest possible energy, any non-equilibrium state is approaching equilibrium state unless existing external interactions and unified state parameters can be assigned only to the equilibrium state. Electromagnetic field can effectively enhance the heat and mass transfer processes,and it also has obvious effects on the equilibrium and stability of dielectric system. Based on the first and the second law of thermodynamics, the electric field energy is introduced into the thermodynamic differential equation, from which a new entropy function of dielectric system with the influence of electric field is deduced.Then, the equilibrium conditions and the stable conditions of dielectric systems under the action of electrostatic field are derived from the entropy criterion. The new equilibrium conditions require that the temperature, effective pressure, effective chemical potential, and electric field are uniform through the whole system. The new stable conditions require that the electric charge on the metal plates is proportional to the electric potential. This effective pressure includes mechanical effect from polarization, and the mechanical equilibrium is determined by real pressure and the electric polarization force. The effective chemical potential includes the effect of polarization potential energy, and the phase equilibrium is determined by concentration and polarization potential energy. The thermodynamic conclusions are consistent with that of electrodynamics and statistical physics, which have beenconfirmed by experiments.
thermodynamics; entropy; phase equilibria; vapor liquid equilibria; stability
date:2017-01-12.
Prof. HAN Guangze, phgzhan@scut.edu.cn
supported by the National Natural Science Foundation of China (51576068).
TB 131; TK 121
A
0438—1157(2017)07—2660—07
10.11949/j.issn.0438-1157.20170055
2017-01-12收到初稿,2017-02-27收到修改稿。
联系人及第一作者:韩光泽(1964—),男,博士,教授。
国家自然科学基金项目 (51576068)。

