软弱地层中桥梁桩基负摩阻力分析方法研究
唐 雷
(湖南尚上建设开发有限公司,湖南 长沙 410003)
软弱地层中桥梁桩基负摩阻力分析方法研究
唐 雷
(湖南尚上建设开发有限公司,湖南 长沙 410003)
鉴于软土地基中桥梁桩基的负摩阻力问题,基于土体应力应变双曲线模型,考虑桩周土固结过程中的非线性特征,以及由此带来土体变形指标的变化,引入桩土相互作用同心圆模型,结合相应的边界与连续性条件,建立了考虑桩周土非线性固结的基桩负摩阻力分析方法,并采用某工程算例对本文方法进行了验证,结果表明该方法是合理可行的,可对桥梁桩基设计计算以及施工方案选取提供一定的理论支持。
桥梁工程;桩基;荷载传递;负摩阻力;固结;双曲线模型
0 引言
随着我国高速交通事业的不断发展,高速公路与高速铁路需跨越大量的深厚软土区域,软土由于固结沉降引起的负摩阻力问题是软土桩基在设计计算与施工方案制定中面临的主要问题,也是目前桥梁桩基领域研究的热点问题[1,2]。
就目前情况来说,在该领域,弹性理论法应用较为广泛,如Poulos[3]运用Mindlin解建立的端承桩负摩阻力分析方法,赵明华等[4]基于荷载传递与Bousinnesq解建立的考虑桩土滑移的基桩负摩阻力分析方法,以及Wong[5]等基于桩土界面双曲线模型建立的基桩负摩阻力分析方法等。然而弹性理论法的优势是计算较为简便,但无法考虑桩土相互作用的失效性。于是,部分学者从桩周土的角度出发来分析桩土相互作用中的负摩阻力问题。Poulos[6]等基于Terzaghi固结理论,获得了单桩负摩阻力随时间的发展规律,但未考虑桩土相互作用;屠毓敏[7]同样采用Terzaghi固结理论研究桩周土的竖向变形,并结合桩土荷载传递模型,获得了基桩负摩阻力分析方法,但该方法未考虑桩周土的非线性。
大量研究表明,软土地基在固结过程中呈非线性变形特性,其物理力学指标也随之不断改变,为此,本文引入魏汝龙[8]提出的土体应力应变双曲线模型,考虑桩周土固结变形,以及随之带来的土体变形指标的变化,结合桩土荷载传递的同心圆模型,建立了桩土相互作用同心圆模型,建立了软土地层中基桩负摩阻力分析模型,以期为该领域的桥梁桩基设计计算与施工方案制定与优化提供一定的理论支持。
1 桩土荷载传递分析
Alonso[9]采用同心圆筒模型模拟桩与桩周土的相互作用以及剪力在桩间土中的传递,如图1所示,根据几何关系可得:
(1)
式中:Gs为桩周土剪切模量,这里取割线模量;ws与wp分别为桩间土与桩身位移:rp为桩身半径:rm为桩对桩周土影响半径,一般取rm=2.5ρg(1-vs)Lp,其中ρg为不均匀系数,取决于桩身中部土与桩端土,Lp为桩长;τps为桩土界面摩阻力。
如图2所示,根据桩身微单元竖向受力平衡,可得:

(2)
式中,p为桩身轴力。

图1 荷载传递同心圆筒模型

图2 桩身微单元竖向受力分析
结合桩身物理方程与式(1),将积分项积分,可将式(2)转化为:

(3)
至此,获得了压缩层中桩土荷载传递控制方程,其中,土体剪切模量Gs不仅与埋深有关,随着土层的不断固结,Gs也会不断发生变化。
2 桩侧土体固结沉降分析
2.1 土体应力应变模型
如图3所示,魏汝龙[8]基于大量试验数据,发现采用双曲线模拟土体应力应变关系,较为合适且参数取值也较为简单。

图3 双曲线应力应变模型
基于上述成果,在图3坐标系中,割线压缩模量Ec、孔隙比e与有效应力的关系分别为:
(4)
式中:σ′为竖向有效应力;A、B为试验确定的相关参数;e0为初始孔隙比。
某一时刻t,压缩层有效应力沿深度分布为:
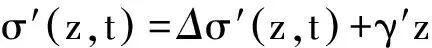
(5)
式中: Δσ′为t时刻压缩层增加的有效应力。
结合式(4)与式(5),可得剪切模量桩周土Gs:

(6)
式中:vs为桩周土泊松比。
2.2 桩周土变形分析
(7)
式中:cv为固结系数。
对于上述方程,文献[10]给出了单面排水条件下的解:
(8)
其中:

(9)

则t时刻,桩侧土沉降量ws为:
(10)
将式(8)代入式(10)并积分,可得:
(11)
根据式(11),t时刻桩周土体的平均固结度U为:
(12)
当固结度大于30%时,可近似地取级数第1项,即m=1时,则:
(13)
3 基桩变形计算
3.1 非压缩层桩土荷载传递分析
参照以往研究成果,本文假定桩周非压缩层不发生变形,根据Aloson方程[9],可有:
(14)
结合式(2)与式(14),非压缩层桩身竖向位移控制方程为:

(15)
解方程(15),可得:
wp=C1eβ z+C2e-β z
(16)
式中: C1、C2为待定系数;
(17)
3.2 压缩层桩身变形计算


图4 压缩层桩土单元划分
将式(13)代入式(3)中,可得i单元内,桩身变形控制方程为:
(18)
解上述方程,可得:

(19)
式中: Ci,1与Ci,2为待定系数;
(20)
3.3 桩身沉降计算
根据上述分析可知,求解压缩层与非压缩层中桩身需结合桩顶荷载条件、桩端变形条件以及桩身各段的连续性条件。
在桩顶荷载p作用下,有:
(21)
桩端边界条件,分为两种情况,一是桩端处于压缩层,此时有:
(22)
式中:wpb与wsb分别为桩端平面桩与桩周土变形;Gb与vsb分别为桩端土剪切模量与泊松比;αb为桩端承载力水平系数;pb为桩端截面应力。
二是桩端处于非压缩层,此时桩周土不发生变形,可得:
(23)
压缩层各单元以及压缩层与非压缩层之间的连续性条件分别为:
(24)
联立式(21)~式(24),形成代数方程组,解出待定系数,继而获得桩顶沉降。
4 算例验证
某高速公路[11]桥台进行计算分析采用钢筋混凝土灌注桩,桩径dp为1.5m,设计桩长Lp为28m,桩身模量Ep为25GPa,土层依次为淤泥层、砂土层、黏土层以及岩层,各土层物理力学参数如表1所示。原地基上填4.5m厚填土,折合荷载72kPa,当基桩沉降到达188mm时,桩身轴力计算与实测结果对比如图5所示,需要说明的是本文取软土层为压缩层,即H为13.0 m,软土压缩试验参数取A为2 000 kPa,B为4.0。

表1 土层物理力学参数

图5 桩身轴力计算结果与实测值比较
本文通过地表沉降反算地基土固结度,从而得出桩身轴力,从图5看出,本文计算方法所得出的桩身轴力变化曲线与实测结果较为接近,证明了本文方法的合理性,说明本文方法可为工程实践提供指导。从对比中可以看出,桩身轴力计算值略小于实测值,这是由于本文方法未考虑砂层与黏土层的变形,从而得出的桩土相对位移较小,桩土摩阻力较小导致的。
5 结论
本文基于土体σ—ε双曲线模型,考虑桩周土非线性固结对桩周土变形影响,以及由此带来土体应力状态变化对其力学参数的影响,引入桩土相互作用同心圆模型,结合相应的边界与连续性条件,建立了考虑桩周土非线性固结的基桩负摩阻力分析方法,并采用某工程算例对本文方法进行了验证,结果表明本文方法是合理可行的,可对桥梁桩基设计计算与施工方案优化提供一定的理论支持。
[1] 王瑞. 桥梁群桩基础沉降的数值分析[J]. 公路工程, 2014, 39(2): 227-231.
[2] 杨岳华, 刘永键, 邓淑飞, 等. 沉降控制的单桩竖向承载力及其数值分析方法[J]. 公路工程, 2008, 33(4): 133-136.
[3] Poulos H G, Mattes N S. The analysis of down-drag in end-bearing piles[C]. Proceedings of the 7th International Conference on Soil Mechanics and Foundations Engineering, Mexio, 1969.
[4] 赵明华, 贺炜, 曹文贵. 基桩负摩阻力计算方法初探[J]. 岩土力学, 2004(9): 1442-1446.
[5] Wong K S, Teh C I. Negative skin friction on piles in layered soil deposits[J]. Journal of Geotechnical Engineering, 1995, 121(6): 457-465.
[6] Poulos H G,Davis E H.The development of negative frication with time in end-bearing piles[J]. Australian Geomechanics, 1972, 62(1): 11-20.
[7] 屠毓敏, 俞洪良. 负摩擦桩非线性分析[J]. 中国公路学报, 2001(1): 33-36.
[8] 魏汝龙. 整理压缩试验资料的一种新方法[J]. 水利水运科学研究, 1980(3): 90-93.
[9] Alonso E E, Josa A, Ledesma A. Negative skin friction on piles: a simplified analysis and prediction procedure[J]. Geotechnique, 1984, 34(3): 341-357.
[10] 孔纲强, 陈力恺, 刘汉龙. 考虑土体非线性固结沉降的复合地基桩侧负摩阻力研究[J]. 中国公路学报, 2013(3): 37-43.
[11] 陈福全, 龚晓南, 马时冬. 桩的负摩阻力现场试验及三维有限元分析[J]. 建筑结构学报, 2000, 21(3): 77-80.
1008-844X(2017)02-0240-04
U 445.55
A

