基于物质点法考虑剪胀特性的土质边坡稳定性分析

姚 云

(怀化市农村公路建设办公室，湖南 怀化 418000)

基于物质点法考虑剪胀特性的土质边坡稳定性分析

姚 云

(怀化市农村公路建设办公室，湖南 怀化 418000)

自然界中的土体其体积变形往往具有剪胀特性，为了探究土体的剪胀特性对土质边坡稳定性的影响，采用物质点法模拟了具有不同剪胀角大小的土质边坡的滑动破坏全过程。计算结果表明，随着土体剪胀角的逐渐增大，土质边坡的滑动破坏区域逐渐减小，并且其最终的滑动距离也相应地减小，表明增大土体的剪胀角能够有效地提高土质边坡的稳定性，在实际工程应用中具有一定的指导意义。最后初步探究了采用最终滑动距离作为土质边坡稳定性指标的补充的可行性。

土质边坡；剪胀特性；物质点法；大变形破坏

0 引言

在地震或强降雨等自然因素的作用下边坡可能发生失稳破坏，产生大面积滑塌，造成严重的经济损失。针对边坡的稳定性分析和破坏机理探究引起了广大学者极大的关注，人们对此展开了大量的研究，并且取得了很多有益的成果。

近些年，随着计算机运算水平的提升，数值模拟方法，尤其是有限单元法在岩土工程领域具有广泛的应用。然而，由于边坡在滑动破坏的过程中会产生很大的变形，采用传统的有限单元法处理该问题时，在计算的过程中会出现网格畸变的问题，导致计算结果不收敛。物质点法作为一种新型的无网格粒子法，能够有效地避免计算过程中可能出现的网格畸变的问题，能够模拟连续介质任意大变形问题。物质点法由Sulsky等[1]首先提出，采用欧拉和拉格朗日双重描述，即采用质点离散材料区域，用背景网格计算空间导数和求解动量方程。根据现有的资料，物质点法被大量应用于边坡稳定性分析。Andersen等[2]采用物质点法分析了边坡失效过程。廉燕平等[3]应用自适应物质点有限元法分析了边坡的失效问题，计算结果表明物质点能够较好地模拟边坡失稳破坏的全过程。王双等[4]提出物质点强度折减法计算了不同安全系数下边坡内部等效塑性变形的分布特点。

然而，上述研究在采用物质点法探究边坡滑动破坏机理时并没有考虑土体剪胀特性对其安全系数的影响。Sloan等[5]指出在计算边坡安全系数时有必要考虑土体的剪胀特性，其对于边坡内部滑动面的形成过程具有显著的影响。张培文等[6]采用强度折减法计算边坡安全系数时考虑了土体的剪胀特性，计算结果表明，随着土体剪胀角的逐渐增大边坡的安全系数逐渐增大。

本文考虑土体的剪胀特性，采用物质点法分别模拟了不同剪胀角下的边坡滑动破坏过程。计算结果土体的剪胀特性对于边坡内部的等效应变的分布具有显著的影响，并且从能量的角度对该现象进行了一定程度的解释。

1 物质点法

物质点法最主要的特点在于其采用欧拉和拉格朗日双重描述。物质点法采用质点积分，将积分转化为被积函数在各质点处的值与该质点所代表的体积之积的和。物质点法的背景网格旨在为每个计算步内和物体固连，在每个计算步结束后丢弃已经变形的背景网格。由于质点已经携带了物质体的所有物质信息，在下一个时刻，可以通过将指点的信息映射到新的背景网格上来求得网格的信息，因此在物质点法中不需要记录每个时刻网格节点的任何信息，如图1所示。

在显示物质点法求解过程，应力更新主要有两种方法，一是在每个计算时间步开始时进行，称为USF方法，二是在每个计算步结束后进行，称为USL。Naim等指出USF格式具有较好的能量守恒性。 物质点法的求解过程主要包含以下几方面：

1)将每个质点的质量和动量映射到网格上，计算背景网格节点的质量和动量；

2)对节点动量施加本质边界条件；

3)由网格节点的动量计算节点速度，由此计算每个质点的应变增量和旋量增量，并对各支点的密度和应力进行更新；

4)计算背景网格节点力；

5)在背景网格节点上对动量方程进行积分；

6)将背景网格节点的速度变化量和位置变化量映射回相应的节点；

7)生成新的规则的背景网格，开始下一步的计算。

在整个计算过程中，计算信息在物质点和背网格间相互映射，能够有效地避免网格畸变和欧拉对流项处理。

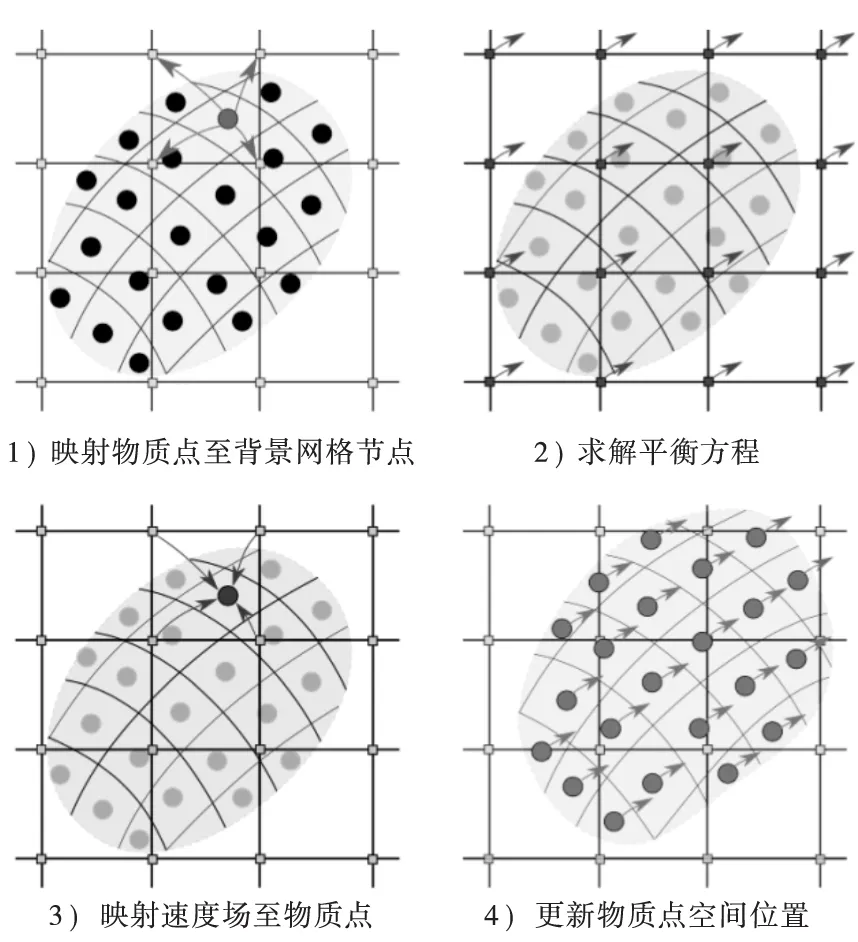
图1 物质点法计算过程示意图

2 边坡稳定性分析

2.1 考虑剪胀特性的土体力学模型

边坡的稳定性分析一直是岩土领域的一个热点的研究课题，通常采用安全系数来评价其稳定性。在具体求解边坡安全系数的过程中，很多学者忽略了土体剪胀特性对土体力学特性的影响。为了考虑土体的剪胀特性，本文采用非关联的莫尔-库仑弹塑性模型描述土体的力学特性。

莫尔-库伦弹塑性模型塑性势函数和屈服方程有如下形式:

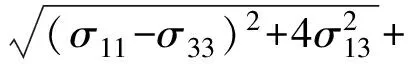
(1)

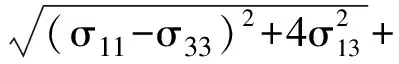
(2)

其中，φ为内摩擦角;c为黏聚力;ψ为膨胀角。

由于本文中采用张雄等[7]研发的MPM3 D程序，其内部只包含了Drucker-Prager弹塑性模型，在实际计算的过程需要将莫尔-库伦弹塑性模型的参数进行转化。

Drucker-Prager弹塑性模型的屈服函数为：

(3)

其中，J2为偏应力张量的第2不变量；σm为球应力；α为摩擦系数；k为纯剪切状态时的屈服应力。

材料参数α、k和c、φ之间的关系如下：

(4)

(5)

在张雄等所给出的Drucker-Prager弹塑性模型中，剪切式函数ψs具有如下表达式：

ψs=βσm

(6)

其中，β为考虑剪胀特性的力学参数，其与土体的剪胀角ψ之间具有如下关系。

(7)

2.2 计算模型

在实际工程应用中，由于人工开挖等因素的影响，道路两旁的边坡中的土体往往具有超固结性，在自身重力或外部荷载的作用下其体积会发生剪胀，进而对边坡的稳定性产生影响。为了探究不同剪胀角所对应的土体内部等效塑性变形的分布，本文假定土体的剪胀角为0°、5°、10°、15°、30°和45°这6种情况针对均质土质边坡进行数值模拟，计算模型如图2所示。

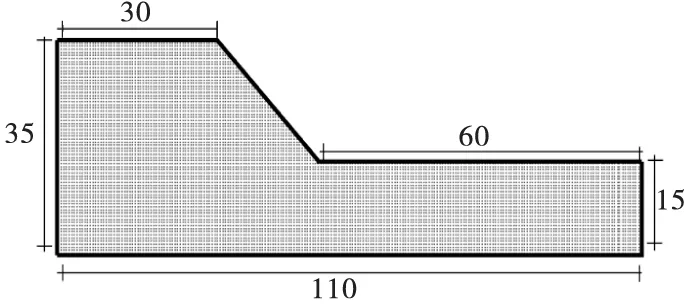
图2 土质边坡计算模型(单位：m)

计算模型中的物质点数目为11 968个，计算模型的参数如表1所示。

表1 模型计算参数

每个计算步的时间为0.1 s，总的计算时间为15 s。

2.3 计算结果及分析

不考虑土体剪胀角时，土质边坡在自身重力的作用下发生滑动破坏，如图3所示，可以看出，土质边坡坡脚处首先发生屈服，产生较大的等效塑性变形，并且沿着滑动破坏面向上扩展，当滑动破坏面完全贯通后，土质边坡发生大变形破坏。由于物质点法属于无网格法，在计算模型产生较大的体积变形时，不需要考虑网格畸变所带来的计算结果发生不收敛的问题，因此能够采用物质点法准确模拟土质边坡的滑动破坏全过程，为后面探究土体剪胀特性对边坡稳定性的影响打下了良好的基础。

图3 不考虑剪胀特性时土质边坡滑动破坏全过程(等效塑性变形)

不同剪胀角下土体边坡最终的滑动形态如图4所示，可以看出，随着剪胀角的逐渐增大，该边坡的最终滑动距离逐渐减小，另外，该边坡滑动区的范围也逐渐的减小。该计算结果表明随着土体剪胀角的逐渐增大，土质边坡的稳定性会逐渐增大，该结论与增大土体剪胀角会导致土体的安全系数增大的结论保持一致。

本文计算的土质边坡最终滑动距离随土体剪胀角的变化曲线如图5所示，可以看出，随着剪胀角的增大，土质边坡的最终滑动距离逐渐减小，并且具有较好的线性规律。

图4 土体剪胀特性对土质边坡最终的破坏形态的影响(等效塑性变形)

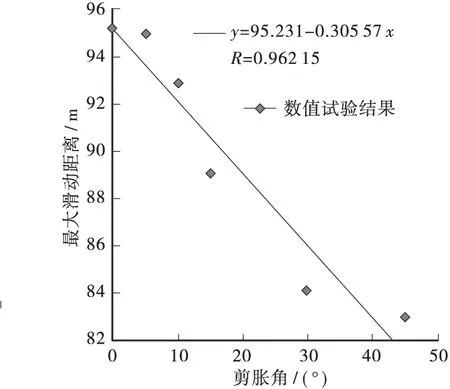
图5 土质边坡最终的滑动距离随土体剪胀角的变化规律

值得注意的是，在实际工程应用通常采用安全系数作为边坡稳定性大小的评判指标。然而安全系数主要考虑边坡不发生滑动破坏的情况。事实上，对于一些安全性要求并不是很高的边坡，在治理的过程中只需要保证边坡最终的滑动距离远离附近的建筑物，因此可以采用物质点法等数值计算手段计算得到边坡的最终滑动距离，根据其与附近建筑物的距离进行相应的治理，进而节约治理成本。

不同剪胀角下土质边坡在滑动破坏的过程中总动能和总内能随着计算时间的变化规律如图6、图7所示。根据图6可以看出，随着计算时间的增大土质边坡内部的总动能先逐渐增大，达到峰值后逐渐减小。并且随着土体剪胀角的增大土质边坡总动能峰值逐渐增大。根据图7可以看出随着随着计算时间的增大土质边坡的总内能逐渐增大，最终趋于稳定，并且随着土体剪胀角的增大，土质边坡的总内能逐渐增大。

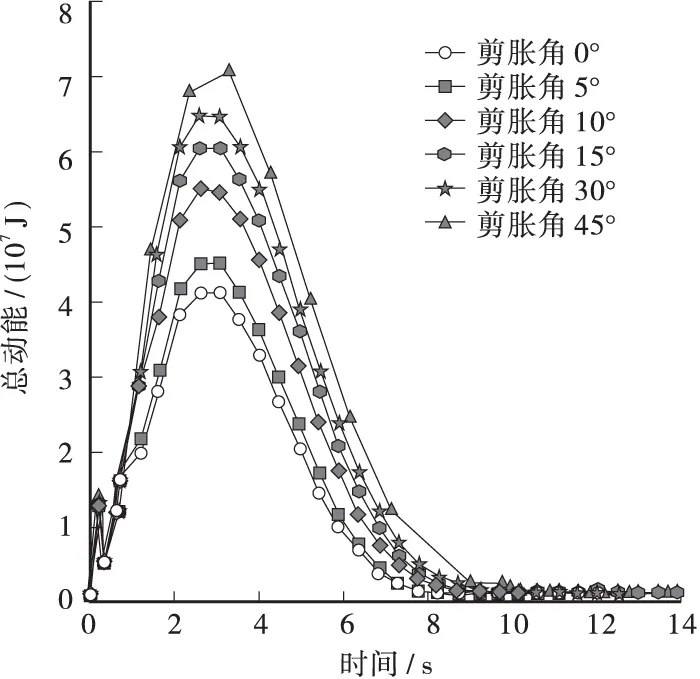
图6 不同剪胀角下土质边坡滑动破坏过程中总动能随时间的变化规律

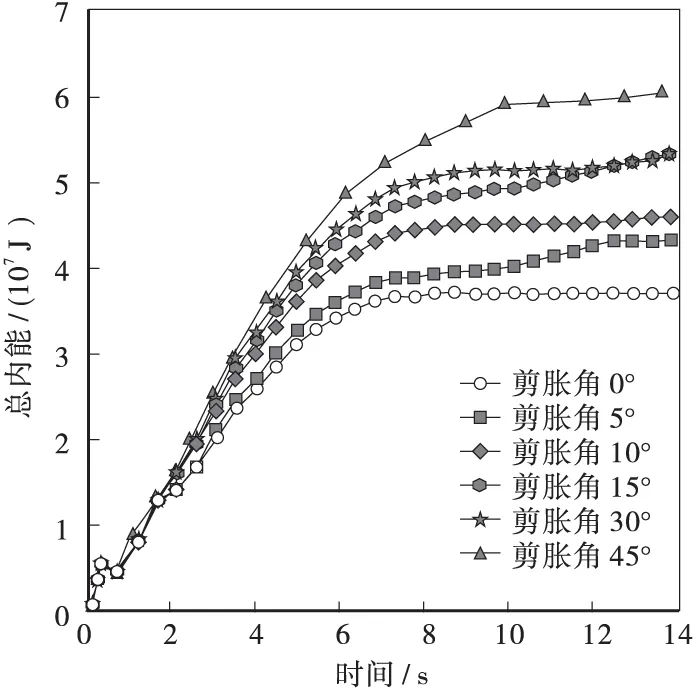
图7 不同剪胀角下土质边坡滑动破坏过程中总内能随时间变化规律

3 结论

本文采用物质点法对土质边坡开展了一系列的数值试验，重点探究了土体剪胀特性对边坡稳定性的影响，主要结论有：

1)物质点法能够较好地模拟边坡的滑动破坏全过程，能够用来探究不同影响因素对边坡稳定性的影响。

2)土体剪胀角对边坡的滑动机理具有显著的影响，表现为随着剪胀角的增大，土质边坡的最终滑动距离逐渐减小，土质边坡的稳定性逐渐增大。

3)边坡最终的滑动距离可以作为边坡稳定性分析的新的参考指标，考虑边坡的失稳破坏对临近建筑物的影响，从而缩减边坡治理成本。

[1] Sulsky D, Schreyer H L. Axisymmetric form of the material point method with applications to upsetting and Taylor impact problems[J]. Computer Methods in Applied Mechanics & Engineering, 1996, 139(1):409-429.

[2] Andersen S, Andersen L. Modelling of landslides withthe material-point method[J]. Computational Geosciences, 2010, 14(1):137-147.

[3] 廉艳平, 张帆, 刘岩,等. 物质点法的理论和应用[J]. 力学进展, 2013, 43(2):237-264.

[4] 王双, 李小春, 石露,等. 物质点强度折减法及其在边坡中的应用[J]. 岩土力学, 2016, 37(9):2672-2678.

[5] Tschuchnigg F, Schweiger H F, Sloan S W. Slope stability analysis by means of finite element limit analysis and finite element strength reduction techniques. Part I: Numerical studies considering non-associated plasticity[J]. Computers & Geotechnics, 2015, 70:169-177.

[6] 张培文, 陈祖煜. 剪胀角对求解边坡稳定的安全系数的影响[J]. 岩土力学, 2004, 25(11):1757-1760.

[7] 张雄, 宋康祖, 陆明万. 无网格法研究进展及其应用[J]. 计算力学学报, 2003, 20(6):730-742.

1008-844X(2017)02-0082-04

U 416.1+4

A