耦合Burgers方程的Darboux变换及精确解

吴丽华， 赵倩

(华侨大学 数学科学学院， 福建 泉州 362021)

耦合Burgers方程的Darboux变换及精确解

吴丽华， 赵倩

(华侨大学 数学科学学院， 福建 泉州 362021)

通过引入与耦合Burgers方程相联系的3×3矩阵谱问题的规范变换，构造出耦合Burgers方程的一个Darboux变换，并由此得到了它的一些精确解. 关键词： 耦合Burgers方程； 规范变换； Darboux变换； 精确解

孤子理论不仅在水波，而且在等离子体、固体物理、光学、医学等领域都有广泛的应用.随着研究的深入，涌现了很多经典求解孤子方程的方法，如反散射变换[1-2]、Hirota双线性方法[3]、Painlevé分析[4-5]、代数几何法[6-7]、Darboux变换[8-9]等.其中，Darboux变换是最有效、直接的求解方法之一.通过考虑一个3×3矩阵谱问题，Geng等[10]发现了一个新的耦合Burgers方程，即

(1)

并建立了它的bi-Hamiltonian结构.当u=v=r=0时，方程(1)可约化为经典的Burgers方程.本文主要构造耦合Burgers方程(1)的Darboux变换，并讨论它的精确解.

1 耦合Burgers方程的Darboux变换

考虑与耦合Burgers方程相联系的3×3矩阵谱问题，即

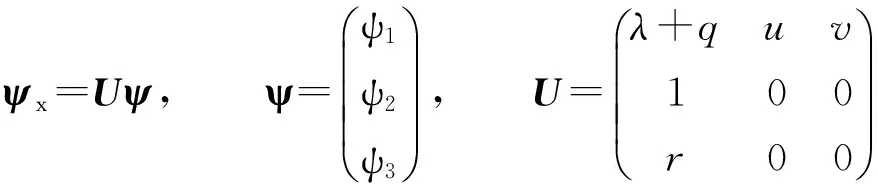
(2)

及辅谱问题

(3)

式(2)，(3)中:q,r,u,v是4个位势；λ是常数谱参数.直接计算可知，零曲率方程Ut-Vx+[U,V]=0可导出耦合Burgers方程(1).

引入谱问题(2)，(3)的一个规范变换，即

(4)

式(4)中的a和bi，j(i,j=1,2,3)将在下文定出.

显然，矩阵T的行列式det T是关于λ的三次多项式.令λj(j=1,2,3)为3个任意给定的常数且为行列式detT的根.于是，

(5)

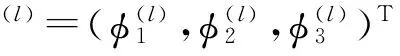
(6)

方程(6)可改写为

(7)

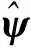
(8)

其中,有

(9)

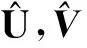
(10)

变换(10)称为耦合Burgers方程(1)的一个Darboux变换.

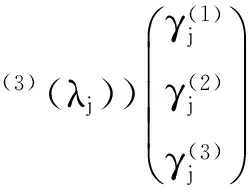
(11)

对式(11)关于x求导，并联立式(11)，可得

(12)

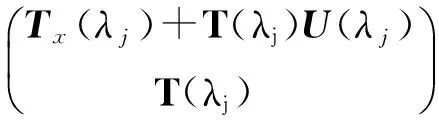
(13)

令(Tx+TU)T*=(fs，l(λ))3×3，显然，fs，l(λj)=0(s,l,j=1,2,3).经计算可知，f1，1(λ)是λ的四阶多项式；f1，2(λ),f1，3(λ),f2,1(λ),f3，1(λ)是λ的三阶多项式；f2，2(λ),f2，3(λ),f3，2(λ),f3，3(λ)是λ的二阶多项式.因此，f2，2(λ)=f2，3(λ)=f3，2(λ)=f3，3(λ)，且

(14)

其中，有

(15)

又T-1=T*/detT,于是式(14)可写为

(16)

比较(16)中λ2,λ1,λ0的系数，可得

(17)

和一些恒等式，即有

(18)

(19)

同理，有

(20)

令(Tt+TV)T*=(gs，l(λ))3×3，显然gs，l(λj)=0(s,l,j=1,2,3).通过计算可知，g1，1(λ)是λ的五阶多项式；g1，2(λ),g1，3(λ),g2，1(λ),g3，1(λ)是λ的四阶多项式；g2，2(λ),g2，3(λ),g3，2(λ),g3，3(λ)是λ的三阶多项式.于是，有

(21)

式(21)中：

(22)

比较式(21)中λ的同次幂系数，并应用恒等式(18)，有

(23)

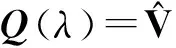
由此可见，规范变换(4)将耦合Burgers方程(1)的谱问题(2),(3)变成了形式完全一致的谱问题(8)，称规范变换(4)为谱问题(2),(3)的一个Darboux变换.于是，可得如下结论.

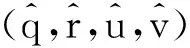
2 精确解

应用Darboux变换(10)讨论耦合Burgers方程(1)的精确解.依据Cramer法则，可从式(7)中解得a,b1，2,b1，3和b3，1分别为

(24)

式(24)中：

(25)

1) 选取耦合Burgers方程(1)的初始解q=r=u=v=0，则谱问题(2)，(3)简化为

(26)

它的一个基解矩阵是

(27)

由式(7)的定义和式(27)，可得

(28)

应用Darboux变换(10)，可得耦合Burgers方程(1)的一个精确解，即

(29)

式(29)中:Δ,Δi(i=1,2,3,4)由式(25)定义.

2) 选定耦合Burgers方程(1)的初始解q=u=v=0,r=1，则谱问题(2),(3)变为

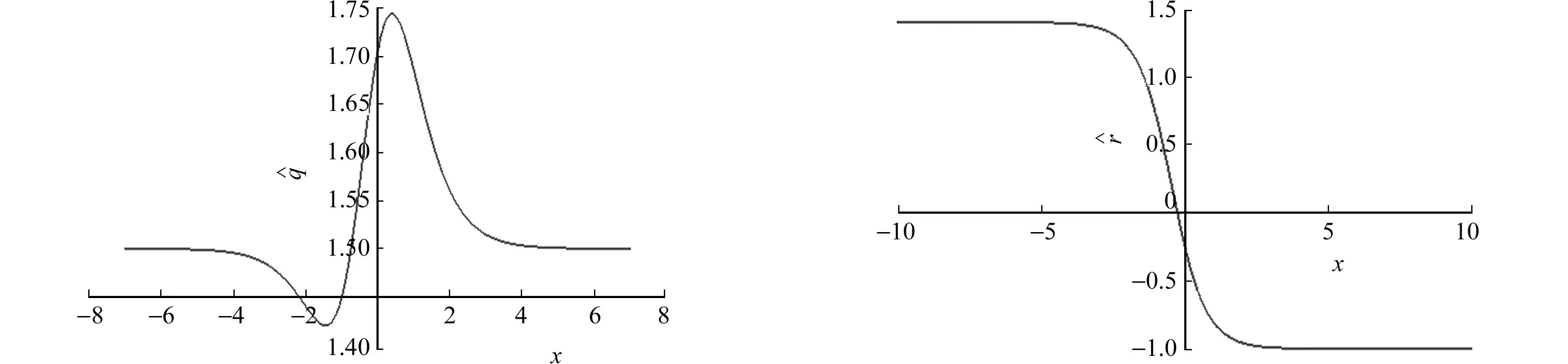
(a) t=0时的时的

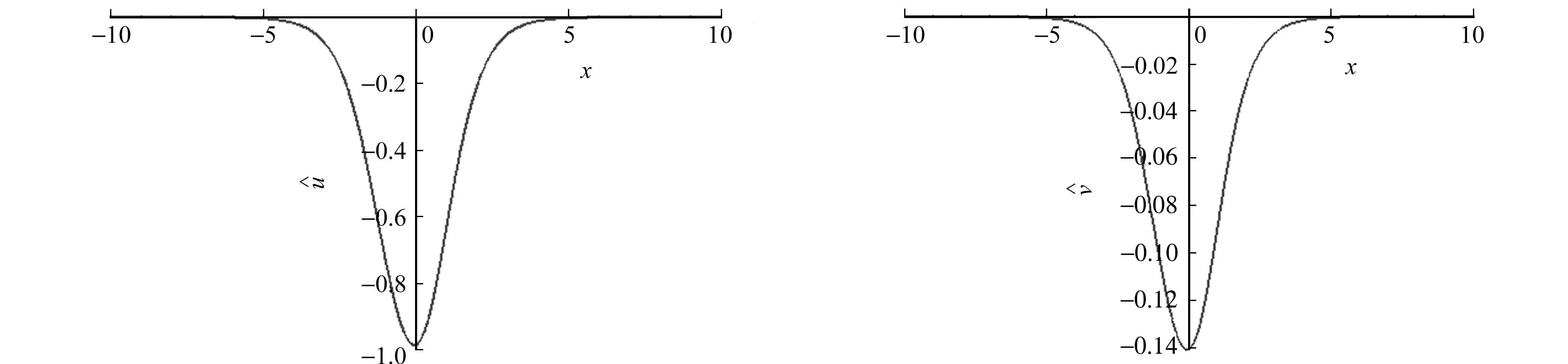
(c) t=0时的时的图1 式(29)中的孤子解Fig.1 Soliton solution in formula (29)

(30)

它的一个基解矩阵为

(31)

由式(7)的定义和式(31)，可得

(32)

应用Darboux变换(10)，得到耦合Burgers方程(1)的一个精确解,即

(33)

式(33)中:Δ,Δi(i=1,2,3,4)由式(25)定义.

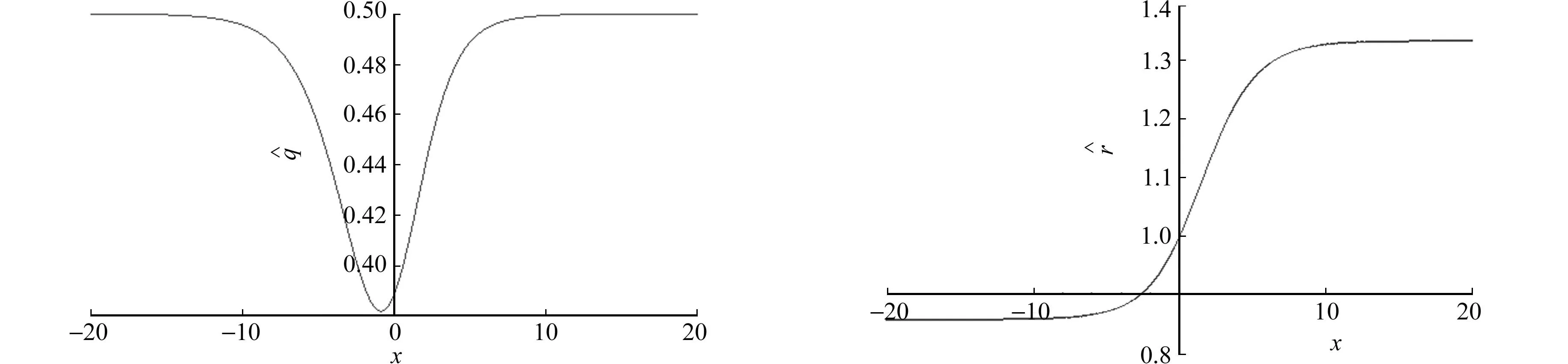
(a) t=0时的时的

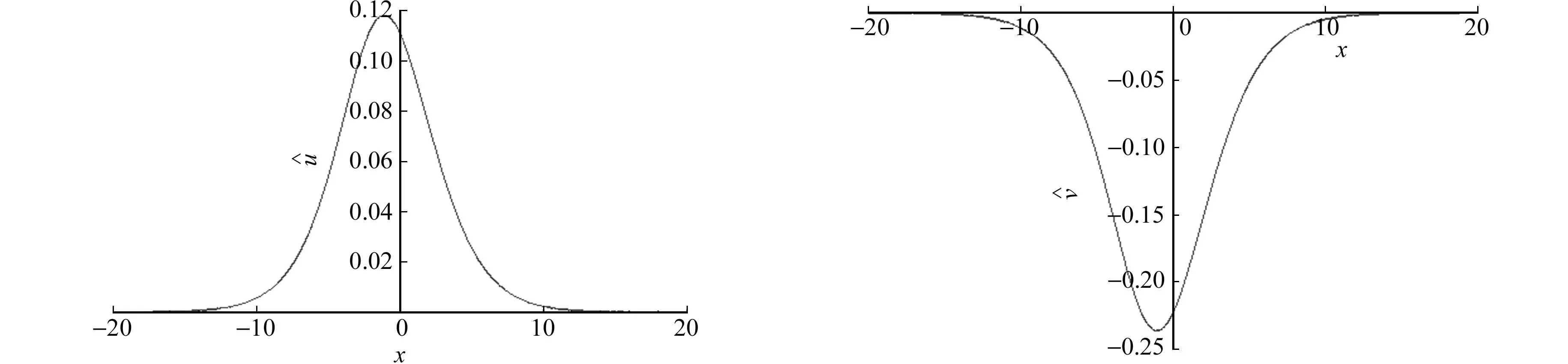
(c) t=0时的时的图2 式(33)中的孤子解Fig.2 Soliton solution in formula (33)

3) 选取耦合Burgers方程(1)的初始解q=r=u=0,r=1，可得耦合Burgers方程(1)的一个精确解,即

(34)

式(34)中:Δ,Δi(i=1,2,3,4)由式(25)定义,且有

(35)

4) 选取耦合Burgers方程(1)的初始解q=r=v=0,u=1，可得耦合Burgers方程(1)的一个精确解，即

(36)

式(36)中:Δ,Δi(i=1,2,3,4)由式(25)定义,且

(37)

3 结束语

通过引入谱问题的规范变换，构造出耦合Burgers方程的一个Darboux变换.选取耦合Burgers方程的4个平凡的初始解，应用Darboux变换，得到了它的4个精确解.在此基础上，适当选取参数，给出耦合Burgers方程的两个孤子解,并画出了t=0时相应位势的平面图.

[1]ABLOWITZMJ,KAUPDJ,NEWELLAC.Theinversescatteringtransform-Fourieranalysisfornonlinearproblems[J].StudApplMath,1974,53(4):249-315.

[2]ABLOWITZMJ,SEGURH.Solitonsandtheinversescatteringtransform[M].SIAM:Philadelphia,1981.

[3]HIROTAR.Thedirectmethodinsolitontheory[M].Cambridge：CambridgeUniversityPress,2004.

[4]ABLOWITZMJ,RAMANIA,SEGURH.Aconnectionbetweennonlinearevolutionequationsandordinarydifferentialequationsofp-typeⅠ[J].MathPhys,1980,21(4):715-721.

[5]ABLOWITZMJ,RAMANIA,SEGURH.Aconnectionbetweennonlinearevolutionequationsandordinarydifferentialequationsofp-typeⅡ[J].MathPhys,1980,21(5):1006-1015.

[6]NOVIKOVSP.TheperiodicproblemfortheKorteweg-devriesequation[J].FunctAnalAppl,1974,8(3):236-246.

[7]ITSAR,MATVEEVVB.Schrödingeroperatorswithfinite-gapspectrumandN-solitonsolutionsoftheKorteweg-deVriesequation[J].TheorMathPhys,1975,23(1):51-68.

[8]MATVEEVVB,SALLEMA.Darbouxtransformationandsolitons[J].JournalofNeurochemistry,1991,42(6):1667-1676.

[9] 谷超豪,胡和生,周子翔.孤立子理论中的达布变换及其几何应用[M].2版.上海：上海科学技术出版社,2005.

[10] GENG Xianguo,WANG Hui.A hierarchy of new nonlinear evolution equations and their bi-Hamiltonian structures[J].Chin Phys Lett,2014,31(7):5-8.

(责任编辑： 黄晓楠 英文审校： 黄心中)

Darboux Transformation and Exact Solutions to Coupled Burgers Equation

WU Lihua， ZHAO Qian

(School of Mathematical Sciences, Huaqiao University, Quanzhou 362021, China)

A Darboux transformation of the coupled Burgers equation is constructed with the help of the gauge transformation of the associated 3×3 matrix spectral problems, from which we obtain some exact solutions of the coupled Burgers equation.

coupled Burgers equation; gauge transformation; Darboux transformation; exact solutions

10.11830/ISSN.1000-5013.201704026

2016-11-22

吴丽华(1983-)，女，副教授，博士，主要从事孤立子与可积系统的研究.E-mail:wulihua@hqu.edu.cn.

国家自然科学基金资助项目(11401230)； 福建省高校杰出青年科研人才培育计划项目(2015年度)； 华侨大学中青年教师科技创新资助计划(ZQN-PY301)

O 175

A

1000-5013(2017)04-0585-06